汤姆逊实验

原子物理

---

在历史上“波动”和“粒子”是两个相互竞争的图像，比如19世纪末，标准的科学问题是“阴极射线是一种粒子还是一种波动？”

在这类争论中，科学家们就像是在搞选举，分裂为两个阵营，以对阴极射线的争论为例，大多数德国科学家认为阴极射线是波动，而大多数英国科学家则认为阴极射线是粒子。

双方都拼命找有利于自己的证据，比如有人用集电器（法拉第笼）收集阴极射线，发现阴极射线是带负电的，由此猜测阴极射线是一种带负电的微小粒子（电的“原子”）。

对立的阵营于是就给阴极射线管加上磁场，然后论证说如果阴极射线是个粒子的话，那它应该在磁场中发生偏转，但阴极射线却没有偏转。这是波动说给粒子说的一个强有力的阻击，但显然没发生波普尔所说的证伪。

这里存在着一个问题，即实验也是可以改进的，否定性结论也和实验的方案、实验的精度有关。比如阴极射线在磁场中是应该发生偏转的，但由于实验条件的限制，比如真空度，比如磁场的绝对强度等等，德国科学家就是没有发现阴极射线能够在磁场中发生偏转。可以想象德国科学家做出了这个否定性结果很Happy，因为缺乏对粒子说的信仰，他们没有进一步改进实验的动力。

回到当时的历史情境，主张波动说意味着你必须把阴极射线看做是某种符合电磁辐射方程的电磁场，你能够通过计算解释实验中的主要现象，又或者你能够证明把阴极射线看做是一种带电粒子，将完全不能解释实验现象，或将导致与实验相反的结论。

电磁波还是带电粒子？这意味着两套方程，两种数学操作的手续，它们吃进一些数据，然后再吐出一些数据，吃进的数据是由实验来的，而吐出的数据也是要和实验比照的。如果我们采用了一套手续，就意味着我没法同时采用另一套手续。

我们讲“波动和粒子是两幅不相容的图像”，我们的意思是：它们是互相竞争、互相替代的两种理论近似（Approach）。而这两种近似又确实是以“波”和“粒子”两种图像为核心构建的。

所谓波就是充盈于整个空间的某种（物理）量的分布，比如电场和磁场，我们可以直接测空间中电场和磁场的强度，电场和磁场的强度又对应能量，因为电磁场是充盈于整个空间的，我们可以在想象中划定一块体积，能量正比于体积，单位体积电磁场的能量就是电磁场的能量密度：

$$\rho(\omega) = \frac{\epsilon_0 E^2(\omega)}{2} + \frac{B^2(\omega)}{2 \mu_0}$$

这里我们把电磁场的能量密度$\rho(\omega)$表示为和频率($\omega$)有关的形式，我们在想象中对电磁场进行分类，按照不同振动的频率分类，然后再把它们加起来。

所谓粒子，就是集中地携带一份动量和能量，假如不考虑相对论的话，能量可以写为：$T + V$，动量可以写为：$p = mv$。粒子的运动满足牛顿方程。

比如带电粒子在磁场中运动，它会受到洛伦兹力$F$的影响，洛伦兹力的大小是$q v B$，这里$q$是带电粒子携带的电量，$v$是带电粒子运动的速度，$B$是磁场强度。洛伦兹力与带电粒子运动的方向垂直，如果粒子带正电的话，粒子速度$\vec v$，磁场$\vec B$和洛伦兹力$\vec F$正好构成一个右手法则

$$\vec F = q \vec v \times \vec B$$

否则，如果粒子带负电，将构成一个左手法则。

引力是非常弱的，我们总可以忽略，在粒子图像下，我们就是要对粒子的受力进行分析，然后求解牛顿方程。而现在力的方向和运动的方向垂直，这符合做匀速圆周运动的条件。假设粒子做匀速圆周运动，其加速度是：

$$a = \frac{v^2 }{R }$$

而向心力就是：

$$m \frac{v^2}{R} = q v B$$

即洛伦兹力正好提供了这个向心力。解出半径$R$：

$$R = \frac{mv}{qB}$$

如果磁场不够强的话，半径$R$会很大，带电粒子以半径$R$做圆周运动，如果我们只跟踪粒子有限距离的话，粒子因洛伦兹力而导致的偏转是很小很小的。

真空技术和磁场是制约实验的主要因素，“真空”是对密闭的管子反复抽气制备的，这首先不是严格的真空，其次如果真空管越细小的话，成本会比较低。同样，基于成本的考虑，磁场强度也不会无限制地大。这是为什么德国科学家没有观察到阴极射线在磁场中偏转的原因。

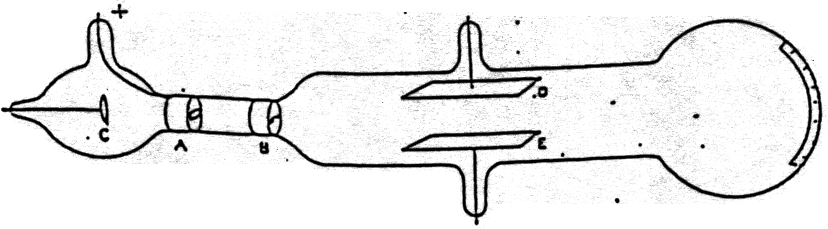
现在需要一位信仰粒子说，坚持理想的人来拯救粒子。这是通过精巧地设计实验达成的。设计实验的人叫J. J. 汤姆逊，虽然是卡文迪什实验室的主任，但当时实验室的经费很少，J. J. 汤姆逊也用不起大磁铁，磁场比较弱，磁场区域比较小⋯⋯，这就是实验的基本限制。

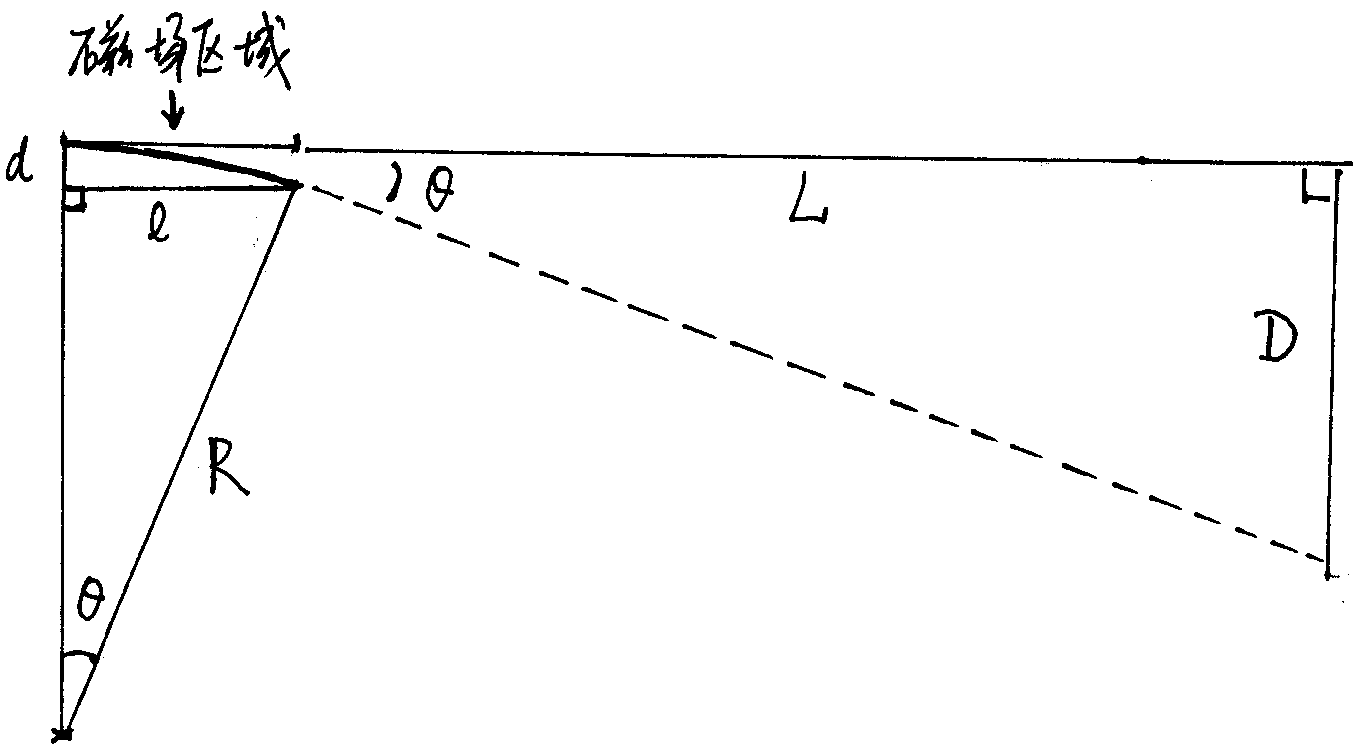
J. J. 汤姆逊的方案是把阴极射线放出来，在经历了一个磁场区域后，再让它自由地飞一段，飞一段比较长的距离，这样偏转就会被放大。假设偏转角是$\theta$，阴极射线在水平方向上飞了距离$L$，最终在竖直方向的偏转是$D$，那么$D \approx L \theta$，即$L$越长，我们就越容易观察到偏转。

阴极射线发生偏转是因为它曾在磁场区域中运行过一段距离，假设这个距离是$l$，在这段距离里阴极射线会因磁场的存在，因洛伦兹力而偏转，偏转角度$\theta$满足如下关系：

$$R \sin \theta \approx R \theta = l$$

阴极射线在磁场里运行的时候也会有个偏转，记为$d$，这个偏转很小，很难被直接测量。但假如有这个$d$的话，线段$R - d$，$l$，$R$将构成一个直角三角形，因此有关系：

$$(R-d)^2 + l^2 = R^2$$

化简后，可以求出：$R = \frac{l^2}{2 d}$，于是$\sin \theta$可以表示为：

$$\sin \theta = \frac{l}{R} = \frac{2d}{l}$$

由于$\theta$很小，$\theta \approx \frac{2 d}{l}$。代入$D \approx L \theta$，$D \approx L \frac{2d}{l}$，求出：

$$d = \frac{D l}{2 L}$$

因此：

$$R = \frac{L l }{D }$$

我们可以代入当年J. J. 汤姆逊的数据来说明这个实验会碰到的困难。

在磁场区域中阴极射线飞了$l = 0.05$米，飞出磁场后阴极射线又继续飞了$L = 1.1$米，最终阴极射线在竖直方向上偏转了$D = 0.07$米。

由此我们可以估算：$d = \frac{ 0.07 \times 0.05 }{ 2 \times 1.1} = 0.0015$米，即1.5毫米，确实很小，考虑到阴极射线本身撞在玻璃上会形成一个有限大小的光斑，这个偏转实际上是无法被测量的。

阴极射线在磁场中运动的半径是：$R = \frac{ 1.1 \times 0.05 }{ 0.07 } \approx 0.79$米，即将近1米，相比于$l = 0.05$米（5厘米）或$D = 0.07$米（7厘米），确实很小。

但现在还有速度$v$不知道，如果假设阴极射线是个粒子的话，那它就可以以一个有限的速度$v$运动，为了把这个$v$表示出来，J J又使用了一个技巧，即加上一个竖直方向的电场，使带电粒子受一个与洛伦兹力正好相反的静电力，这时两个力就抵消了，偏转$D$将归零。

列出力的平衡方程：

$$q E = q v B$$

因此：

$$v = \frac{E}{B}$$

我们还是用J. J. 汤姆逊当年的数据，电场强度$E = 1.0 \times 10^4$牛/库，$B = 3.6 \times 10^{-4}$ 牛/安·米。

求出$v \approx 2.78 \times 10^7$米/秒，将将是光速的十分之一，我们这里忽略相对论效应是安全的。

最终我们可求出：

$$\frac{m }{q } = \frac{B^2}{ E } \cdot \frac{L l }{D}$$

代入J. J. 汤姆逊当年的数据，我们求出：

$$\frac{m }{q } \approx 1.0 \times 10^{-11} kg/C$$

这个比值叫质量电荷比（Mass-to-charge ratio），但现在我们多用其倒数，即电荷质量比（charge-to-mass ratio），2010年CODATA推荐的数值是：

$$\frac{e}{m_e} = (1.758820088 \pm 39) \times 10^{11} C/kg$$

J J 汤姆逊的实验是对粒子说的一大推动，自此之后大家就都倾向于认为在物质中存在着带负电的基本单元——电子（electron），我们把电子的质量记为$m_e$，把电子的电荷记为$e$（但我们需要记住电子所带电荷为负）

Reference

• 温伯格，《亚原子粒子的发现》

• Wikipedia: J. J. Thomson