月亮在没人看时存在吗？实在性和量子理论

量子力学

---

N. David Mermin: Is the moon there when nobody looks? Reality and the quantum theory

译自：Physics Today/April 1985 Page. 38-47

“月亮在没人看时存在吗？”曾广泛地被哲学家们引用，这句出自爱因斯坦口中的名言是有其物理学背景的。在量子力学中客观实在性如何定义看上去是个形而上学问题，但爱因斯坦成功地把这种哲学式的思辩转换为量子力学语言，逼迫我们或者承认量子力学对客观实在的描述是不完备的，或者承认存在神秘的瞬时超距作用。而贝尔不等式及相关实验则帮助我们在这两者之间作出了判断，即看来真的存在幽灵般的超距作用。虽然看起来爱因斯坦的直觉与实验冲突。但正是爱因斯坦对量子力学与实在性的追问揭示出量子力学是非定域的，并且这也开创了关于量子信息学的研究。

爱因斯坦声称对量子理论的形而上学解释需要神秘的超距作用；现在实验告诉我们值得争论的问题已不再是爱因斯坦的困惑，而是真实世界被观察到的行为方式。

作者：N. David Mermin

[David Mermin是康奈尔大学原子与固体物理实验室主任。他是一位理论固体物理学家，最近他提出了关于准晶的一些准思考。对今日物理（Physics Today）的读者来说是他发明了全世界都认同的科学词汇“怖侏”（boojum）。他正在和N. W. Ashcroft一起开始更新那本全世界最棒的固体物理教材。他告诉我们他被贝尔定理困扰，但他的脑子里可能还有石头。]

量子力学是魔术。【1】

1935年5月，爱因斯坦，波多斯基和罗森发表了一篇文章称量子力学未提供对物理实在的完全描述。【2】

50年后的今天，EPR的文章及由此引发的理论和实验工作仍是量子理论为我们揭示出的世界最怪异的方面的生动写照，而使我们印象深刻。当爱因斯坦宣称“上帝不掷骰子”时，他善说警句的天才反而帮了倒忙。因为自此他反对量子力学的根本目标就变成了——“对世界的根本认识只能是几率的”。

但EPR文章，他最有力攻击的是量子学说完全不同的方面：物理性质一般地不再是可以独立于观测的客观实体。

正如约丹（Pascual Jordan）指出的【3】:

“观测不仅妨碍了被测对象，而且创造了它……我们强迫（电子）保持确定的位置……我们自己创造了观测的结果。”

约丹的陈述对当代物理学家来说已经是老生常谈了。在此意义下，我们被教导，测量动作对被测量对象的破坏，由于量子行为的存在而不可避免，甚至对那些有经典对应信息（如位置和动量）的测量也同样如此。

爱因斯坦不喜欢这一点。他希望物体不论是否被观测都应具有性质。【4】

“我们经常讨论关于客观实在的概念。我记得一次和爱因斯坦散步时他突然停下来，转向我并问我是否真的相信仅当我看月亮时它才是存在的。”

EPR的文章聪明地描述了一种情况迫使量子理论声称在时空某处B的性质是对与其分离的另一时空A的测量的后果，AB相距如此之远以致于A的测量影响无法以任何已知的动力学机制影响到B。考虑到这些后，爱因斯坦仍坚持A的性质必须绝对地存在。

神秘的超距作用

关于爱因斯坦立场的很多最简单和最直白的陈述可以在他和玻恩的通信中找到。【5】在这本通信集中（读起来有时象纳博科夫的小说），玻恩始终为爱因斯坦不喜欢量子力学的统计特征而痛苦，玻恩反复地失败，在他的通信和他晚期对通信的评论中，玻恩并未领悟到是什么真正使爱因斯坦困惑。爱因斯坦不断努力，也没让自己表达得更清楚。比如，在1948年3月的信件中，他写道：

“B处真正具有的性质应该……不依赖于对另一空间A处任何测量的影响；它也与在A处是否进行了任何测量无关。如果认识到这些，一个人就很难把量子理论的描述当作对物理实在的完全表述。在这种情况下如果有人仍坚持量子理论，他就必须认为B的物理实在会因A处的测量而发生突然的改变。我对物理的直觉强烈地排斥这一点。”

或，可参考1947年3月的通信：

“我不能真正地相信（量子理论）因为它无法与物理学应描绘时空中的实在，摆脱神秘的超距作用这一理念相冲突。”

“神秘的超距作用”指的是我们通过对A进行测量，B处系统的某性质可取确定值。EPR的文章引入了一个可以描述位于A、B处的两个分离的关联粒子的波函数。

在这个特别的双粒子态中，我们可以通过对A处的粒子进行观测（以下测量在可以确定地获得结果的意义下进行）确定位置或者动量以知道B处粒子的相应测量值。如果B处的实在不依赖于对A的测量，那么B处的粒子必须一直具有确定的位置和确定的动量。

由于量子理论本质地不允许同时获得这些测量值，它一定是提供了对物理实在的一种不完全描述。当然除非，有人声称神秘的超距作用是存在的，即可通过测量A的位置（或动量）然后立刻可或得B的位置（或动量）。

在此戏剧性的时刻泡利在玻恩-爱因斯坦的通信中登场了，1954年泡利从普林斯顿给玻恩写信，泡利在信中尽显其著名的机智。

“爱因斯坦把你的手稿交给我阅读；他并无惹怒你的意思，仅仅说你是一个听不进话的人。这与我迄今形成的印象一致， 我无法从你的信件或手稿里了解爱因斯坦（的观点）。看来你为自己树立了一些愚蠢的爱因斯坦，然后又夸张地把它们击倒。特别地，爱因斯坦并未将决定论这一概念放在它通常所处的根本位置上（正象他多次向我强调的那样）……同时，他也怀疑：是否严格地决定？这一问题是否可作为理论可被接受的判据。”

泡利继续向玻恩陈述爱因斯坦“哲学成见”的真正含义，强调“爱因斯坦的错误是在于‘实在的’而非‘决定的’。”根据泡利，反驳爱因斯坦观点的恰当基础可陈述如下：

“一个人不可能象思考：针尖上能站多少个天使这种古老问题那样去冥思苦想那些他一无所知的事情。但对我来说爱因斯坦的问题总可归结到这类问题上去。”

面对神秘的超距作用，爱因斯坦倾向于相信那些人们不可能知道的东西（比如粒子可同时具有确定的动量和位置）确实是一直存在的。

“那些认为量子力学的描述性方法原则上就是最终形式的物理学家将……放弃对空间中不同部分都独立地存在物理实在性这一要求；而且在量子理论中也没有什么地方必须用到这一要求，这一立场因此得到辩护。我承认这一点，但也要指出：当我考虑我所知的物理现象，特别是那些被量子力学成功地把握的物理现象，我仍然找不到丝毫事实可以表明这一要求是必须被抛弃的。所以我倾向于相信量子力学的描述……必须被认为是对实在的非完备的和非直接的描述……”

新的事实

对“是否在某处存在真实”这一挑战的理论回答是由贝尔（John S. Bell）1964年在一个短命期刊Physics上发表的著名论文上给出的。【6】利用玻姆（David Bohm）提出的理想实验【7】，EPR文章论证所需要的“不可能同时知道的物性”（粒子自旋沿几个不同方向的即时取值），贝尔证明（贝尔不等式）这些性质是不能同时存在的符合量子理论的定量计算。结论则相当程度上与是否相信量子理论提供了对物理实在的完备描述无关。

如果在这样的实验中实验数据符合量子理论的定量预测，那么爱因斯坦的哲学立场就是错的。

在过去的几年中，已经完成了一系列漂亮的实验，巴黎大学理论所和奥斯陆应用光学所的Alain Aspect及其同事【8】通过完成一系列满足贝尔论证所需条件的EPR实验提供了对爱因斯坦挑战的实验回答。

实验表明量子理论所预言的确实被证实了。爱因斯坦发出挑战后的30年，事实——而非形而上学学说——驳倒了他。

（自EPR发表后）对于这50年的思维历史和科学发现的态度是很不同的。【9】玻尔从一开始就理所当然地认真对待它，罗森菲尔德（Leon Rosenfeld）这样描述EPR的影响【10】：

“这个打击对我们来说无疑就是晴天霹雳。它对玻尔的影响是明显的……没有什么比这更糟糕了。乃至玻尔一听完我对爱因斯坦论证的报告，其他一切事情都被放下了。”

贝尔的贡献在也许应称之为准流行的文化中成为著名的。比如，我们可在《跳舞的物理大师》中读到【11】：

“一些物理学家相信这[贝尔定理]也许是物理史上最重要的一项工作。”

确实正如伯克利的理论粒子物理学家Henry Stapp所说【12】：

“贝尔定理是科学史上最深奥的发现。”

另一种声音则认为“晴天霹雳”正是“科学史上最深奥发现”的基础。关于EPR的文章，（物理学家和科学史家）派斯（Abraham Pais）在他最近的关于爱因斯坦的传记中写道【13】：

“我相信，这篇文章最终将只有这部分幸存，是……这句话[‘没有关于实在的合理定义与之相容’]，这句话如此伤心地总结了爱因斯坦晚年对量子力学的态度。”

公平地说，我想大多数物理学家会倾向于派斯的说法而非Stapp，但在大多数近乎漠视和少数极力夸张的立场之间我称之为中庸的态度。这可用以下叙述非常简明地表达，有一次我问一位杰出的普林斯顿物理学家他认为爱因斯坦本人会对贝尔定理做何反应。

他说爱因斯坦会回到家然后努力思考几个星期然后他就无法猜测这时爱因斯坦会说什么了，但无论说什么都将是非常有趣的。他确信爱因斯坦将会被贝尔定理深深地困扰。

然后他补充道：

“不被贝尔定理困扰的人脑袋里一定有石头。”

至此我只能将当代物理学家分为如下两类。

类型1，深深被EPR及贝尔定理困扰的物理学家。

类型2，（大多数）未被困扰，但我们可以把这类再分成两小类。

类型2a，那些解释他们为什么未被困扰的物理学家。他们的解释或者是不着边际的（比如玻尔对爱因斯坦的回应）或者可被证明是包括了错误的物理学断言。

类型2b，未被困扰，也拒绝作出解释的物理学家。他们的立场是无法被攻击的。（还有一种类型2b的变种，他们声称玻尔解决了所有的问题【14】，但拒绝解释是如何做的的。）

一个理想演示

为了测试你属于哪个类型，我将用黑盒子的语言来描述一个简化版本的贝尔理想实验，这种装置工作的机制恰好符合文献中描述的能解释实验数据的量子力学理论分析。可能这种反向的处理方式会使你抛开对量子力学的成见，以全新的态度判断下面我所描述的对你是否足够奇怪【15】。

我脑子里的是一个简单的理想演示。这套装置有三个部件。其中两个（A和B）是探测器。

它们离的很远（在Aspect实验中是超过10米）。每个探测器都有一个开关，可以切换到三个位置中的一个；探测器对事件的反应是或者发出红色闪光或者发出绿色闪光。第三个部件（C），位于AB之间，它起源的作用（图1）。

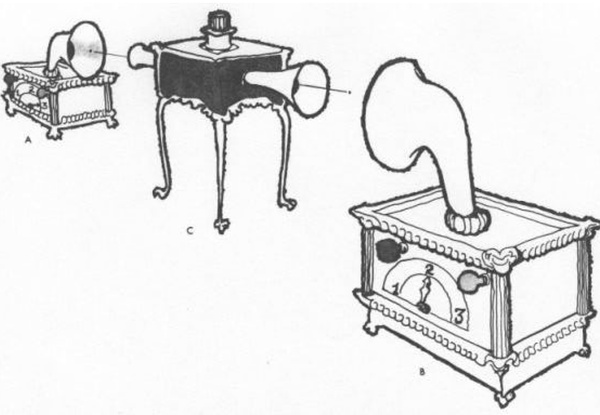
实验装置包括两个探测器，A和B，和一个源C，它可以发出“粒子”或者其他什么东西。实验开始，实验员先按下C的按钮；C向两个探测器发出一些东西。紧接着，每个探测器都会各自发出闪光。在源（C）和其中一个探测器之间放一块砖（障碍物）以阻止探测器发出闪光，然后把探测器移动到离源很远的地方以增加按下按钮和发出闪光之间的时间延迟。探测器上的开关可以随机地由一个跳到另一个。需要声明的是除了由C可以向A和B发出一些东西，实验装置的三个部分之间没有任何联系。

下图是Aspect在法国奥尔赛（Orsay）实现这个实验的实际装置。实验室的中央是真空室，里面的钙原子可以由图中可见的两台激光器激发起来。激发态钙原子发出的光可沿着管道传播6米并被一个双通道偏振器（two-channel polarizer）检测到。

---

实验装置的各部分（ABC）之间没有任何联系，没有机械的联系，没有电磁学的联系，也没有任何已知相关的联系。（我保证一旦你知道黑盒子里的内部情况你就会同意它们之间确实没有联系。）

探测器之间不能互相发信号，也不能以任何已知的机制给源发信号，除非通过C发出的“粒子”源也没法向探测器发信号。演示过程是这样的：

每个探测器的开关都是独立的并随机地拨到它三个位置中的某一个，然后我们按下源上的按钮；紧接着，每个探测器都会闪烁红光（R）或绿光（G）。探测器的开关设置和探测器闪烁光的颜色将被记录下来，然后整个过程会被一次又一次地重复。

记录下来的数据将包括每次实验的一对数字和一对颜色。比如某次实验，对A来说开关拨到位置3，B拨到位置2，A闪烁红光，而B闪烁绿光，实验结果将被记作“32RG”（图2）。

由于在源C和探测器AB之间没有任何内在的联系，在按下源C的按钮和探测器AB发出闪光之间的联系只能是通过源向探测器发出的某种东西，我们叫它们“粒子”，或随便叫它们任何名字。这并不难被检测；比如，我们可以在源和一个探测器之间放上一块砖，在接下来的一轮中，那个探测器就不会发出闪光。当砖块被移走，所有事情将和以前一样。

典型的实验数据如图3所示。

以上数据是从很多很多实验数据中抽取出来的片段，每次实验AB的开关都会随机地变动。（注意黑体的部分）

---

实验数据发现，这里只有两个可以成立的性质：

（I）如果探测器AB的开关放在相同位置，那么它们发出的闪光将是相同颜色的。

（II）如果一个人检测了所有的数据，不管开关是如何设置的，他会发现闪光的颜色是完全随机的。特别地，有一半时间AB将闪烁相同颜色的光，而另外一半时间闪烁不同颜色的光。

以上就是对理想演示的说明。

想一想，你是否对以上数据感到困惑呢？

它是如何工作的？

只考虑探测器开关放在相同位置的情况（图3黑体字部分）。在这种情况下探测器闪烁相同颜色的光。如果它们可以互相通信，这将是一种骗小孩的鬼把戏，AB的开关拨到相同位置，然后AB就闪烁相同的光，但问题是AB之间完全没有联系。它们也不可能按照事先约定好的程序各自发出确定颜色的光，因为当AB的开关设置不同时至少在某些情况下探测器会发出不同颜色的光，而且AB的设置是各自独立的随机选择。

那么，我们应如何解释数据的第一个特性呢？根本没有问题。实际上，玻恩在他1948年5月给爱因斯坦的一封信【5】里提供了一种解释：

“对我来说你的公理‘空间分离的两个独立物体A和B’并不像你所说的那样有说服力。它没有考虑相干性（coherence）这一事实；原来在一起的空间分离的两个物体并不一定是独立的。我相信这是无法否认的而只能接受它。狄拉克的整本书就是以此为基础的。”

在我们的演示里探测器由粒子触发，它们原先就是在一起的，都由源C发出。这样我们就很容易构造出一些对第一条性质的解释。

比如，假设当粒子进到探测器里的时候就相当于是命中了一个靶子，这个靶子被分成八个区域（2的3次方），标记为RRR，RRG，RGR，RGG，GRR，GRG，GGR，和GGG。假设每个探测器都按如下原则工作，当粒子落到GRG区域，如果开关的位置在1它就闪烁绿光（G），如果开关的位置在2它就闪烁红光（R），在3闪烁绿光（G）；RGG导致，在1红光（R），在2和3绿光（G），等等。这样只要假设在每次实验中源发出的粒子总会命中AB的相同区域，我们就很容易解释当AB设置相同时，它们将闪烁相同颜色的光。

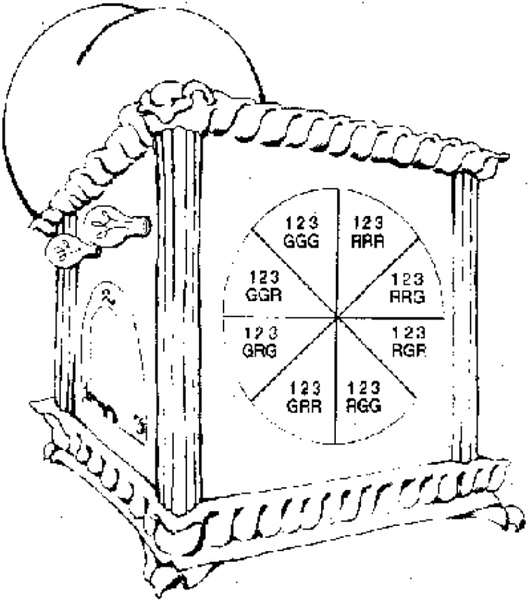
显然这并不是唯一的机制。我们还可以假设粒子有八种形状：立方体，球体，四面体，……

规则如下：

对立方体而言所有的设置都闪烁红光（R），球体在设置1和2下发红光（R），设置3发绿光（G），等等。这样只要假设源每次发出的都是相同形状的粒子，数据的第一条性质就得到了解释。

这些解释的共同特点是要求每个粒子都应当以某种特定方式，携带一系列可以决定探测器如何反应的指令，而且对每次实验而言，射向A和B的粒子都应携带相同的指令：

（I）除了粒子，源（C）和探测器（AB）之间并没有任何通讯，AB设置相同，粒子并不知道设置是11，22，还是33。探测器在设置相同时总闪烁相同颜色的光，粒子携带的指令必须足以让探测器在三种可能的设置下发出确定颜色的光。

（II）由于源和探测器之间缺乏通讯，这要求粒子必须携带对每次实验都足够的指令——甚至也包括AB探测器有不同设置这类情况——因为粒子被发射出来的时候并不知道AB是否处于相同的设置。

对演示的一般解释如下图所示。

为了使探测器在相同设置下发出相同颜色的光，两个粒子必须以某种方式携带足够的指令使探测器知道在每种设置下应闪烁什么颜色的光。每次实验的结果除了实际数据并不反映这些指令是什么；所以，比如对第一个指令（1R）就是“人压根就无法知道的一些东西”，我只是在对它进行猜测，即假设“存在这样的东西”。

---

可惜！这个解释——我坚信，一个人即便没有学过量子力学他也能理解（尽管听上去像是一个有挑战的智力游戏）——是不成立的。

因为它与数据的第二条性质矛盾：这里没有可行的方式去给出这样的指令，使得整个实验，一组接一组的数据，不管探测器的设置为何，整体而言，AB探测器有一半时间闪烁相同颜色的光。

这里我们要停一下以说明“人压根就无法知道的一些东西”——指令集中的第三条——是不能存在的。因为即便指令集确实存在，我们也不可能知道三条（反映在当AB探测器具有不同设置时的那些实验）中的超过两条。讨论如下。

考虑一个特定的指令集，比如，RRG。假设粒子都被赋予指令集RRG，这时探测器在设置11，22，33，12，或21下将闪烁相同颜色的光；在设置13，31，23，或32下将闪烁不同颜色的光。

因为探测器AB的开关位置是独立随机地选取的，这九种设置（3乘以3）的可能性都相等，这样在RRG指令下闪烁相同颜色光的时间将是总时间的5/9。

显然这个结论对指令RGR，GRR，GGR，GRG和RGG也成立，因为这里的讨论只涉及指令集中一个颜色出现两次而另一颜色出现一次这一事实。所有六个这样的指令集都对应闪烁相同颜色光的时间是总时间的5/9。

剩下的指令集是RRR和GGG，对这两种情况探测器将总闪烁相同颜色的光。

所以如果指令集真的存在的话，不管具体的指令集在不同的实验中是如何分布的，闪烁相同颜色的次数将至少是总实验次数的5/9。

这就是贝尔定理（也被称作是贝尔不等式）对这个理想演示所要求的。

但在实际的理想演示中相同颜色出现的时间是1/2。

以上给出的数据违背了贝尔不等式，所以不可能存在这样的指令集。

如果你不知道这里的诀窍是什么，我强烈建议你在阅读量子力学对这一现象的解释之前，自己试着提出一些其他可能的不引入ABC之间联系的对实验数据的第一条性质的解释，然后证明这些解释将和第二条性质矛盾。

一种实现的方式

下面介绍一种可能的对这种理想演示的实现：

让源产生两个自旋1/2的粒子，构成一个自旋单态（spin singlet），分别向两个空间分离的探测器飞去（当然，做到这个并不容易，在下述奥尔赛的实验中，他们用两个关联的光子达到同样的效果）。

每个探测器都包含一个斯特恩-盖拉赫磁铁（其作用是产生沿某个方向的非均匀磁场），它们的取向是$a^{(1)}, a^{(2)}$或$a^{(3)}$，垂直于粒子飞行的方向，并且互相成$120^o$夹角。

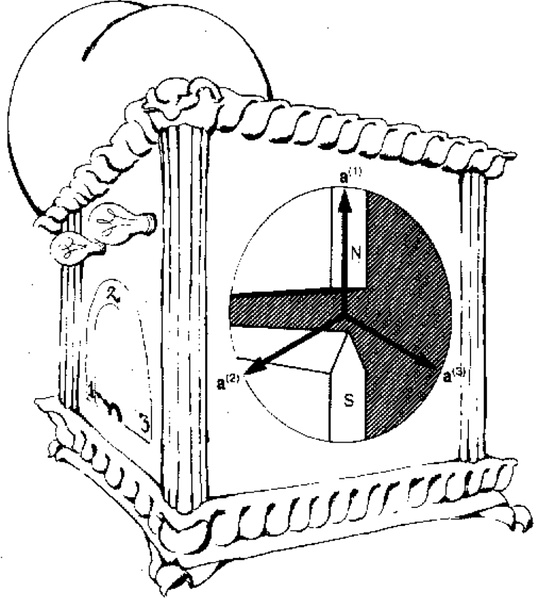
粒子具有磁矩，并且能被探测器里的斯特恩-盖拉赫磁铁分为“自旋向上”和“自旋向下”两类。设置中的1，2，3位置就是使磁铁的北极指向共面单位向量$a^{(1)}, a^{(2)}$, 或$a^{(3)}$中的一个。这三个单位向量之间的夹角是$120^o$，它们的和就是零。两个探测器有相同的开关位置，对应相同方向的磁场。对其中一个探测器，自旋向上，就闪烁红光，自旋向下，就闪烁绿光；对另一个探测器则使用相反的颜色约定。

---

三种开关的设置取决于我们使用哪种磁场取向。一个探测器闪烁红光还是绿光，取决于穿越磁场的粒子的自旋取向是指向磁铁的北极（自旋向上）还是指向磁铁的南极（自旋向下）；另一个探测器则使用相反的颜色约定。

就是这样。很明显在源和探测器之间或两个探测器之间都没有联系。但我们就能解释数据了：

当两个探测器有相同设置时，两个粒子的自旋都延相同方向被测量，所以它们总闪烁相同颜色的光，因为如果测量是延相同方向的话我们总会得到相反的自旋取值。但这是自旋单态结构的直接后果，自旋单态可以表示为：

$$\left| \psi \right\rangle = \frac{1}{\sqrt 2} \left[ \left| +- \right\rangle - \left| -+ \right\rangle \right]$$

自旋单态与自旋量子化轴的取向无关，而且只要两个自旋延任意相同方向测量，“+-”或“-+”有相同的几率，但绝不可能是“++”或“--”。

为了建立对数据的第二个性质的解释，考虑两自旋测量结果的乘积$m_1 m_2$（$m_1, m_2$取值的可能性是$1/2$或$- 1/2$），它将是$-1/4$，对应探测器闪烁相同颜色的光；和$1/4$，对应探测器闪烁不同颜色的光。我们必须说明对所有9种不同的斯特恩-盖拉赫磁场取向对求平均，这个乘积将为0。

对给定的一对取向，$a^{(i)}$和$a^{(j)}$，这个乘积的期望值恰恰是在态$\psi$下对应的（对易）厄米观测量$a^{(i)}\cdot S^{(1)}$和$a^{(j)}\cdot S^{(2)}$的乘积。

这样数据的第二条性质就意味着：

$$\sum\limits_{ij} \left\langle \psi \right| \left[ a^{(i)}\cdot S^{(1)} \right] \left[ a^{(j)}\cdot S^{(2)} \right] \left| \psi \right\rangle = 0$$

上式是量子力学线性性质（linearity）的直接后果，我们可直接对式子里的矩阵元进行求和，三个单位向量构成一个等边三角形，因此它们的和为0：

$$\sum\limits_i a^{(i)} = \sum\limits_j a^{(j)} = 0$$

这就完全解释了数据。也揭开了理想演示的面具，它就是简单改进了的玻姆版本的对EPR实验的实现。如果我们仅在AB相同设置下进行实验，我们将得到精确的玻姆-EPR实验。先前设想存在的指令集在量子力学里就成了胡说八道，因为对不同取向$S \cdot a^{(i)}$，$i = 1,2,3$对应三个不对易的观测量，在测量前它们根本就没有预先的取值。根据EPR，这恰恰来自量子力学形式体系的局限，因为（EPR认为）存在指令集是解释数据第一条性质的唯一方式。

贝尔的分析讨论了AB有不同设置的情况，他根据量子力学推出了实验数据应具有的第二条性质，并且说明了这条性质和根据第一条性质得到的指令集假设是矛盾的，贝尔的分析独立于解释数据所用的形式，也相当独立于任何量子神学的教条。

Aspect实验

Aspect及其同事在奥尔赛的实验证实了量子理论的预言，能够观测到实验结果的条件是能实现的（我的一个杰出的同事一次告诉我说EPR佯谬的答案是自旋单态的关联，但它不可能在宏观尺度上被保持——任何东西，甚至是隔壁屋子的宇宙射线都足以破坏这种效应）。

在这些实验里两个自旋1/2的粒子被一对光子替代，而自旋测量则变成偏振测量。

光子对由被激光泵浦到辐射雪崩（radiative cascade）状态的钙原子发出。因为原子的初态和终态有$J=0$（总角动量为0），量子理论预言（并且实验也证实）如果光子沿相同方向被测量它们将有相同的偏振（用前面理想实验的语言说就是光闪烁相同的颜色）——这就是第一条性质。

但如果偏振在相互交角为$120^o$的方向上被测量，理论预言（而且实验也证实）它们将只有四分之一的时间相同（$1/4 = \cos^2 120^o$）。

这正是产生理想演示第二条性质所需的：假设AB设置是随机的，有1/3的几率设置相同，这样在所有的实验中闪烁相同光的时间将是：

$$\frac{1}{3} \times 1 + \frac{2}{3} \times \frac{1}{4} = \frac{1}{2}$$

奥尔赛的科学家们对某种修改过的贝尔理论感兴趣，他们最感兴趣的交角将是$22.5^o$的整数倍，但他们从很多不同的角度采集数据，并且，除了EPR的专家，这两类实验在概念上的差别很小。【16】

这些实验有一些惊人的结论。两个检偏器被放到间距有13米远而实验结果并没有本质变化，这样就排除了效应会随着AB距离的增加至宏观尺度而逐渐减少的奇怪量子关联（strange quantum correlations）的漏洞（loophole）。在这样的距离很难设想对光子1号的极化测量能够，以任何一般的意义，会“扰动”光子2号。

确实，这样大的距离，假设一个光子在穿越检偏器的时候会产生对另一个光子的扰动，并改变对第二个光子偏振测量的结果，那么这种扰动必须是以超光速传播的。

在奥尔赛小组系列工作的第三篇文章中，古怪的共谋理论（bizarre conspiracy theories）通过一种可以迅速切换每个光子偏振测量方向的天才设计所处理。

每个光子穿过能存在超声驻波的一定体积的水到达检测器。取决于水波的瞬时幅度，光子或者以一种取向直接进入检偏器或者被布拉格反射（Bragg reflected）以另一种方向进入另一个检偏器。

这里驻波决定了检偏器取向的选择，驱动这种选择的声波的频率是如此之高以至于当光由一个探测器飞到另一个探测器的时间里它都可以切换好几次。（这对应一个对理想演示的改进，为了确保严谨，探测器的开关是在粒子从它们共同的源发出之后才随机设置的。）

这意味着什么？

我们应如何理解所有这些呢？这里有没有所谓“神秘的超距作用”呢？

几年前我收到一封从加州某智库执行总监发给国防研究与工程局副局长的信，信里提醒他要注意EPR关联：

“如果我们实际上可以控制超光速非局域效应，就有可能……制造出供潜艇舰队使用的无法被窃听也无法被干扰的高比特指令-通讯系统。重要的是在这个系统里没有一般的电磁信号编码器和解码器，这样也就没什么可以被敌人窃听和干扰的了。敌人将不得不通过实际拥有这个“黑盒子”解码器以截获信息，它的可靠性将不依赖于与编码器的分离或大洋或天气条件……”

真令人兴奋！但这个非定域效应究竟是什么呢？用理想演示的语言说，让我们来谈谈一个粒子的“N-颜色”，N可以是1，2，或3，颜色是当粒子穿过检测器开关设置为N时闪光的颜色，可以是红或绿。

由于指令集不可能存在，我们知道一个粒子不能同时携带确定的“1-颜色，2-颜色和3-颜色”这样的信息到探测器。另一方面，对任意给定N（比如说3），当我们设法先测量了到达B探测器的粒子的“3-颜色”，我们就能在另一粒子到达探测器A之前确定它的“3-颜色”。

假如B处粒子的“3-颜色”是红色，A处粒子的“3-颜色”也将是红色，而当B是绿色时意味着A也将是绿色。

现在有三个问题：

（I）A处粒子的“3-颜色”是否在测量B处粒子的“3-颜色”前就存在？答案不可能是肯定的，因为，在测量B处粒子的“3-颜色”之前，我们有可能会一时兴起随机地选择测量“2-颜色”或“1-颜色”。除非偏执狂，（我们承认）“在B处测量3-颜色前”和“在B处测量2-颜色或1-颜色前”是无法区分的。如果3-颜色已经存在，那么2-颜色和1-颜色也必须存在。但指令集（包含1-颜色，2-颜色，和3-颜色的详情）是不可能存在的。

（II）如果粒子在B处的3-颜色是红色的那么粒子在A处的3-颜色也是红色的吗？答案显然是肯定的，因为在这些情况下总是一个粒子使得A处的探测器闪烁红光。

（III）作为B处测量的后果，是不是有什么（3-颜色的取值）被传递到A处的粒子？

我相信正统的量子形而上学家，将会说“不”，B处的测量不会导致A处有任何改变；改变的是我们对A处粒子的知识。（更加诡异的是，他们可能会反对“在A处”和“在B处”这类短语所暗示的经典质朴的“定域性”或“可分离性”假设）。

这看起来非常明智、非常有说服力：N-颜色根本就不能定义粒子，它仅仅是关于粒子我们知道的。但当我们把“粒子”换成“光子”而“N-颜色”换成“偏振”时，这最后一句还成立吗？并且它真的能帮助你理解为什么当开关设置相同时探测器总闪烁相同颜色吗？

清楚的是这里存在着神秘的超距作用，那么，就像其他幽灵，除了效应本身它压根就无用，不管你在心里是否乞求它。

不论B处的开关设置是什么，单看A处闪烁的红光和绿光，其样式是完全随机的。不管到达A处的粒子有确定的3-颜色（因为B处的开关放在3档）或确定的2-颜色（因为B处的开关固定在2档）或压根没颜色（因为在B处探测器的前面放了一块砖），所有这些都不会对A处颜色的统计分布产生影响。这说明这个“超距作用”只有通过比较A处和B处的数据才能体现出来。

这是最令人困惑的事态，尽管建议用EPR关联来取代声呐是错误的，在我看来因忽视或怀疑我们肯定也错失了一些东西。

EPR实验是我所知物理现象中最接近魔术的，而魔术是应当被欣赏的。这里是否有值得深思的物理还不清楚。我能找到关于这最后问题的最优雅的答案来自我们时代最伟大的物理学家【17】，他（费曼）对这个事情的看法恕我冒昧在本文的最后以诗的形式加以引用：

我们总有很多困难
理解世界的图景
是量子力学给出了它。

至少我确信，
因为我已经足够老了
但我还是没能明白
如何使它对我直白些。

好吧，我仍然被它困扰……

你知道吗它一直就是如此，
每一个新想法，
都要花一代或者两代人
才能显得直白
这样就没有真正的问题了。

我无法定义真正的问题，

所以我怀疑压根就没有真正的问题，
但我还不确定
有没有真正的问题。

没人能在爱因斯坦，波多斯基和罗森之后比这更好地说清它。

参考：

1. Daniel Greenberger, discussion remarks at the Symposium on Fundamental Questions in Quantum Mechanics, SUNY, Albany, April 1984.

2. A.Einstein, B.Podolsky, N.Rosen, Phys. Rev. 47, 777 (1935).

3. Quoted by M. Jammer, The Philosophy of Quantum Mechanics, Wiley, New York (1974) p.151.

4. A.Pais, Rev. Mod. Phys. 51, 863 (1979).

5. The Born-Einstein Letters, with comments by M.Born, Walker, New York (1971).

6. J.S.Bell, Physics 1, 195 (1964).

7. D.Bohm, Quantum Theory, Prentice-Hall, Englewood Cliffs, N.J. (1951) pp. 614-619.

8. A.Aspect, P.Grangier, G.Roger, Phys. Rev. Lett. 47, 460 (1981). A.Aspect, P.Grangier, G.Roger, Phys. Rev. Lett. 49, 91 (1982). A.Aspect, J.Dalibard, G.Roger, Phys. Rev. Lett. 49, 1804 (1982).

9. For a discussion of the views of today’s physicists toward the meaning of the quantum theory, see the interesting and provocative essay “Cognitive Repression in Contemporary Physics” by E.F.Keller, Am. J. Phiys. 47, 718 (1977).

10. L.Rosenfeld in Niels Bohr, His Life and Work as Seen by His Friends and Colleagues, S.Rozental ed., North Holland, Amsterdam (1967) pp. 114-36.

11. G.Zukav, The Dancing Wu-Li Masters –An Overview of the New Physics, Morrow, New York (1979) p.282. On the same page it is also said that “Bell’s theorem is a mathematical construct which as such is indecipherable to the non-mathematician”, a view that I hope the rest of this article will dispel.

12. H.Stapp, Nuovo Cimento 40B, 191 (1977).

13. A.Pais, “Subtle is the Lord…” The Science and the Life of Albert Einstein, Oxford U.P., New York (1982) p.456.

14. N.Bohr, Phys. Rev. 48, 696(1935)

15. 这里所描述的是我从前文章Am.J.Phys. 49, 940(1981)的完善，也考虑了由Richard Friedberg建议的一些改进。其他基本处理可参看贝尔的漂亮文章，“Bertlemann's Socks and the Nature of Reality”, J.Phys.(Paris) 42, C2-41(1981)，和B.d'Espagnat在科学美国人发表的文章和他的书, In Search Reality（寻找实在）, Springer-Verlag, New York(1983)

16. 更多试图实现EPR实验的综述，和各种基于最初贝尔论证发展起来的对种种实验努力的解释，参考 J.F.Clauser, A.Shimony, Repts. Prog. Phys. 41, 1881(1978).

17. R.P.Feynman, Int. J. Theor. Phys. 21, 471(1982).

季燕江 译
译者微博微信: @ianwest