原子物理习题

习题

---

卢瑟福散射

• 质量为$m_1$的入射粒子被质量为$m_2$（$m_2 \le m_1$）的静止靶核弹性散射，证明：入射粒子在实验室坐标系中最大可能偏转角$\theta_L$由下式决定：$\sin \theta_L =\frac{m_2}{m_1}$。

解法(1)：

杨福家书曾推出实验室坐标系下散射公式：

$$\sigma_L (\theta_L ) = ...\frac{...}{\sqrt{ 1- \left( \frac{m_1}{m_2} \sin \theta_L \right)^2 }}$$

若要想让上式有意义，必须满足

$$1 \ge \left( \frac{m_1}{m_2} \sin \theta_L \right)^2$$

这意味着: $m_1 \sin \theta_L \le m_2$，即: $\sin \theta_L \le \frac{m_2}{m_1}$

最大偏转角由下式决定：

$$\sin \theta_L =\frac{m_2}{m_1}$$

QED

解法(2):

$m_1$入射，速度$v$，$m_2$静止，碰撞后，粒子1散射角$\theta$，速度$v_1$，碰撞后粒子2散射角$\phi$，速度$v_2$（如下图）。

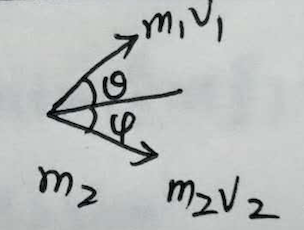
能量守恒

$$\begin{equation}\label{energy} \frac{m_1 v^2}{2} = \frac{m_1 v_1^2}{2} + \frac{m_2 v_2^2}{2} \end{equation}$$

水平方向上的动量守恒

$$\begin{equation}\label{parallel} m_1 v = m_1 v_1 \cos \theta + m_2 v_2 \cos \phi \end{equation}$$

垂直方向上的动量守恒

$$\begin{equation}\label{vertic} 0 = m_1 v_1 \sin \theta - m_2 v_2 \sin \phi \end{equation}$$

[$\ref{parallel}$]$\times \sin \theta$ - [$\ref{vertic}$]$\times \cos \theta$:

$$m_1 v \sin \theta = m_2 v_2 \sin \theta \cos \phi + m_2 v_2 \cos \theta \sin \phi$$

即：

$$m_1 v \sin\theta = m_2 v_2 \sin(\theta + \phi)$$

[$\ref{parallel}$]$\times \sin \phi$ + [$\ref{vertic}$]$\times \cos \phi$:

$$m_1 v \sin \phi = m_1 v_1 \sin (\theta + \phi )$$

即：$v \sin \phi = v_1 \sin (\theta + \phi )$

现在有：

$$v_1 = \frac{ \sin \phi }{\sin (\theta + \phi )} \cdot v$$

$$v_2 = \frac{m_1 }{m_2} \cdot \frac{\sin \theta }{\sin (\theta + \phi) }\cdot v$$

把$v_1$, $v_2$代入能量守恒的表达式[$\ref{energy}$]

$$m_1 v^2 = m_1 \frac{\sin^2 \phi}{\sin^2 (\theta + \phi) } v^2 + m_2 \frac{m_1^2}{m_2^2 } \frac{\sin^2 \theta }{\sin^2 (\theta + \phi)} v^2$$

化简

$$1 = \frac{\sin^2 \phi }{\sin^2 (\theta + \phi) } + \frac{m_1}{m_2} \frac{\sin^2 \theta }{\sin^2(\theta + \phi)}$$

$$\begin{equation}\label{final} \sin^2 (\theta + \phi ) = \sin^2 \phi + \frac{m_1}{m_2} \sin^2 \theta \end{equation}$$

两边分别取微分

$$2 \sin(\theta + \phi) \cos(\theta + \phi) d \theta + 2 \sin(\theta + \phi) \cos(\theta + \phi) d \phi = 2 \sin \phi \cos \phi d \phi + 2 \frac{m_1}{m_2} \sin \theta \cos \theta d \theta$$

$$\sin 2(\theta + \phi) (d \theta + d \phi) = \sin 2 \phi d \phi + \frac{m_1}{m_2} \sin 2 \theta d\theta$$

$$\left( \sin 2(\theta + \phi) - \frac{m_1}{m_2}\sin 2 \theta \right)d \theta =\left( \sin 2 \phi - \sin 2 (\theta + \phi) \right) d \phi$$

$$d \theta = \frac{ \sin 2 \phi - \sin 2(\theta + \phi) }{ ... } d\phi = 0$$

$\theta$取极值时，意味着

$$\sin 2 \phi - \sin 2(\theta + \phi) = 0$$

$$\sin (2 \phi + \theta - \theta ) - \sin(2 \phi + \theta + \theta ) = 0$$

即：$\cos (2 \phi + \theta ) \sin \theta = 0$

这意味着，或者（1）$\sin\theta = 0$，即$\theta = 0$，散射角$\theta$取极值（这里是极小），或者（2）$\cos(2 \phi + \theta) = 0$，即$2 \phi + \theta = \frac{\pi}{2}$，$\theta$取极值。

对第二种情形：

$$\theta = \frac{\pi}{2} - 2 \phi$$

代入公式[$\ref{final}$]

$$\sin^2 (\frac{\pi}{2} - \phi) = \sin^2 \phi + \frac{m_1}{m_2}\sin^2(\frac{\pi}{2} - 2 \phi )$$

即：$\cos^2 \phi = \sin^2 \phi + \frac{m_1}{m_2}\cos^2 2 \phi$

$$\cos 2 \phi = \frac{m_1}{m_2}\cos^2 2 \phi$$

得到：

$$\cos 2 \phi = \frac{m_2}{m_1} = \cos (\frac{\pi}{2} - \theta ) = \sin \theta$$

即$\sin \theta = \frac{m_2}{m_1}$也会导致一个散射角的极值点，这个点对应的是极大值$\sin \theta_L = \frac{m_2}{m_1}$。

QED

简并度

原子在热平衡条件下处于不同能量状态的数目按玻尔兹曼分布($\propto e^{-E/kT}$),

$$\frac{N_2}{N_1} = \frac{g_2}{g_1}e^{-(E_2 - E_1)/kT}$$

$N_1$是微观能量为$E_1$的原子数, $g_2$, $g_1$分别是能态$E_2$和$E_1$的简并度。

考虑到，$E_n$的简并度,

$$2 n^2 =2 \sum\limits_{l = 0}^{n-1} \sum\limits_{m=-l }^l 1 = 2 \left[ 1 + 2(n-1) +1 \right] \frac{n}{2}$$

因此,

$$g_1 = 2$$

$$g_2= 8$$

又，

$$E_n = - \frac{13.6 ev }{n^2}$$

$$E_2 - E_1 = 13.6 \times \frac{3}{4} eV = 10.2 eV$$

考虑氢原子气处于20摄氏度,

$$kT = 8.6 \times 10^{-5 } \times (273 + 20 ) eV = 2.5 \times 10^{-2} eV$$

$$e^{- (E_2 - E_1)/ kT} = e^{- 400 }$$

两边取对数,

$$\lg C = - 400 \lg e = -174$$

$$N_2 = N_1 \frac{8}{2} \times 10^{-174} = 4 N_1 \times 10^{-174}$$

$$N_1 = \frac{N_2}{4} \times 10^{174}$$

$$N_2 = 1$$

$$N_1 = 2.5 \times 10^{173} = \frac{2.5 \times 10^{173}}{6.02 \times 10^{23}} \text{mole} = 4.15 \times 10^{149} \text{mole}$$

1摩尔对应22.4升,

$$V = 90 \times 10^{149} \text{litre}$$

单位换算

• 处在重力场中的中子（neutron），请证明：$m_n g \approx 1.03 \times 10^{-9} eV / cm$，这里$g = 9.8 m \cdot s^{-2}$

解：

$$m_n g =m_n c^2 \cdot \frac{ g}{c^2}$$

$$m_n c^2 = 940 \times 10^6 ev$$

$$\frac{g}{c^2} =\frac{9.8 m s^{-2} }{9 \times 10^{16} m^2 s^{-2} } = 1.09 \times 10^{-16 } m^{-1}$$

$$m_n g \approx 1.02 \times 10^{-9 } eV/cm$$