@jiyanjiang
2015-12-30T04:13:00.000000Z
字数 12841
阅读 3335
自旋的发现
未分类
有两种讲授量子力学的方法,一种是按照历史的逻辑,介绍黑体辐射、关电效应、康普顿散射、卢瑟福散射、玻尔模型、塞曼效应等一系列著名实验,说明经典物理是如何失效的,然后建立“波粒二像性”概念,即“像波一样的粒子”,然后我们用波函数、薛定谔方程来描述电子。
以氢原子为例,不考虑相对论,我们需要求解这样一个偏微分方程:
还有一种讲授量子力学的方法是直接从某一个实验出发引入量子力学。比如费曼就是从假想的双缝实验出发建立量子力学的,讨论双缝实验的好处是方便和费曼发明的路径积分方法对接。除双缝实验外还有一个选择,就是通过讨论斯特恩-盖拉赫实验引入量子力学。
但首先,让我们讨论“磁矩在磁场中运动”。
磁矩在磁场中运动
所谓磁矩就是一个小磁针。假设一个小磁针放到磁场里,磁矩在磁场中不受力,但会受到力矩的作用,它会倾向于倒向和磁场平行的取向。
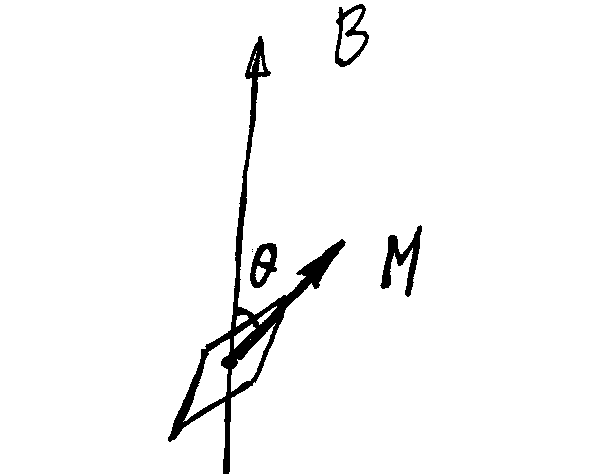
假设磁针的磁矩是,磁场是,其能量为:
类似于陀螺会在重力场中进动,磁矩也会围绕磁场进动。
力矩是:
这里是角动量。
假设这里的磁矩、角动量都是“环形电流”导致的,即假设电子围绕轴做圆周运动导致的磁矩和角动量。
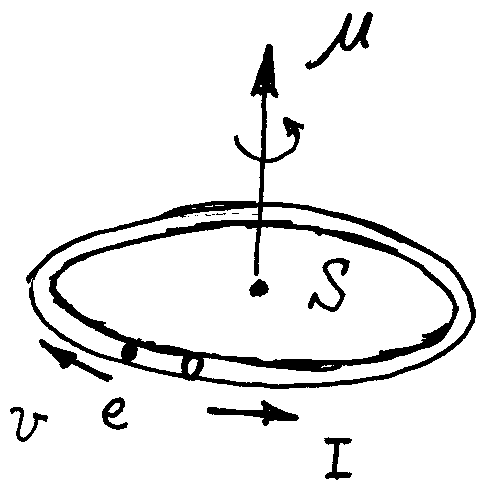
角动量:
磁矩等于电流乘以电流围成的面积,电流是单位时间通过某截面的电荷数,即,如果取电子运行周期是的话,正好是电子的电量(负号表示电子带的电量是负的)。
现在:
换句话说电子的轨道运动会导致电子具有轨道运动的角动量(就像地球围绕太阳运动,地球会具有轨道角动量一样),同时电子是带电的,因此电子的轨道运动也会导致电子具有磁矩,就像一个环形电流会具有磁矩一样,因为都是电子的运动导致的,我们会发现磁矩和角动量是成正比的,我们把这个比例因子进一步改写为:,这里负号表示电子是带负电的,是朗德因子,因为我们很快将发现电子不但具有轨道磁矩,它还将具有自旋磁矩。
字面上理解好像是说电子会同时参与两个运动,就像我们的地球在太阳系里的行为一样,一个是电子因轨道运动(这里就是半径为的匀速圆周运动)导致的磁矩,另一个是电子因自旋运动(字面意思就是电子自己围绕自己旋转)导致的磁矩。对轨道运动而言,对自旋运动而言。写成统一的形式:
我们用表示一般的角动量,用表示轨道角动量,表示自旋角动量,当然马上我们会发现“自旋”(Spin)是个错误的命名。
在原子物理中我们用玻尔磁子(Bohr magneton, )作为磁矩的单位:
斯特恩-盖拉赫实验
我们可以通过讨论斯特恩-盖拉赫实验直接引入量子力学。
斯特恩-盖拉赫实验是个充满了意外的实验,斯特恩(Otto Stern)是爱因斯坦的第一个学生,但他却是个实验物理学家,他想用实验验证当时原子物理研究中的主流理论——“玻尔-索末菲模型”(Bohr-Sommerfeld model)。
玻尔模型是个大杂烩,为了解释原子光谱他把很多并不相容的假设捏在了一起。比如他让电子在一个轨道上围绕原子核运动,这就是经典力学。但他又引入了量子化条件,只允许电子在几个分立的轨道上围绕原子核运动,这就又不要经典力学了。
但既然玻尔模型能够很简单地解释氢原子光谱,而且推导又那么简单,物理学家认为这个对原子现象的描述还是很有潜力的,比如索末菲就对玻尔模型进行了推广。原子中电子和原子核之间符合库伦力,一个平方反比的吸引力,原子核本身的质量比电子质量大很多很多,这些都使得原子就像是一个微小的太阳系,根据开普勒的运动定律行星在一个椭圆轨道上围绕太阳运动,而椭圆是可以有不同偏心率的(圆是一种特殊的椭圆,偏心率为0)。
索末菲把玻尔模型中的圆轨道推广到椭圆轨道,同时他把玻尔的量子化条件也推广了。他引入了两个量子数,一个角量子数,使:
这里是电子在椭圆上运动时的方位角,,是拉氏量。
另一个是径向的量子数,使:
使用极坐标系()描述电子在原子核附近的位置,是矢径,从原子核指向电子,定义为。对正圆运动来说,是个常数,所以是可以等于0的。

玻尔-索末菲模型,这里相当于是
,就是原先玻尔模型中的量子数(主量子数)。
玻尔-索末菲模型:
| 主量子数 | 角量子数 | 磁量子数 | 矢径量子数 |
|---|---|---|---|
| 1 | 1 | 0 | |
| 2 | 2 | 0 | |
| 1 | 1 | ||
| 3 | 3 | 0 | |
| 2 | 1 | ||
| 1 | 2 |
对而言,,只能等于0。这是氢原子能量最低的态,称之为基态。考虑到电子既可以是顺时针围绕原子核运动,也可以是逆时针围绕原子核运动的,于是一个就对应两个“状态”,用角动量的语言说就是,但角动量在方向上的投影只能取两种情况,即角动量的取向也是量子化的,只能沿轴向上或向下。我们把写作,这里,我们管叫做磁量子数,只要不是0,原子就会在方向上有非0的磁矩。
量子化条件会引入不同于经典物理的陈述,比如能量分裂成一个一个能级——能量量子化;现在又导致角动量的分量只能取分立值(对氢原子基态而言是两个),我们称这种现象为空间取向的量子化(Space quantization)。
虽然“玻尔-索末菲模型”能解释不少物理实验,但对这么一个大杂烩式的理论,物理学家并不真的相信。比如电子是否真的会在原子里面按照圆形或椭圆形的轨道运动?这样的图像辅之以量子化条件等也许能够解释实验,但如果电子真的这么行为的话,那也太神奇了。
玻尔-索末菲模型下的“镭”原子:
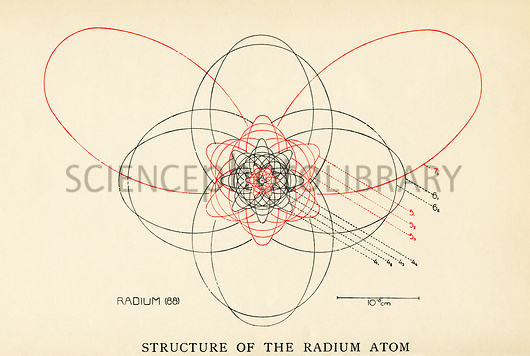
斯特恩是物理化学的博士,但他却有幸成了爱因斯坦的第一个学生,作为犹太人,他的父母坚决资助他们的儿子继续深造。一战结束后,斯特恩又成了玻恩的助手,当时玻恩在法兰克福大学任教并领导一个实验室,在那里斯特恩研究了原子束方法。所谓原子束方法就是用一个炉子给金属加热,使金属原子从炉子里跑出来,通过准直装置后,然后再对射出来的金属原子进行各种操作和测量。
斯特恩知道要想验证氢原子的“空间取向量子化”,就要让的基态氢原子分开,但如何把不同的氢原子分开呢?斯特恩有一天醒早了,当时是冬天,他怕冷于是就躺在被窝里想这个问题。他想到可以让氢原子通过一个在方向上的非均匀磁场,磁场的非均匀性可以通过磁场的梯度来描述,如果梯度足够大的话,就有可能把不同角动量的原子分开。
假设原子的磁矩是,它在磁场中的能量是:
由于磁场是非均匀的,磁矩将会受到一个非0的力:
这里,,分别是和方向上的单位矢量,换句话说,原子受到的力在磁场的非均匀方向上,即方向上,力的大小是:
可见这个实验的难点确实在磁铁上,磁铁的规格要使得越大越好,同时磁铁要足够长,这样不同大小的力会驱动银原子在方向上漂移足够长时间,使具有不同磁矩的原子充分分开。
斯特恩有了这个想法后很兴奋,于是跑去向玻恩汇报,但玻恩并不认为这个实验有价值,在他看来“空间取向量子化”无非是个象征,在它的背后还有我们暂时不懂的物理,而斯特恩竟然在字面上相信会有这么回事,……,这就是他自己的事了[1]。
斯特恩获得了盖拉赫的帮助,而盖拉赫直到此时才第一次听说“空间取向量子化”。实验很难做,花了斯特恩和盖拉赫一年多时间。
他们使用的是银原子Ag,用炉子把银加热到1000多摄氏度,然后使跑出来的银原子通过两个只有0.03毫米宽的准直装置。磁铁有3.5厘米长,磁场强度是大约0.1特斯拉,在方向上的梯度达到了10特斯拉每厘米。银原子确实分裂成了两束,两束的间隔只有0.2毫米,而准直装置或磁铁的方位只要差0.01毫米就会把银原子的分裂图样破坏掉。可想而知这是一个十分精细的实验。


积累在靶上的银原子很少,盖拉赫什么都没看到,他把靶板递给斯特恩,这时他们看到银原子积累的痕迹逐渐显现。很神奇,他们把这归结为银的硫化,因为斯特恩当时的薪水很低,他在实验室里抽劣质的雪茄,他们分析可能是劣质雪茄里的硫太多了,使银硫化,而硫化银是黑色的,很容易被看到。
尽管如此,斯特恩和盖拉赫仍然无法得到稳定的图样,他们的结果在证实和否定“空间取向量子化”之间摇摆。同事们也质疑他们的实验,比如德拜就认为“空间取向量子化”根本就不可能被观察到[2]。
斯特恩和盖拉赫都是挺固执的人,面对质疑盖拉赫说:“在这个世界上没有不值得试的事情。”(No experiment is so dumb, that it should not be tried.)
除此之外,他们还碰到很严峻的财务危机,当时德国正处在一战后的困苦中,玻恩竭尽一切办法为斯特恩-盖拉赫实验筹款。他利用公众对相对论的兴趣在学校最大的演讲厅内为爱因斯坦办系列公共演讲,并对参加的听众收取门票。但通货膨胀太厉害了,靠这笔钱也就支持了几个月。最后还是多亏了美国的银行家Goldman(金人)[3]出手寄了几百美元给玻恩。于是,实验继续。
尽管如此,实验进展得仍不如意。1922年,斯特恩去罗斯托克做教授,他和盖拉赫在哥廷根碰头决定放弃实验。但一次铁路罢工改变了这个实验的命运,当时盖拉赫正坐着火车在回法兰克福的途中,因为罢工他在火车上又把实验的种种细节回顾了一遍,他想到了如何改进准直的新主意,回到法兰克福后他继续实验,这一次他获得了非常清晰的分裂条纹。进一步的计算表明,条纹的分裂确实对应个玻尔磁子()磁矩的区别,误差在10\%左右。
1922年2月13日,盖拉赫给玻尔寄出一张明信片,背后附有实验结果的照片。明信片上说:“尊敬的玻尔先生:附上我们……所得方向量子化的实验证据。我们祝贺您的理论得到证实。”
表面看这是对玻尔-索末菲理论的直接证实,但其实只是巧合。求解氢原子的薛定谔方程,我们可以得到三个量子数:
主量子数:,
角量子数:,
磁量子数:,
氢原子的基态,对应,,,换句话说氢原子的基态应该是没有角动量的,也没有磁矩。当然斯特恩-盖拉赫实验里用的是银原子,银原子正好只剩一个5s电子在最外层,其他电子在内层,其磁矩都相互抵消掉了。对5s电子而言,,,,也没有角动量和磁矩。
那么斯特恩-盖拉赫实验应如何解释呢?实际上它是表明电子具有新角动量——自旋角动量的实验证据。自旋(spin)这个名称来自与经典图像的类别,但这个对比又是不成立的!换句话说这个名字取错了,但名字无非是个指称,物理学家似乎不太在乎这个名字会给门外汉带来误导,他们只是强调自旋是电子(或粒子)的内禀性质,和空间位置()无关,既然和空间位置无关,我们也就无法把自旋想象成一种在三维空间里发生的自己围绕自己的转动了。
仿照玻恩的句式,我们可以这么说:
自旋只是个符号,你要是做字面理解那你可就太Naive了。
连续的斯特恩-盖拉赫实验
自旋不是真实的,但无论如何斯特恩-盖拉赫实验是真实的。我们可以忘掉玻尔-索末菲理论,继续挖掘这个实验的内涵。
我们把具有方向上的非均匀磁场的斯特恩-盖拉赫装置记做,银原子通过后将在方向上分裂为两束。分别对应磁矩为,磁矩是在方向上的,我们称的那束为,的那束为(假设自旋的朗德因子是2,,负号很讨厌,这是因为电子带的是负电)。
非均匀磁场的取向是任意的,如果我们设法使银原子通过一个方向非均匀的磁场,即通过SGx,我们会观察到银原子在方向上的分裂,分裂成对称的两束,对应方向上的磁矩,对应的那束是,对应的那束是。
类似地,我们让银原子通过方向上的非均匀磁场,我们会观察到银原子在方向的分裂,也是对称的两束,我们称对应的那束是,对应的那束是。
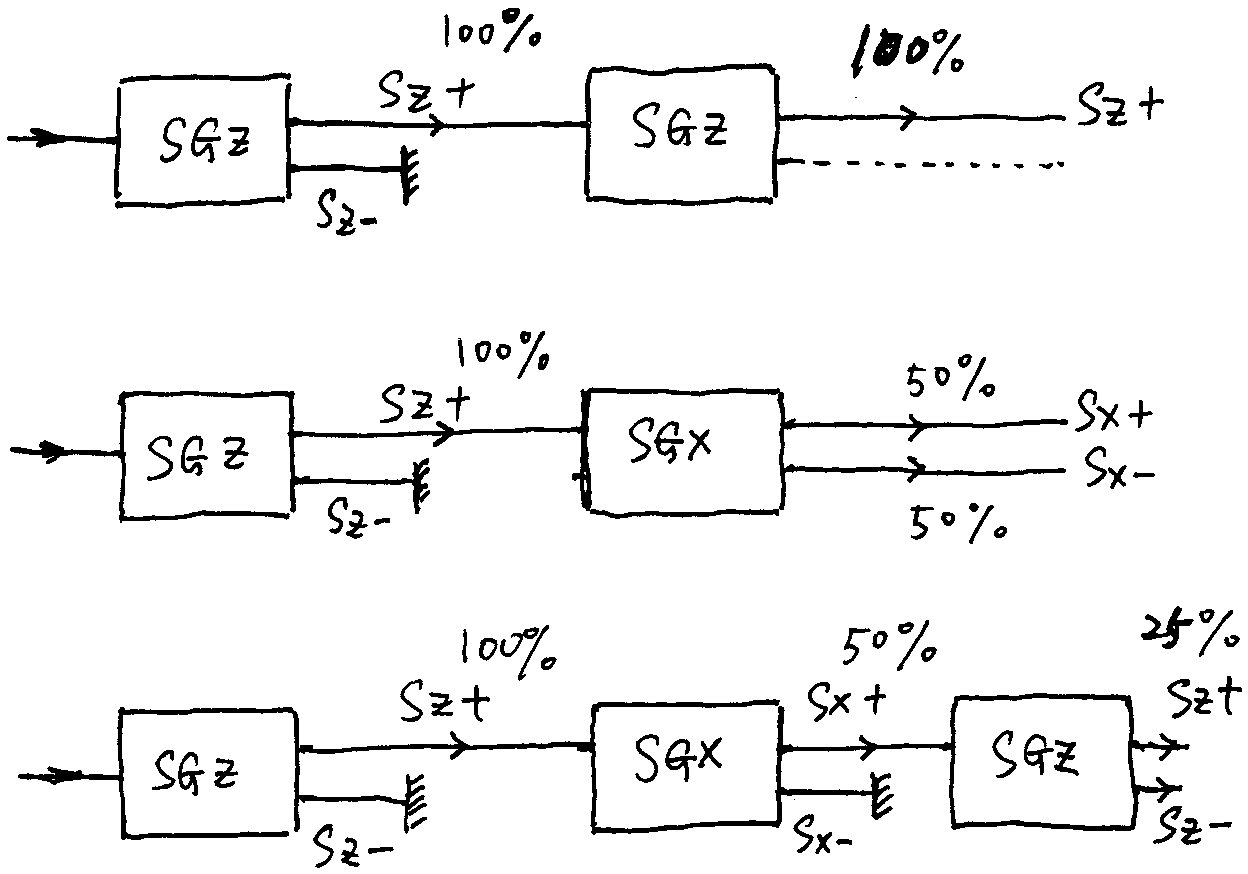
现在我们使这些实验组合起来,比如:
先让银原子通过SGz,银原子分成对称的两束,我们用隔板挡住的那束,只让的那一束出射,这个动作就是一个选择或过滤的动作。好比我们在一个篮子里放了一堆水果,有香蕉也有苹果,我们现在做一个选择,丢掉香蕉,把苹果留下来。
我们把这种专门选择的斯特恩-盖拉赫装置记为SGz+,类似地还有SGz-,专门选择的银原子。类似地我们还可以定义SGx+,SGx-,SGy+和SGy-。
现在我们来做这样的组合实验:
我们现在使用狄拉克的记号,把的银原子用记号表示。我们用表示量子力学的一个态,括号里面放上可以描述这个态的参数,现在就是z+,和银原子束如何在方向上发生偏转有关。
让银原子束先通过SGz+,即把的态选择出来,然后再通过一次SGz+,还是选择,最后出射的还是。
现在考虑组合:
这个组合的作用是先选择,再试图从中选择,实验表明最终没有任何银原子出来。这说明:和是两个不相容的态,里面完全没有,里面完全没有。
这就好像是两个互相垂直的矢量,A向B投影,或B向A投影都是0,我们可以说A里面完全没有B的成分,相反B里面也完全没有A的成分。
同时把任意的态分解为和的线性组合又是完备的,因为我们使银原子通过SGz时只得到了对称的两束,换句话说在这个标准下对银原子分类只能得到两类。
下面我们在SGz+和SGz-之间插入一个SGx+:
方向上的非均匀磁场意味着变换了筛选法则。当然我们还可以推测,比如我们把想象为对水果种类的筛选,而想象为对水果颜色的筛选,那么我们有可能从“红苹果”中找出“香蕉”吗?在这种推测下,我们会认为没有银原子束出射。但最终结果只能实验说了算,实验表明有态的银原子出来。
类似地,我们还可以做这样的实验:
……
它们都会有银原子出来。
我们管这样的实验叫“连续的斯特恩-盖拉赫实验”(sequential Stern-Gerlach experiment)。
现在的问题是如何解释实验。
如果我们认为这样的态存在的话,即存在一个对自旋态(我们从现在开始不说银原子了)的陈述,我们可以同时说而且,那么我们就没法从中筛选出。
为了理解连续的“斯特恩-盖拉赫实验”,我们只有求助于比喻,即用我们熟悉的现象来类比,而建立比喻并不需要两种现象很像或……,所谓比喻是可以任意建立的,比如这里我们可以建立一个“颜色-形状”比喻来理解连续的“斯特恩-盖拉赫实验”。
假想在黑箱里有一堆小物件,我们应如何对其分类呢?比如颜色是一个分类的标准,形状是另一个分类的标准,颜色和形状是完全不相干的描述物件性质的两个标准。
我们说一个小物件是白色的;或是黑色的;白色和黑色是两种互相排斥的陈述,只要是白色的就不能是黑色的,相反只要是黑色的就不能是白色的。
我们也说一个小物件是个立方体,或说它是个球体。球体和立方体也是互相排斥的,我们没法说它既是球体又是立方体。
假设在我们的世界里,这个小物件不是立方体就是球体,但不能既是立方体又是球体。类似的我们说在我们的世界里,这个小物体不是白色的就是黑色的,但不能既是白色的又是黑色的。
形状是我们对物件的陈述,颜色也是我们对物件的陈述。现在我们的问题是:我们能够同时使用颜色和形状来陈述一个物件吗?
在经典世界里,或在我们的日常经验中,当然可以,香蕉是黄色的,同时它也是弯曲的棒棒形,形状和颜色是我们一眼看去可以直观的。
但在量子世界里,这种陈述是被禁止的!看清楚了物件的颜色,物件就完全没有形状;同样看清楚了物件的形状,那它就没有颜色[4]。
这非常反直觉。但需记住,这种叙事是基于比喻建立的,如果我们换一个比喻的话,比如光的偏振现象,我们就会觉得一切都会来的很舒服。(对相同事件,切换视角,任意武断地使用比喻(图像)进行叙事是发现的门径。)
与光偏振现象的类比
我们现在来建立对连续斯特恩-盖拉赫实验的数学描述,考虑:
假设银原子从SGz+出来的比例是100\%,通过SGx+后就只剩下50\%,然后通过SGz-还剩25\%银原子。
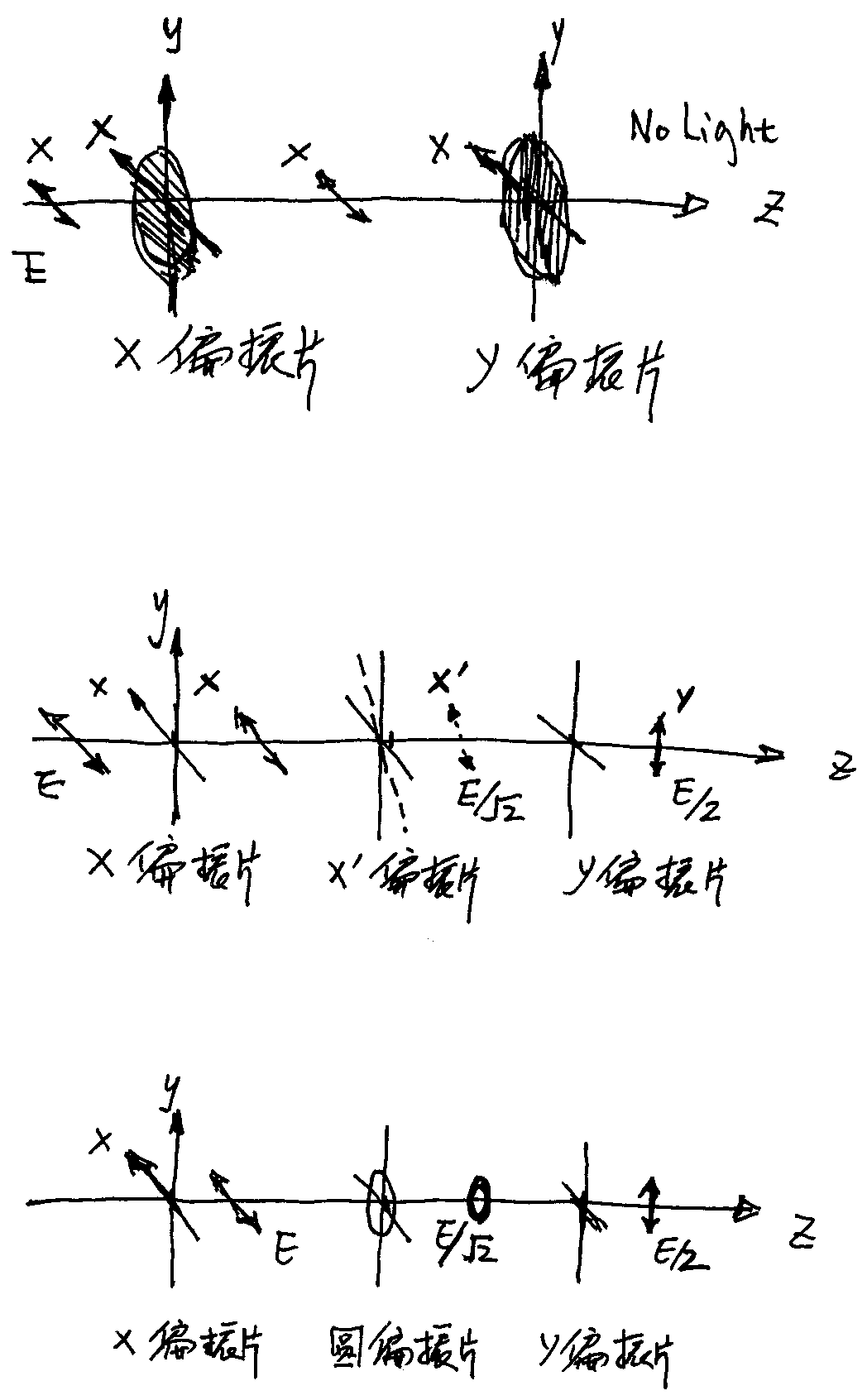
我们可以通过与光偏振现象的类比来建立自旋的理论。光有线偏振光,还有圆偏振光。
比如我们使偏振片的偏振方向与x轴平行,它的作用就是使电矢量垂直于x轴的光统统被吸收,而电矢量平行于x轴的光全部通过。这样我们就得到一个x偏振的光,这也是筛选。
对一束x偏振的光而言,没有任何y偏振的成分,相反亦然,这可以类比态和,它们都是互相排斥的分类标准。
现在使偏振片旋转,我们称之为x'偏振片,它筛选出x'方向的偏振光,继续旋转得到y'偏振片,筛选出y'偏振光,x'和y'是垂直的,因此x'偏振光中不会有任何y'的成分,反之亦然。
并且如果我们让一束光先通过x偏振片再通过x'偏振片,最后通过y偏振片的话,我们会看到出射光,而且百分比和刚才连续的斯特恩-盖拉赫实验的实验结果是一致的。
因此,我们就可以用x'偏振光来类比态,y'偏振光来类比。
但我们还有态和,它们应和什么样的偏振光来类比呢?
我们还有圆偏振光,R右旋光和L左旋光是互相排斥的分类标准,正好可以对应态和。
现在我们的问题就转换为如何描述偏振光了,假设光沿方向传播,光是横波,电矢量只能在平面上振动,因此我们用平面上的一个矢量来表示:

振幅为的x线偏振光先向x'方向投影,振幅变为,最后向y方向投影,振幅变为。光强正比于振幅的平方,因此光强的比为:100% : 50% : 25%。
平面里的任意矢量可以表示为一个二维列向量,如矢量:
我们可以用一个二维的列向量来描述任意一束偏振光,但为了描述圆偏振光,列向量中必须出现纯虚数,换句话说我们是用一个复系数的二维列向量来描述沿方向传播的光的偏振态的。
1.
沿轴传播的x线偏振光可表示为:
沿轴传播的y线偏振光可表示为:
这里分别是轴和轴上的单位向量。我们一般把它们写为列向量的形式,第一行对应分量,第二行对应分量。
再把它们改写为复数的形式。
2.
沿轴传播的x'和y'线偏振光可表示为:
3.
沿轴传播的右旋R圆偏振光和左旋L圆偏振光可表示为:
由于我们把自旋的态类比为光的偏振态,因此我们可以尝试把自旋的态表示为一个复系数二维向量空间中的一个向量。
1.
我们分别用x线偏振光和y线偏振光来表示和。即尝试性地把表示为列向量,把表示为列向量。即:
这里读作“表示为”,以示与“等于”的区分\footnote{等于只用于同类间的关系,而“表示为”或比喻则可用不同类的现象互为引证。}。
2.
态可表示为:
3.
态可表示为:
练习
斯特恩-盖拉赫实验,银原子束从温度为600K的炉子跑出来,经过准直装置后,通过一个0.1米长的非均匀磁场,磁场的梯度是特斯拉/米。银原子从非均匀磁场跑出来后又继续“飞”了1米,求最终银原子在靶上的分裂宽度是多少。(假设银原子的平均速度为,它的平均动能是,这里是银原子的质量,是玻尔兹曼因子。)
[1] “It took me quite a time before I took this idea seriously. I thought always that (space) quantization was a kind of symbolic expression for something which you don’t understand. But to take this literally like Stern did, this was his own idea… I tried too persuade Stern that there was no sense (in it), but then he told me that it was worth a try.” 摘自:“Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics”,Physics Today 56, December 2003。 ↩
[2] “But surely you don’t believe that the (spatial) orientation of atoms is something physically real; that is (only) a timetable for the electrons.” 摘自:“Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics”,Physics Today 56, December 2003 ↩
[3] Goldman是著名投行Goldman Sachs(高盛)的创始人,他虽然是犹太人但对德国比较友好,1930年代初起移居德国。1936年,在大屠杀发生的前夜,Goldman狼狈逃出德国,保住性命,但其在德财产皆被纳粹没收。 ↩
[4] 使用苹果、香蕉的语言:“设想我们先筛选出苹果,然后换个筛选标准,对苹果按颜色筛选,筛选出所有“红色的苹果”,注意!问题就在这里,一旦你说出了“红色的苹果”这一陈述,我们就没法从“红色的苹果”中筛选出香蕉了。”正确的陈述是:“我们首先筛选出苹果,然后换个筛选标准,对苹果按颜色筛选,但这两个标准是相克的,我们一旦知道了颜色,我们就完全丧失形状的信息,现在我们只知道是红色的,但完全不知道到底是苹果和香蕉,最后我们是对红色的水果筛选出香蕉。” ↩
