语言学：为语言的死亡建模

语言学 微分方程

---

Modelling the dynamics of language death, Nature, Vol 424, 12 August 2003

---

这里作者发展了一种简单的语言竞争模型以解释Welsh, Scottish Gaelic, Quechua衰落的历史数据

考虑高度联系的人群，没有空间和社会结构，假设所有的人都只说一种语言。

假设系统包含两个竞争语言X，和Y，语言的吸引力由操此种语言的人口及其地位[1]决定。

假设一个个人由Y转投X的转变几率，每单位时间，是$P_{yx}(x,s)$，这里x是操X语言人占总人口的比例，$s \in [0,1]$描述了X语言的地位。

能描述以上参量的最小模型是：

$$\frac{dx}{dt}=yP_{yx}(x,s) - xP_{xy}(x,s)$$

这里$y = 1-x$，是时刻t操Y语言在总人口中所占的比例。

基于对称性的考虑XY互换应有相同的转换几率。因此，

$$P_{xy}(x,s) = P_{yx}(1-x,1-s)$$

进一步假设如果人口是0，就没有人改说此语言了，

$$P_{yx}(0,s) = 0$$

也没有人改说地位为0的语言，

$$P_{yx}(x,0) = 0$$

并且假设$P_{yx}$是光滑单调的曲线，即随着x和s的增加它是单调增加的。

这意味着微分方程有三个不动点(fixed points)。只有$x=0$和$x=1$是稳定的。

这意味着在该模型下两种语言无法稳定共存。肯定有一种语言要消亡。

作者采集了很多数据，并对数据进行了拟合。

假设转移几率具有幂律的形式。

$$P_{yx}(x,s)= cx^a s$$

$$P_{xy}(x,s)= c(1-x)^a (1-s)$$

作者发现对不同文化中的语言演化现象，

$$a = 1.31 \pm 0.25$$

不同的s是最有意思的，小s将导致语言的快速改宗现象(图b)。

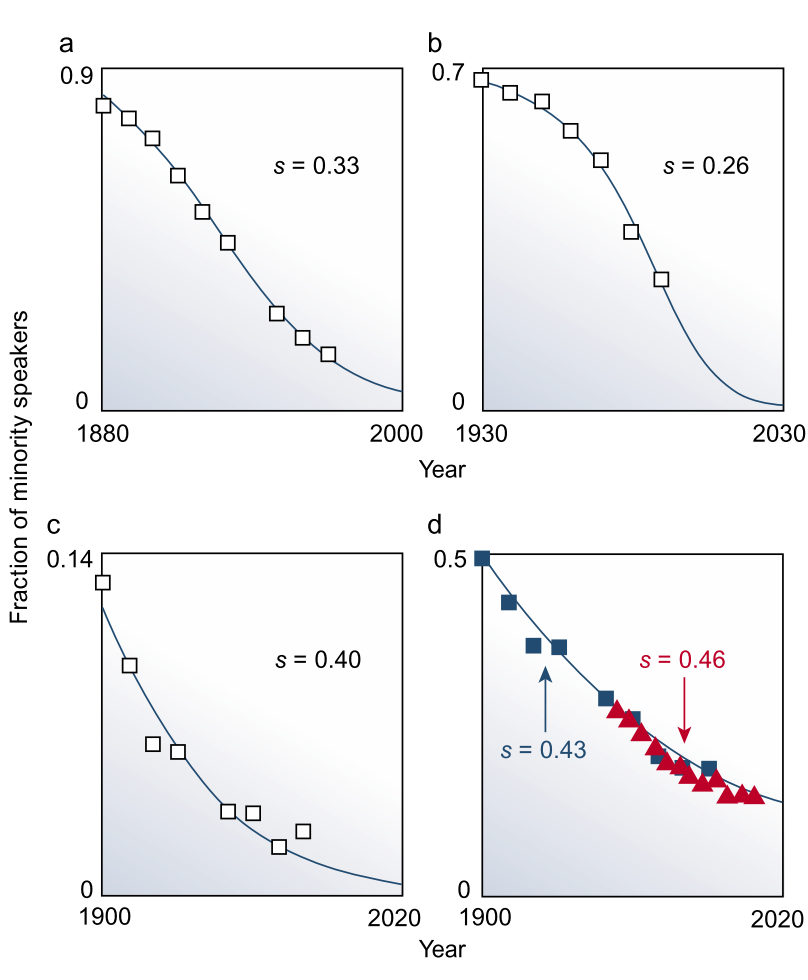
作者最后讨论了两种语言共存现象，这种情况可解释为操不同语言者空间或社会阶层的分离。

即他们之间的联系很少。