传播子和路径积分

路径积分 量子力学 传播子 费曼

---

传播子

绘景回顾

薛定谔绘景（S.P.）下，态矢量$\left| \alpha, t \right\rangle$含时，力学量不含时，态矢量随时间的演化符合薛定谔方程。

$$\begin{equation} i \hbar \frac{\partial }{\partial t} \left| \alpha, t \right\rangle = H \left| \alpha, t \right\rangle \end{equation}$$

其解可表示为：

$$\begin{equation} \left| \alpha, t \right\rangle = U(t) \left| \alpha \right\rangle \end{equation}$$

这里：

$$\begin{equation} U(t) = e^{-iHt / \hbar} \end{equation}$$

力学量$A$的本征值问题，

$$\begin{equation} A \left| a' \right\rangle = a' \left| a' \right\rangle \end{equation}$$

定义了基矢（basis）$\left| a' \right\rangle$，$\left| a' \right\rangle$也不含时。

态矢量$\left| \alpha, t \right\rangle$含时，可以用基矢$\left| a' \right\rangle$展开：

$$\begin{equation} \left| \alpha, t \right\rangle = \sum\limits_{a'} \left| a' \right\rangle \left\langle a' | \alpha, t \right\rangle \end{equation}$$

这里含时的部分被包含在因子$\left\langle a' | \alpha, t \right\rangle$中。

对海森堡绘景（H.P.）而言，态矢量不含时，比如就取$t=0$时刻时候的态矢量，记作：$\left| \alpha \right\rangle$。力学量含时，

$$\begin{equation} A(t) = U^\dagger (t) A U (t) \end{equation}$$

符合海森堡运动方程，

$$\begin{equation} i \hbar \dot A = [A, H] \end{equation}$$

现在来考虑H.P.下力学量$A(t)$的本征值问题：

$$\begin{equation} A(t) \left| a', t \right\rangle = a' \left| a', t \right\rangle \end{equation}$$

考虑到，

$$\begin{equation} U^\dagger A U U^\dagger \left| a' \right\rangle = a' U^\dagger \left| a' \right\rangle \end{equation}$$

H.P.下的基矢是：

$$\begin{equation} \left| a', t \right\rangle = U^\dagger \left| a' \right\rangle \end{equation}$$

看起来和S.P.下态矢量$\left| \alpha , t \right\rangle$随时间的演化$\left| \alpha , t \right\rangle = U \left| \alpha \right\rangle$类似，但方向正好相反。

传播子

在S.P.下，给定量子系统$H = \frac{p^2}{2m} + V$，考虑态矢量由$\left| \alpha , t_0 \right\rangle$演化到$\left| \alpha , t \right\rangle$，

$$\begin{equation} \left| \alpha , t \right\rangle = e^{-i H (t - t_0) / \hbar} \left| \alpha , t_0 \right\rangle \end{equation}$$

考虑$[A, H ] = 0$，基矢$\left| a' \right\rangle$同时也是$H$的本征矢，$H \left| a' \right\rangle = E_{a'} \left| a' \right\rangle$，因此：

$$\begin{equation} \left| \alpha , t \right\rangle = \sum\limits_{a'} \left| a' \right\rangle \left\langle a' | \alpha, t_0 \right\rangle e^{-i E_{a'} (t - t_0) / \hbar} \end{equation}$$

左乘$\left\langle x' \right|$，把上式变到位置表象，

$$\begin{equation} \left\langle x' | \alpha, t \right\rangle = \sum\limits_{a'} \left\langle x' | a' \right\rangle \left\langle a' | \alpha, t_0 \right\rangle e^{- i E_{a'} (t - t_0) / \hbar} \end{equation}$$

把因子$\left\langle a' | \alpha, t_0 \right\rangle$表示为位置表象，

$$\begin{equation} \left\langle a' | \alpha, t_0 \right\rangle = \int d^3 x \left\langle a' | x' \right\rangle \left\langle x' | \alpha, t_0 \right\rangle \end{equation}$$

为了避免歧义，把$\left\langle x' | \alpha, t \right\rangle$中的$x'$改记为$x''$，

$$\begin{equation} \left\langle x'' | \alpha, t \right\rangle = \int d^3 x' \sum\limits_{a'} \left\langle x'' | a' \right\rangle \left\langle a' | x' \right\rangle e^{- i E_{a'} (t - t_0) / \hbar} \left\langle x' | \alpha, t_0 \right\rangle \end{equation}$$

定义积分的核（Kernel）为$K(x'', t; x', t_0)$，

$$\begin{equation} K(x'', t; x', t_0) = \sum\limits_{a'} \left\langle x'' | a' \right\rangle \left\langle a' | x' \right\rangle e^{- i E_{a'} (t - t_0) / \hbar} \end{equation}$$

并用波动力学中的波函数对上式进行改写，

$$\begin{equation} \psi_\alpha (x'', t ) = \int d^3 x' K(x'', t; x', t_0) \psi_\alpha (x', t_0 ) \end{equation}$$

我们称$K$为传播子，即描述由时空中$x', t_0$传播到$x'', t$的行为。传播子与初始时刻的波函数$\psi_\alpha (x', t_0 )$无关，它是物理系统（$H$，这里就是$V$）本身性质的反映。

只要知道$\psi_\alpha (x', t_0 )$和$K$，就可知道$t > t_0$时刻的波函数$\psi_\alpha (x'', t )$。即是决定的，是因果律的。

$$i \xrightarrow{K}{} f$$

传播子的性质

（1）对$t > t_0$，传播子$K$符合薛定谔方程（S.E.）

（2）当$t \to t_0$时，传播子是德尔塔函数，

$$\begin{equation} \lim\limits_{t \to t_0} K = \lim\limits_{t \to t_0} \sum\limits_{a'} \left\langle x'' | a' \right\rangle \left\langle a' | x' \right\rangle e^{- i E_a' (t - t_0) / \hbar} = \left\langle x'' | x' \right\rangle \end{equation}$$

（3）$K$可表示为：

$$\begin{equation} K = \left\langle x'' \right| e^{- i H (t - t_0) / \hbar} \left| x' \right\rangle \end{equation}$$

证明：

$$\begin{equation*} K = \sum\limits_{a'} \left\langle x'' \right| e^{- i H (t - t_0) / \hbar} \left| a' \right\rangle \left\langle a' | x' \right\rangle = ... \end{equation*}$$

（4）$K$是格林函数（G.F.）

与电动力学中给定电荷分布求电动势类比，

$$\begin{equation} \phi(x) = \int d^3 x' \frac{\rho (x')}{ \left| x - x' \right| } \end{equation}$$

这里$\phi(x)$和$\psi_\alpha (x'', t)$对应，$\rho(x')$和$\psi_\alpha (x', t_0)$对应，而$\frac{1}{ \left| x - x' \right| }$和传播子$K$对应，都是积分的核。

$\frac{1}{ \left| x - x' \right| }$是微分方程$\nabla \cdot \nabla \frac{1}{ \left| x - x' \right| } = \delta^3 (x- x')$的解，类似地$K$是如下方程的解，

$$\begin{equation} \left[ i \hbar \frac{\partial }{\partial t} + \frac{\hbar^2}{ 2m} \nabla''^2 - V(x'') \right] K = i \hbar \delta^3 (x'' - x') \delta (t - t_0) \end{equation}$$

即：

$$\begin{equation} \left[ i \hbar \frac{\partial }{\partial t} - H \right] K = i \hbar \delta^3 (x'' - x') \delta (t - t_0) \end{equation}$$

边条件是$t < t_0$时，$K = 0$。对应推迟解，或符合因果律的解（时间在前的影响时间在后的，而非相反）。

$K$就是数学上的格林函数（Green Function，G.F.），其定义为微分算子作用于格林函数等于德尔塔函数，即$\hat L G(x,s) = \delta(x-s)$。

海森堡绘景下的传播子

传播子$K (x'',t; x',t_0) = \left\langle x'' \right| e^{- i H (t - t_0) / \hbar} \left| x' \right\rangle$是在薛定谔绘景（S.P.）下的定义。

在海森堡绘景下，利用$\left| a' , t \right\rangle = U^\dagger \left| a' \right\rangle$

$$\begin{equation} K = \left\langle x'' \right| U(t) U^\dagger (t_0 ) \left| x' \right\rangle = \left\langle x'', t | x', t_0 \right\rangle \end{equation}$$

传播子$K$即变换幅（Transition amplitude），$\left\langle x'', t | x', t_0 \right\rangle$的含义是“粒子”由$x', t_0$出发，传播到$x'', t$处的几率幅。

路径积分

变换幅

H.P.下，传播子$K(x,t;x_0,t_0)$可写为初始时刻位置算符本征矢$\left| x_0, t_0 \right\rangle$与终了时刻位置算符本征矢$\left| x,t \right\rangle$的内积。$\left| x_0, t_0 \right\rangle$与$\left| x, t \right\rangle$分别都可构成表示量子态的基矢量。传播子的地位就相当于由初始时刻（A）到终了时刻（B）的表象变换，

$$\begin{equation} K(xt; x_0,t_0) = \left\langle x,t | x_0, t_0 \right\rangle \end{equation}$$

就相当于是AB表象之间的变换矩阵，现在因为位置的取值是连续的，我们可以管$\left\langle x,t | x_0, t_0 \right\rangle$叫变换函数（transformation function），它把不同时刻（$t$和$t_0$）的两套基矢联系起来。

$t> t_0$，在$t$与$t_0$之间我们总可插入一个时刻$t_1$，量子态由$t_0$开始，先演化到$t_1$，最后演化到终了时刻$t$，这相当于我们在变换幅$\left\langle x,t | x_0, t_0 \right\rangle$中间插入一个单位算符：

$$\begin{equation} 1 = \int d^3 x_1 \left| x_1, t_1 \right\rangle \left\langle x_1, t_2 \right| \end{equation}$$

这里$\left| x_1, t_1 \right\rangle$是$t_1$时刻，位置算符的本征矢，它的集合也构成一个基矢。现在变换幅表示为：

$$\begin{equation} \left\langle x,t | x_0, t_0 \right\rangle = \int d^3 x_1 \left\langle x,t | x_1, t_1 \right\rangle \left\langle x_1 , t_1 | x_0, t_0 \right\rangle \end{equation}$$

上式称为变换幅的合成性质（composition property），利用这一性质我们可以继续插入不同时刻的位置算符的本征矢，直至相邻时间间隔$d t \to 0$为止。当$d t \to 0$时，变换幅将有可能表现为简单的形式，循此思路，费曼提出了量子力学的路径积分表示，这是不同于波动力学和矩阵力学的第三种量子力学的表述方式。

路径求和

假设我们在$t_0$到$t$区间里插入$N$个时刻，$t_1, t_2, ..., t_N$，当$N \to \infty$时，每相邻时间间隔$\frac{t - t_0}{N} \to 0$。

现在，$x_0,t_0$到$x,t$的变换幅可表示为：

$$\begin{equation} \left\langle x,t | x_0, t_0 \right\rangle = \int d^3 x_N ... \int d^3 x_1 \left\langle x, t | x_N, t_N \right\rangle \left\langle ... \right\rangle ... \left\langle x_1, t_1 | x_0 , t_0 \right\rangle \end{equation}$$

积分就是求和，被求和的项是：

$$\begin{equation*} \left\langle x,t | N \right\rangle \left\langle N | N-1 \right\rangle ... \left\langle 2 | 1 \right\rangle \left\langle 1 | 0 \right\rangle \end{equation*}$$

共$N+1$个无穷小时间间隔的传播子相乘，如果我们追踪每个时间的节点的话，首先由$t_0$出发，$0 \to 1$是第一个传播子，0点作为初始点是固定的，但1点作为积分中的哑元需遍历全空间，假如追踪某个特定的1点，将继续传播到2，$1 \to 2$，同样2点也需遍历全空间，……，最后由N点回到终了时刻$t$。

从$t_0$到$t$构成了一个互相连接的传播子路径，但这个路径中只有首、尾两点是固定的，中间N个节点可以有多种选择，并且需遍历整个空间。这样总的传播子（或变换幅）$\left\langle x,t | x_0, t_0 \right\rangle$就相当于是首尾固定情况下所有“各种路径”的求和。

$$\begin{equation} \left\langle x,t | x_0, t_0 \right\rangle \propto \sum\limits_{All Paths} \left\langle x, t | x_N, t_N \right\rangle \left\langle ... \right\rangle ... \left\langle x_1, t_1 | x_0 , t_0 \right\rangle \end{equation}$$

量子力学中真正关键的是相位，现在每一个无穷小传播子都带着一个相位，所有这些相位要加起来才对应某条路径的相位，不同路径的相位还会发生“干涉”，正是这个缘由导致了不同于经典物理的（丰富的）量子行为。

经典物理中涉及路径的基本原理有光程取极值原理（光学中的费马原理）和力学中的最小作用量原理（哈密顿原理）。

前者是说光实际走过的路径是使光程取极值的路径，表示成数学形式就是：

$$\begin{equation} \delta \int n(x) dx = 0 \end{equation}$$

后者是说对经典力学而言，粒子实际走过的路径是使作用量取极值的路径，即：

$$\begin{equation} \delta \int_{t_1}^{t_2} L_c (x, \dot x) dt = 0 \end{equation}$$

由费马原理可解释光的直线传播，反射、折射定律等。由哈密顿原理，我们可求出粒子运动的动力学方程：

$$\begin{equation} \frac{d}{dt } \frac{\partial L_c}{\partial \dot x} - \frac{\partial L_c }{\partial x} = 0 \end{equation}$$

上式其实就是：$m \ddot x = - \frac{\partial V}{ \partial x}$

既然通过（和路径相关的）作用量取极值的方法可以建立经典力学，那么我们是否可类似地基于路径和作用量的概念建立量子力学呢？这个思路对物理学家来说并不陌生，比如量子力学的对易式就可与经典力学中的泊松括号类比。

尽管如此量子力学和经典力学的结果还是有很大区别的，比如经典力学求出来的是一条确定的轨迹，而量子力学中的“对各种路径”求和，则表明每一条路径（而非只有某个特殊的路径）都会对最终的变换幅有贡献。我们期待当$\hbar \to 0$时，量子力学的结果会无限趋近经典力学的结果。

$$Q.M. \xrightarrow{\hbar \to 0} C.M.$$

费曼的路径积分

量子力学的路径积分表示是由费曼完成的，费曼研究生的时候在狄拉克的书里读到：传播子$\left\langle x_2, t_2 | x_1, t_1 \right\rangle$就相当于（correspons to）是：

$$\begin{equation} \exp \left[ {\frac{i \int_{t_1}^{t_2} L_c(x, \dot x) dt}{\hbar}} \right] \end{equation}$$

积分部分是作用量（Action）$S$，其量纲与普朗克常数$\hbar$相同。$e$指数部分的$\frac{i S(2,1)}{\hbar}$给定了传播子$\left\langle x_2, t_2 | x_1, t_1 \right\rangle$的相位。但传播子的振幅是什么，狄拉克并没有继续讨论。费曼读到这段后，深感困惑，他想弄明白这个“相当于”指的到底是什么，是“等于”，还是“正比于”，还是别的什么关系……经过计算，费曼发现这个“相当于”是“正比于”的意思，并求出了比例因子。

$\hbar$处于分母位置还能解释为什么当$\hbar \to 0$时，量子行为会过渡到经典行为。量子行为对应的是所有路径求和，而经典路径对应的是只有最小作用量的路径会凸显出来。最小作用量的路径就是使$\delta S = 0$的路径，在这个路径的附近还有很多其它路径，这些路径与最小作用量路径的偏离就是$\delta S$，而$\hbar$是趋于0的，但并不是0，在这个条件下，最小作用量附近路径的相位就是$e^{\frac{i \delta S}{ \hbar}}$，都趋于1，即相长干涉，因此经典路径的贡献就会加强凸显出来。

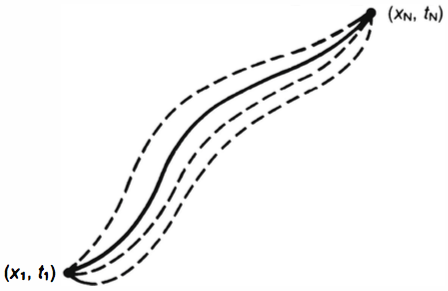
对一般的路径 $\delta S \neq 0$，这意味着它和它附近路径的相位差是$\frac {\delta S} { \hbar }$，这里$\delta S \neq 0$，而$\hbar \to 0$，$\frac{\delta S}{\hbar}$ 就是个很大的不确定的数，反映在相位上就是任意相位，这样对一般路径而言，它附近的那些路径与它的相位差是任意取值的，因此会互相抵消掉。这样在 $\hbar \to 0$ 时，那些非经典路径的变换幅就只能取0了。

当然费曼最感困惑的是为什么狄拉克自己没有继续这个思路，进而提出量子力学的路径积分表示。据说他曾经就此问过狄拉克，但狄拉克没有告诉他。

无穷小的传播子

现在我们来计算某个无穷小的传播子：

$$\begin{equation} \left\langle x_n, t_n | x_{n-1}, t_{n-1} \right\rangle = \frac{1}{w(\Delta t)} e^{iS(n, n-1) / \hbar} \end{equation}$$

这里$\Delta t = t_n - t_{n-1}$，$\frac{1}{w(\Delta t)}$是比例因子，假设它只和$\Delta t$有关。现在来计算$S(n, n-1)$，

$$\begin{equation} S(n, n-1) = \int_{t_{n-1}}^{t_n} \left( \frac{m \dot x^2}{2} - V(x) \right) dt \end{equation}$$

由于$\Delta t \to 0$，我们可以把积分进行改写，

$$\begin{equation} S(n, n-1) = \left[ \frac{m}{2} \left( \frac{x_n - x_{n-1} }{\Delta t} \right)^2 -V \left( \frac{x_n + x_{n-1}}{2} \right) \right] \Delta t \end{equation}$$

假设我们研究的是自由粒子，$V=0$，现在无穷小的传播子变为：

$$\begin{equation} \left\langle x_n, t_n | x_{n-1}, t_{n-1} \right\rangle = \frac{1}{w(\Delta t)} e^{ \frac{i m ( x_n - x_{n-1} )^2 }{ 2 \hbar \Delta t} } \end{equation}$$

从样子上看，很像一个钟形函数（bell function，或高斯函数），$\Delta t$正比于钟形函数的宽度，当$\Delta t$趋于零时，钟形函数会变得无穷窄，即趋于一个德尔塔函数的样子。

当$\Delta t \to 0$时，即$t_n \to t_{n-1}$时，

$$\begin{equation} \lim\limits_{t_n \to t_{n-1}} \left\langle x_n, t_n | x_{n-1}, t_{n-1} \right\rangle = \delta(x_n - x_{n-1}) \end{equation}$$

我们引入新的变量$\xi = x_n - x_{n-1}$，现在的问题就是当$\frac{1}{w(\Delta t)} =?$的时候，

$$\begin{equation} \lim\limits_{\Delta t \to 0} \frac{1}{w (\Delta t)} e^{\frac{i m \xi^2}{2 \hbar \Delta t}} = \delta (\xi) \end{equation}$$

考虑到德尔塔函数的性质，

$$\begin{equation} \int \delta(\xi) d \xi = \lim\limits_{\Delta t \to 0} \int d \xi \frac{1}{w (\Delta t)} e^{\frac{i m \xi^2}{2 \hbar \Delta t}} = 1 \end{equation}$$

由高斯积分[1]，

$$\begin{equation} \int d \xi e^{\frac{i m \xi^2 }{ 2 \hbar \Delta t} } = \sqrt{ \frac{ 2 \pi i \hbar \Delta t }{m } } \end{equation}$$

我们就得到：

$$\begin{equation} \frac{1}{w(\Delta t )} = \sqrt{\frac{m }{2 \pi i \hbar \Delta t} } \end{equation}$$

最终我们就得到传播子的费曼路径积分表示：

$$\begin{equation} \left\langle x_N,t_N | x_0, t_0 \right\rangle = \lim\limits_{N \to \infty} \left( \frac{m }{2 \pi i \hbar \Delta t } \right)^{N/2} \int dx_{N-1} ... \int dx_1 \prod\limits_{n=1}^{n = N} e^{\frac{iS(n, n-1)}{\hbar}} \end{equation}$$

我们可示意性地将其改写为：

$$\begin{equation} \left\langle x_N,t_N | x_0, t_0 \right\rangle = \int_{x_0}^{x_N} D[x(t)] e^{ \frac{ i }{ \hbar} \int_{t_0}^{t_N} L_c(x, \dot x) dt } \end{equation}$$

如此繁复的积分使得路径积分法在求解（非相对论）量子力学问题时没什么优势，但当使用路径积分求解量子场论（或多体）问题时却会变得很强大。

最后，我们还可验证如此求出的传播子$\left\langle x,t | x_0, t_0 \right\rangle$符合薛定谔方程（S.E.），即：

$$\begin{equation} i \hbar \frac{\partial }{\partial t } \left\langle x,t | x_0, t_0 \right\rangle = - \frac{\hbar^2}{ 2 m } \frac{\partial^2 }{\partial x^2 } \left\langle x,t | x_0, t_0 \right\rangle + V (x) \left\langle x,t | x_0, t_0 \right\rangle \end{equation}$$

具体过程略。

参考

• J. J. Sakurai, Modern Quantum Mechanics, $\S 2.2$，$\S 2.5$

• R. P. Feynman, The Development of the Space-Time View of Quantum Electrodynamics.