导体为什么能导电

问题网络计划

---

“导”和“电”

导体可以定义为能导电的物体，这里物体可以看做是自明的，但需要约定：是固体、液体、气体？或者其他物质存在形态？

导电可以分解为“导”和“电”两个概念。

“导”，组词可以组“导管”、“导流”，“传导”……其核心含义是（某物）从空间中的一个地方流动到另一个地方。

典型的例子就是水流，及看起来像是水流的东西，比如粒子流。

我们可以用流量来描述流，定义为单位时间穿过某平面的物质的量。

$$J = \frac{\Delta Q}{\Delta t}$$

还可定义流密度，即再对单位截面积做个运算：

$$j = \frac{\Delta Q}{\Delta S \Delta t}$$

再来讨论“电”，

电有惊奇，令人惊讶的意思，换句话说“电现象”是人稍晚才会在日常生活中经验到的新现象。

这里我们可以先罗列我们生活中碰到的电现象：

• 干燥的冬日，我们在脱衣服的时候，身体会产生静电，有时候这个静电还挺厉害，一个带静电的人去触摸其他物体的时候，因放电会发出响亮的“噼啪”声。甚至当这个人去触摸电脑的时候，电脑里的电路有可能会被击坏。

• 取一节干电池，用电线连接电池的正极和负极，我们会看到当电线接触电池的电极的时候，会发出细小，但可清晰分辨的火花。

更多电现象的例子：

• 古代埃及人，通过尼罗河中的电鱼（Thunderer of the Nile），认识到电现象；

• 乌云靠近，电闪雷鸣，古希腊人认为宙斯掌握雷电；

• 毛皮摩擦琥珀，然后琥珀具有吸引小物体的能力，后来吉尔伯特仔细研究了这类现象并以新造拉丁词“electricus”描述这一现象，直译就是琥珀的（of amber），或类似琥珀的（like amber）。

• 伽伐尼发现生物电现象。

（伽伐尼）在实验室解剖青蛙，把剥了皮的蛙腿，用刀尖碰蛙腿上外露的神经时，蛙腿剧烈地痉挛……

自然我们就有一个问题：

以上这些现象是否属于一类现象？

比如：富兰克林曾经在电闪雷鸣的天气里放风筝，把天上的电引下来，然后证明和地上通过摩擦产生的电并无区别。

富兰克林糊了个风筝，风筝用杉树枝作骨架，扎成菱形，蒙上一层不易湿透的绸子，风筝的上端装了一根一英尺长的尖铁丝，将它与牵风筝的亚麻线系在一起，亚麻线的下端接在一段不长的丝绳上，以便将风筝拉住，丝绳的末端拴了一把金属钥匙。……

当风筝上面漂浮着带雷电的云时，尖铁丝立即从云中取得了“电火”。富兰克林发现与丝绳连在一起的亚麻线上，有几处散开的纤维直竖了起来，且能被手指吸引。他用食指靠近钥匙圈，骤然间，一些电火花从他食指上闪过，与摩擦生电时发生的电火花没有两样。

莱顿瓶

莱顿瓶就是一个玻璃瓶，玻璃瓶的内外各自铺满金属箔（Foil），瓶塞处会插上一个金属棍，一端是金属球露出瓶口，另一端是金属链与瓶内的金属箔接触。

从效果上说，这个构造可以“储存”电，因此我们可以管它叫“电的容器”，简称电容[1]。

导电现象

首先先举一个身边的例子：

• 干电池、电线和小灯泡构成电路，我们发现换不同材质、长度、粗细的电线都能点燃电灯泡。

历史上的一些有趣实验：

• 格雷（Stephen Gray）发现摩擦过的玻璃棒能使与它接触的木塞也带电，并能吸引细小的物体，进一步，如果用绳索一端拴在木塞上，另一端系一个玻璃球，发现电可以被传得很远，即：远处的玻璃球也能吸引细小的物体。甚至用人代替绳索，也能产生同样的效果。即人也是“导电”的。

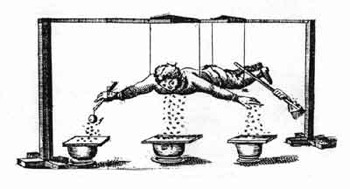
• 700个修士在巴黎圣母院前手拉手排成一个大圆圈，排头的人用手拿住莱顿瓶，排尾的人手握莱顿瓶的引线。莱顿瓶放电时，整个队伍在同一瞬间突然跳了起来。

欧姆定律

首先电流应如何量度？考虑到电是个“新奇”的物理现象，我们很难直接量度它，我们只能通过电流产生的物理效应来量度它。

比如欧姆就是用电流的磁效应来量度它的：

欧姆把奥斯特关于电流磁效应的发现和库伦扭秤的方法巧妙地结合起来，设计了一个电流扭力秤，用它来测量电流强度。

历史上欧姆是用温差电偶做电源来发现欧姆定律的。

$$R = \frac{U}{I}$$

我们现在可以构想如下简单的实验来检验欧姆定律：

在一张A4纸上用B2铅笔画出几个长度不同，宽度不同，粗细均匀的铅笔道，然后用电流计测量通过铅笔道的电流。

我们可小结出：

• 电流正比于铅笔道的宽度；
• 电流反比于铅笔道的长度；

假如我们用几个电池串联在一起给铅笔道供电，

• 电流正比于电压（即电池的个数）。

一般欧姆定律被陈述为：电阻（$R$）正比于“线装材料”的长度（$l$），反比于“线状材料”的截面积（$S$）。比例系数被定义为电阻率（$\rho$）。

$$R = \rho \frac{l}{S}$$

这里$\rho$只与材料性质有关。

金属的Drude模型

欧姆定律并不一定总成立。但对金属一般而言是成立的。

金属的Drude模型可以解释欧姆定律。

假设金属中的载流子是电子，每个电子的带电量是$e$。金属中的电子密度是$n$，金属中的电流是：

$$I = \frac{\Delta Q}{\Delta t } = \frac{e n S v \Delta t }{\Delta t } = e n S v$$

这里$S$是金属的截面积，$v$是金属中电子的平均运动速度。

假设没有加电场的时候，金属中的电子处在热平衡状态，平均而言，电子没有整体的定向运动，或者说金属中电子的平均速度是0（当然平均速率并不是0）。

现在我在金属的两端加以定向电场$E$，假设金属长度是$l$，金属两端的电压（$U$）就是：

$$U = E l$$

同时电子会在电场的作用下加速运动，但考虑到金属中有大量正电背景（甚至各种缺陷），电子运动一段时间后，就会和正电背景或者缺陷碰撞，碰撞后电子重新回复到热的平衡状态，然后重新被金属中的电场加速。

换句话说金属在电场作用下的定向运动会被频繁的碰撞限制住，最多只能加速到某个特征速度$v$，

根据冲量原理：

$$m v = F \tau = e E \tau$$

这里$\tau$是碰撞发生的特征时间，即大概这么长时间，电子就要和正电背景或缺陷碰撞一次。

现在：

$$I = \frac{n e^2 S E \tau}{m}$$

考虑到电压是

$$U = E l$$

现在计算电阻：

$$R = \frac{m E l }{n e^2 S E \tau} = \frac{m}{n e^2 \tau} \frac{l}{S}$$

电阻率是：

$$\rho = \frac{m}{n e^2 \tau}$$

或者写成电阻率的倒数——电导率（$\sigma$）的形式：

$$\sigma = \frac{n e^2 \tau }{m }$$

参考

• Wikipedia: Drude Model
• 金属的德鲁德模型