穿越地心

万有引力 简谐振动

---

@季燕江

自由下落

北京的经纬度是：$N: 40^o$，$E: 116^o$，假如我们从北京挖一条穿过地心的隧道，这条隧道将从地球的另一边出来，位置是：$S: 40^o$，$W: 64^o$，这个地方正好是阿根廷的南部。

假如我们乘坐一个能够耐高温的车厢，从北京这一端沿着隧道自由地落下，我们要花多长时间才能到达阿根廷呢？经过估算，这个时间非常短，大约只有42分钟，比乘坐飞机要快得多。

万有引力

根据牛顿的万有引力定律，苹果落地时因为苹果和地球之间有引力，引力使苹果落向地面，力的大小是：

$$F = mg$$

这里$m$表示苹果的质量，$g$表示地球表面的重力加速度，其大小是$9.8 m \cdot s^{-2}$。

如果苹果是落向我们挖的那条隧道呢？引力会吸引着苹果继续落下，一旦苹果掉进隧道，它所受到的引力就变小了，因为地球的一部分已经在它身后了。

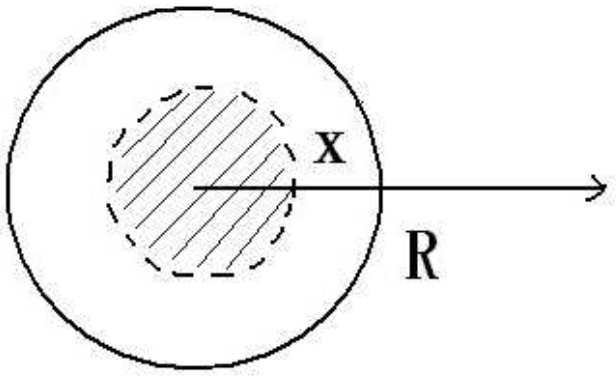
假设苹果现在的位置在$x$处，即苹果落到了距离地心$x$的地方。以$x$为半径，我们可围绕地心画出一个球形的区域，如图所示阴影的区域。我们可以证明，对于平方反比的力，比如万有引力和静电库仑力，只有阴影部分的质量需要考虑，而非阴影部分与苹果的相互作用正好互相抵消掉了。

因此质量$m$物体在距离球心$x$处的万有引力是：

$$F = - \frac{G M_x m}{x^2}$$

这里$M_x$表示阴影部分的质量，假设地球质量是均匀分布的，则：

$$M_x = \frac{4 \pi x^3}{3} \cdot \rho$$

这里$\rho$是地球的密度：

$$\rho = \frac{M_E}{V_E}$$

$M_E$表示地球的质量，$V_E$表示地球的体积，与地球半径$R_E$的关系是：$V_E = \frac{4 \pi}{3} R_E^3$。因此：

$$M_x = \frac{r^3}{R_E^3} M_E$$

根据万有引力定律，质量为$m$物体在距离地球中心$x$（$< R_E$）处的受力是：

$$F_x = -\frac{G M_x m}{x^2} = - \frac{G M_E x}{R_E^3} m$$

这里$G$是万有引力常数。负号表示受力的方向是指向地球中心的。

现在需要求解运动方程（牛顿第二定律）：

$$F = ma$$

即：

$$\ddot x = - \frac{G M_E x}{R_E^3}$$

这个方程的特点是：

1.与质量$m$无关，这意味着不论质量多大，只要初始条件相同，物体下落的快慢和过程都是一样的。

2.形式上与弹簧振子的运动方程相同：$m \ddot x + k x = 0$

简谐振动

我们现在需要回忆弹簧振子方程的求解，

$$\ddot x + \frac{k}{m} x = 0$$

这里$m$是物体的质量，$k$是弹簧的弹性系数。令：$\omega^2 = \frac{k}{m}$，方程的解是：

$$x(t) = A \cos \omega t$$

这里$A$是振幅。并且假设当时刻$t=0$时，$x_0 = A$。对$x(t)$依次求导可得：

$$\dot x = - \omega A \sin \omega t$$

$$\ddot x = - \omega^2 A \cos \omega t$$

当时刻$t = 0$时，速度最小，$v_0 = 0$，当$\omega t = \frac{\pi}{2}$时，速度达到最大，其大小是：

$$v_{max} = \omega A$$

当$\omega t = 2 \pi$时，物体运动状态重新回到初始的状况，然后就“循环往复”了，这是一种周期运动，周期是：

$$T = 2 \pi \sqrt{ \frac{m}{k} }$$

地心快车

对于我们现在的问题而言，$\omega^2$是：

$$\omega^2 = \frac{k}{m} = \frac{GM_E}{R_E^3}$$

质量为$m$的物体（地心快车）由静止自由下落，穿过直达地心的隧道，将会运动到地球的另一端，对应的时间是$\frac{T}{2}$，此时物体的运动速度为0，如果不用机械手抓住它，物体将会重新落回去，再次穿过地心，走一个来回，所需时间是$T$，

$$T = 2 \pi R_E \sqrt{ \frac{R_E}{G M_E} }$$

现在代入以下物理量的取值，

万有引力常数	$G$	$6.673 \times 10^{-11} m^3 \cdot kg^{-1} \cdot s^{-2}$
地球半径	$R_E$	$6.378 \times 10^6 m$
地球质量	$M_E$	$5.97 \times 10^{24} kg$

可以估算出：$T \approx 5000 s$，相当于1.4小时，或说是1小时24分钟。那么搭乘“地心快车”，由北京到阿根廷需要多长时间呢？只需要$\frac{T}{2}$，即大约42分钟。

这个速度可以说是相当快的，我们可以把它和声音的速度比较，声音的速度（$v_s$）是：

$$v_s = 340 m \cdot s^{-1}$$

地心快车的平均速度是：

$$\bar v = \frac{4 R_E}{T} \approx 5100 m \cdot s^{-1}$$

即相当于是音速的大约15倍，而地心快车的最大速度是：

$$v_{max} = \omega R_E = \sqrt{ \frac{G M_E}{R_E} } \approx 7900 m \cdot s^{-1}$$

即相当于是音速的约23倍。

现在，假设我们乘坐商务喷气客机来完成一次这样的旅行，从北京到阿根廷，飞越半个地球的旅行，需要的时间是：

$$time = \frac{\pi R_E}{v_p}$$

取飞机的巡航速度（$v_p$）为：

$$v_p = 1000 km/hour \approx 278 m \cdot s^{-1}$$

解出所需时间为约$7.2 \times 10^4 s$，即相当于是大约20小时。

扩展阅读

考虑到地球的质量并非是均匀分布的，大致来说地球由外到内可分为三个区域：（1）地壳，（2）地幔和（3）地核。地核的密度要远高于其他两个区域。

由于这个原因，如果我们实际开凿这样一个隧道的话，地心快车的速度还可以更快，根据wolfram网站给出的估算往返将需要大约46分，即单程只要23分。

网址：The Science of Total Recall

考虑到地核温度很高，约$4000-6000{}^o C$，实际开凿这样一条隧道也许并不可能，但我们可设想在未来的某个人工星体——比如星球大战中的死星——上设计很多这种利用引力加速的快速列车。