@jiyanjiang
2022-07-19T23:43:27.000000Z
字数 8537
阅读 2276
狭义相对论前传
狭义相对论 光速的测量
@季燕江
以太假说
量子力学和相对论是现代物理学的两大支柱,相对于量子力学来说,相对论几乎是爱因斯坦一人的功绩,至少对外行人来说是这样。相对论本身又分狭义相对论和广义相对论,其中狭义相对论是每个具有高中以上物理和数学知识的人可以掌握的,从狭义相对论的基本假设出发,通过求解一系列线性方程组,我们可以得到狭义相对论的主要公式,比如著名的:。这几乎是非专业工作者可以轻松掌握的最后一个物理理论,但如果你要系统地学习量子力学或广义相对论,你就必须花大量的时间,除了阅读和思考,计算也是必备的。
现在我们就来讨论相对论的创建,首先是狭义相对论的创建。要讨论这一话题,我们首先需要回忆1900年时的物理学状况。1900年时,物理学家们已经得到了三大理论:经典力学、经典电磁学和经典统计力学(就是经典的热力学与统计物理),统称经典物理学。我们所熟悉的:行星的运动、炮弹的运动、声音现象、热现象、电磁学现象、光学现象等都已经很好地被解释。自然界中如此多样的物理现象竟然被三个基本理论所解释,这本身就是个巨大的成就。
如果我们回顾一下伽利略(Galileo Galilei, 1564-1642)对科学研究的态度的话,我们会感叹伽利略对存在一个统辖一切的终极理论是否太悲观了呢?伽利略认为:
由观察或实验得到的每个事实及其直接的和不可避免的推论都按照本来面目被人接受,不管人们怎样想把自然界一下子收服在理性的管辖之下。许多孤立的事实的协和是慢慢显露出来的......要把所有的科学的和哲学的知识融合成一个更高的、统摄一切的统一体,即使还不是绝不可能的,也须推迟到遥远的将来。
仅仅过了300年,物理学家因为经典物理学的伟大成就而感到满足,并开始憧憬物理学大厦的最终完成。开尔文勋爵是经历了19世纪物理学主要发展的学术权威,1900年,他在迎接20世纪的物理学年会上说:“物理世界的理论大厦已经建立起来了”,今后物理学家的工作就是在小数点之后再加上几位的“零碎修补工作”。同时开尔文也指出:“在物理世界的东方有两片乌云,一片是以太理论的困难(电磁学的参考系问题),一片是能量均分定理的困难(热辐射的理论解释)”。
开尔文的讲话再次证明科学发现本身是不可预测的,后来科学史的发展证明,20世纪上半叶非但不是对物理学大厦的修补,反而是自哥白尼革命后的第二次科学革命,相对论和量子力学就是第二次科学革命的成果。
但相对论和量子力学的出现并非历史上的突发事件,第二次科学革命的萌芽其实已经孕育在经典物理学内部了,开尔文指出的两片乌云正是新理论出现的征兆。
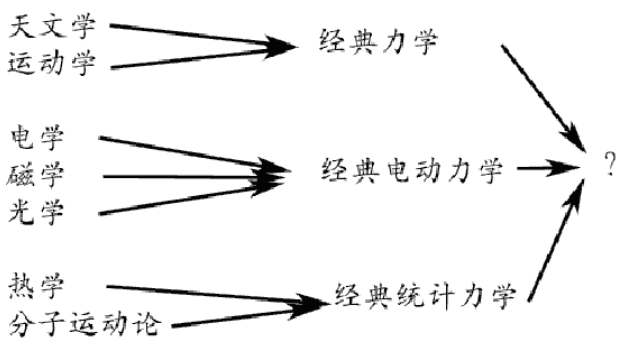
经典物理学有三个基本的理论,那么它们三者之间又是什么关系呢?如果不能将其统一为一个理论,但至少不应当是互相矛盾的。但是如果我们同时把三个理论中的任意两个利用于某些物理现象,会发现很难解释这些现象。这意味着我们需要对经典物理学进行修补,乃至完全放弃经典物理学建立新的理论。
以太理论的困难反映的是调和经典电动力学与经典力学的困难,而热辐射的理论解释则需要同时使用经典统计力学与经典电动力学。那么经典力学与经典统计力学之间呢?它们同样也存在着难题,发现这个难题的正是开尔文本人。利用经典力学和热力学理论,开尔文曾经估算过太阳系的最大年龄,他的结果是最大不超过几千万岁,但地质学和古生物学知识告诉我们地球上的生物至少已进化了几亿甚至几十亿年。
现在回到狭义相对论,要讨论狭义相对论的创建让我们首先讨论人类对光本性的认识。最初牛顿提出了粒子说,惠更斯则提出了波动说,牛顿的粒子说相对占了上风。但1801年杨氏双缝干涉实验之后,波动说逐渐占了上风。后来麦克斯韦提出电磁辐射理论,证明了光波就是电磁波,而赫兹实验也表明电磁波具有光波的一切性质。因此在1900年前后,物理学家确认光是一种波动,具体说就是电磁波。
而根据经典力学, 波动是需要有介质的,比如声波是在空气或水中传播的。因此光波即电磁波也需要一种介质,而这种因理论需要而假想出来的介质就被命名为以太。麦克斯韦写道:
人们想出了各种各样的以太。行星在其中漂浮的以太,电现象和磁现象赖以形成的以太,把人们的感觉从身体的这一部分传递到另一部分的以太等等。至今人们提出的,充满整个空间的以太已有三、四种。只有一种以太经受了考验,这就是由惠更斯为解释光的传播而想出的那种以太。
证明以太的存在是困难的,设想我们在真空中挥动手臂,我们并不会感到以太的存在,我们也无法用眼睛看到它,因为以太本身并不发光。但我们可以根据光的各种现象去推论以太的性质。比如:因为光在“真空”中也可传播,并还可通过各种光介质,因此以太是无所不在的,充满整个宇宙。因为电磁波是横波,以太应类似于固体具有切向的应力,但固体中即可传播横波又可传播纵波,因此以太又不是固体,因为它完全没有垂直方向的应力。因为光速是已知各种速度中最快的,因此以太应当是最“硬”的, 但我们又几乎无法感觉到它的存在。
为了理解这种具有奇异性质的以太,19世纪末的物理学家提出了很多模型,比如开尔文提出以太应该具有类似鞋匠所用鞋胶或鞋蜡的性质,这类物质具有这样的特性:当快速加上强力时,它们能像玻璃一样断开,但在很弱的力作用下,它们会象液体一样流动。麦克斯韦也曾构造过以太的机械模型,但所有这些努力都未取得成功。
光速的测量
测量光速对实验物理学家来说是个巨大的挑战,因为光的速度太快了,在我们的日常经验里光速就是无穷快的,我们一开灯,光瞬间就会充满整个房间。所以即使光速是有限的,它也会非常非常快,因此要成功地测量光速,我们需要精确精细地测量时间,或有个足够大的实验室。
伽利略曾尝试测量光速。他在一个漆黑的夜晚,让一个助手在约4.8公里远的小山顶上,放一个可用桶罩住的发光手灯,他自己也有一个这样的手灯。当两人都准备好以后,伽利略去掉罩在手灯上的桶,灯光会以光速传播到他的助手那里,助手一看见灯光,也立即拿掉罩在手灯上的桶,灯光也同样以光速传到伽利略那里。伽利略记录了从他第一次拿去手灯上的桶到看见助手灯光的这一段时间,再根据事先精确测定的两地间的距离,便可以计算出光速。可惜伽利略的实验失败了,因为人看到灯光到作出反应至少需要0.1秒的时间,而我们现在知道光速每秒是30万公里,显然4.8公里太短了。
但伽利略的另一项发明——望远镜,为光速的测量奠定了基础。1610年,伽利略用自己发明的望远镜首次发现了木星的四个卫星,并且发现木星的卫星围绕木星旋转一周的时间都是固定的,即我们通过望远镜可以确定木星卫星的公转周期。
天文方法
历史上第一次成功地测量光速,就是利用了木星卫星的“掩蚀”现象,所谓木星卫星的掩蚀指的是地球、木星和木星的卫星基本成一直线,木星的卫星恰好被木星遮挡,我们在地球上将观察不到木星的卫星,即木星的卫星被掩蚀。但由于木星和地球之间有相当长的一段距离,所以地球上的观察者会滞后一段时间观察到木星的卫星被木星遮挡。如果我们测量出木星的卫星绕木星公转的周期,我们将精确地预测每次木星的卫星被掩蚀的时间。
1675年,丹麦天文学家罗默(Olaf Roemer, 1644-1710)对木星的第一颗卫星(Io)进行了观测,当地球位于如下图A位置时,观测到木卫一公转周期是约42.5小时,由于公转周期是不变的,因此我们可预测下一次掩蚀发生的时间是42.5小时之后,再下一次应是85小时之后等等。但是,罗默发现这个预言并不准确。当地球由A逐渐向C运动时,下一次掩蚀发生的时间要比预测的推迟一点点,当过了大约半年时间,地球运行到C位置,而木星则由J1位置运行到J2位置(由于木星绕太阳运转周期比地球周期长得多(木星的公转周期是11年多),因此木星的运动在这里几乎可以忽略不计),此时木卫一发生掩蚀的时间已经比预言推迟了1000秒。
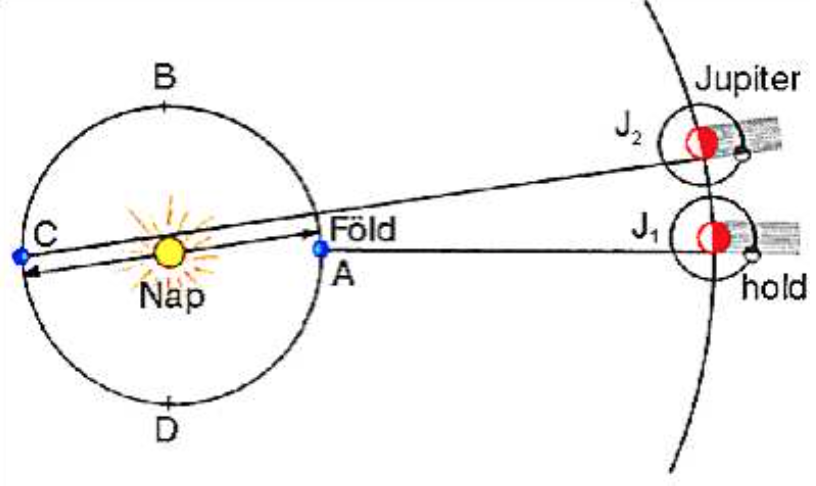
罗默很快意识到,如果认为光速是有限的话,这1000秒时间恰好对应光穿过地球轨道直径所需要的时间。那个时代,地球轨道直径被认为是大约2.76亿公里(正确值是约3.0亿公里),因此罗默得到的光速比正确值略小,但作为对光速的第一次成功测量,罗默的方法被载入了史册。
罗默的方法相当于是一个在“天文学尺度”上重做的伽利略实验,在这个实验中,伽利略的助手拿着灯(木卫一)逐渐远离我们,与此同时他按照一定周期(42.5小时)遮挡灯光,伽利略每次看到灯光被遮挡都要比上一次滞后一点点时间,如果助手退到足够远的话, 比如说是地球公转直径(),总的时间退迟将逐渐积累到可以测量的足够大数值(1000秒). 因此,光速()为:
在17-18世纪,利用天文现象,即使用足够大的实验室远比精确地测量时间要来得容易。在罗默之后,英国的布雷德利(James Bradley,1693-1762)又利用另外一种天文现象——光行差(aberration)现象,对光速进行了测量。
为了理解光行差现象,我们可以假设自己在雨中行走,假设没有风,雨滴是垂直落下的,如果静止,我们应当把伞放在与地面垂直的方向上。假设我们向前运动,我们会感觉雨滴不是垂直落下的,而是倾斜地迎面落下的,倾斜的角度与我们运动的速度有关,当然也与雨滴下落的速度有关,如果我们改变自己运动速度的方向和大小,雨滴下落的倾角也相应会发生变化。
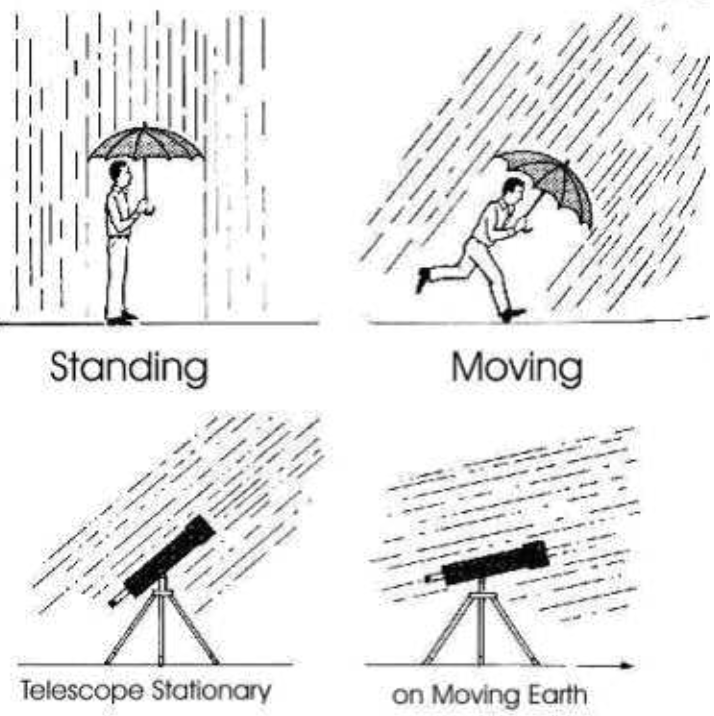
雨中行走, 雨滴下落的倾角会随行走的速度而发生变化.
如果我们承认光速是有限的,遥远恒星发出的光就好像雨滴一样从天空中落下,如果地球是运动的,那么垂直落下的星光就会变成倾斜落下的。我们知道,地球围绕太阳以大约30公里/秒的速度公转,其运动方向在不断地改变着,这意味着星光落下的方向也在不断改变,这就是所谓“光行差”。
1728年,布雷德利对天龙座星(Gamma Draconis)进行了观测,发现在6个月的时间里,它的方向改变了40秒角度,由此他可计算出光速为约31万公里/秒。布雷德利的结果不太精确,但他提供了光速是有限的独立证据。并且光行差现象本身也是导致狭义相对论产生的重要实验。
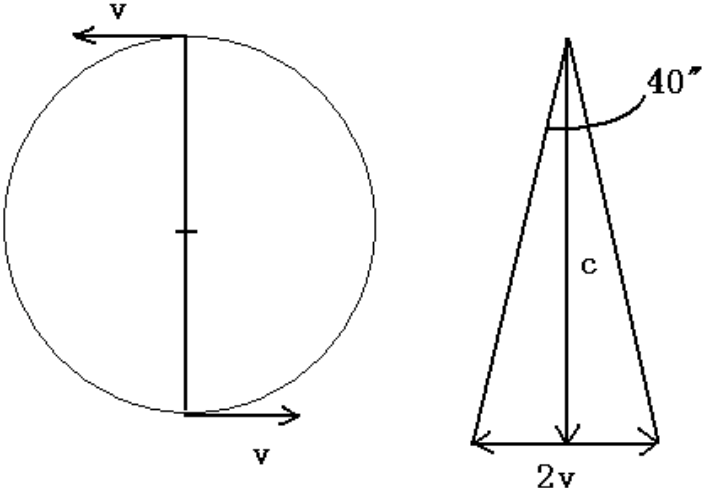
假设“光行差”用角度表示,由于很小(换算成弧度,),
由此, 可估算出:
地面测量法
直到1849年,法国物理学家斐索(Fizeau,1819-1896)才利用非天文方法在地面上第一次成功地测量了光速。斐索的仪器是非常精巧的。
斐索的方法被称为“旋转齿轮”法,它的核心是一个快速旋转的并可调整转速的齿轮,利用这个齿轮我们可以精确地测量时间。由于当时电灯尚未发明,斐索使用的光源其实是蜡烛,它发出的光波射到8公里远的镜子上并返回。假设齿轮不转动,那么蜡烛发出的光将从相邻两个齿之间穿过,然后又回来射到观察者的眼睛里。
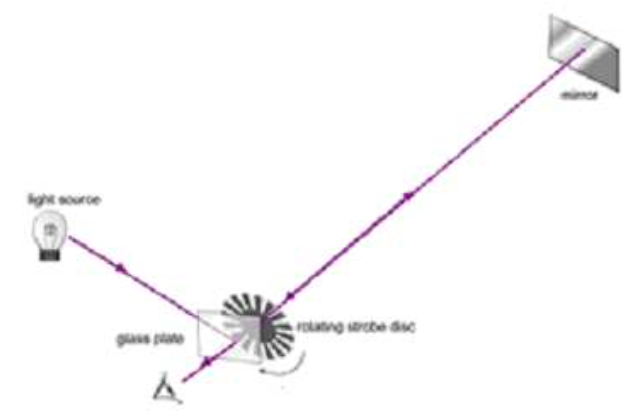
现在假设齿轮开始转动,但转速较慢,当光被镜子反射回来的时候正好被相邻的齿挡住,因此没有光射到观察者的眼睛里。如果加快齿轮的转速,使光被反射回来的时候恰好转过一个齿轮,那么光又可以射到观察者的眼睛里。于是斐索知道当齿轮恰好转过一个齿的时间,就对应的是光传播16公里所需要的时间。斐索得到的光速是313111公里/秒,考虑到他所利用仪器的局限,这个结果已经相当精确了。
1850年法国物理学家傅科(Foucault,1819-1868)利用旋转镜法首次实现了在实验室里对光速的测定。傅科使用快速旋转的镜片替代了斐索的齿轮,快速旋转的镜片会使出射光线偏转一个角度,1862年傅科的测量结果是29.8万公里/秒。
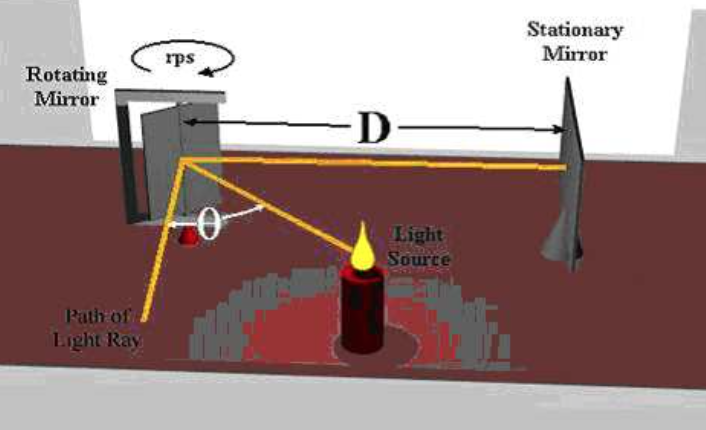
更精确的测量是由美国物理学家迈克尔逊(Michelson,1852-1931)在1926年完成的,他改进了傅科的方法,使用一个多面的旋转镜,将光波分成不连续的光束。类似于斐索的实验,这些光束将被反射到35公里远的镜子上,然后再被反射回来。如下图,我们使用一个六面镜,该镜由电动机驱动,可以任意调节旋转速度。假设镜子不转动,并且处在如图的位置,光恰好可以被观察者看到。如果多面镜旋转起来,并且旋转速度不快时,多面镜的位置将不能使光束被反射到观察者的眼睛里。但当逐渐加快多面镜旋转速度,并恰好使相邻镜面恰好处于前一个镜面原先的位置时,即多面镜转了1/6圈时,观察者将可重新看到被反射的光束。
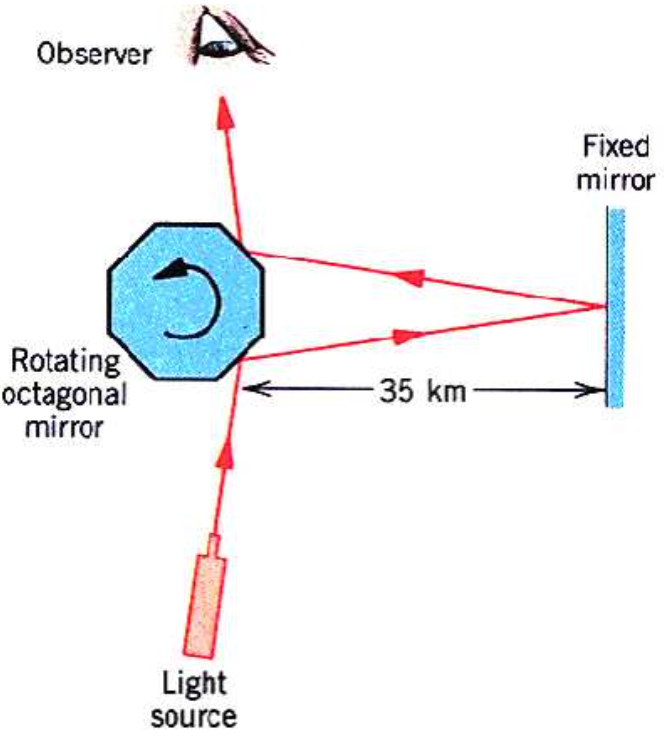
迈克尔逊在实验中使用了8面镜,12面镜和16面镜。他把旋转镜安置在加州的威尔逊山上,反射镜则安装在35公里外的圣安东尼奥山上。美国海岸与大地测量局 (Coastal and Geodetic Survey)为迈克尔逊专门精确地测量了这段距离,其误差小于5厘米。迈克尔逊1926年的测量结果是299796公里/秒,误差不超过4公里/秒。这是当时的最佳结果。
寻找以太
如果以太存在的话,它必然要弥散于整个空间,因此它应是某种凝固于宇宙中的不能运动的东西。从这个角度我们再次得到了“绝对参考系”这个概念。在哥白尼之前,地球就是这个特殊的参考系,地球是静止的,太阳和其他行星都围绕地球运动。哥白尼之后,太阳一度替代了地球的地位,被认为是静止不动的,但很快人们发现太阳本身也在围绕银河系的中心在运动。那有没有什么东西是绝对静止不动的呢?看来“以太”可以是一个潜在的选择,以太充满整个空间,它是静止不动的,其他所有物体都相对以太运动,这就是“静止以太学说”。
以太拖曳
为了便于理解,设想我们在一个巨大的湖里,湖水是静止不动的,我们坐船可以在湖水里航行,湖水就相当于静止以太。假设我们在湖水里航行,把手伸进湖水里会感觉到水在运动,换句话说我们可以通过观察水是否运动来判断船是否在运动。这就是以太漂移(ether drift)或以太风(ether wind),如果我们观察到以太风,就说明地球相对以太确实是运动的,换言之就能加强人们对以太存在的信念。
总结一下,如果采纳静止以太学说,由于地球是运动的,因此应当能观察到以太风。但可惜人们没能观察到以太风存在的效应。比如如果以太风存在,望远镜聚焦的焦点将随地球运动状况的改变而改变,但人们一直未观察到这种效应。
另一种关于以太的学说,是菲涅尔的以太拖曳学说。1818年,法国物理学家菲涅尔(Fresnel,1788-1827)提出物体内的以太密度应当比真空中的大,因此象望远镜这样的物体可拖动部分以太和它一起运动,就好像湖水中的船会拖曳部分湖水和它一起运动一样。
菲涅尔进一步定义了“拖曳系数”,拖曳系数如果为1表示以太可以完全跟上物体的运动;如果是介于0、1之间则表示以太只能部分地跟上物体的运动;为0则表示以太完全不能被拖曳,即对应静止以太。
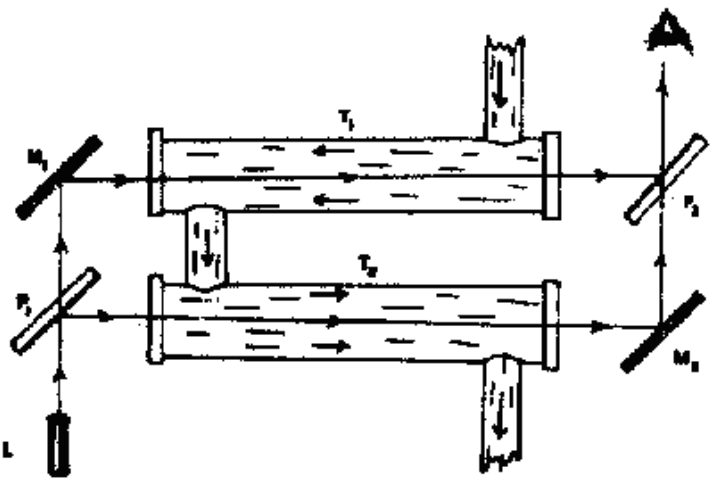
1859年,斐索做了流水实验,实验的目的是为了考察介质的运动对在其中传播的光速有何影响,从而判断以太是否被拖曳。实验装置如上图所示,光束由光源L发出后,经过半透镜后分为两束,一束光与水流方向一致,另一束光则与水流方向相反,两束光在观察者处产生干涉条纹。
斐索实验计算出以太被水拖曳的系数为0.46,而菲涅尔理论预测的系数为0.44,看起来吻合得很好。斐索实验似乎说明以太是部分被拖曳的,而这也被认为是19世纪以太学说的重要胜利。
如果以太是部分被拖曳的,以太和物体间的相对运动就是存在的,换句话说以太漂移就是存在的,但直到1879年所有试图探测以太漂移速度的实验都没有成功。1879年麦克斯韦在一封信中指出:
地面上测量光速的方法,光延同样的路径返回,所以地球相对于以太的速度对双程时间的影响取决于地球速度与光速之比的平方,这个量太小了,难以观测。
迈克尔逊---莫雷实验
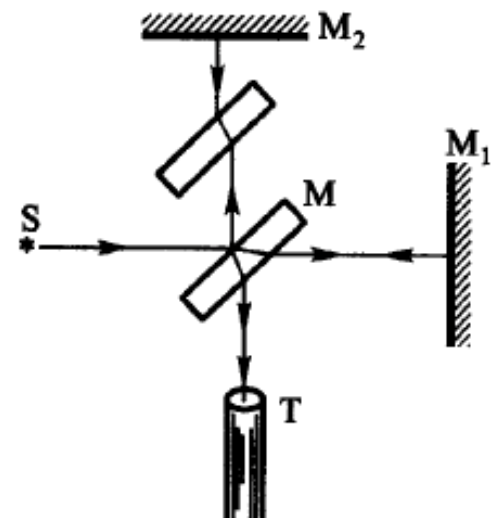
这封信恰好被迈克尔逊读到,他设计出了一种方案,利用相互垂直的两束光产生干涉的方法来比较光速的差异。上图是迈克尔逊干涉仪的原理图。假设以太风是在横向的,则横向光束传播一个来回需要用时:,而在纵向光束传播一个来回需要用时:。由此可计算出条纹移动为:。
迈克尔逊所用干涉仪的臂长是1.2米,地球围绕太阳公转的速度是30公里/秒,代入可计算出条纹移动是0.04个条纹。1881年4月迈克尔逊在德国波茨坦完成了他的实验,但他所观察到的条纹移动远远小于预期值。

迈克尔逊和莫雷在1887年在美国克里夫兰又进行了一次精度更高的实验。他们把光学仪器安装在大石板上,石板漂浮在水银槽上,可以自由地旋转方向,光路经多次反射延长为11米,预计条纹移动最大应为0.4条。但实验结果是令人失望的,他们在论文中这样写道:
从图形可以肯定,即使由于地球与以太之间的相对运动会使条纹发生位移,这种位移也不可能大于条纹间距的0.01。
迈克尔逊和莫雷在不同条件(不同季节、白天或夜晚等)下观察了很长时间,但结果始终是一致的,即未能发现地球相对于以太的任何运动。“迈克尔逊-莫雷实验”的结果是对以太部分拖曳学说的致命打击,为保留以太概念,难道以太是完全被拖曳的?但如果确实是这样,远处恒星发出的光当射到地球表面附近时,会被地球完全拖曳,如果真的这样,就不可能观察到布雷德利的光行差现象。
问题已经成熟了
各种版本的“迈克尔逊-莫雷实验”表明,以太风是不存在的,那么以太假说是否还成立呢。面对这个难题,多位物理学家给出了自己的解释。
1892年,洛仑兹发表了《论地球对以太的相对运动》,他提出物体在运动方向上收缩了,如果原长为,则收缩为,1895年,他给出了更精确的公式,。这样他就解释了为什么迈克尔逊---莫雷实验没有观测到地球相对于以太的运动。但为什么物体会发生这种收缩呢?洛仑兹给出的解释是,如果把运动物体看作是处在
静止以太中的带电粒子,它们之间的相互作用是电磁相互作用,当这些粒子运动时,所受洛仑兹力会发生改变,从而产生收缩。后来J. J. 汤姆逊发现电子,并确认原子总可分为正电部分(卢瑟福模型中发现这部分是集中分布的,称之为原子核),和负电部分(即电子)。J. J. 汤姆逊的发现是对洛仑兹理论的重要支持,自然界中的物体,包括迈克尔逊-莫雷的实验装置总可看作是以太中带电粒子的集合。
从数学的角度,洛仑兹的工作已经非常接近于后来爱因斯坦的相对论,比如洛仑兹曾得到一组变换,当物体在以太绝对静止参照系中沿轴运动时,
这个变换后来也被爱因斯坦得到了,但习惯上我们仍然称其为洛仑兹变换。洛仑兹关于运动物体的电动力学从数学形式上与爱因斯坦的狭义相对论并无区别,但他的理论是基于运动电荷的,是对麦克斯韦电动力学的发展,而与古老的运动学无关。而爱因斯坦的相对论则首先是运动学的,他推广了伽利略的惯性定律,并最终革新了我们对时空的看法。洛仑兹对迈克尔逊-莫雷实验的解释依赖于特定的物质结构假设,虽然这种物质结构后来被J. J. 汤姆逊所证实,但原则上说爱因斯坦并不需要这种物质结构假设,就能解释以太风为什么观测不到。
比较而言,法国数学家兼物理学家彭加勒则要比洛仑兹更加大胆一些。1898年,彭加勒发表了《时间的测量》,首次提出,光具有不变的速度,在一切方向上都是相同的,他把这一点看作是一条公设,并认为没有这个公设就无法测量光速。如果我们接受彭加勒的这条公设,我们自然就得到了迈克尔逊-莫雷实验的零结果。
彭加勒说:“不可能测出重物的绝对运动,或者更明确地说,不可能测出重物相对于以太的运动。人们所能提供的一切证据就是重物相对于重物的运动。”
1904年9月,彭加勒在美国的一次学术会议上,在谈到相对性原理时说:“根据这条原理,对于固定的观察者或者对于作匀速运动或平移运动的观察者来说,物理现象的定律都必然是相同的,因此,我们既没有,也不可能有任何方法判断我们是否处在匀速运动中。”(这就是伽利略的惯性定律)
彭加勒认为,伽利略的惯性定律正受到电磁学理论发展的冲击,但是惯性定律已被日常经验所证实,并“以一种不可抗拒的方式印入到人们健全的感觉中。”基于这些认识,彭加勒预言了物理学的新发展,他说:“也许我们应该建立一门崭新的力学,对这门力学我们还只能窥见它的一鳞半爪。在这门力学中,惯性随着速度增加,光速将会成为一个不可逾越的界限。”原来的比较简单的力学仍然保持为一级近似,因为它对不太大的速度还是正确的,以致在新力学中还能够发现旧力学。
正如,爱因斯坦自己所说:“要是没有我发现相对论,也会有别人发现的,问题已经成熟了。”
继续阅读
- 郭硕鸿《电动力学》,第六章
