@evilking
2018-04-30T12:56:19.000000Z
字数 16018
阅读 2929
NLP
FastText
FastText 是一种 Facebook AI Research 在 16 年开源的一个文本分类器. paper 链接: https://arxiv.org/pdf/1607.01759.pdf
其特点就是 fast,相对于其它传统的文本分类模型,如 SVM、Logistic Regression、Neural Netword 等模型,fasttext 在保持分类效果的同时,还可大大缩短训练时间和测试时间.
在原文中有说它可以将时间复杂度从 降到 ,其中 为类别数, 为文本表征向量长度;文中还说如果这种方法只考虑前 个目标,则时间复杂度可降到 .
本篇文档组织结构,前面理论部分主要是翻译 fasttext 的这篇原文,后面源码分析部分主要是在 github上找的一套源码实现再对其分析.
模型框架
该论文前面的 Introduction 部分主要是说目前很多文本分类模型虽然准确度可以,但是在大语料库上训练的很慢,于是借鉴 Word2Vec 中 CBOW 模型的思想提出了 fasttext ,可解决其他文本分类模型训练速度慢的问题.
其中 word2vec 的 CBOW 模型框架如下:
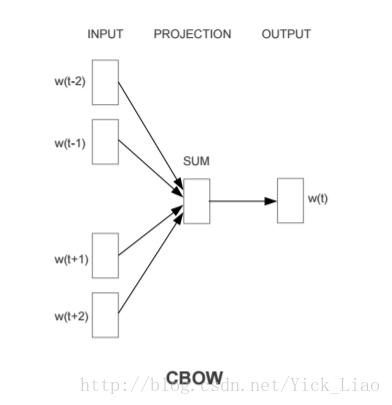
表示给定当前词 的上下文 ,来预测当前词 ,即
当然 CBOW 模型的实现又有两种: Hierarchical Softmax 和 Negative sampling. 所以 fasttext 也是有两套实现,这在后面的源码分析中我们会分别去分析.
对于句子分类来说,一个简单又有效的任务是如 BoW 模型一样用一个向量去表征句子,然后训练出线性分类器,如逻辑回归、或 SVM. 但是,线性分类器不在特征和类别中共享参数. 这可能限制了它们在大的输出空间中的泛化,在这个大的输出空间中,一些类的样本可能非常少。
常用的解决办法是将线性分类器分解成多个低秩矩阵 (Schutze, 1992; Mikolov et al., 2013),或者使用多层神经网络 (Collobert and Weston, 2008; Zhang et al., 2015).
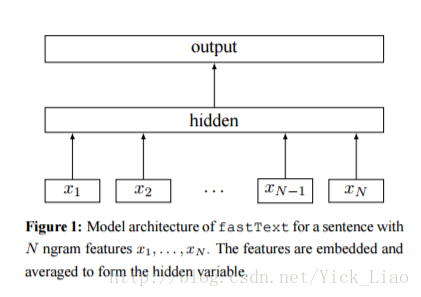
矩阵 为词典表中每个单词的词向量构成一列; 为词向量;
图中表示当前单词 的 n-gram 上下文中的单词的词向量 ,经过词向量平均后生成隐藏层向量;然后喂给线性分类器;文本表征是一个隐藏变量,有可能可以被重用.
这个模型与 Word2Vec 中 CBOW 模型框架类似,不同之处在于要预测的当前词被替换成了标签(因为是要分类). 我们使用 softmax 函数 来计算预测出各种类别的概率.
假设集合有 篇文档,使用最小化每个类别的负指数似然概率:
Hierarchical softmax
当类别数很大时,计算线性分类器在计算成本上是很昂贵的. 更进一步说,计算复杂度为 , 是类别数, 是文本表征向量的维度. 为了优化运行时间,我们使用一个基于 Huffman 编码 的 hierarchical softmax (Goodman, 2001) 树. 训练时,计算复杂度降到了 .
当查找最可能的类别时,hierarchical softmax 同样能改进测试时间. 由 Huffman 树的性质可知,每一个节点都关联一个概率,这个概率是从根节点到当前节点这条路径成立的概率. 如果当前节点的深度为 ,向上逐层回溯的父节点分别为 ,则这个概率为:
这意味着一个节点的概率总是小于它父节点的概率. 使用深度优先搜索扫描这棵树,寻找最大概率的叶子节点时,就允许我们删除任何有着较小概率的节点.
在实验中,我们观测到测试时计算复杂度减小到了 . 这个方法可更进一步扩展,使用 二叉堆 只计算前 个目标,可以将复杂度降到 .
二叉堆可参看:
https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E5%A0%86
N-gram 特征
词袋模型时丢掉了次序信息的,因为若需要精确的次序信息,在计算上是非常昂贵的. 替代方案是我们使用 n-grams 词袋模型,将 n 元词向量附加到文本特征中,在小范围内表示部分次序信息. 在实验中,这种替代方法与使用精确的次序信息 (Wang and Manning, 2012)相比,也是非常有效的.
我们通过 hashing 技巧 (Weinberger et al., 2009) 去维护一个能快速索引 n-grams 的 map 集合,其中 hash 函数与 (Mikolov et al. 2011) 中提到的一致.
翻译小结
这篇理论部分跟 Word2Vec 中 CBOW 模型类似,没什么好说的。主要在实践上,使用了一些技巧去优化性能,这点在后面源码分析中也有体现.
英文水平不行,有些地方翻译的不行,有问题及时指出一起来改进.
java 版源码分析
源码下载地址: https://github.com/ivanhk/fastText_java
加载到 eclipse 后的目录结构为:
其中 fasttext.Main 为主类,由于这套源码本身没有提供数据集进行测试,所以我们先直接跟踪源码去分析流程吧.
首先在 Main 类中的 main() 方法开始分析:
//动作命令参数String command = args[0];if ("skipgram".equalsIgnoreCase(command) || "cbow".equalsIgnoreCase(command)|| "supervised".equalsIgnoreCase(command)) {//训练模型op.train(args);} else if ("test".equalsIgnoreCase(command)) {//测试准确度op.test(args);} else if ("print-vectors".equalsIgnoreCase(command)) {op.printVectors(args);} else if ("predict".equalsIgnoreCase(command) || "predict-prob".equalsIgnoreCase(command)) {//预测类别op.predict(args);} else {printUsage();System.exit(1);}
该方法主要是通过传入的参数做不同的动作,从方法命名可知,我们主要分析的就是 op.train() 和 op.predict() 这两个功能了.
训练
模型的训练主要体现在 FastText 类的 train() 方法里,这一步之前虽然有解析传入的参数的步骤,不过我们跳过,必要时笔者会进行说明。
train() 方法的逻辑也比较清晰,前面分别去读取语料库,初始化必要的输入输出矩阵,启动模型训练线程池去真正开始训练,模型训练完成后再将模型保存到文件中。
我们一步一步来,先看语料库读取:
//设置文件读取工具类dict_.setLineReaderClass(lineReaderClass_);......//构建词典表,args.input 为输入文件的路径dict_.readFromFile(args_.input);
readFromFile(String file) 方法读取语料库,构建词典表,保存在HashMap 对象 word2int 中,这里主要是用到了上面论文中最后说的 hash 技巧.
try {long minThreshold = 1;String[] lineTokens;//循环读取每一行while ((lineTokens = lineReader.readLineTokens()) != null) {//对每行实体进行处理for (int i = 0; i <= lineTokens.length; i++) {if (i == lineTokens.length) {add(EOS);} else {if (Utils.isEmpty(lineTokens[i])) {continue;}//添加到 hash 表中add(lineTokens[i]);}//列表大小超过 75% 则重新散列,防止冲突泛滥if (size_ > 0.75 * MAX_VOCAB_SIZE) {minThreshold++;threshold(minThreshold, minThreshold);}}}} finally {if (lineReader != null) {lineReader.close();}}//重新 hash 散列,使得Map 散列均匀,优化性能threshold(args_.minCount, args_.minCountLabel);//与 word2vec 中处理高频和低频单词一样//以一定的概率过滤掉单词initTableDiscard();
这一步主要是往 HashMap 中不断添加实体(单词或者标签),当添加的量超过最大容量的 75% 时,为了提升 HashMap 的性能就需要扩容并重新 Hash 散列,这一步实现是在 threshold() 方法中。在散列的同时,会删除词频小于某一阈值的单词,还会根据实体的类别统计出单词数 nwords 和类别标签数 nlabels.
public void add(final String w) {//进行冲突检测, hash 散列long h = find(w);//进入的实体总数ntokens_++;//实体不存在 word2int 表中if (Utils.mapGetOrDefault(word2int_, h, WORDID_DEFAULT) == WORDID_DEFAULT) {entry e = new entry();e.word = w;e.count = 1;e.type = w.startsWith(args_.label) ? entry_type.label : entry_type.word;//实体列表,包括单词和类别标签words_.add(e);//size 为不同实体数 ,或者叫实体的索引word2int_.put(h, size_++);} else {//若实体存在,则词频 +1words_.get(word2int_.get(h)).count++;}}
先调用 find() 方法做冲突检查,按照 hash 散列算法进行处理的,返回不冲突的索引.
接着分析 readFromFile() 方法后面部分,主要看 initTableDiscard() 方法,后面的 args.model 参数我们是用 fasttext 做文本分类,所以模型类别为 model_name.sup,后面部分就不用看了.
public void initTableDiscard() {pdiscard_ = new ArrayList<Float>(size_);for (int i = 0; i < size_; i++) {//词频 (words是删除低频单词后的结果列表, ntokens是总共的单词数)float f = (float) (words_.get(i).count) / (float) ntokens_;pdiscard_.add((float) (Math.sqrt(args_.t / f) + args_.t / f));}}
是为了后面以一定的概率删除词频很高的词,计算公式为
接着 FastText 类的 train() 方法继续分析,初始化输入和输出矩阵:
if (!Utils.isEmpty(args_.pretrainedVectors)) {loadVectors(args_.pretrainedVectors);} else {input_ = new Matrix(dict_.nwords() + args_.bucket, args_.dim);//均匀随机分布初始化input_.uniform(1.0f / args_.dim);}//模型使用监督学习进行分类if (args_.model == model_name.sup) {output_ = new Matrix(dict_.nlabels(), args_.dim);} else {//否则就是为了构建词向量output_ = new Matrix(dict_.nwords(), args_.dim);}output_.zero();
我们先不考虑预训练的情况,直接初始化 input 矩阵,它的每行是一个单词的词向量,由均匀随机分布初始化,值的范围在 之间.
输出我们是考虑 fasttext 做监督学习预测给定文本的类别,所以 args_.model == model_name.sup,output矩阵的每一行为一个 label 的表征向量,初始值为 0 .
下面就是真正开始启动多线程去训练了.
在 TrainThread 类的 run() 方法中:
Model model = new Model(input_, output_, args_, threadId);if (args_.model == model_name.sup) {//根据损失函数不同初始化不同的结构model.setTargetCounts(dict_.getCounts(entry_type.label));} else {model.setTargetCounts(dict_.getCounts(entry_type.word));}final long ntokens = dict_.ntokens();long localTokenCount = 0;//在方法中传输的都是单词索引,可能是为了减小内存占用List<Integer> line = new ArrayList<Integer>();List<Integer> labels = new ArrayList<Integer>();String[] lineTokens;//将两重 for 循环变成了一重while (tokenCount_.get() < args_.epoch * ntokens) {lineTokens = lineReader.readLineTokens();//这样处理是为了能循环 epoch 次的训练集,//将原本要两重 for 循环的变成一重 for 循环if (lineTokens == null) {try {lineReader.rewind();} catch (Exception e) {}//到文件末尾后再重头开始读lineTokens = lineReader.readLineTokens();}//自适应学习率float progress = (float) (tokenCount_.get()) / (args_.epoch * ntokens);float lr = (float) (args_.lr * (1.0 - progress));//读取一行单词或标签到 line 和 labels localTokenCount += dict_.getLine(lineTokens, line, labels, model.rng);//走监督模型if (args_.model == model_name.sup) {dict_.addNgrams(line, args_.wordNgrams);if (labels.size() == 0 || line.size() == 0) {continue;}//这里才是走分类模型supervised(model, lr, line, labels);//后面是为了训练词向量,我们不考虑} else if (args_.model == model_name.cbow) {cbow(model, lr, line);} else if (args_.model == model_name.sg) {skipgram(model, lr, line);}}
这一步我们主要看 model.setTargetCounts() 方法和 supervised() 方法.
public void setTargetCounts(final List<Long> counts) {Utils.checkArgument(counts.size() == osz_);//负采样if (args_.loss == loss_name.ns) {initTableNegatives(counts);}//构建Huffuman树if (args_.loss == loss_name.hs) {buildTree(counts);}}
前面也说了 CBOW 模型也有两套实现方式,分别是分层的 softmax 和负采样.
我们先看 Haffman 树的实现方式,这也是论文中提到的实现.
public void buildTree(final List<Long> counts) {//每一个标签作为叶子节点,网上追溯到根节点经过的节点和 haffman 编码paths = new ArrayList<List<Integer>>(osz_);codes = new ArrayList<List<Boolean>>(osz_);//用数组的方式保存 haffman 树: tree_size = 2*num(叶子节点数) - 1tree = new ArrayList<Node>(2 * osz_ - 1);//先初始化每个节点for (int i = 0; i < 2 * osz_ - 1; i++) {Node node = new Node();node.parent = -1;node.left = -1;node.right = -1;node.count = 1000000000000000L;// 1e15f;node.binary = false;tree.add(i, node);}//tree的index 前 osz_ 存叶子节点标签for (int i = 0; i < osz_; i++) {tree.get(i).count = counts.get(i);}//从叶子节点最后往前逐步构建int leaf = osz_ - 1;int node = osz_;//首先 counts实体列表应该是按照 count 从大到小排列的顺序//从 osz 开始依次去左右两边的合成 count 较小的两个实体,然后在右边最新节点创建实体for (int i = osz_; i < 2 * osz_ - 1; i++) {int[] mini = new int[2];for (int j = 0; j < 2; j++) {if (leaf >= 0 && tree.get(leaf).count < tree.get(node).count) {mini[j] = leaf--;} else {mini[j] = node++;}}//构建父节点tree.get(i).left = mini[0];tree.get(i).right = mini[1];tree.get(i).count = tree.get(mini[0]).count + tree.get(mini[1]).count;tree.get(mini[0]).parent = i;tree.get(mini[1]).parent = i;//左侧编码为 false,右侧编码为 truetree.get(mini[1]).binary = true;} //则 tree 的最后一个节点即为根节点.//对每个叶子节点创建路由选择路径for (int i = 0; i < osz_; i++) {List<Integer> path = new ArrayList<Integer>();List<Boolean> code = new ArrayList<Boolean>();int j = i;while (tree.get(j).parent != -1) {//由 Huffman 树叶子节点的特殊性得path.add(tree.get(j).parent - osz_);code.add(tree.get(j).binary);j = tree.get(j).parent;}paths.add(path);codes.add(code);}}
上面用数组的方式来创建 Haffman 树的过程比较复杂. 首先是 counts 列表是从大到小排,依次存放在 tree 列表的前 osz 个索引位,为Haffman树的叶子节点;
然后从第 osz+1 开始往右就是存放非叶子节点。由于从 tree 列表从 0 到 osz - 1 是从大到小排,根据 Haffman 树的构造过程,不断合并 leaf 和 node 出较小的节点生成它们的父节点,并添加到 tree 的 最优边,这么递归下去,Haffman 树就构建完成了;
其中最后一个节点就是根节点.
接下来看 supervised() 方法:
public void supervised(Model model, float lr, final List<Integer> line, final List<Integer> labels) {if (labels.size() == 0 || line.size() == 0)return;//随机取一个 label 作为 line 的标号int i = Utils.randomInt(model.rng, 1, labels.size()) - 1;//line 预测 labels_imodel.update(line, labels.get(i), lr);}
如果检查到这一行有多个标签,则随机选一个.
public void update(final List<Integer> input, int target, float lr) {if (input.size() == 0) {return;}//计算隐藏层,将上下文的词向量累加computeHidden(input, hidden_);//负采样if (args_.loss == loss_name.ns) {loss_ += negativeSampling(target, lr);//分层 softmax} else if (args_.loss == loss_name.hs) {loss_ += hierarchicalSoftmax(target, lr);} else {loss_ += softmax(target, lr);}//真正用于训练的样例数nexamples_ += 1;//梯度平均分配if (args_.model == model_name.sup) {grad_.mul(1.0f / input.size());}//分别将梯度误差贡献到每个词向量上for (Integer it : input) {wi_.addRow(grad_, it, 1.0f);}}
这步跟 Word2Vec 的步骤差不多,只是预测当前词的词向量,变成了预测 label;
public void computeHidden(final List<Integer> input, Vector hidden) {Utils.checkArgument(hidden.size() == hsz_);hidden.zero();//将 wi_ 的第 it 行词向量添加到 hidden 向量上for (Integer it : input) {hidden.addRow(wi_, it);}//求个平均hidden.mul(1.0f / input.size());}
在 CBOW 模型中,隐藏层的工作就是将当前词的上下文的词向量进行累加,生成 text representation .
接下来就是将隐藏层传入输出层计算损失函数:
//负采样损失函数if (args_.loss == loss_name.ns) {loss_ += negativeSampling(target, lr);//分层 softmax损失函数} else if (args_.loss == loss_name.hs) {loss_ += hierarchicalSoftmax(target, lr);} else {loss_ += softmax(target, lr);}//真正用于训练的样例数nexamples_ += 1;//梯度平均分配if (args_.model == model_name.sup) {grad_.mul(1.0f / input.size());}//分别将梯度误差贡献到每个词向量上for (Integer it : input) {wi_.addRow(grad_, it, 1.0f);}
前面我们进行损失函数初始化时使用的 args.loss == loss_name.hs ,所以我们先只考虑 hierarchicalSoftmax() .
public float hierarchicalSoftmax(int target, float lr) {float loss = 0.0f;grad_.zero();//通过 target 索引获取路由路径final List<Boolean> binaryCode = codes.get(target);final List<Integer> pathToRoot = paths.get(target);//从叶子节点开始往上回溯,逐步逻辑回归for (int i = 0; i < pathToRoot.size(); i++) {loss += binaryLogistic(pathToRoot.get(i), binaryCode.get(i), lr);}return loss;}
hierarchical softmax 的思想就是从根节点开始,逐步做逻辑回归二分类,一层一层往下,沿着预测 label 的 路径到达预测 label 所在的叶子节点 . 其中 Haffman 树的节点的参数向量为权值向量 ,边的 code 即为分类的标号.
public float binaryLogistic(int target, boolean label, float lr) {//逻辑回归float score = sigmoid(wo_.dotRow(hidden_, target));//线性搜索误差,不过这里是不是还应该乘以sigmoid的导数: score*(1 - score) ?float alpha = lr * ((label ? 1.0f : 0.0f) - score);//更新梯度grad_.addRow(wo_, target, alpha);//更新 haffman 节点的参数向量wo_.addRow(hidden_, target, alpha);//负指数损失if (label) {//1return -log(score);} else {//0return -log(1.0f - score);}}
逻辑回归步先计算 ,然后计算 ,然后计算误差 ,接着根据 去更新梯度,然后更新 Haffman 树节点的权重向量 ;最后根据预测正例还是反例返回负指数损失.
再回到 update() 方法中,后面再将梯度误差平均分配到每个上下文词向量中.
不过上面计算 sigmoid 函数的误差的时候,笔者感觉有问题,应该是 ,根据均方误差对 求偏导算误差的公式得出.
上面是输出层的损失函数使用的 hierarchical softmax,到这里就分析完成了;下面补充 negative sampling 的流程.
先初始化负采样表:
public void initTableNegatives(final List<Long> counts) {negatives = new ArrayList<Integer>(counts.size());float z = 0.0f;//计算非规则化的词频比例for (int i = 0; i < counts.size(); i++) {z += (float) Math.pow(counts.get(i), 0.5f);}for (int i = 0; i < counts.size(); i++) {//按词频做权重剖分 负采用表大小float c = (float) Math.pow(counts.get(i), 0.5f);//等距剖分,距离为 1for (int j = 0; j < c * NEGATIVE_TABLE_SIZE / z; j++) {negatives.add(i);}}//列表混洗Utils.shuffle(negatives, rng);}
负采样逻辑与 Word2Vec 一样,先根据每个单词的词频算占总体的权重,然后对 NEGATIVE_TABLE_SIZE 长度进行等距剖分,从代码中可以看到,变量 j 每次加 1,说明等距剖分的距离为 1;然后进行混洗,方便后续随机采样.
具体可参看: http://blog.csdn.net/itplus/article/details/37999613
再看训练时的损失函数部分:
public float negativeSampling(int target, float lr) {float loss = 0.0f;grad_.zero();// args.neg 为采样次数for (int n = 0; n <= args_.neg; n++) {if (n == 0) {//第一个是正例loss += binaryLogistic(target, true, lr);} else {//其他是反例loss += binaryLogistic(getNegative(target), false, lr);}}return loss;}
负采样使用的思路是:预测当前词为正例样本,预测其他词为负例样本,多次采样,循环做逻辑回归. 具体可参看 Word2Vec 的负采样版本: https://www.zybuluo.com/evilking/note/871932;区别在于 Word2Vec 中是预测当前词,而 FastText 是根据当前词的上下文预测 label .
代码逻辑如注释所述,而逻辑回归部分在前面以及分析了,这里就不讲。重点是如何采样?
public int getNegative(int target) {int negative;do {//从采样表里采样negative = negatives.get(negpos);//每次 +1 遍历negpos = (negpos + 1) % negatives.size();//若采样到 target 就跳过重新采样} while (target == negative);return negative;}
到这里训练部分就分析完了,代码的整个流程都还是挺清晰的.
预测
模型训练完成后就可用于预测,给定一个文本,可以预测其标签。
回到 Main 类的 predict() 方法:
//加载模型FastText fasttext = new FastText();fasttext.loadModel(args[1]);//预测文本fasttext.predict(new FileInputStream(file), k, print_prob);
注意这里的参数 k ,在论文中提到,当只考虑前 个目标时,计算复杂度可降到 ,这里的 k 即 ,这是为了进一步提高速度.
我们沿着:
fasttext.predict() ——> predict(lineTokens,k) ——> model.predict():
Model 类中:
public void predict(final List<Integer> input, int k, List<Pair<Float, Integer>> heap) {predict(input, k, heap, hidden_, output_);}
对这里的参数进行说明:
input为输入一行文本,分词后每个单词在词典表中的索引,构成的索引列表.k为取前 个最大可能概率的预测类别.heap用来存前k个 (label,prob)hidden_为训练好的 fasttext 模型的 softmax 权值矩阵.output_暂时为空,供后面逻辑使用.
public void predict(final List<Integer> input, int k, List<Pair<Float, Integer>> heap, Vector hidden,Vector output) {//将上下文词向量累加computeHidden(input, hidden);if (args_.loss == loss_name.hs) {//深度优先搜索dfs(k, 2 * osz_ - 2, 0.0f, heap, hidden);} else {//直接找最好的 k 个findKBest(k, heap, hidden, output);}//重新从大到小排序Collections.sort(heap, comparePairs);}
第一步计算 将当前词的上下文词向量进行累加.
针对不同的损失函数,预测这里有不同的方法,先看若输出层为 hierarchical softmax 时如何预测:
public void dfs(int k, int node, float score, List<Pair<Float, Integer>> heap, Vector hidden) {//如果 heap 存 k 个已经满了,而当前计算的score比heap 中最小的节点概率还小,可直接过滤不考虑if (heap.size() == k && score < heap.get(heap.size() - 1).getKey()) {return;}//当 node 为叶子节点时if (tree.get(node).left == -1 && tree.get(node).right == -1) {//添加进 heap 中heap.add(new Pair<Float, Integer>(score, node));//将 heap 重新由大到小排序Collections.sort(heap, comparePairs);//如果这时 heap 的大小大于 k 了,就移除概率最小的那个节点if (heap.size() > k) {Collections.sort(heap, comparePairs);heap.remove(heap.size() - 1); // pop last}return;}//逻辑回归算分为正例的概率float f = sigmoid(wo_.dotRow(hidden, node - osz_));//递归左侧路径,分为负例dfs(k, tree.get(node).left, score + log(1.0f - f), heap, hidden);//递归右侧路径,分为正例dfs(k, tree.get(node).right, score + log(f), heap, hidden);}
这里依然是取前 k 个路径概率最大的节点,用到了 Haffman 树的特性: 子节点的路径概率肯定小于父节点的路径概率,如果父节点由于路径概率过小而被剔除,那子节点更加不用考虑.
对于输出层为负采样损失函数来说复杂度就高点:
public void findKBest(int k, List<Pair<Float, Integer>> heap, Vector hidden, Vector output) {//分别计算预测到所有类别的概率,并用softmax规则化computeOutputSoftmax(hidden, output);//遍历所有类别,取前 k 个最大概率的节点for (int i = 0; i < osz_; i++) {if (heap.size() == k && log(output.get(i)) < heap.get(heap.size() - 1).getKey()) {continue;}heap.add(new Pair<Float, Integer>(log(output.get(i)), i));Collections.sort(heap, comparePairs);if (heap.size() > k) {Collections.sort(heap, comparePairs);// pop lastheap.remove(heap.size() - 1);}}}
这个方法主要是 computeOutputSoftmax(hidden, output) 这句,后面是为了遍历所有类别,取前 k 个预测类别的概率最大的节点,代码都好理解.
public void computeOutputSoftmax(Vector hidden, Vector output) {//矩阵运算,每个类别的权值向量与文本表示成绩output.mul(wo_, hidden);//计算最大的 X^T * thetafloat max = output.get(0), z = 0.0f;for (int i = 1; i < osz_; i++) {max = Math.max(output.get(i), max);}//softmax 规则化for (int i = 0; i < osz_; i++) {output.set(i, (float) Math.exp(output.get(i) - max));z += output.get(i);}for (int i = 0; i < osz_; i++) {output.set(i, output.get(i) / z);}}
第一步根据矩阵乘法,计算出所有类别的输出层输入概率,即 ,然后做 softmax 规则化,使用的公式如下:
其中 笔者以为是为了做数据标准化,但是又不对,如果按最大最小标准化的话应该是 ,如果 softmax 的分母将 给提出来的话,代码中的公式就是对的了.
小结
本篇上半部分主要是翻译 FastText 的原论文,在该论文中也没怎么说具体的操作步骤,因为 fasttext 的模型框架与 Word2Vec 中 CBOW 模型类似,只是将预测词向量变成了预测 label 向量,而其他技巧主要是编程实现上做了改进.
所以在下半部分源码分析中做了说明,而源码分析笔者也只能带领读者梳理下分析流程,具体源码中的用意还需要读者自己多理解.
希望能对读者理解 fasttext 有所帮助,谢谢!
