NLP

Word2Vec之 基于Hierarchical Softmax的模型

基于 Hierarchical Softmax 的模型

CBOW 模型

网络结构

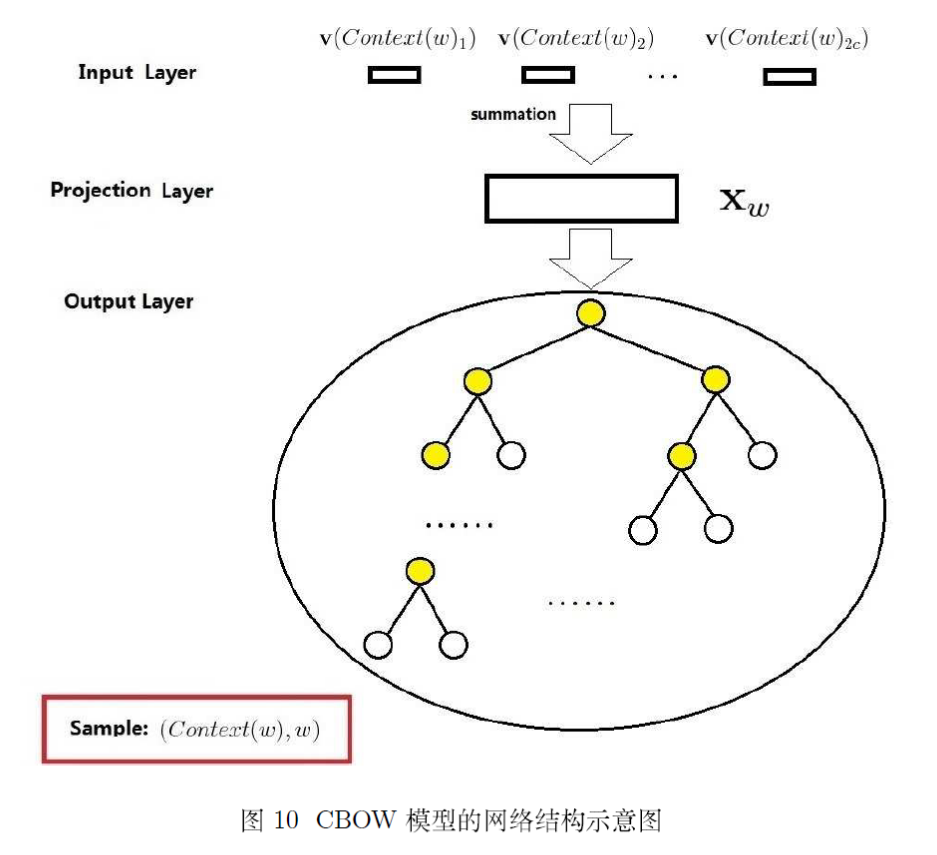
上图给出了 CBOW 模型的网络结构，它包括三层: 输入层、投影层和输出层.下面以样本 $(Context(\omega),\omega)$ 为例对这三层做说明.

• 输入层: 包含 $Context(\omega)$ 中 $2c$ 个词的词向量 $V(Context(\omega)_1),V(Context(\omega)_2),\cdots,V(Context(\omega)_{2c}) \in R^m$. 这里 m 表示词向量的长度.

• 投影层: 将输入层的 $2c$ 个向量做求和累加，即 $X_{\omega} = \sum_{i=1}^{2c}{V(Context(\omega)_i)} \in R^m$

• 输出层: 输出层对应一棵二叉树，它是以语料中出现过的词当叶子结点，以各词在语料中出现的词频当权重构造出来的 Huffman树.在这颗 Huffman树中，叶子结点共 $N( = |D|)$个，分别对应词典 $D$ 中的词，非叶子结点 $N - 1$ 个.

总结一下，对比神经概率语言模型的网络图和CBOW模型的结构图，可知道:

• （从输入层到投影层的操作）前者是通过拼接，后者通过累加求和.

• （隐藏层）前者有隐藏层，后者无隐藏层.

• （输出层）前者是线性结构，后者是树形结构.

在介绍神经概率语言模型时我们可知，模型的大部分计算集中在神经网络的隐藏层和输出层之间的矩阵向量运算，以及输出层上的 softmax 归一化运算.

而从上面的对比中可见，CBOW 模型对这些复杂度高的地方有针对性的进行了改变，首先去掉了隐藏层，其次输出层改用了 Huffman树，从而为利用 Hierarchical softmax 技术奠定了基础.

---

梯度计算

为下面讨论方便，我们先引入若干相关记号.考虑 Huffman 树种的某个叶子结点，假设它对应词典 $D$中的词 $\omega$，记

• $p^{\omega}$：从根结点出发到达 $\omega$ 对应叶子结点的路径

• $l^{\omega}$：路径 $p^{\omega}$ 中包含结点的个数

• $p_1^{\omega},p_2^{\omega},\cdots,p_{l^{\omega}}^{\omega}$：路径 $p^{\omega}$ 中的 $l^{\omega}$ 个结点，其中 $p_1^{\omega}$ 表示根结点，$p_{l^{\omega}}^{\omega}$表示词 $\omega$ 对应的结点

• $d_2^{\omega},d_3^{\omega},\cdots,d_{l^{\omega}}^{\omega} \in \{0,1\}$：词 $\omega$ 的 Huffman编码，它由 $l^{\omega} - 1$ 位编码构成，$d_j^{\omega}$ 表示路径 $p^{\omega}$ 中第 j 个结点对应的编码（根结点不对应编码）

• $\theta_1^{\omega},\theta_2^{\omega},\cdots,\theta_{l^{\omega} - 1}^{\omega} \in R^m$：路径 $p^{\omega}$ 中非叶子结点对应的向量，$\theta_j^{\omega}$ 表示路径 $p^{\omega}$ 中第 j 个非叶子结点对应的向量

下面以一个简单的例子来进一步说明一下：

句子为“我喜欢观看巴西足球世界杯”，分词后为“我 喜欢 观看 巴西 足球 世界杯”，假设根据语料库，分别统计分词后的各个词的频率，构建Huffman树如下图所示:

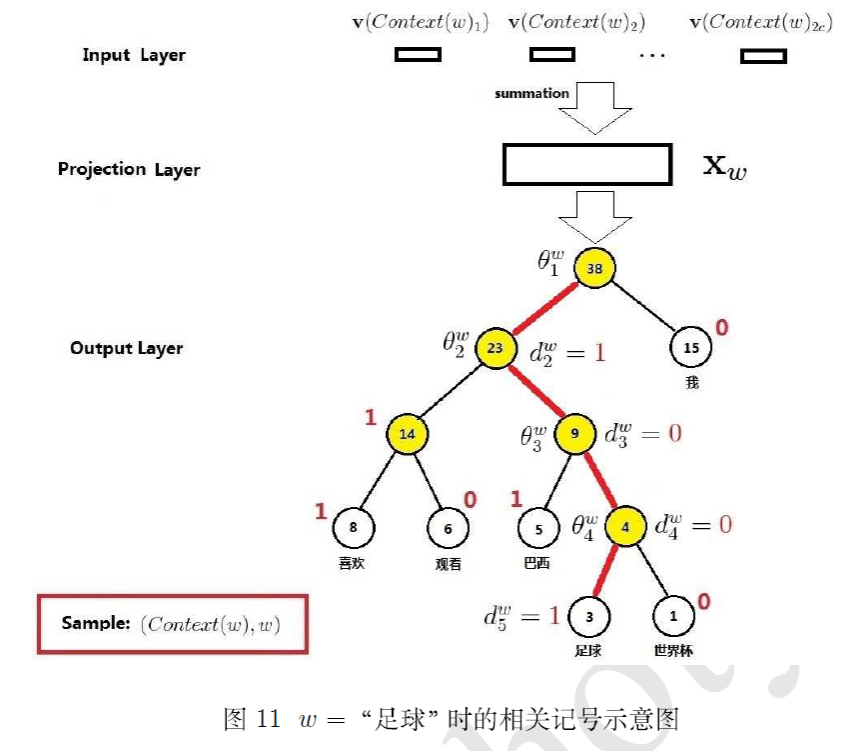
考虑词 $\omega$ = "足球"的情形，图中由 44 条红色边串起来的 5 个结点就构成路径 $p^{\omega}$，其长度 $l^{\omega} = 5$. $p_1^{\omega},p_2^{\omega},p_3^{\omega},p_4^{\omega},p_5^{\omega}$ 为路径 $p^{\omega}$ 上的 5 个结点，其中 $p_1^{\omega}$ 对应根结点. $d_2^{\omega},d_3^{\omega},d_4^{\omega},d_5^{\omega}$ 分别为 $1,0,0,1$，即"足球"的 Huffman编码为 1001.此外 $\theta_1^{\omega},\theta_2^{\omega},\theta_3^{\omega},\theta_4^{\omega}$ 分别表示路径 $p^{\omega}$ 上 4 个非叶子结点对应的向量.

---

那么在 CBOW 模型的网络结构下，如何定义条件概率函数 $p(\omega | Context(\omega))$呢？更具体地说，就是如何利用向量 $X_{\omega} \in R^m$ 以及 Huffman 树来定义函数 $p(\omega | Context(\omega))$呢？

考虑上面的"足球"的例子，从根节点出发到达"足球"这个叶子结点，中间共经历了 4 次分支（每条红色的边对应一次分支），而每一次分支都可视为进行一次二分类.

既然是从二分类的角度来考虑问题，那么对于每一个非叶子结点，就需要为其左右孩子结点指定一个类别，即哪个是正类（标签为 1），哪个是负类（标签为 0）.碰巧，除根结点以外，树中每个结点都对应了一个取值为 0 或 1 的 Huffman编码.因此一种最自然的做法就是将 Huffman编码为 1 的结点定义为正类，而将编码为 0 的结点定义为负类.当然，这只是一个约定，你也可以调过来，0 表示正类，1 表示负类.为了与word2vec中的定义保存一致，我们统一约定为：一个结点进行分类时，分到左边就是负类，编码为 1，分到右边就是正类，编码为 0.

逻辑回归中我们知道，一个结点被分为正类的概率是

$$\sigma(X_{\omega}^T \theta) = \frac{1}{1 + e^{-X_{\omega}^T \theta}}$$ 被分为负类的概率当然就等于 $$1 - \sigma(X_{\omega}^T \theta)$$

注意，上式中有个 $\theta$ 的向量，它是待定参数，显然在这里非叶子结点对应的那些向量 $\theta_i^{\omega}$ 就可以扮演参数 $\theta$ 的角色

对于词典 $D$ 中的任意词 $\omega$，Huffman 树中一定存在一条从根结点到词 $\omega$ 对应结点的路径 $p^{\omega}$（且这条路径是唯一的）.路径 $p^{\omega}$ 上存在 $l^{\omega} - 1$ 个分支，将每个分支看做一次二分类，每一次分类就产生一个概率，将这些概率乘起来，就是我们所需要的 $p(\omega | Context(\omega))$.

那么条件概率 $p(\omega | Context(\omega))$ 的一般公式可写为:

$$p(\omega | Context(\omega)) = \prod_{j=2}^{l^{\omega}}{p(d_j^{\omega} | X_{\omega},\theta_{j-1}^{\omega})}$$ 其中: $$p(d_j^{\omega} | X_{\omega},\theta_{j-1}^{\omega}) = \begin{cases} \sigma(X_{\omega}^T \theta_{j-1}^{\omega}), d_j^{\omega} = 0; \\ 1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega}), d_j^{\omega} = 1; \end{cases}$$
或者写成整体表达式： $$p(d_j^{\omega} | X_{\omega},\theta_{j-1}^{\omega}) = \left[ \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \right]^{1 - d_j^{\omega}} \cdot \left[ 1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \right]^{d_j^{\omega}}$$

将上式代入到对数似然函数中，便可得到:

$$L = \sum_{\omega \in C}{log{\prod_{j=2}^{l^{\omega}}{\{\left[ \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \right]^{1 - d_j^{\omega}} \cdot \left[ 1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \right]^{d_j^{\omega}}\}}}} \\ = \sum_{\omega \in C} \sum_{j=2}^{l^{\omega}}{\{(1 - d_j^{\omega}) \cdot log[\sigma(X_{\omega}^T \theta_{j-1}^{\omega})] + d_j^{\omega} \cdot log[1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})] \}}$$
为了下面讨论方便，我们假定: $$L(\omega,j) = (1 - d_j^{\omega}) \cdot log[\sigma(X_{\omega}^T \theta_{j-1}^{\omega})] + d_j^{\omega} \cdot log[1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})]$$
到这里我们已经推导出对数似然函数 $L$，这就是 CBOW 模型的目标函数，下面考虑如何最大化目标函数，word2vec 里面采用的是 随机梯度上升法，而梯度类算法的关键是给出相应的梯度计算公式，因此接下来重点讨论梯度的计算.

---

随机梯度上升法的做法是：每取一个样本 $(Context(\omega),\omega)$，就对目标函数中的所有（相关）参数做一次刷新.

从目标函数的公式可以看出，核心的是 $L(\omega,j)$ 函数，只需要对这个函数进行最大化就可以实现对目标函数最大化了；该函数中的参数包括向量 $X_{\omega},\theta_{j-1}^{\omega},\omega \in C,j = 2,\cdots,l^{\omega}$.为此，先给出函数 $L(\omega,j)$关于这些向量的梯度.

首先考虑 $L(\omega,j)$ 关于 $\theta_{j-1}^{\omega}$ 的梯度计算:

$$\frac{\partial L(\omega,j)}{\partial \theta_{j-1}^{\omega}} = \frac{\partial}{\partial \theta_{j-1}^{\omega}}{\{ (1 - d_j^{\omega}) \cdot log[\sigma(X_{\omega}^T \theta_{j-1}^{\omega})] + d_j^{\omega} \cdot log[1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})] \}} \\= (1-d_j^{\omega}) \cdot \frac{1}{\sigma(X_{\omega}^T \theta_{j-1}^{\omega})} \cdot [ \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \cdot ( 1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})) ]X_{\omega} - d_j^{\omega} \cdot \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \cdot X_{\omega} \\= \{ (1 - d_j^{\omega})[1 - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})] - d_j^{\omega} \sigma(X_{\omega}^T \theta_{j-1}^{\omega}) \}X_{\omega} \\= [1 - d_j^{\omega} - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})]X_{\omega}$$
于是，$\theta_{j-1}^{\omega}$ 的更新公式可写为: $$\theta_{j-1}^{\omega} := \theta_{j-1}^{\omega} + \eta [1 - d_j^{\omega} - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})]X_{\omega}$$ 其中 $\eta$ 表示学习率.

---

然后考虑 $L(\omega,j)$ 关于 $X_{\omega}$ 的梯度，同样按类似于上面的步骤，可求得

$$\frac{\partial L(\omega,j)}{\partial X_{\omega}} = [1 - d_j^{\omega} - \sigma(X_{\omega}^T \theta_{j-1}^{\omega})] \theta_{j-1}^{\omega}$$
这里有个问题，我们的最终目的是要求词典 $D$ 中每个词的词向量，而这里的 $X_{\omega}$ 表示的是 $Context(\omega)$ 中各词词向量的累加.那么如何利用 $\frac{\partial L(\omega,j)}{\partial X_{\omega}}$来对 $V(\overline{\omega}),\overline{\omega} \in Context(\omega)$ 进行更新呢？word2vec 中的做法很简单，直接取 $$V(\overline{\omega}) := V(\overline{\omega}) + \eta \sum_{j=2}^{l^{\omega}}{\frac{\partial L(\omega,j)}{\partial X_{\omega}}}, \overline{\omega} \in Context(\omega)$$ 即把 $\sum_{j=2}^{l^{\omega}}{\frac{\partial L(\omega,j)}{\partial X_{\omega}}}$ 贡献到 $Context(\omega)$ 中每一个词的词向量上，这点就很好理解了，既然 $X_{\omega}$ 本身就是 $Context(\omega)$ 中各词词向量的累加，求完梯度后当然要将其反向传播到每个分量上去.

---

下面以样本 $(Context(\omega),\omega)$ 为例，给出 CBOW 模型中采用随机梯度上升法更新各参数的伪代码:

1. $e = 0$
2. $X_{\omega} = \sum_{\mu \in Context(\omega)} V(\mu)$
3. $for \ j = 2;l^{\omega} \ do$
   $\{$
   $\ \ \ \ q = \sigma(X_{\omega}^T \theta_{j-1}^{\omega})$
   $\ \ \ \ g = \eta(1 - d_j^{\omega} - q)$
   $\ \ \ \ e := e + g \cdot \theta_{j-1}^{\omega}$
   $\ \ \ \ \theta_{j-1}^{\omega} := \theta_{j-1}^{\omega} + g \cdot X_{\omega}$
   $\}$
4. $for \ \mu \in Context(\omega) \ do$
   $\{$
   $\ \ \ \ V(\mu) := V(\mu) + e$
   $\}$

---

Skip-gram 模型

skip-gram 模型与 cbow 模型的推导过程大同小异，所以推导过程中的记号保持含义一致.

网络结构

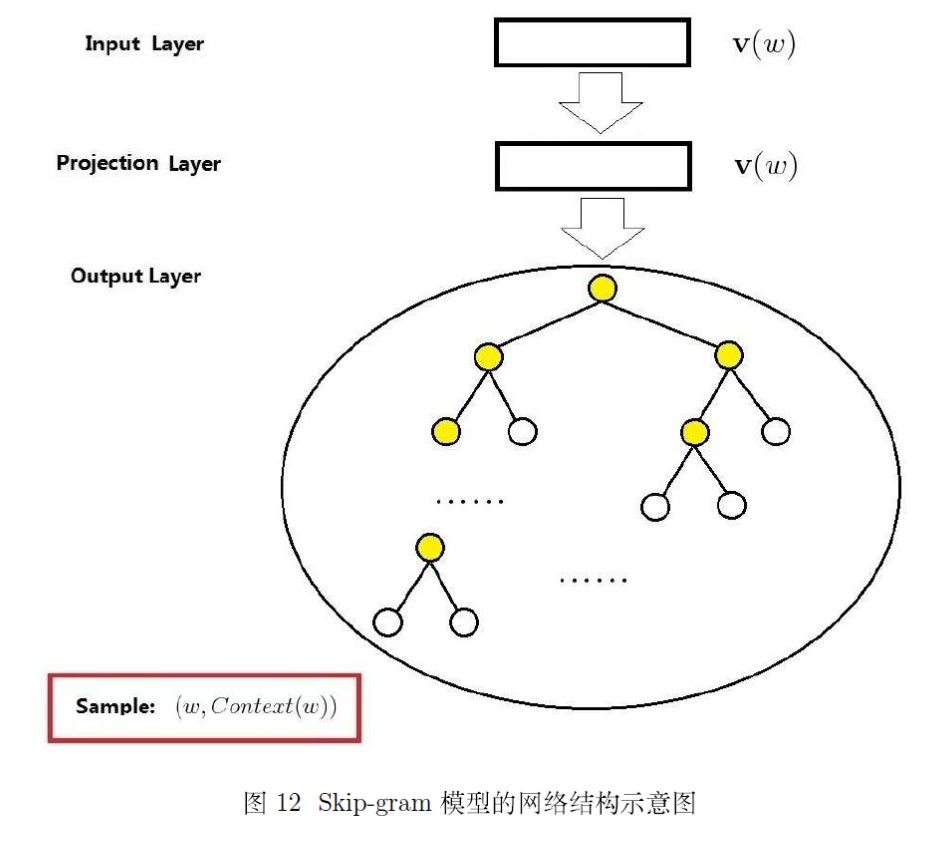
同 CBOW 模型的网络结构一样，这里给出三层结构的说明：

1. 输入层：只含当前样本的中心词 $\omega$ 的词向量 $V(\omega) \in R^m$

2. 投影层：这是个恒等投影，把 $V(\omega)$ 投影到 $V(\omega)$.因此，这个投影层其实是多余的；这里之所以保留投影层主要是方便和 CBOW模型的网络结构做对比

3. 输出层：和 CBOW 模型一样，输出层也是一棵 Huffman树

---

梯度计算

对于 Skip-gram 模型，已知的是当前词 $\omega$，需要对其上下文 $Context(\omega)$ 中的词进行预测，则可将 Skip-gram 模型中的条件概率函数 $p(Context(\omega) | \omega)$定义为:

$$p(Context(\omega) | \omega) = \prod_{\mu \in Context(\omega)} p(\mu | \omega)$$ 其中，$p(\mu | \omega)$ 可按照 Hierarchical Softmax 思想，类似的写为: $$p(\mu | \omega) = \prod_{j=2}^{l^{\mu}} p(d_j^{\mu} | V(\omega),\theta_{j-1}^{\mu})$$ 其中 $$p(d_j^{\mu} | V(\omega),\theta_{j-1}^{\mu}) = [ \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ]^{1 - d_j^{\mu}} \cdot [ 1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ]^{d_j^{\mu}}$$

将上式依次代回，可得对数似然函数的具体表达式为:

$$L = \sum_{\omega \in C} log{\prod_{\mu \in Context(\omega)} \prod_{j=2}^{l^{\mu}} \{ [\sigma(V(\omega)^T \theta_{j-1}^{\mu})]^{1 - d_j^{\mu}} \cdot [1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ]^{d_j^{\mu}} \} } \\= \sum_{\omega \in C} \sum_{\mu \in Context(\omega)} \sum_{j=2}^{l^{\mu}} \{ (1 - d_j^{\mu}) \cdot log[\sigma(V(\omega)^T \theta_{j-1}^{\mu})] + d_j^{\mu} \cdot log[1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ] \}$$
同样，为下面梯度推导方便起见，将三重求和符号下花括号里的内容简记为 $L(\omega,\mu,j)$，即 $$L(\omega,\mu,j) = (1 - d_j^{\mu}) \cdot log[\sigma(V(\omega)^T \theta_{j-1}^{\mu})] + d_j^{\mu} \cdot log[1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ]$$
至此，已经推导出对数似然函数的表达式，这就是 Skip-gram 模型的目标函数.接下来同样利用 随机梯度上升法 对其进行优化.

---

首先考虑 $L(\omega,\mu,j)$ 关于 $\theta_{j-1}^{\mu}$ 的梯度计算（与 CBOW模型 对应部分的推导完全类似 ）.

$$\frac{\partial L(\omega,\mu,j)}{\partial \theta_{j-1}^{\mu}} = \frac{\partial}{\partial \theta_{j-1}^{\mu}} \{ (1 - d_j^{\mu}) \cdot log[\sigma(V(\omega)^T \theta_{j-1}^{\mu})] + d_j^{\mu} \cdot log[1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ] \} \\= (1 - d_j^{\mu})[ 1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ]V(\omega) - d_j^{\mu} \sigma(V(\omega)^T \theta_{j-1}^{\mu}) V(\omega) \\= \{ (1 - d_j^{\mu})[ 1 - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ] - d_j^{\mu} \sigma(V(\omega)^T \theta_{j-1}^{\mu}) \} V(\omega)$$
于是，$\theta_{j-1}^{\mu}$ 的更新公式可写为:
$$\theta_{j-1}^{\mu} := \theta_{j-1}^{\mu} + \eta [1 - d_j^{\mu} - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ] V(\omega)$$
接下来考虑 $L(\omega,\mu,j)$ 关于 $V(\omega)$ 的梯度.同样利用 $L(\omega,\mu,j)$中 $V(\omega)$ 和 $\theta_{j-1}^{\omega}$ 的对称性，有 $$\frac{L(\omega,\mu,j)}{V(\omega)} = [1 - d_j^{\mu} - \sigma(V(\omega)^T \theta_{j-1}^{\mu}) ] \theta_{j-1}^{\mu}$$ 于是，$V(\omega)$ 的更新公式可写为: $$V(\omega) := V(\omega) + \eta \sum_{\mu \in Context(\omega)} \sum_{j=2}^{l^{\mu}} \frac{\partial L(\omega,\mu,j)}{\partial V(\omega)}$$
下面以样本 $(\omega,Context(\omega))$ 为例，给出 Skip-gram 模型中采用随机梯度上升法更新参数的伪代码:

1. $\boldsymbol{e} = 0$
2. $for \ \ \mu \in Context(\omega) \ \ do$
3. $\{$
4. $\ \ \ \ for \ \ j = 2 : l^{\mu} \ \ do$
5. $\ \ \ \ \{$
6. $\ \ \ \ \ \ \ \ q = \sigma(V(\omega)^T \theta_{j-1}^{\mu})$
7. $\ \ \ \ \ \ \ \ g = \eta (1 - d_j^{\mu} - q)$
8. $\ \ \ \ \ \ \ \ \boldsymbol{e} := \boldsymbol{e} + g \theta_{j-1}^{\mu}$
9. $\ \ \ \ \ \ \ \ \theta_{j-1}^{\mu} := \theta_{j-1}^{\mu} + g V(\omega)$
10. $\ \ \ \ \}$
11. $\}$
12. $V(\omega) := V(\omega) + \boldsymbol{e}$

但是，word2vec源码中，并不是等 $Context(\omega)$ 中的所有词都处理完后才刷新 $V(\omega)$，而是每处理完 $Context(\omega)$ 中的一个词 $\mu$，就及时刷新一次 $V(\omega)$，具体为:

1. $for \ \ \mu \in Context(\omega) \ \ do$
2. $\{$
3. $\ \ \ \ \boldsymbol{e} = 0$
4. $\ \ \ \ for \ \ j = 2 : l^{\mu} \ \ do$
5. $\ \ \ \ \{$
6. $\ \ \ \ \ \ \ \ q = \sigma(V(\omega)^T \theta_{j-1}^{\mu})$
7. $\ \ \ \ \ \ \ \ g = \eta (1 - d_j^{\mu} - q)$
8. $\ \ \ \ \ \ \ \ \boldsymbol{e} := \boldsymbol{e} + g \theta_{j-1}^{\mu}$
9. $\ \ \ \ \ \ \ \ \theta_{j-1}^{\mu} := \theta_{j-1}^{\mu} + g V(\omega)$
10. $\ \ \ \ \}$
11. $\ \ \ \ V(\omega) := V(\omega) + \boldsymbol{e}$
12. $\}$

同样，需要注意的是，循环体内的步 8 和 步 9 不能交换次序，即 $\theta_{j-1}^{\mu}$ 要等贡献到 $\boldsymbol{e}$ 后才更新.