时间序列篇

ARIMA模型

前面的篇幅中我们讲解了 $ARMA$ 模型，而差分运算具有强大的确定性信息提取能力，许多非平稳序列差分后会显示出平稳序列的性质，这时我们称这个非平稳序列为差分平稳序列.对差分平稳序列可以使用 $ARIMA$ 模型进行拟合.

$ARIMA$ 模型的结构

具有如下结构的模型称为求和自回归移动平均模型，简记为 $ARIMA(p,d,q)$ 模型:

$$\begin{cases} \Phi(B)\nabla^d x_t = \Theta(B) \epsilon_t \\ E(\epsilon_t) = 0, Var(\epsilon_t) = \sigma_{\epsilon}^2 , E(\epsilon_t \epsilon_s) = 0, s \neq t \\ E(x_s \epsilon_t) = 0, \forall s < t \end{cases}$$ 式中，$\nabla^d = (1 - B)^d; \Phi(B) = 1 - \phi_1 B - \cdots - \phi_p B^p$，为平稳可逆 $ARMA(p,q)$ 模型的自回归系数多项式；$\Theta(B) = 1 - \theta_1 B - \cdots - \theta_q B^q$，为平稳可逆 $ARMA(p,q)$ 模型的移动平滑系数多项式.

求和自回归移动平均模型这个名字的由来是因为 $d$ 阶差分后序列可以表示为:

$$\nabla^d x_t = \sum_{i = 0}^d{(-1)^i C_d^i x_{t-i}}$$ 式中，$C_d^i = \frac{d!}{i! (d-i)!}$ ，即差分后序列等于原序列的若干序列值的加权和，而对它又可以拟合自回归移动平均($ARMA$)模型，所以称它为求和自回归移动平均模型.

另有:

$$\nabla^d x_t = \frac{\Theta(B)}{\Phi(B)}$$ 式中，$\{\epsilon_t\}$ 为零均值白噪声序列.

---

由上式容易看出，$ARIMA$ 模型的实质就是差分运算与 $ARMA$ 模型的组合.这说明任何非平稳序列如果能够通过适当阶数的差分实现差分后平稳，就可以对差分后序列进行 $ARMA$ 模型拟合了.而 $ARMA$ 模型的分析方法非常成熟，这意味着对差分平稳序列的分析也将是非常简单、非常可靠的.

特别的：

• 当 $d=0$ 时，$ARIMA(p,d,q)$模型实际上就是 $ARMA(p,q)$ 模型.

• 当 $p = 0$ 时，$ARIMA(0,d,q)$模型可以简记为 $IMA(d,q)$ 模型.

• 当 $q = 0$ 时，$ARIMA(p,d,0)$ 模型可以简记为 $ARI(p,d)$ 模型.

• 当 $d = 1,p = q = 0$ 时，$ARIMA(0,1,0)$模型为:

  $$\begin{cases} x_t = x_{t-1} + \epsilon_t \\ E(\epsilon_t) = 0,Var(\epsilon_t) = \sigma_{\epsilon}^2, E(\epsilon_t \epsilon_s) = 0, s \neq t \\ E(x_s \epsilon_t) = 0, \forall s < t \end{cases}$$
  该模型称为随机游走(random walk)模型，或醉汉模型.

随机游走模型描述为：假如有个醉汉醉得非常严重，完全丧失方向感，把他放在荒郊野外，一段时间之后再去找他，在什么地方找到他的概率最大呢?

---

$ARIMA$模型的性质

平稳性

假如 $\{x_t\}$ 服从 $ARIMA(p,d,q)$ 模型:

$$\Phi(B) \nabla^d x_t = \Theta(B) \epsilon_t$$
式中， $$\nabla^d = (1-B)^d \\ \Phi(B) = 1 - \phi_1 B - \cdots - \phi_p B^p \\ \Theta(B) = 1 - \theta_1 B - \cdots - \theta_q B^q$$ 记 $\varphi(B) = \Phi(B) \nabla^d$，$\varphi(B)$ 称为广义自回归系数多项式.显然 $ARIMA$ 模型的平稳性完全由 $\varphi(B) = 0$的根的性质决定.

因为 $\{x_t\}d阶$差分后平稳，服从 $ARMA(p,q)$模型，所以不妨设：

$$\Phi(B) = \prod_{i=1}^p{(1 - \lambda_i B)} , |\lambda_i| < 1 ; i = 1,2,\cdots,p$$ 则有 $\varphi(B) = \Phi(B) \nabla^d = \left[ \prod_{i=1}^p{(1 - \lambda_i B)} \right] (1 - B)^d$
由上式很容易判断，$ARIMA(p,d,q)$ 模型的广义自回归系数多项式共有 $p + d$ 个根.

其中 $p$ 个根 $\frac{1}{\lambda_1},\cdots,\frac{1}{\lambda_p}$在单位圆外，$d$ 个根在单位圆上.

自回归系数多项式的根即为特征根的倒数，所以 $ARIMA(p,d,q)$ 模型共有 $p + d$ 个根，其中 $p$ 个根在单位圆外，$d$ 个根在单位圆上.

因为有 $d$ 个特征根在单位圆上而非单位圆内，所以当 $d \neq 0$时，$ARIMA(p,d,q)$ 模型不平稳.

---

方差齐性

对于 $ARIMA(p,d,q)$模型，当 $d \neq 0$ 时，不仅均值非齐性，序列方差也非齐性.

以最简单的随机游走模型 $ARIMA(0,1,0)$ 为例：

$$x_t = x_{t-1} + \epsilon_t \\ = x_{t-2} + \epsilon_t + \epsilon_{t-1} \\ \vdots \\ = x_0 + \epsilon_t + \epsilon_{t-1} + \cdots + \epsilon_1$$ 则$Var(x_t) = Var(x_0 + \epsilon_t + \cdots + \epsilon_1) = t \sigma_{\epsilon}^2$

这是一个时间 $t$ 的递增函数，随着时间趋于无穷，序列 $\{x_t\}$ 的方差也趋向于无穷.

但 $1$ 阶差分之后

$$\nabla x_t = \epsilon_t$$ 差分后序列方差齐性 $$Var(\nabla x_t) = \sigma_{\epsilon}^2$$

---

$ARIMA$ 模型建模

在掌握了 $ARMA$ 模型的建模方法后，尝试使用 $ARIMA$ 模型对观察序列建模时一件比较简单的事情了.一般建模流程如下:

---

下面我们以一个具体的实例来演示建模过程:

#数据的准备
> d <- read.table("data/file17.csv",",",header = T)
> x <- ts(d$index,start = 1952)
> plot(x)
>

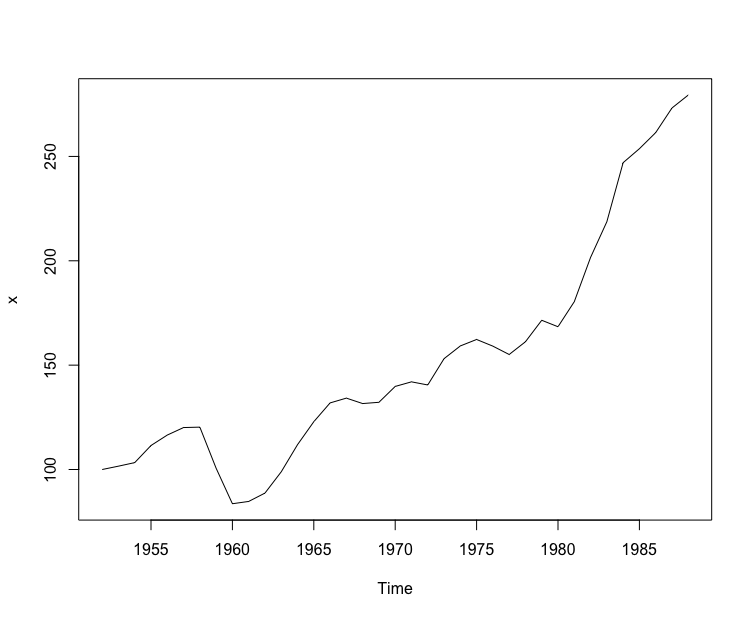
这里是对 1952 ~ 1988 年中国农业实际国民收入指数序列建模.

#一阶差分
> x.dif <- diff(x)
> plot(x.dif)
>

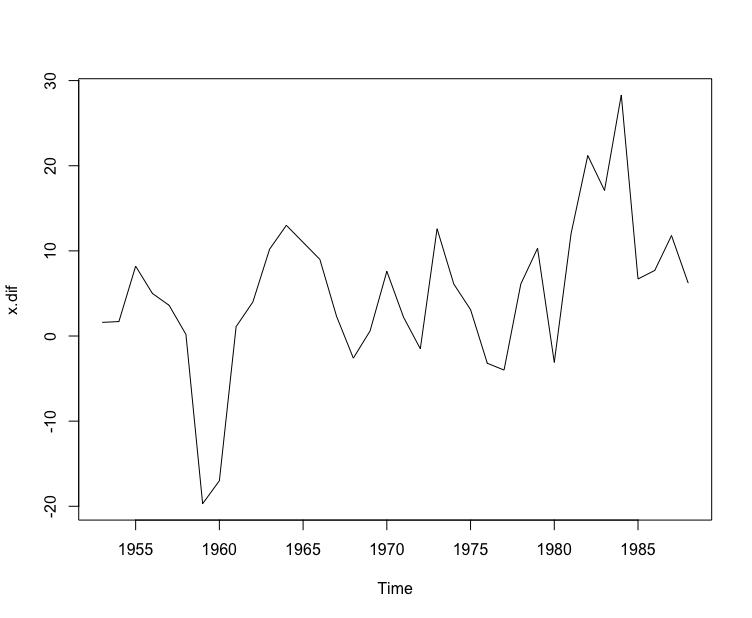
一阶差分后可以看到时序图基本平稳，不用进行二阶差分.

#考察自相关图
> acf(x.dif)
>

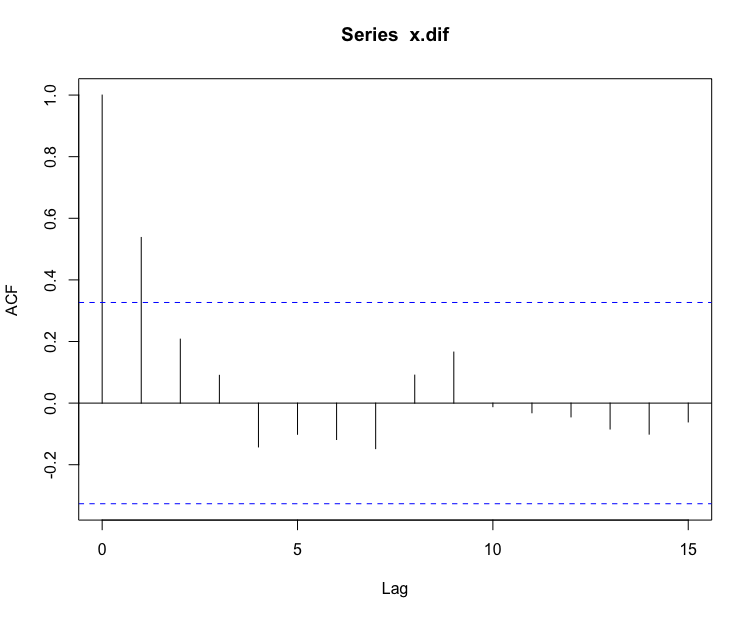
从自相关图中可以看出，一阶滞后后的自相关阶数均在 2 倍标准差范围之内，显示出很强的短期相关性，所以可以认为 1 阶差分后序列平稳，相关系数 1 阶截尾.

#考察偏自相关图
> pacf(x.dif)
>

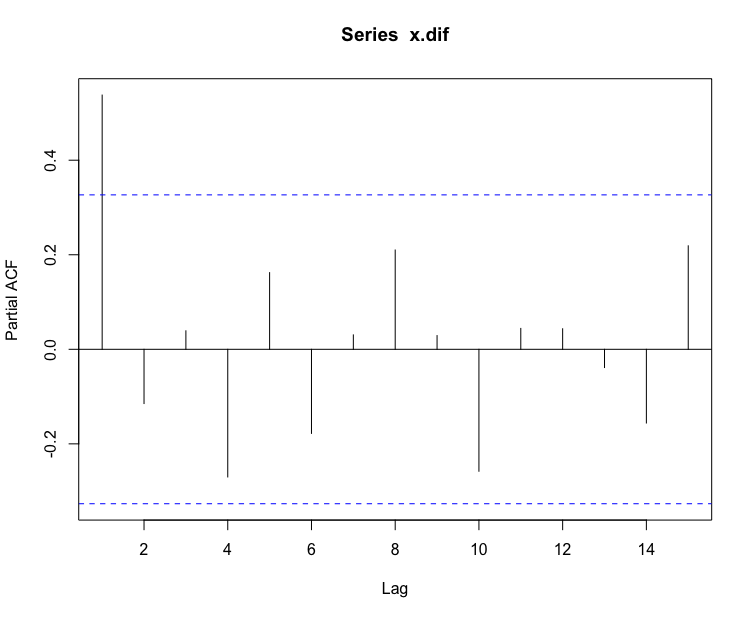
从偏自相关图中看出，0 阶滞后后，偏相关阶数均在 2 倍标准差范围之内，偏自相关系数 0 阶截尾.

综合acf和pacf，确定模型为 $arima(0,1,1)$.

# arima(0,1,1) 模型拟合
> x.fit <- arima(x,order = c(0,1,1))
> x.fit
Call:
arima(x = x, order = c(0, 1, 1))
Coefficients:
         ma1
      0.7355
s.e.  0.1545
sigma^2 estimated as 61.95:  log likelihood = -125.74,  aic = 255.49
>

从Coefficients参数值可以得到拟合模型的表达式为

$$x_t = x_{t-1} + \epsilon_t + 0.7355 \epsilon_{t-1} ,\epsilon_t \approx N(0,61.95)$$

#残差白噪声检测，考察拟合效果
> for(i in 1:2) print(Box.test(x.fit$residuals,lag = 6*i))
    Box-Pierce test
data:  x.fit$residuals
X-squared = 3.3169, df = 6, p-value = 0.7681
    Box-Pierce test
data:  x.fit$residuals
X-squared = 6.0284, df = 12, p-value = 0.9146
>

对模型拟合后的残差做白噪声检测，从p-value = 0.9146可以看出，残差是白噪声非常显著，说明 arima(0,1,1)模型拟合的很好.

---

$ARIMA$ 模型预测

模型建立好之后，我们就可以用来预测了.在最小均方误差预测原理下，$ARIMA$模型和 $ARMA$模型的预测方法非常相似.

$ARIMA(p,d,q)$ 模型的一般表示方法为:

$$\Phi(B)(1 - B)^d x_t = \Theta(B) \epsilon_t$$
和 $ARMA$模型一样，也可以用随机扰动项的线性函数表示: $$x_t = \epsilon_t + \Psi_1 \epsilon_{t-1} + \Psi_2 \epsilon_{t-2} + \cdots \\ = \Psi(B) \epsilon_t$$
式中，$\Psi_1,\Psi_2,\cdots$ 的值由如下等式确定: $$\Phi(B) (1 - B)^d \Psi(B) = \Theta(B)$$ 如果把 $\Phi^*(B)$ 记为广义自相关函数，有 $$\Phi^*(B) = \Phi(B)(1 - B)^d = 1 - \widetilde{\phi}_1 B - \widetilde{\phi}_2 B^2 - \cdots$$
容易验证，$\Psi_1,\Psi_2,\cdots$ 的值满足如下递推公式: $$\begin{cases} \Psi_1 = \widetilde{\phi}_1 - \theta_1 \\ \Psi_2 = \widetilde{\phi}_2 \Psi_1 + \widetilde{\phi}_1 - \theta_2 \\ \vdots \\ \Psi_j = \widetilde{\phi}_1 \Psi_{j-1} + \cdots + \widetilde{\phi}_{p+d} \Psi_{j-p-d} - \theta_j \end{cases}$$
式中，$\Psi_j = \begin{cases} 0, j < 0 \\ 1, j = 0 \end{cases};\theta_j = 0 (j > d)$

那么，$x_{t+l}$的真实值为:

$$x_{t+l} = (\epsilon_{t+l} + \Psi_1 \epsilon_{t+l-1} + \cdots + \Psi_{l-1} \epsilon_{t+1}) + (\Psi_l \epsilon_t + \Psi_{l+1} \epsilon_{t-1} + \cdots )$$

由于 $\epsilon_{t+l},\epsilon_{t+l-1},\cdots,\epsilon_{t+1}$ 的不可获得性，所以 $x_{t+l}$ 的估计值只能为:

$$\hat{x}_t(l) = \Psi^*_0 \epsilon_t + \Psi^*_1 \epsilon_{t-1} + \Psi^*_2 \epsilon_{t-2} + \cdots$$
真实值与预测值之间的均方误差为: $$E[x_{t+l} - \hat{x}_t(l)]^2 = (1 + \Psi_1^2 + \cdots + \Psi_{l-1}^2)\sigma_{\epsilon}^2 + \sum_{j=0}^{\infty}{(\Psi_{l+j} - \Psi_j^*)^2 \sigma_{\epsilon}^2}$$
要使均方误差最小，当且仅当 $$\Psi_j^* = \Psi_{l+j}$$ 所以在均方误差最小原则下，$l$ 期预测值为: $$\hat{x}_t(l) = \Psi_l \epsilon_t + \Psi_{l+1} \epsilon_{t-1} + \Psi_{l+2} \epsilon_{t-2} + \cdots$$
$l$ 期预测误差为: $$e_t(l) = \epsilon_{t+l} + \Psi_1 \epsilon_{t+l-1} + \cdots + \Psi_{l-1} \epsilon_{t+1}$$
真实值等于预测值加上预测误差: $$x_{t+l} = (\epsilon_{t+l} + \Psi_1 \epsilon_{t+l-1} + \cdots + \Psi_{l-1} \epsilon_{t+1}) + (\Psi_l \epsilon_t + \Psi_{l+1} \epsilon_{t-1} + \cdots ) \\ = e_t(l) + \hat{x}_t(l)$$
$l$ 期预测误差的方差为: $$Var[e_t(l)] = (1 + \Psi_1^2 + \cdots + \Psi_{l-1}^2 ) \sigma_{\epsilon}^2$$

---

下面依然是以中共农业实际国民收入指数序列作为期 10 年的预测来演示:

#引入必要的时间序列预测包
> library(zoo)
> library(forecast)
# arima 模型拟合
> d <- read.table("data/file17.csv",",",header = T)
> x <- ts(d$index, start = 1952)
> x.fit <- arima(x,order = c(0,1,1))
# 模型预测
> x.fore <- forecast(x.fit,h = 10)
> x.fore
     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
1989       283.0082 272.9213 293.0950 267.5816 298.4347
1990       283.0082 262.8045 303.2118 252.1094 313.9070
1991       283.0082 256.2756 309.7407 242.1243 323.8921
1992       283.0082 251.0540 314.9624 234.1384 331.8779
1993       283.0082 246.5731 319.4432 227.2856 338.7308
1994       283.0082 242.5860 323.4304 221.1878 344.8286
1995       283.0082 238.9582 327.0581 215.6396 350.3767
1996       283.0082 235.6073 330.4090 210.5149 355.5015
1997       283.0082 232.4782 333.5382 205.7292 360.2871
1998       283.0082 229.5318 336.4845 201.2231 364.7932
# 绘制预测图
> plot(x.fore)
>

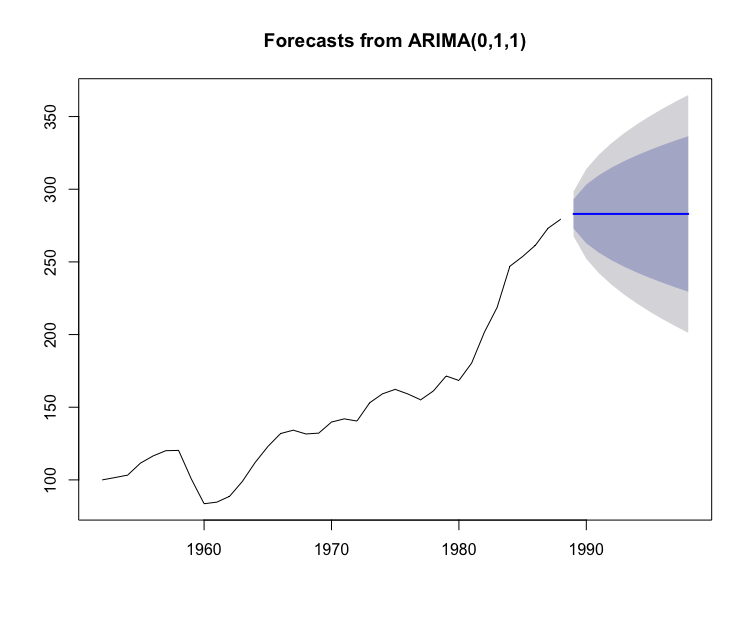
arima()函数用来拟合模型，forecast()函数利用拟合好的模型来进行预测，具体的用法可以使用 help(arima)以及 help(forecast)命令查看帮助文档.

$ARIMA(p,d,q)$模型中，如果有部分系数缺省了，那么该模型称为疏系数模型，记为 $ARIMA((p_1,\cdots,p_m),d,(q_1,\cdots,q_n))$，其中 $p_1,\cdots,p_m$，以及$q_1,\cdots,q_n$分别表示自相系数的非零阶数和移动平滑部分的非零阶数.

在 R 中，arima()函数的transform.pars参数和fixed参数用来调节疏系数模型的参数，详情请help(arima)