机器学习篇

拉格朗日乘子法

拉格朗日乘子法是为了求解最优化问题而设计的一种方法，本篇会详细讲解下拉格朗日乘子法的解法过程，以及由来；进一步讲解拉格朗日乘子法的泛化形式，即KKT条件；

笔者在学校时也只是知道拉格朗日乘子法怎么用，但在学习 SVM 时才首次需要深入理解 拉格朗日乘子法和KKT条件的原理，这里将学到的知识做个总结与分享，希望能从头到尾讲明白.

最优化问题的几种情况

最优化问题大致有三类：无约束最优化问题，有等式约束的最优化问题，有不等式约束的最优化问题。

无约束的最优化问题

数学描述为:

$$\min_{x} f(x)$$ 表示函数 $f(x)$ 为 $x$ 求最小值，并且对变量 $x$ 没有任何约束条件.

这类问题最简单，常用的方法是 Fermat定理，即

$$\frac{d f(x)}{d x} = 0$$
$f(x)$ 对 $x$ 求导，并令导数等于零，可以求得候选最优值，再在这些候选值中验证；如果 $f(x)$ 是凸函数，可以保证是最优解.

若 $x$ 为向量，即 $\boldsymbol{x} = (x_1,x_2,\cdots,x_n)$，则 $f(\boldsymbol{x})$ 需要对每个分量 $x_i$ 求偏导，即可求解.如 $\frac{\partial f(x)}{\partial x_i} = 0,i = 1,2,\cdots,n$

且以下篇幅中的记法 $x,y$ 等等变量都可以是向量（为了方便），若为向量，则求导则换成是对每个分量求偏导.

---

有等式约束的最优化问题

数学形式为:

$$\begin{array} & \min\;f(x)\\s.t.\;h_{i}(x)=0\;\;\;\;i=1,2,\cdots,n \end{array}$$
表示在 $h_i(x) = 0,i = 1,2,\cdots,n$ 的条件下求 $f(x)$ 的最小值.

这类最优化问题可以用拉格朗日乘子法求解，即通过一个拉格朗日系数 $\lambda_i$ 把等式约束和目标函数组合成一个式子，表达式如下:

$$\begin{array} & L(x,\lambda) = f(x) + \sum_{i=1}^n \lambda_i h_i(x) \\ \min_{x} L(x,\lambda) \end{array}$$
其中 $\lambda_{i}\ne{0},i = 1,2,\cdots,n$，称为拉格朗日乘子。

变换后对 $L(x,\lambda)$ 函数求极值就转换为了无约束最优化问题，可以利用上面的 Fermat 定理求解.

---

为了读者能方便理解拉格朗日乘子法的具体操作，下面我们以一个简单的例子来说明:

【例 1】: 求离散分布的最大熵.

离散分布的熵表示为:

$$\begin{array} & f(x_1,x_2,\cdots,x_n) = -\sum_{k=1}^n p_k \log_{2} p_k \\ g(p_1,p_2,\cdots,p_n) = \sum_{k=1}^n p_k = 1 \end{array}$$ 根据拉格朗日乘子法，设 $$F(p_1,p_2,\cdots,p_n) = f(p_1,p_2,\cdots,p_n) + \lambda \left[ g(p_1,p_2,\cdots,p_n) - 1 \right]$$ 对所有的 $p_k$ 求偏导，得: $$\frac{\partial}{\partial p_k} \left( -\sum_{k=1}^n p_k \log_{2} p_k + \lambda \left( \sum_{k=1}^n p_k - 1 \right) \right) = 0$$ 计算出这 $n$ 个等式的微分，得到: $$\begin{array} & \because \left( p_k \log_{2} p_k \right)' = p_k' \log_{2} p_k + p_k \left( \log_{2} p_k \right)' \\ \qquad \qquad = \log_{2} p_k + \frac{1}{\ln 2} \\ \therefore -\left( \frac{1}{\ln 2} + \log_{2} p_k \right) + \lambda = 0 \\ \because \sum_{k=1}^n p_k = 1 \\ \therefore p_k = \frac{1}{n} \end{array}$$ 这说明所有的 $p_k$ 都相等，得到: $p_k = \frac{1}{n}$，因此均匀分布可得到最大熵的值.

这恰好说明了均匀分布时，系统是处于最混乱的状态，则熵最大.

---

有不等式约束的最优化问题

数学描述为:

$$\begin{array} & \min_{x} f(x) \\ s.t. \quad g_i(x) \leq 0,i = 1,2,\cdots,n \\ \qquad \quad h_j(x) = 0,j = 1,2,\cdots,m \end{array}$$

对于这类问题，常用的方法就是 KKT条件(Karush-Kuhn-Tucher)，同样的，我们把所有的等式、不等式约束与 $f(x)$ 写成一个式子，这个式子也叫拉格朗日函数，系数也称为拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件就称为 KKT条件.

具体来说就是求解原问题的对偶问题为:

$$\begin{array} & L(x,a,b) = f(x) + \sum_{i = 1}^n a_i*g_i(x) + \sum_{j=1}^m b_j*h_j(x) \\ \min_{x} L(x,a,b) \end{array}$$ 其中 $a_i \geq 0,b_j \geq 0$.

KKT条件是说最优值必须满足以下条件:

$$\begin{cases} \frac{\partial L(x,a,b)}{\partial x} &=& 0 \\ g_i(x) &\leq& 0 , h_j(x) = 0 \\ a_i*g_i(x) &=& 0 \end{cases}$$ 求取这三个等式之后就能得到候选最优值。

分析这几个条件，发现第一个条件就是 Fetmat定理，第二个条件就是原问题的等式约束，保证最优点必须是一个可行解，第三个条件比较有意思，因为 $g_i(x) \leq 0$，有方向，所以对系数 $a_i$ 也要由方向约束，使得 $a_i * g_i(x) = 0$，保证 $\min_{x} L(x,a,b) = \min_{x} f(x)$，而等式约束是没有方向的，所以对系数 $b_j$ 没有约束；后面我们会详细推导出 KKT条件的由来.

---

导数求解极值的原理

这里以一个通俗的例子来说明下导数求解极值的原理。

假设你在一座山 $M$ 上，你的目标是爬到山顶，也就是说你希望自己的海拔足够高，当你真正到达山腰时，很容易“只缘身在此山中，不识此山真面目”，这时候如何判断是真的在往上爬呢，还是在往下走呢 ？

在肉眼所能看见的小范围内，你可以通过周边的局部地形来判断，假设它大概是这样的:

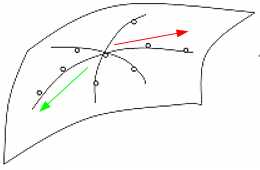
你就知道应该往高处（大概为红色箭头的方向）走，而不是往绿色箭头方向。

当然不一定一直沿着这个方向直线式上升，可能还需要走到某个地方，再次做一下这种局部的考察，调整一下方向，保证自己能向高处走.

有个疑问就是，什么是“高”的一边，如何来判定呢？

我们知道，海拔 $f(x,y,z) = z$，我们希望能够找到山面上的海拔最高点（山顶），即 梯度 $\nabla f = (0,0,1)$，垂直于地平线，其中 $\nabla$ 表示对函数 $f$ 求梯度.

关于梯度有个很自然的结论是: 沿梯度的方向是 $f$ 增长最快的方向，反方向就是下降最快的方向.

所以直观上沿着与梯度方向成锐角的方向移动，那么 $f$ 的值应该会增加.

而在山面上，我们可以通过天空来确定梯度方向（$\nabla f = (0,0,1)$ 当然指向高高的天空啦）与垂直向上方向成锐角的方向的地形，也就是“高”的一边.

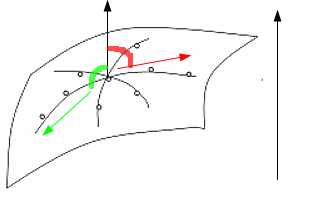
可以看见，红色的角是锐角，所以沿此方向海拔上升，绿色的角是钝角，所以沿此方向海拔下降.

所有我们可以移动的方向，叫做这一点的切空间。

那么，什么时候才能知道我们到达了山顶呢？

我们可以想象，随着往山顶越来越接近，移动方向应该会与山顶的梯度方向的夹角越来越大，逐渐接近垂直。

假设 $P$ 点为山顶，那么在这点上，切空间上任何一个方向与山顶梯度方向的夹角都不可能是锐角，否则我们就可以沿锐角的方向继续升高了。

所以山顶处切空间只能够与梯度方向垂直，用数学语言描述就是

$$\nabla f = 0$$

这也就是 Fetmat定理的含义.

读者可参看知乎上面的回答 : https://www.zhihu.com/question/38586401

---

拉格朗日乘子法的原理

这里就有个疑问，为什么将约束条件乘以系数后与原函数合并成一个式子后就能求得最优值了？

我们设想目标函数 $z = f(x)$，$x$ 是向量，$z$ 取不同的值，相当于可以投影在 $x$ 构成的平面（曲面）上，即成为等高线。如下图所示:

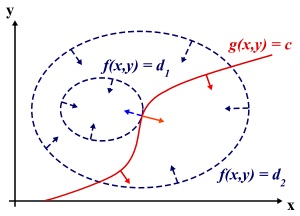
图中目标函数是 $f(x,y)$，这里 $x$ 是标量，虚线是等高线，现在假设我们的约束为 $g(x,y) = c$，$x$ 是向量，在 $x$ 构成的平面或者曲面上是一条曲线；

假设 $g(x,y)$ 与等高线 $f(x,y) = d_2$ 相交，交点就是同时满足等式约束和目标函数的可行域的值，但此时肯定不是最优值，因为相交意味着肯定还存在其它的等高线在该等高线的内侧或外侧，使得新的等高线与目标函数的交点的值更大或更小，只有等高线与目标函数相切时，才可能取得最优值。

相切意味着等高线和目标函数的曲线在切点的法向量必须共线，所以最优值必须满足: $\nabla f = \lambda \nabla g$，其中，$\lambda$ 是常数且不为零。这个等式就是 $L(x,\lambda)$ 对 $x$ 求导的结果.

---

我们还是以一个简单的例子来说明.

【例 2】: 求双曲线 $xy = 3$ 上离原点最近的点.

首先我们根据问题提取出对应的数学模型，即:

$$\begin{array} & f(x,y) = x^2 + y^2 \\ \min f(x,y) \\ s.t. \quad xy = 3 \end{array}$$ 可以看出这是一个典型的有等式约束的最优化问题；我们将 $x^2 + y^2 = c$ 的曲线族画出来，如下图所示:

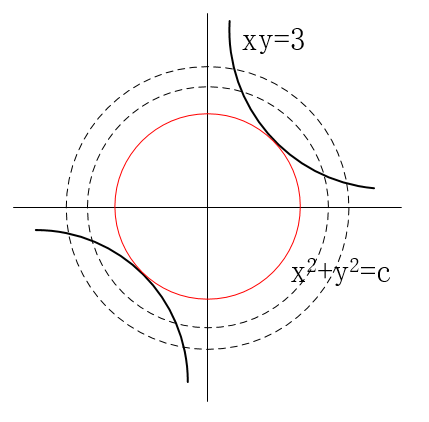
当曲线族中的圆与 $xy = 3$ 曲线相切时，切点到原点的距离最短。也就是说，当 $f(x,y) = c$ 的等高线与双曲线 $g(x,y) = xy - 3$ 相切时，我们可以得到上述最优化问题的一个极值.

我们知道，如果两个曲线相切，在切点处，它们的切线相同，法向量是共线的，即 $\nabla f = \lambda \nabla g$，其中 $\nabla$ 表示对函数求导（求法向量）.

这时，我们就将原有的约束优化问题转化为了一种对偶的无约束优化问题，如下:

原问题:

$$\begin{array} & \min f(x,y) \\ s.t. \quad xy = 3 \end{array}$$
对偶问题由 $\nabla f = \lambda \nabla g$ 得: $$\begin{array} & \frac{\partial f(x,y)}{\partial x} = \lambda * \frac{\partial g(x,y)}{\partial x} \\ \frac{\partial f(x,y)}{\partial y} = \lambda * \frac{\partial g(x,y)}{\partial y} \\ xy = 3 \end{array}$$ 通过求解对偶问题的方程组，就可以获得原问题的解，即: $$\begin{array} & 2x = \lambda * y \\ 2y = \lambda * x \\ xy = 3 \end{array}$$ 通过求解得最优解为 $(x,y) = (\sqrt{3},\sqrt{3})$ 或者是 $(x,y) = (-\sqrt{3},-\sqrt{3})$

---

KKT条件的原理

在实际问题中，我们往往面临的是不等式约束，比如不超过多少时间，不超过多少人力，不超过多少成本等等，所以科学家们拓展了拉格朗日乘数法，增加了KKT条件之后便可以用拉格朗日乘数法来求解不等式约束的优化问题了。

下面就直接来推导KKT条件产生的过程，以一个简单的只有不等式约束的最优化问题来说明:

原问题为:

$$\begin{array} & \min_{x} f(x) \\ s.t. \quad g_k(x) \leq 0,k = 1,2,\cdots,n \end{array}$$ 我们定义函数 $L(x,u)$ 为 $$L(x,\boldsymbol{u}) = f(x) + \sum_{k=1}^n u_k g_k(x)$$ 其中，$u_k \geq 0,g_k(x) \leq 0$

$$\begin{array} & \because u_k \geq 0,g_k(x) \leq 0 \\ \therefore u_g(x) = \sum_{k=1}^n u_k g_k(x) \leq 0 \\ \therefore \max_{u} L(x,u) = \max_{u} \left( f(x) + u_g(x) \right) \\ \qquad \qquad \qquad = \max_{u} f(x) + \max_{u} u_g(x) \\ \qquad \qquad \qquad = f(x) + 0 = f(x) \qquad \eqref{1}\\ \therefore \min_{x} f(x) = \min_{x} \max_{u} L(x,u) \end{array}$$

下面我们再来探讨另一边，即 $\max_{u} \min_{x} L(x,u)$ :

$$\begin{array} & \max_{u} \min_{x} L(x,u) &=& \max_{u} \left[ \min_{x} f(x) + \min_{x} u_g(x) \right] \\ &=& \max_{u} \min_{x} f(x) + \max_{u} \min_{x} u_g(x) \\ &=& \min_{x} f(x) + \max_{u} \min_{x} u_g(x) \end{array}$$
下面单独考虑 $\max_{u} \min_{x} u_g(x)$ :

$$\begin{array} & \because u_k \geq 0,g_k(x) \leq 0 \\ \therefore \min_{x} u_g(x) = \begin{cases} 0, & if \ u = 0 \ or \ g(x) = 0;\\ -\infty, & if \ u>0 \ and \ g(x) < 0; \end{cases} \\ \therefore \max_{u} \min_{x} u_g(x) = 0,\\ \qquad s.t. \ u = 0 \ or \ g(x) = 0 \\ \therefore \max_{u} \min_{x} L(x,u) = \min_{x} f(x) + \max_{u} \min_{x} u_g(x) \\ \qquad \qquad \qquad \qquad = \min_{x} f(x) \qquad \eqref{2} \\ \qquad s.t. \ u = 0 \ or \ g(x) = 0 \end{array}$$

于是我们可得到当 $u = 0 \ or \ g(x) = 0$ 时，有

$$\min_{x} \max_{u} L(x,u) = \min_{x} f(x) = \max_{u} \min_{x} L(x,u)$$

亦即

$$\left.\begin{matrix}L(x,\mu)=f(x)+\sum_{k=1}^q\mu_{k}g_{k}(x)\\\mu_{k}\ge{0}\\g_{k}(x)\le{0}\end{matrix}\right\} =>\\ \begin{array} & \min_{x}\max_{\mu}L(x,\mu)=\max_{\mu}\min_{x}L(x,\mu) =\min_{x}f(x) \end{array}$$

我们把 $\max_{\mu}\min_{x}L(x,\mu)$ 称为原问题 $\min_{x}\max_{\mu}L(x,\mu)$ 的对偶问题，

上式表明当满足一定条件时原问题、对偶的解、以及 $\min_{x}f(x)$ 是相同的，且在最优解 $x^*$ 处 $\mu=0\;or\;g(x^*)=0$。把 $x^*$ 代入 $\eqref{1}$ 得 $\max_{\mu}L(x^*,\mu)=f(x^*)$，由 $\eqref{2}$ 得 $\max_{\mu}\min_{x}L(x,\mu) = \min_{x} f(x^*) =f(x^*)$，所以 $L(x^*,\mu)=\min_{x}L(x,\mu)$，这说明 $x^*$ 也是 $L(x,\mu)$ 的极值点，即 $\frac{\partial{L(x,\mu)}}{\partial{x}}|_{x=x^*}=0$。

---

最后总结一下：

$$\left.\begin{matrix} L(x,\mu) &=& f(x) + \sum_{k=1}^q \mu_{k} g_{k}(x) \\ \mu_{k} &\geq& 0 \\ g_{k}(x) &\leq& 0 \end{matrix} \right\} => \\ \begin{cases} \min_{x} \max_{\mu} L(x,\mu) &=& \max_{\mu} \min_{x} L(x,\mu) &=& \min_{x} f(x) &=& f(x^*) \\\\ \mu_{k} g_k(x^*) &=& 0 \\\\ \frac{\partial{L(x,\mu)}}{\partial{x}}|_{x=x^*} &=& 0 \end{cases}$$

KKT条件是拉格朗日乘子法的泛化，如果我们把等式约束和不等式约束一并纳入进来则表现为：

$$\left.\begin{matrix} L(x,\lambda,\mu) &=& f(x) + \sum_{i=1}^{n} \lambda_{i} h_{i}(x) + \sum_{k=1}^q \mu_{k} g_{k}(x) \\ \lambda_{i} &\neq& 0 \\ h_{i}(x) &=& 0 \\ \mu_{k} &\geq& 0 \\ g_{k}(x) &\leq& 0 \end{matrix}\right\} => \\ \left\{ \begin{matrix} \min_{x} \max_{\mu} L(x,\lambda,\mu) &=& \max_{\mu} \min_{x} L(x,\lambda,\mu) = \min_{x} f(x) = f(x^*) \\ \mu_{k} g_{k}(x^*) &=& 0 \\ \frac{\partial{L(x,\lambda,\mu)}}{\partial{x}}|_{x=x^*} &=& 0 \end{matrix}\right.$$

注：$x,\lambda,\mu$都是向量。

$\frac{\partial{L(x,\lambda,\mu)}}{\partial{x}}|_{x=x^*}=0$表明$f(x)$在极值点$x^*$处的梯度是各个$h_{i}(x^*)$和$g_{k}(x^*)$梯度的线性组合。

---

小结

到这里整个拉格朗日乘子法求解最优化问题就讲完了，希望对读者有帮助.