@evilking 2018-04-30T16:11:05.000000Z 字数 4434 阅读 3056

NLP

TrustRank算法

TrustRank是近年来比较受关注的基于链接关系的排名算法。TrustRank 可以翻译为“信任指数”。

TrustRank是改进的PageRank算法，由于PageRank算法只考虑结点的入链和出链，因此使用PageRank进行排序的结果容易被恶意操纵，比如一些垃圾网页链接到很多高质量的网站等手段；而TrustRank算法能有效的解决这个问题，能将来自 Spam 的链接与优质内容带来的真正意义上的好评区分开来.

算法假设

TrustRank算法基于一个基本假设：好的网站很少会链接到坏的网站。反之则不成立，也就是说，坏的网站很少链接到好网站这句话并不成立。正相反，很多垃圾网站会链接到高权威、高信任指数的网站，意图提高自己的信任指数。

基于这个假设，如果能挑选出可以百分之百信任的网站，这些网站的 TrustRank 评为最高，这些TrustRank最高的网站所链接到的网站信任指数稍微降低，但也会很高。与此类似，第二层被信任的网站链接出去的第三层网站，信任度继续下降。由于种种原因，好的网站也不可避免地会链接到一些垃圾网站，不过离第一层网站点击距离越近，所传递的信任指数越高，离第一级网站点击距离越远，信任指数将依次下降。这样，通过TrustRank算法，就能给所有网站计算出相应的信任指数，离第一层网站越远，成为垃圾网站的可能性就越大。

算法原理

先用人工识别出一部分高质量的页面（即“种子”页面），那么由“种子”页面指向的页面也可能是高质量页面，即其TrustRank也高，与“种子”页面的链接越远，页面的TrustRank越低。

TrustRank采用半自动的方法区分垃圾文件和高质量的文件。依靠专家去评估一系列“种子”页面的TrustRank值。一旦确定了“种子”页面，就容易区分好页面和垃圾页面，通过机器分析链接结构来确定其它页面的TrustRank值。

下面以一个示例来演示TrustRank的过程：

结点图1

假设有如图所示的结点图， $V$ 代表结点编号， $E$ 代表有边相连，比如(1,2)表示结点 1 与结点 2 右边相连.

该图用邻接矩阵表示为 $H$ :

结点图2

结点图3

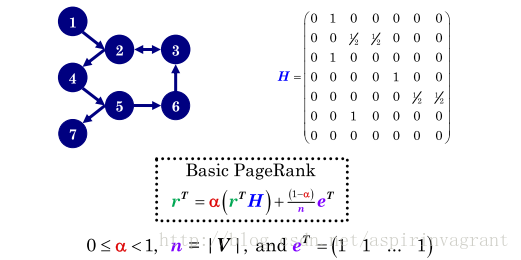
其中， $H(2,3) = \frac{1}{2}$ 表示结点 2 到结点 3 有权值为 $\frac{1}{2}$ 的边相连，值为什么是 $\frac{1}{2}$ 呢，是因为结点 2 有两个出链，则每个出链占比 $\frac{1}{2}$ 。

图中给出了普通 PageRank 的迭代公式：

$\boldsymbol{r}^T = \alpha (\boldsymbol{r}^T H) + \frac{1 - \alpha}{n} \boldsymbol{e}^T$ 其中，

$0 \leq \alpha \leq 1, n = |V|,and \boldsymbol{e}^T = (1,1,\cdots,1)$ ，

$\boldsymbol{r}$ 代表 rank值（即一个结点重要度的向量）.

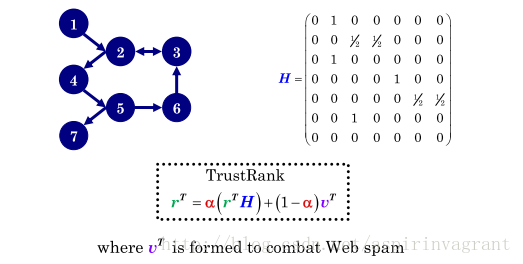
以及 TrustRank的迭代公式：

$\boldsymbol{r}^T = \alpha (\boldsymbol{r}^T H) + (1 - \alpha) \boldsymbol{v}^T$ 其中，

$\boldsymbol{v}^T$ 代表“种子页面”的权值.

选取种子集

TrustRank算法首先要选取一部分可信的页面作为种子集，然后由种子集的 rank值依次迭代计算出其他结点的 rank值。种子页面的选取可以人工选取，或者可以通过相关算法来自动选取.

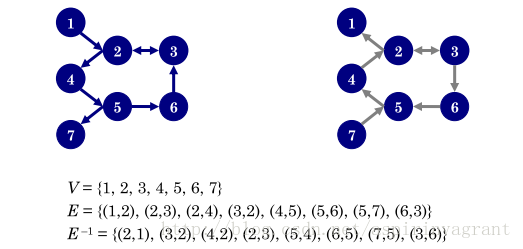
图中显示了有向图的边链接情况，以及该有向图的逆向图的链接情况。

自动筛选候选种子

由此逆向有向图可生成下面的邻接矩阵 :

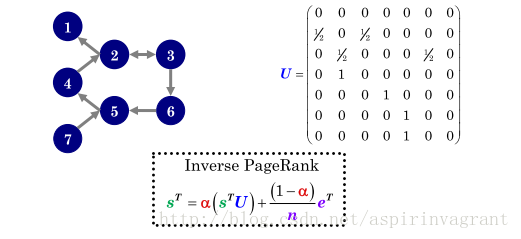
逆向有向图按 PageRank算法逐步迭代，直至稳定：

$\boldsymbol{s}^T = \alpha (\boldsymbol{s}^T U) + \frac{(1 - \alpha)}{n} \boldsymbol{e}^T$ 其中，

$\boldsymbol{s}$ 向量表示可信度值，初始值可设为

$\frac{1}{n}$ 或者为

$\boldsymbol{e}$ ，

$\alpha$ 为学习率，人为指定.

我们从 PageRank的平稳性证明中可知，此处迭代一定会收敛，收敛后的 $\boldsymbol{s}$ 即结点信任度向量，我们将其排序后取前 $t$ 个作为候选种子。

例如此例中，我们初始 $\boldsymbol{s}_0^T$ 设置为 $\boldsymbol{e}^T$ ，最大迭代 $M$ 次，迭代完成后的 $\boldsymbol{s}_{20}^T$ 即为信任度向量，将其排序后我们取前 3 个，得到候选种子集合为 $\boldsymbol{S} = \{ 2,4,5 \}$

人工筛选种子

上步是通过程序自动筛选出一批候选种子页面，为了确保这些候选种子页面是真的完全可信的，需要人工进一步筛选.

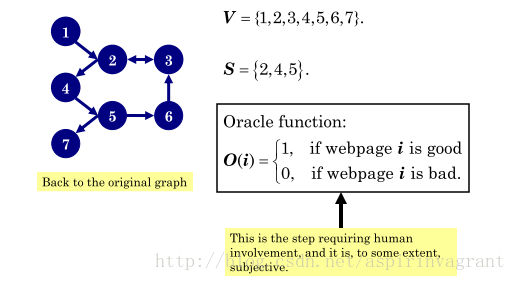
上图显示了从候选种子集合 $\boldsymbol{S} = \{ 2,4,5 \}$ 中人工去确认对应页面是否是 good，如果是则保留，如果不是则舍弃.

假设人工确认的结果如下图:

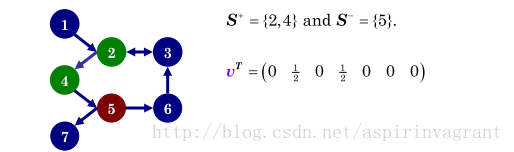
人工确认发现结点 5 不是一个可信的页面，则舍弃掉，那么得到的种子页面集合为 $\boldsymbol{S}^+ = \{ 2,4 \}$ ，由这两个结点初始化权值，即为 $\boldsymbol{v}^T = (0,\frac{1}{2},0,\frac{1}{2},0,0,0)$

创建可信度向量

得到种子页面，获得初始可信度向量后，我们可以基于 TrustRank算法来生成最后的可信度向量.

从例子中可知，首先利用种子页面得到的初始可信度向量设置 TrustRank迭代的初始向量： $\boldsymbol{r}_0^T = \boldsymbol{v}^T$ ，然后根据 TrustRank算法的迭代公式进行迭代，收敛后的 $\boldsymbol{r}_k^T$ 即为最后的 trust值向量.

此图是这个例子的结果图，图说显示 "Basic PageRank"的效果优于 "TrustRank"，可能是人工筛选种子页面的时候有点不同.

但是在一般情况下，TrustRank算法是优于 Basic PageRank算法的.

TrustRank java版本源码分析

TrustRank的逻辑还算比较简单，这里是笔者按上面例子的过程写的TrutRank算法程序.

下载地址为 : https://github.com/evilKing/TrustRankDemo

直接运行 TrustRank类，得到下面的输出：

===========逆向PageRank结果如下：
0.08  0.14  0.08  0.10  0.09  0.06  0.02  
===========选择 3 个候选种子如下：
1, 0.14  
3, 0.10  
4, 0.09  
===========人工确认后假设选取前 2 个种子如下：
0.00  0.50  0.00  0.50  0.00  0.00  0.00  
===========TrustRank 结果如下：
0.00  0.18  0.13  0.15  0.13  0.05  0.05  
===========选择 3 个候选种子如下：
1, 0.18  
3, 0.15  
4, 0.13

可以看到上面输出的结果基本与图中展示的一致.

首先看 main() 方法里：

    public static void main(String[] args) {
        init(); //有向图逻辑结构转换为邻接矩阵
        double[] seedsTmp = selectSeed(20);//逆向 PageRank
        System.out.println("===========逆向PageRank结果如下：");
        for(int i = 0;i < seedsTmp.length; i++){
            System.out.printf("%3.2f  ",seedsTmp[i]);
        }
        System.out.println("\n===========选择 3 个候选种子如下：");
        int[] index = sort(seedsTmp);   //排序，筛选候选种子
        int k = 3;
        for(int i = 0;i < index.length && i < k; i++){
            System.out.printf("%d, %3.2f  \n",index[i],seedsTmp[i]);
        }
        System.out.println("===========人工确认后假设选取前 2 个种子如下：");
        k = 2;  //这里要做人工选择，挑选出完全可信的页面
        double[] v = new double[n];
        for(int i=0;i < 2;i++){
            v[index[i]] = 1.0/k;    //种子页面权重平均
        }
        for(int i = 0;i < v.length; i++){
            System.out.printf("%3.2f  ",v[i]);
        }
        System.out.println("\n===========TrustRank 结果如下：");
        double[] r = trustRank(v, 20);
        for(int i = 0;i < r.length; i++){
            System.out.printf("%3.2f  ",r[i]);
        }
        System.out.println("\n===========选择 3 个候选种子如下：");
        index = sort(r);
        k = 3;
        for(int i = 0;i < index.length && i < k; i++){
            System.out.printf("%d, %3.2f  \n",index[i],r[i]);
        }
    }

其中，候选种子页面的选择迭代过程如下：

    private static double[] selectSeed(int M){
        double[] s_k = e;
        double[] s_k_1 = null;
        int k = 0;
        while (k < M) { //最大迭代 M 次
            // PageRank 迭代公式
            s_k_1 = multiMatrix(s_k, U);
            for(int i = 0;i < s_k_1.length; i++ ){
                s_k_1[i] = s_k_1[i]*alpha + (1-alpha)/n;
            }
            //如果两次迭代误差很小，则认为已收敛
            if(iteratorError(s_k, s_k_1) < iterError){
                break;
            }           
            s_k = s_k_1;
        }
        return s_k;
    }

TrustRank 迭代过程如下：

    private static double[] trustRank(double[] v,int M){
        double[] r_k = v;
        double[] r_k_1 = null;
        int k = 0;
        while (k < M) {
            //与 PageRank不同的是 TrustRank的迭代公式
            r_k_1 = multiMatrix(r_k, H);
            for(int i = 0;i < r_k_1.length; i++ ){
                r_k_1[i] = r_k_1[i]*alpha + (1-alpha)*v[i];
            }
            if(iteratorError(r_k, r_k_1) < iterError){
                break;
            }           
            r_k = r_k_1;
        }
        return r_k;
    }

迭代收敛后的 r 数组，就是页面可信指数，对该可信指数进行排序，就可得到页面排名了.

小结

参考博文：http://blog.csdn.net/aspirinvagrant/article/details/40924539