机器学习篇

CRF 模型

条件随机场（conditional random field,CRF）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔科夫随机场.

条件随机场可以用于不同的预测问题，因本系列教程后面重点在文本挖掘、NLP的标注问题上，为了简化所以主要讲述线性链（linear chain）条件随机场。

概率无向图模型

因 CRF 模型是一种概率无向图模型，为了完整性，我们先简要介绍下什么是概率无向图模型.

模型定义

图（graph）是由结点（node）及连接结点的边（edge）组成的集合.结点和边分别记作 $v$ 和 $e$，结点和边的集合分别记作 $V$ 和 $E$，图记作 $G = (V,E)$.无向图是指边没有方向的图.

概率图模型（probabilistic graphical model）是由图表示的概率分布.设有联合概率分布 $P(Y)$，$Y \in \cal(y)$ 是一组随机变量. 由无向图 $G = (V,E)$ 表示概率分布 $P(Y)$，即在图 $G$ 中，结点 $v \in V$ 表示一个随机变量 $Y_v,Y = (Y_v)_{v \in V}$；边 $e \in E$ 表示随机变量之间的概率依赖关系.

---

局部马尔科夫性：设 $v \in V$ 是无向图 $G$ 中任意一个结点，$W$ 是与 $v$ 有边连接的所有结点，$O$ 是 $v$，$W$ 以外的其他所有结点. $v$ 表示的随机变量是 $Y_v$，$W$ 表示的随机变量组是 $Y_W$，$O$ 表示的随机变量组是 $Y_O$. 局部马尔科夫性是指在给定随机变量组 $Y_W$ 的条件下随机变量 $Y$_v$与随机变量组$Y_O$是独立的，即$$P(Y_v,Y_O|Y_W) = P(Y_v | Y_W)P(Y_O|Y_W)$$在$P(Y_O |Y_W) > 0$时，等价地，$$P(Y_v|Y_W) = P(Y_v|Y_W,Y_O)$$

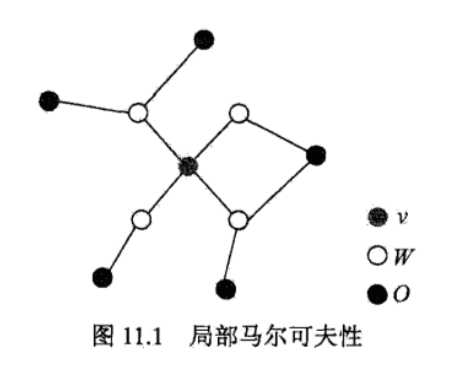
这里只给出局部马尔科夫性，还有等价的成对马尔科夫性、全局马尔科夫性，有兴趣的读者可以参考《统计学习方法》的 CRF 一章.

---

概率无向图模型: 设有联合概率分布 $P(Y)$，由无向图 $G = (V,E)$ 表示，在图 $G$ 中，结点表示随机变量，边表示随机变量之间的依赖关系.如果联合概率分布 $P(Y)$ 满足成对、局部或全局马尔科夫性，就称此联合概率分布为概率无向图模型（probability undirected graphical model），或者马尔科夫随机场（Markov random field）.

概率无向图模型的因子分解

团与最大团: 无向图 $G$ 中任何两个结点均有边连接的结点子集称为团（clique）.若 C 是无向图 $G$ 的一个团，并且不能再加进任何一个 $G$ 的结点使其成为一个更大的团，则称此 $C$ 为最大团（maximal clique）.

---

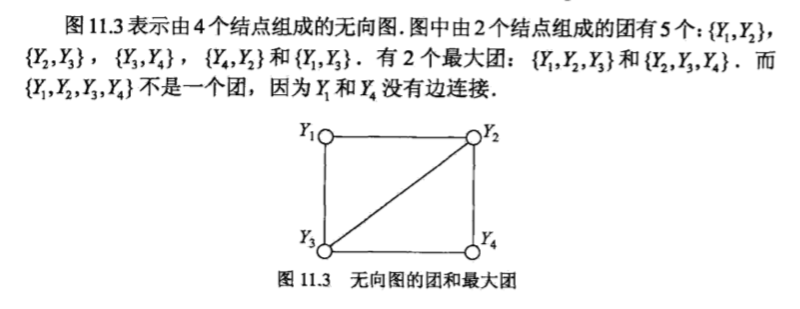
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作，称为概率无向图模型的因子分解（factorization）.

给定概率无向图模型，设其无向图为 $G$，$C$ 为 $G$ 上的最大团，$Y_C$ 表示 $C$ 对应的随机变量.那么概率无向图模型的联合概率分布 $P(Y)$ 可写作图中所有最大团 $C$ 上的函数 $\Psi_C(Y_C)$ 的乘积形式，即

$$P(Y) = \frac{1}{Z} \prod_C \Psi_C(Y_C)$$ 其中，$Z$ 是规范化因子（normalization factor），由式 $$Z = \sum_Y \prod_C \Psi_C(Y_C)$$ 给出.规范化因子保证 $P(Y)$ 构成一个概率分布.函数 $\Psi_C(Y_C)$ 称为势函数（potential function）.这里要求势函数 $\Psi_C(Y_C)$ 是严格正的，通常定义为指数函数: $$\Psi_C(Y_C) = \exp{\{ -E(Y_C) \}}$$

Hammersley-Clifford 定理: 概率无向图模型的联合概率分布 $P(Y)$ 可以表示为如下形式:

$$P(Y) = \frac{1}{Z} \prod_C \Psi_C(Y_C) \\ Z = \sum_Y \prod_C \Psi_C(Y_C)$$

其中，$C$ 是无向图的最大团，$Y_C$ 是 $C$ 的结点对应的随机变量，$\Psi_C(Y_C)$ 是 $C$ 上定义的严格正函数，乘积是将无向图上所有的最大团的势函数相乘.

---

条件随机场

定义

有了上面的概率无向图模型基础，下面我们来定义条件随机场.

条件随机场: 设 $X$ 与 $Y$ 是随机变量，$P(Y|X)$ 是在给定 $X$ 的条件下 $Y$ 的条件概率分布. 若随机变量 $Y$ 构成一个由无向图 $G = (V,E)$ 表示的马尔科夫随机场，即

$$P(Y_v|X,Y_w,w \neq v) = P(Y_v|X,Y_w,w \approx v)$$ 对任意结点 $v$ 成立，则称条件概率分布 $P(Y|X)$ 为条件随机场.式中 $w \approx v$ 表示在图 $G = (V,E)$ 中与结点 $v$ 有边连接的所有结点 $w$，$w \neq v$ 表示结点 $v$ 以外的所有结点，$Y_v,Y_u$ 与 $Y_w$ 为结点 $v,u$ 与 $w$ 对应的随机变量.

在该定义中并没有要求 $X$ 和 $Y$ 具有相同的结构. 现实中，一般假设 $X$ 和 $Y$ 有相同的图结构.

在很多自然语言处理的标注问题中，都是应用的线性链条件随机场，$X,Y$ 的结构相同，都是线性链.

线性链条件随机场: 设 $X = (X_1,X_2,\cdots,X_n),Y = (Y_1,Y_2,\cdots,Y_n)$ 均为线性链表示的随机变量序列，若在给定随机变量序列 $X$ 的条件下，随机变量序列 $Y$ 的条件概率分布 $P(Y|X)$ 构成条件随机场，即满足马尔科夫性:

$$P(Y_i | X,Y_1,\cdots,Y_{i-1},Y_{i+1},\cdots,Y_n) = P(Y_i | X,Y_{i-1},Y_{i+1}) \\ i = 1,2,\cdots,n (在 i = 1 和 n 时只考虑单边)$$
则称 $P(Y|X)$ 为线性链条件随机场. 在标注问题中，$X$ 表示输入观测序列，$Y$ 表示对应的输出标记序列或状态序列.

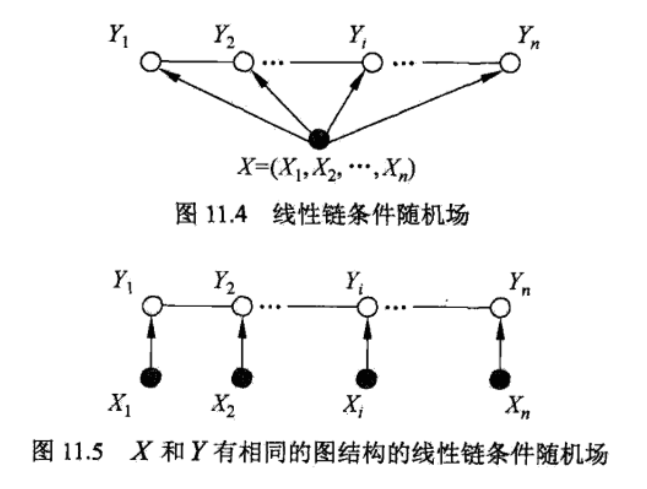
在线性链中，一个结点所在的最大团就两个，与其前一个结点构成一个最大团，与其后一个结点构成第二个最大团，于是线性链条件随机场的概率分布的分解式为:

$$P(Y|X) = \frac{1}{Z} \prod_{i = 1}^N \exp{\{E(Y_i,Y_{i+1})\}}$$

---

线性链条件随机场的参数化形式

设 $P(Y|X)$ 为线性链条件随机场，则在随机变量 $X$ 取值为 $x$ 的条件下，随机变量 $Y$ 取值为 $y$ 的条件概率具有如下形式:

$$P(y|x) = \frac{1}{Z(x)} \exp{\left( \sum_{i,k} \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l(y_i,x,i) \right)}$$ 其中， $$Z(x) = \sum_y \exp{\left( \sum_{i,k} \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l(y_i,x,i) \right)}$$

式中，$t_k,s_l$ 是特征函数，$\lambda_k,\mu_l$ 是对应的权值. $Z(x)$ 是规范化因子，求和是在所有可能的输出序列上进行的.

上两式是线性链条件随机场模型的基本形式，表示给定输入序列 $x$，对输出序列 $y$ 预测的条件概率.

式中 $t_k$ 是定义在边上的特征函数，称为转移特征，因为它依赖于当前位置 $y_i$ 和前一位置 $y_{i-1}$；

$s_l$ 是定义在结点上的特征函数，称为状态特征，它仅依赖于当前位置.

$t_k,s_l$ 都依赖于位置，是局部特征函数.通常，特征函数 $t_k,s_l$ 取值为 1 或 0；当满足特征条件时取值为 1，否则为 0. 条件随机场完全由特征函数 $t_k,s_l$ 和对应的权值 $\lambda_k,\mu_l$ 确定.

---

以一个简单的例子来说明什么是特征函数:

比如有一标注问题：输入观测句子为 $X = (小,明,来,自,武,汉)$，输出标记序列为 $Y = (Y_1,Y_2,Y_3,Y_4,Y_5,Y_6)$，其中 $Y_1,\cdots,Y_6$ 取值于 $y = (PER\_B,PER\_E,O,POS\_B,POS\_E)$.

我们要识别出该句子中的人名 “小明” 和地名 “武汉”，于是可以构造特征函数如下:

$$\begin{array} & t_1(y_{i-1},y_i,x,i) &=& \begin{cases} 1, & y_{i-1} = PER\_B,y_i = PER\_E,x,i,(i = 2,3,\cdots,6) \\ 0,& 其他 \end{cases} \\ t_2(y_{i-1},y_i,x,i) &=& \begin{cases} 1, & y_{i-1} = POS\_B,y_i = POS\_E \\ 0,& 其他 \end{cases} \\ \cdots \cdots \end{array}$$

假设我们就定义这两个特征函数（当然你可以定义多个，看你具体的应用场景是什么），这里是为了做命名实体识别，所以上面这两个特征函数都是转移特征函数；另外这里主要是考察特征函数，忽略特征函数的权值系数，则假设权值系数都取 1.

其中 $t_1(y_{i-1},y_i,x,i)$ 表示位置 $i$ 标注为 $PER\_E$，且位置 $i-1$ 标注为 $PER\_B$ 时满足该特征.（这一特征提取的是人名）

$t_2(y_{i-1},y_i,x,i)$ 表示位置 $i$ 标注为 $POS\_E$，且位置 $i-1$ 标注为 $POS\_B$ 时满足该特征.（这一特征提取的是地名）

所以只有当 $Y$ 序列被标注为 $(PER\_B,PER\_E,O,O,POS\_B,POS\_E)$ 时特征函数的期望才是最大的，而此标注序列能正确的提取出人名和地名.

特征函数是 CRF 的核心，同时也不是特别好理解，读者可以通过这篇博客来体会： http://www.jianshu.com/p/55755fc649b1

---

条件随机场的简化形式

条件随机场还可以由简化形式表示，将局部特征转换成全局特征.

注意到条件随机场的条件概率表达式中同一特征在各个位置都有定义，可以对同一特征在各个位置求和，将局部特征函数转换为一个全局特征函数，这样就可以将条件随机场写成权值向量和特征向量的内积形式，即条件随机场的简化形式.

为了简便起见，首先将转移特征和状态特征及其权值用统一的符号表示.设有 $K_1$ 个转移特征，$K_2$ 个状态特征，$K = K_1 + K_2$，记

$$f_k(y_{i-1},y_i,x,i) = \begin{cases} t_k(y_{i_1},y_i,x,i), & k = 1,2,\cdots,K_1 \\ s_l(y_i,x,i), & k = K_1 +l;l = 1,2,\cdots,K_2 \end{cases}$$

然后，对特征与状态特征在各个位置 $i$ 求和，记作

$$f_k(y,x) = \sum_{i=1}^n f_k(y_{i-1},y_i,x,i), k = 1,2,\cdots,K$$

$f_k(y,x)$ 函数是 $f_k$ 特征函数在所有位置上的累积值.

$f_k$ 特征函数上面做了统一，可表示转移特征或者状态特征.

用 $w_k$ 表示特征 $f_k(y,x)$ 的权值，即

$$w_k = \begin{cases} \lambda_k, & k = 1,2,\cdots,K_1 \\ \mu_l, & k = K_1+l;l = 1,2,\cdots,K_2 \end{cases}$$

统一特征函数的权值系数表示.

于是，条件随机场可表示为:

$$P(y|x) = \frac{1}{Z(x)} \exp{\sum_{k=1}^K w_k f_k(y,x)} \\ Z(x) = \sum_y \exp{\sum_{k=1}^K w_k f_k(y,x)}$$

若以 $w$ 表示权值向量，即

$$\boldsymbol{w} = (w_1,w_2,\cdots,w_K)^T$$
以 $\boldsymbol{F}(y,x)$ 表示全局特征向量，即 $$\boldsymbol{F}(y,x) = (f_1(y,x),f_2(y,x),\cdots,f_K(y,x))^T$$

则条件随机场可改写成向量 $\boldsymbol{w}$ 与 $\boldsymbol{F}(y,x)$ 的内积形式:

$$P_{\boldsymbol{w}}(y|x) = \frac{\exp\{\boldsymbol{w} \cdot \boldsymbol{F}(y,x)\}}{Z_{\boldsymbol{w}}(x)}$$

其中，

$$Z_{\boldsymbol{w}}(x) = \sum_y \exp\{\boldsymbol{w} \cdot \boldsymbol{F}(y,x)\}$$

这一步变换都比较简单，主要是认准两个元素————位置 和 特征函数，这两个元素可理解为两维的矩阵，不同的是按横向累加还是纵向累加.

---

条件随机场的矩阵形式

条件随机场还可以由矩阵表示，改写成类似于 HMM 中的转移矩阵.

假设 $P_{\boldsymbol{w}}(y|x)$ 是由上面给出的线性链条件随机场，表示对给定观测序列 $x$，相应的标记序列 $y$ 的条件概率.引进特殊的起点和终点状态标记 $y_0 = start,y_{n+1} = stop$，这时 $P_{\boldsymbol{w}}(y|x)$ 可以通过矩阵形式表示.

对观测序列 $x$ 的每一个位置 $i = 1,2,\cdots,n+1$，定义一个 $m$ 阶矩阵（$m$ 是标记 $y_i$ 取值的个数）

$$M_i(x) = \left[ M_i(y_{i-1},y_i | x) \right] \\ M_i(y_{i-1},y_i | x) = \exp{\left( W_i(y_{i-1},y_i | x) \right)} \\ W_i(y_{i-1},y_i | x) = \sum_{k = 1}^K w_k f_k(y_{i-1},y_i,x,i)$$
这就类似于 HMM 的转移矩阵了，当然每个 $M_i(x)$
是不一样的.最后写成矩阵形式为: $$M_i(x) = \left[ \begin{matrix} \exp\left\{\sum_{k=1}^K w_k f_k(s_1,s_1,x,i)\right\}, \exp\left\{\sum_{k=1}^K w_k f_k(s_1,s_2,x,i)\right\},\cdots,\exp\left\{\sum_{k=1}^K w_k f_k(s_1,s_m,x,i)\right\} \\ \exp\left\{\sum_{k=1}^K w_k f_k(s_2,s_1,x,i)\right\}, \exp\left\{\sum_{k=1}^K w_k f_k(s_2,s_2,x,i)\right\},\cdots,\exp\left\{\sum_{k=1}^K w_k f_k(s_2,s_m,x,i)\right\} \\ \vdots,\vdots,,\vdots \\ \exp\left\{\sum_{k=1}^K w_k f_k(s_m,s_1,x,i)\right\}, \exp\left\{\sum_{k=1}^K w_k f_k(s_m,s_2,x,i)\right\},\cdots,\exp\left\{\sum_{k=1}^K w_k f_k(s_m,s_m,x,i)\right\} \end{matrix} \right]_{m*m}$$

其中的 $s_1,s_2,\cdots,s_m$ 为 $y_{i-1},y_i$ 所有可能的取值状态. 可以看到是不是有点类似 HMM 的转移矩阵？只不过这里的“转移概率”是按所有的特征函数算出的.

这样，给定观测序列 $x$，标记序列 $y$ 的非规范化概率可以通过 $n+1$ 个矩阵的乘积 $\prod_{i=1}^{n+1} M_i(y_{i-1},y_i | x)$ 表示，于是，条件概率 $P_{\boldsymbol{w}}(y|x)$ 是:

$$P_{\boldsymbol{w}}(y|x) = \frac{1}{Z_{\boldsymbol{w}}(x)} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i | x)$$
其中，$Z_{\boldsymbol{w}}(x)$ 为规范化因子，是 $n+1$ 个矩阵的乘积的 (start,stop) 元素: $$Z_{\boldsymbol{w}}(x) = (M_1(x) M_2(x) \cdots M_{n+1}(x))$$
注意，$y_0 = start$ 与 $y_{n+1} = stop$ 表示开始状态与终止状态，规范化因子 $Z_{\boldsymbol{w}}(x)$ 是以 start 为起点 stop 为终点通过状态的所有路径 $y_1 y_2 \cdots y_n$ 的非规范化概率 $\prod_{i=1}^{n+1} M_i(y_{i-1},y_i | x)$ 之和.

---

矩阵形式不太好理解，这里给出一个例子来说明: 给定一个线性链条件随机场，观察序列 $x$，状态序列 $y$，$i = 1,2,3$，$n = 3$，标记 $y_i \in \{1,2\}$，假设 $y_0 = start = 1,y_4 = stop = 1$，各个位置的随机矩阵 $M_1(x),M_2(x),M_3(x),M_4(x)$ 分别是

$$M_1(x) = \left[ \begin{matrix} a_{01},a_{02} \\ 0,0 \end{matrix} \right],\\ M_2(x) = \left[ \begin{matrix} b_{11},b_{12} \\ b_{21},b_{22} \end{matrix} \right],\\ M_3(x) = \left[ \begin{matrix} c_{11},c_{12} \\ c_{21},c_{22} \end{matrix} \right],\\ M_4(x) = \left[ \begin{matrix} 1,0 \\ 1,0 \end{matrix} \right]$$

试求状态序列 $y$ 以 start 为起点 stop 为终点所有路径的非规范化概率及规范化因子.

解：首先计算从 start 到 stop 对应于 $y = (1,1,1),y = (1,1,2),\cdots,y = (2,2,2)$

若以 $y = (1,1,2)$ 为例来说明:
首先加上 start 和 stop 状态，$y$ 序列变成 $y = (1,1,1,2,1)$，于是 $M_1(x)$ 考虑从状态 1 转换到状态 1，$M_2(x)$ 考虑从状态 1 转换到状态 1，$M_3(x)$ 考虑从状态 1 转换到状态 2，$M_4(x)$ 考虑从状态 2 转换到状态 1；于是概率连乘得

$$M_1(x)[1,1] \times M_2(x)[1,1] \times M_3(x)[1,2] \times M_4(x)[2,1] = a_{01}*b_{11}*c_{12}*1$$

于是各路径的非规范化概率分别是:

$$a_{01}b_{11}c_{11},\quad a_{01}b_{11}c_{12},\quad a_{01}b_{12}c_{21},\quad a_{01}b_{12}c_{22} \\ a_{02}b_{21}c_{11},\quad a_{02}b_{21}c_{12},\quad a_{02}b_{22}c_{21},\quad a_{02}b_{22}c_{22}$$

规范化因子 $Z(x)$ 通过计算矩阵乘积 $M_1(x) M_2(x) M_3(x) M_4(x)$ 可知，为所有路径的非规范化概率之和

$$a_{01}b_{11}c_{11} + a_{01}b_{11}c_{12} + a_{01}b_{12}c_{21} + a_{01}b_{12}c_{22} + a_{02}b_{21}c_{11} + a_{02}b_{21}c_{12} + a_{02}b_{22}c_{21} + a_{02}b_{22}c_{22}$$

---

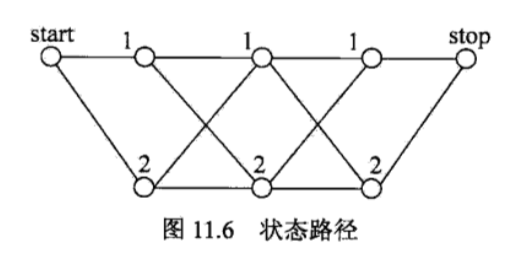
条件随机场的概率计算问题

同隐马尔科夫模型一样，引进前向-后向向量，去计算 $P(Y_i = y_i | x),P(Y_{i-1} = y_{i-1} | x)$ 以及相应的数学期望问题.

前向-后向算法

对每个指标 $i = 0,1,\cdots,n+1$，定义前向向量 $\boldsymbol{\alpha}_i(x)$:

$$\boldsymbol{\alpha}_0(y|x) = \begin{cases} 1,& y = start \\ 0, & 否则 \end{cases}$$

递推公式为

$$\boldsymbol{\alpha}_i^T(y_i | x) = \boldsymbol{\alpha}_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i | x),i = 1,2,\cdots,n+1$$ 又可表示为 $$\boldsymbol{\alpha}_i^T(x) = \boldsymbol{\alpha}_{i-1}^T (x) M_i(x)$$

$\boldsymbol{\alpha}_i(y_i | x)$ 表示在位置 $i$ 的标记是 $y_i$ 并且到位置 $i$ 的前部分标记序列的非规范化概率，$y_i$ 可取的值有 $m$ 个，所以 $\boldsymbol{\alpha}_i(x)$ 是 $m$ 维列向量.

同样，对每个指标 $i = 0,1,\cdots,n+1$，定义后向向量 $\boldsymbol{\beta}_i(x)$ :

$$\boldsymbol{\beta}_{n+1}(y_{n+1}|x) = \begin{cases} 1, & y_{n+1} = stop \\ 0,& 否则 \end{cases}$$

递推公式为

$$\boldsymbol{\beta}_i(y_i|x) = M_i(y_i,y_{i+1}|x) \boldsymbol{\beta}_{i+1}(y_{i+1}|x)$$ 则又可表示为 $$\boldsymbol{\beta}_i(x) = M_{i+1}(x) \boldsymbol{\beta}_{i+1}(x)$$

$\boldsymbol{\beta}_i(y_i | x)$ 表示在位置 $i$ 的标记为 $y_i$ 并且从 $i+1$ 到 $n$ 的后部分标记序列的非规范化概率.

由前向-后向向量定义不难得到:

$$Z(x) = \boldsymbol{\alpha}_n^T(x) \cdot \boldsymbol{1} = \boldsymbol{1}^T \cdot \boldsymbol{\beta}_1(x)$$

这里，$\boldsymbol{1}$ 是元素均为 1 的 m 维列向量.

---

概率计算

按照前向-后向向量的定义，很容易计算标记序列在位置 $i$ 是标记 $y_i$ 的条件概率和在位置 $i-1$ 与 $i$ 是标记 $y_{i-1}$ 和 $y_i$ 的条件概率:

$$P(Y_i = y_i|x) = \frac{\alpha_i^T(y_i|x) \beta_i(y_i|x)}{Z(x)} \\ P(Y_{i-1} = y_{i-1},Y_i = y_i|x) = \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x) \beta_i(y_i|x)}{Z(x)}$$ 其中， $$Z(x) = \alpha_n^T(x) \cdot \boldsymbol{1}$$

这里与 HMM 中的类似，$M_i(y_{i-1},y_i|x)$ 相当于转移矩阵，由于 $M_i(y_{i-1},y_i|x)$ 是由所有转移特征和状态特征计算出来的，状态特征的计算就包含了观测序列 $X$的信息，所以 $P(Y_{i-1} = y_{i-1},Y_i = y_i|x)$ 式的分子就没有 类似于 HMM 中的 $b_j(o_{t+1})$ 这项.

---

期望值的计算

利用前向-后向向量，可以计算特征函数关于联合分布 $P(X,Y)$ 和条件分布 $P(Y|X)$ 的数学期望.

特征函数 $f_k$ 关于条件分布 $P(Y|X)$ 的数学期望是

$$\begin{array} & E_{P(Y|X)}[f_k] &=& \sum_y P(y|x) f_k(y,x) \\&=& \sum_{i=1}^{n+1}\sum_{y_{i-1},y_i} \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)} \end{array}$$
其中，$k = 1,2,\cdots,K$， $$Z(x) = \alpha_n^T(x) \cdot \boldsymbol{1}$$

假设经验分布为 $\hat{P}(X)$，特征函数 $f_k$ 关于联合分布 $P(X,Y)$ 的数学期望是

$$\begin{array} & E_{P(X,Y)}[f_k] &=& \sum_{x,y} P(x,y) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \\&=& \sum_{x} \left( \left( \hat{P}(x)\sum_{y} P(y|x) \right) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \right) \\&=& \sum_x \hat{P}(x) \sum_{i=1}^{n+1} \sum_{y_{i-1},y_i} f_k(y_{i-1},y_i,x,i) \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)} \end{array}$$
其中，$k = 1,2,\cdots,K$， $$Z(x) = \alpha_n^T(x) \cdot \boldsymbol{1}$$

上两式是特征函数数学期望的一般计算公式.对于转移特征 $t_k(y_{i-1},y_i,x,i),k = 1,2,\cdots,K_1$，可以将式中的 $f_k$ 换成 $t_k$；对于状态特征，可以将式中的 $f_k$ 换成 $s_i$，表示为 $s_l(y_i,x,i),k = K_1+l,l = 1,2,\cdots,K_2$ .

通过概率计算和期望值计算公式，对于给定的观测序列 $x$ 与标记序列 $y$，可以通过一次前向扫描计算 $\alpha_i$ 及 $Z(x)$，通过一次后向扫描计算 $\beta_i$，从而计算所有的概率和特征的期望.

---

条件随机场的学习算法

条件随机场的学习算法常用的有迭代尺度法或改进的迭代尺度法，还有拟牛顿法。

笔者看过的实现中，拟牛顿法用的比较多，特别是 L-BFGS 算法，所下面列出拟牛顿法的算法过程，具体算法原理可参考前面的牛顿法与拟牛顿法 一章.

对于条件随机场模型:

$$P_w(y|x) = \frac{\exp{\sum_{i=1}^n w_if_i(x,y)}}{\sum_y \exp{\sum_{i=1}^n w_if_i(x,y)}}$$

学习的优化目标函数是:

$$\min_{w \in R^n} f(w) = \sum_x \hat{P}(x) \log{\sum_y \exp{\sum_{i=1}^n w_i f_i(x,y)}} - \sum_{x,y} \hat{P}(x,y) \sum_{i=1}^n w_i f_i(x,y)$$

其梯度函数是:

$$g(w) = \sum_{x,y} \hat{P}(x) P_w(y|x)f(x,y) - E_{\hat{P}}(f)$$

拟牛顿法的 BFGS 算法如下:

输入：特征函数 $f_1,f_2,\cdots,f_n$；经验分布 $\hat{P}(X,Y)$
输出：最优参数值 $\hat{w}$；最优模型 $P_{\hat{w}}(y|x)$

1. 选定初始点 $w^{(0)}$，取 $\boldsymbol{B}_0$ 为正定对称矩阵，置 $k=0$

2. 计算 $\boldsymbol{g}_k = g(w^{(0)})$. 若 $g_k = 0$，则停止计算；否则转第 3 步.

3. 由 $\boldsymbol{B}_k \boldsymbol{p}_k = -\boldsymbol{g}_k$ 求出 $\boldsymbol{p}_k$

4. 一维搜索: 求 $\lambda_k$ 使得

   $$f(w^{(k)} + \lambda_k \boldsymbol{p}_k) = \min_{\lambda \geq 0} f(w^{(k)} + \lambda_k \boldsymbol{p}_k)$$

5. 置 $w^{(k+1)} = w^{(k)} + \lambda_k \boldsymbol{p}_k$

6. 计算 $\boldsymbol{g}_{k+1} = g(w^{(k+1)})$ ，若 $\boldsymbol{g}_k = 0$，则停止计算；否则，按下式求出 $\boldsymbol{B}_{k+1}$:

   $$\boldsymbol{B}_{k+1} = \boldsymbol{B}_{k} + \frac{y_ky_k^T}{y_k^T \delta_k} - \frac{\boldsymbol{B}_k \delta_k \delta_k^T \boldsymbol{B}_k}{\delta_k^T \boldsymbol{B}_k \delta_k}$$
   其中， $$y_k = \boldsymbol{g}_{k+1} - \boldsymbol{g}_k,\delta_k = w^{(k+1)} - w^{(k)}$$

7. 置 $k = k+1$，转第 3 步.

---

条件随机场的预测算法

同 HMM 一样，我们使用 Viterbi算法进行预测。

首先根据条件随机场的定义，预测问题的目标可以改为:

$$\max_y (\boldsymbol{w} \cdot \boldsymbol{F}(y,x))$$

这里，路径表示标记序列，其中

$$\boldsymbol{w} = (w_1,w_2,\cdots,w_K)^T \\ \boldsymbol{F}(y,x) = (f_1(y,x),f_2(y,x),\cdots,f_K(y,x))^T \\ f_k(y,x) = \sum_{i=1}^n f_k(y_{i-1},y_i,x,i),k = 1,2,\cdots,K$$

注意，这时只需计算非规范化概率，而不必计算概率，可以大大提高效率.为了求解最优路径，将上式目标又可以改下成:

$$\max_y \sum_{i=1}^n \boldsymbol{w} \boldsymbol{F}_i(y_{i-1},y_i,x)$$ 其中， $$\boldsymbol{F}_i(y_{i-1},y_i,x) = (f_1(y_{i-1},y_i,x,i),(f_2(y_{i-1},y_i,x,i),\cdots,(f_K(y_{i-1},y_i,x,i))^T$$ 是局部特征向量.

---

下面叙述维特比算法，首先求出位置 $1$ 的各个标记 $j = 1,2,\cdots,m$ 的非规范化概率:

$$\delta_1(j) = \boldsymbol{w} \boldsymbol{F}_1(y_0 = start,y_1 = j,x),j = 1,2,\cdots,m$$ 一般地，由递推公式，求出到位置 $i$ 的各个标记 $l = 1,2,\cdots,m$ 的非规范化概率的最大值，同时记录非规范化概率最大值的路径 $$\delta_i(l) = \max_{1 \leq j \leq m} \left\{ \delta_{i-1}(j) + \boldsymbol{w} \boldsymbol{F}_i(y_{i-1} = j,y_i = l,x) \right\} \\ \Psi_i(l) = \arg \ \max_{1 \leq j \leq m} \left\{ \delta_{i-1}(j) + \boldsymbol{w} \boldsymbol{F}_i(y_{i-1} = j,y_i = l,x) \right\}$$

其中，$l = 1,2,\cdots,m$， 直到 $i = n$ 时终止. 这时求得非规范化概率的最大值为

$$\max_y(\boldsymbol{w} \cdot \boldsymbol{F}(y,x)) = \max_{1 \leq j \leq m} \delta_n(j)$$ 及最优路径的终点: $$y^*_n = \arg \ \max_{1 \leq j \leq m} \delta_n(j)$$
由此最优路径终点返回， $$y^*_i = \Psi_{i+1}(y^*_{i+1}),i = n-1,n-2,\cdots,1$$
求得最优路径 $y^* = (y^*_1,y^*_2,\cdots,y^*_n)^T$

---

输入: 模型特征向量 $\boldsymbol{F}(y,x)$ 和权值向量 $\boldsymbol{w}$，观测序列 $\boldsymbol{x} = (x_1,x_2,\cdots,x_n)$；
输出: 最优路径 $\boldsymbol{y}^* = (y^*_1,y^*_2,\cdots,y^*_n)$

1. 初始化
   

   $$\boldsymbol{\delta}_1(j) = \boldsymbol{w} \cdot \boldsymbol{F}_1(y_0 = start,y_1 = j,x),j = 1,2,\cdots,m$$

2. 递推. 对 $i = 2,3,\cdots,n$
   

   $$\delta_i(l) = \max_{1 \leq j \leq m} \left\{ \delta_{i-1}(j) + \boldsymbol{w} \boldsymbol{F}_i(y_{i-1} = j,y_i = l,x) \right\} \\ \Psi_i(l) = \arg \ \max_{1 \leq j \leq m} \left\{ \delta_{i-1}(j) + \boldsymbol{w} \boldsymbol{F}_i(y_{i-1} = j,y_i = l,x) \right\}$$ 其中，$l = 1,2,\cdots,m$

3. 终止.
   

   $$\max_{y}(\boldsymbol{w} \cdot \boldsymbol{F}(y,x)) = \max_{1 \leq j \leq m} \boldsymbol{\delta}_n(j)$$

4. 返回路径
   

   $$y^*_i = \Psi_{i+1}(y^*_{i+1}),i = n-1,n-2,\cdots,1$$ 求得最优路径 $\boldsymbol{y}^* = (y^*_1,y^*_2,\cdots,y^*_n)$

---

R 版 CRF 使用

• https://github.com/brianfaires/CRF

• https://github.com/wulingyun/CRF

---

java 源码分析

为分析 CRF 的实现过程，我们使用 github: https://github.com/asher-stern/CRF 的源码，该工程实现了基于CRF的标注，比如词性标注、命名实体识别等。

由于该工程没有提供数据集，所以运行不了，不过也是可以直接去从程序入口开始分析。该工程的大致流程笔者整理如下：

• 读取数据集

  生成 Iterable<List<TaggedToken<K, G>>> corpus 列表对象，其中每一个 List<TaggedToken<K, G>> 表示一条句子，句子中的每个 TaggedToken<K, G> 表示一个单词实体，单词实体的 K 表示 token，一般就是单词字符串了，G 表示标注，如果是词性标注，那就是表示词性标注体系里的标签了。
  由于项目中读取语料库比较复杂，我们可以直接跳过，若要应用自己的项目中，可以替换为自己语料库的解析。

• 生成 CRF 的特征函数

  把语料库中每个标注与对应的观察值作为状态特征，把前一个标注转移到当前标注，作为转移特征。统计完成后可以做一些过滤，比如特征数量出现次数特别少的过滤掉等等。

• 训练各个特征函数的权重

  使用 L-BFGS 拟牛顿法训练各个特征函数的权重，结合标注集与特征函数集，构成 CRF 完整的模型。

• 测试语料标注评估

  使用 Viterbi 算法对新句子进行解码，预测出最有可能的标注序列。

---

程序入口为 com.asher_stern.crf.postagging.demo.TrainAndEvaluate.java 的 main() 方法：

public static void main(String[] args) {
    //传入语料库路径、训练集大小、测试集大小、模型保存路径
    new TrainAndEvaluate(args[0], Integer.parseInt(args[1]), testSize, loadSaveDirectoryName).go();
}

在 go() 方法中做模型训练和测评：

public void go() {
    //加载语料库
    TrainTestPosTagCorpus<String, String> corpus = createCorpus();
    //用训练数据集去训练模型
    PosTagger posTagger = train(corpus.createTrainCorpus());
    //用测试语料集去评估模型
    AccuracyEvaluator evaluator = new AccuracyEvaluator(corpus.createTestCorpus(), posTagger);
    evaluator.evaluate();
}

加载语料库所得到的数据格式在上面介绍项目流程时已经说了，我们直接看训练部分。

private PosTagger train(Iterable<? extends List<? extends TaggedToken<String, String>>> corpus) {
    //创造训练器，构造特征函数
    CrfPosTaggerTrainer trainer = new CrfPosTaggerTrainerFactory().createTrainer(corpusAsList);
    //此时 trainer 已生成特征函数 and 过滤集
    trainer.train(corpusAsList);
    if (loadSaveDirectoryName != null) {
        File saveDirectory = new File(loadSaveDirectoryName);
        //保存训练好的模型
        trainer.save(saveDirectory);
    }
}

从上面的理论部分可知，CRF模型的核心就是特征函数的构造，这个项目中特征函数的构造比较简单，不过从实现过程我们可以更深入的理解特征函数是如何构造的，以及如何优化。因此我们源码分析重点就分析下特征函数的构造，而训练部分就比较常规了，使用 L-BFGS 算法，可以参考 《拟牛顿法》 进行学习。

public CrfPosTaggerTrainer createTrainer(List<List<? extends TaggedToken<String, String>>> corpus) {
    CrfTrainerFactory<String, String> factory = new CrfTrainerFactory<String, String>();
    // 创造训练器，训练器里去构造特征函数
    CrfTrainer<String, String> crfTrainer = factory.createTrainer(corpus,
                (Iterable<? extends List<? extends TaggedToken<String, String>>> theCorpus,
                        Set<String> tags) -> new StandardFeatureGenerator(theCorpus, tags),
                new StandardFilterFactory());
    //训练器与标注器互持引用
    CrfPosTaggerTrainer trainer = new CrfPosTaggerTrainer(crfTrainer);
    return trainer;
}

createTrainer() 方法主要是为了构造特征函数，并对里面的一些数据结构进行封装；参数主要有三个，第一个是语料集，第二个是封装的特征函数生成器，第三个是特征函数过滤器。

public CrfTrainer<K, G> createTrainer(List<List<? extends TaggedToken<K, G>>> corpus,
        CrfFeatureGeneratorFactory<K, G> featureGeneratorFactory, FilterFactory<K, G> filterFactory) {
    //传入语料集，Crf特征生成器，过滤器
    CrfTagsBuilder<G> tagsBuilder = new CrfTagsBuilder<G>(corpus);
    //先生成标注集
    tagsBuilder.build();
    CrfTags<G> crfTags = tagsBuilder.getCrfTags();
    CrfFeatureGenerator<K, G> featureGenerator = featureGeneratorFactory.create(corpus, crfTags.getTags());
    // 生成特征函数，包括状态特征和转移特征
    featureGenerator.generateFeatures();
    //包含状态特征和转移特征；状态特征是忽略大小写特征，转移特征是TagTransitionFeature
    Set<CrfFilteredFeature<K, G>> setFilteredFeatures = featureGenerator.getFeatures();
    // 特征函数已生成，做了一个数据结构的封装
    CrfFeaturesAndFilters<K, G> features = createFeaturesAndFiltersObjectFromSetOfFeatures(setFilteredFeatures, filterFactory);
    return new CrfTrainer<K, G>(features, crfTags);
}

从上面的流程可看成，主要是两步：

• 标注集统计
  统计标注集有哪些，每个标注的前后标注有哪些，用于标注转移矩阵的统计生成。

• 特征函数生成
  特征函数包括状态特征、转移特征，分别统计。

public void build() {
    Set<G> tags = new LinkedHashSet<G>();
    Map<G, Set<G>> canPrecede = new LinkedHashMap<G, Set<G>>();
    Map<G, Set<G>> canFollow = new LinkedHashMap<G, Set<G>>();
    //对每句进行处理
    for (List<? extends TaggedToken<?, G>> sentence : corpus) {
        G previousTag = null;
        //对每个单词实体进行处理，包括token、tag
        for (TaggedToken<?, G> taggedToken : sentence) {
            G tag = taggedToken.getTag();
            // Set 集合，统计有多少个不同的标注
            tags.add(tag);
            // tag 的前 tag 为 previousTag
            CrfUtilities.putInMapSet(canPrecede, tag, previousTag);
            // previousTag 的后 tag 为 tag
            CrfUtilities.putInMapSet(canFollow, previousTag, tag);
            previousTag = tag;
        }
    }
    //前向集合与后向集合补全
    addEmptySets(canPrecede, tags);
    addEmptySets(canFollow, tags);
    // crf tags 包含 tag集合，每个tag 可能的前tag 和 后tag 集合
    crfTags = new CrfTags<G>(tags, canFollow, canPrecede);
}

上面统计了所有标注类别，构成集合 tags，每个标注的前向标注集 canPrecede，每个标注的后向标注集 canFollow。据此可以生产标注转移的转移矩阵。

下面看 StandardFeatureGenerator类分析特征函数的构造：

public void generateFeatures() {
    setFilteredFeatures = new LinkedHashSet<CrfFilteredFeature<String, String>>();
    addTokenAndTagFeatures();   //添加所有的状态特征
    addTagTransitionFeatures(); //添加所有的转移特征
}

先是添加状态特征：

private void addTokenAndTagFeatures() {
    //对每条语料进行处理
    for (List<? extends TaggedToken<String, String>> sentence : corpus) {
        //对每个单词实体进行处理
        for (TaggedToken<String, String> taggedToken : sentence) {
            //从观察值到标注构成一条状态特征
            setFilteredFeatures.add(
                new CrfFilteredFeature<String, String>(
                    //这是一条忽略大小写的特征
                    new CaseInsensitiveTokenAndTagFeature(taggedToken.getToken(), taggedToken.getTag()),
                    new CaseInsensitiveTokenAndTagFilter(taggedToken.getToken(), taggedToken.getTag()), true));
        }
    }
}

然后是转移特征：

private void addTagTransitionFeatures() {
    //前后标注转移构成转移特征函数
    for (String tag : tags) {
        //第一个标注由 null 标注转移到当前标注
        setFilteredFeatures.add(
            new CrfFilteredFeature<String, String>(new TagTransitionFeature(null, tag),
            new TwoTagsFilter<String, String>(tag, null), true));
        //前标注转移到当前标注
        for (String previousTag : tags) {
            setFilteredFeatures.add(
                new CrfFilteredFeature<String, String>(
                    //前状态转换到当前状态
                    new TagTransitionFeature(previousTag, tag),
                    new TwoTagsFilter<String, String>(tag, previousTag), true));
        }
    }
}

将状态特征与转移特征合并到一起，构成 CRF模型的特征函数集合；不过按上面这张方法构造特征函数的数量会非常大，我们需要利用一些规则去把不常用的特征或者噪音特征给过滤掉。

后面统计每个特征函数出现次数的时候，可以把出现次数比较小的特征函数给过滤掉，从而优化模型；另外也可以在训练数据完成后，把权值较小的特征函数过滤掉。

---

这几步就可以构造完特征函数，然后 new CrfTrainer<K, G>(features, crfTags); 封装成 CRF训练器，用于后面 CRF 特征函数的权重训练。

训练过程需要注意的是，不同于一般的 L-BFGS 算法，使用的函数是 CRF 模型的势函数，即在源码中 function.value(point) 计算的是势函数的值，计算所有样本的势函数之和，即考虑全局信息。

小结

本文详细分析了 CRF 模型的原理，并结合 java版本的 CRF 做标注问题的源码分析了 CRF 模型实现过程。

CRF 模型训练是为了得到各个特征函数的权值，与特征函数和标注集一起，构成完整的 CRF 模型。

训练的核心就是构造特征函数，因为前面理论部分对特征函数是如何构造的也没讲清楚，不过我们通过代码分析具体实现过程清楚了。后面的模型训练没细讲，读者有兴趣可参看前面的《拟牛顿法》一篇进行分析。

参考

• 《统计学习方法》——李航