时间序列篇

非平稳序列的确定性分析

时间序列的分解

$Wold$分解定理

对于任何一个离散平稳序列过程 $\{x_t\}$，它都可以分解为两个不相关的平稳序列之后，其中一个为确定性的，另一个为随机性的，不妨记作:

$$x_t = V_t + \xi_t$$
式中，$\{V_t\}$为确定性序列；$\{\xi_t\}$为随机序列，且 $\xi_t = \sum_{j=0}^{\infty}{\varphi_j \epsilon_{t-j}}$.它们需要满足如下条件:

1. $\varphi_0 = 1,\sum_{j=0}^{\infty}{\varphi_j^2}$

2. $\{\epsilon_t\} \approx W N(0,\sigma_{\epsilon}^2)$

3. $Cov(V_t,\epsilon_s) = E(V_t \cdot \epsilon_s), \forall t \neq s$

这里，确定性序列和随机序列的概念如下定义:

对任意序列$\{y_t\}$而言，令 $y_t$ 关于 $q$ 期之前的序列值 $\{y_{t-q},y_{t-q-1},\cdots\}$ 作线性回归

$$y_t = \alpha_0 + \alpha_1 y_{t-q} + \alpha_2 y_{t-q-1} + \cdots + \nu_t$$
式中，$\nu_t$为回归残差序列；$Var(v_t) = \tau_q^2$.

---

显然，$\tau_q^2 \leq Var(y_t)$，且随着 $q$ 的增大而增大，也就是说 $\tau_q^2$ 是非减的有界序列，它的大小可以衡量历史信息对现实值的预测精度. $\tau_q^2$ 越小，说明预测得越准确；$\tau_q^2$越大，说明预测得越差.

如果 $\lim_{q \rightarrow \infty}{\tau_q^2} = 0$，说明序列的发展有很强的规律性(或称确定性)，历史数据可以很好地预测将来，这时称 $\{y_t\}$ 是确定性序列.

如果 $\lim_{q \rightarrow \infty}{\tau_q^2} = Var{y_t}$ ，说明序列随着时间的发展随机性很强，历史信息对于现时值的估计或者说是预测效果很差，这时称 $\{y_t\}$ 是随机序列.

显然，针对之前我们对平稳序列进行 $ARMA(p,q)$ 模型拟合时得到的拟合模型

$$x_t = \mu + \frac{\Theta(B)}{\Phi(B)} \epsilon_t$$
其中，$\{\mu_t = \mu,t \in T\}$ 即为确定性平稳序列；$\{\frac{\Theta(B)}{\Phi(B)} \epsilon_t, t \in T\}$ 即为随机平稳序列.而对 $ARMA(p,q)$ 模型的分析实际上主要是对随机平稳序列进行的分析.

---

$Carmer$ 分解定理

$Wold$分解定理是现代时间序列分析理论的灵魂.尽管 $Wold$分解定理只是为了分析平稳序列的构成，但 $Cramer$ 已于1961年证明这种分解思路同样可以用于非平稳序列.

$Carmer$分解定理: 任何一个时间序列 $\{x_t\}$ 都可以分解为两部分的叠加，其中一部分是由多项式决定的确定性趋势成分，另一部分是平稳的零均值误差成分，即

$$x_t = \mu_t + \epsilon_t = \sum_{j=0}^d{\beta_j t^j} + \Psi(B) a_t$$
式中，$d < \infty;\beta_1,\cdots,\beta_d$ 为常数系数；$\{a_t\}$ 为一个零均值白噪声序列；$B$为延迟算子.因为 $$E(\epsilon_t) = \Psi(B) E(a_t) = 0$$ 所以有 $$E(x_t) = E(\mu_t) = \sum_{j=0}^d{\beta_j} t^j$$
即均值序列 $\left\{ \sum_{j=0}^d {\beta_j t^j} \right\}$ 反映了 $\{x_t\}$ 受到的确定性影响，而 $\{\epsilon_t; \epsilon_t = \Psi(B) a_t\}$ 反映了 $\{x_t\}$ 受到的随机影响.

$Cramer$分解定理说明任何一个序列的波动都可以视为同时受到了确定性影响和随机性影响的作用.平稳序列要求这两方面的影响都是稳定的，而非平稳序列产生的机理就在于它所受到的这两方面的影响至少有一方面是不稳定的.

---

确定性因素分析

在自然界中，由确定性因素导致的非平稳通常显示出非常明显的规律性，比如有显著的趋势或者有固定的变化周期，这种规律性信息通常比较容易提取，而由随机因素导致的波动则非常难以确定、分析.根据这种性质，传统的时序分析方法通常都把分析的重点放在确定性信息的提取上，忽视对随机信息的提取，将序列简单地假定为:

$$x_t = \mu_t + \epsilon_t$$ 式中，$\{\epsilon_t\}$ 为零均值白噪声序列.这种分析方法就称为确定性分析方法.

最常用的确定性分析方法是确定性因素分解方法.该方法产生于长期的观察实践.大致可归纳成四大类因素的综合影响:

1. 长期趋势(trend). 该因素的影响会导致序列呈现出明显的长期趋势(递增、递减等).

2. 循环波动(circle). 该因素会导致序列呈现出从低到高再由高至低的反复循环波动.

3. 季节性变化(season). 该因素会导致序列呈现出和季节变化有关的稳定的周期波动.

4. 随机波动(immediate). 除了长期趋势、循环波动和季节性变化之外，序列还会受到各种其他因素的综合影响，而这些影响导致序列呈现出一定的随机波动.

---

在进行确定性时序分析时，我们假定序列会受到这四种因素中的全部或部分的影响，呈现出不同的波动特征.在实务中，常假定这四种因素主要有两种相互作用模式: 加法模型和乘法模型.

1. 加法模型
   

   $$x_t = T_t + C_t + S_t + I_t$$

2. 乘法模型
   

   $$x_t = T_t \cdot C_t \cdot S_t \cdot I_t$$

Durbin 在1975年还介绍过加法与乘法的混合模型，但是一般的统计软件中只提供加法模型和乘法模型的分析程序，混合模型的分析程序只能自编

确定性因素分解方法在宏观经济领域中有广泛的应用，但我们从大量的使用经验中也发现了一些问题.

• 一是如果观察时期不是足够长，那么循环因素和趋势因素的影响很难严格分解开.

• 二是有些经济现象显示出交易日是一个很显著的影响因素，但是在传统因素分解模型中，它却没有被纳入研究.

四大因素的综合影响会导致序列程序出各种变化情况.而我们进行确定性时序分析的目的不外乎以下两种:

• 一是克服其他因素的影响，单纯测度出某一个确定性因素(长期趋势波动或季节效应)对序列的影响

• 二是推断出各种确定性因素彼此之间的相互作用关系以及它们对序列的综合影响.

---

趋势分析

有些时间序列具有非常显著的趋势，有时我们分析的目的就是要找到序列中的这种趋势，并利用这种趋势对序列未来的发展做出合理的预测.

趋势拟合法

趋势拟合法就是把时间作为自变量，相应的序列观察值作为因变量，建立序列值随时间序列的回归模型的方法.根据序列所表现出的线性或非线性特征，拟合方法又可以具体分为线性拟合的曲线拟合.

线性拟合

如果长期趋势呈现出线性特征，那么我们可以用线性模型来拟合

$$\begin{cases} x_t = a + b t + I_t \\ E(I_t) = 0 \\ Var(I_t) = \sigma^2 \end{cases}$$ 式中，$\{I_t\}$为随机波动；$T_t = a + b t$就是消除随机波动的影响之后该序列的长期趋势.

---

以澳大利亚政府 1981-1990 年每季度的消费支出数据(单位: 百万澳元)为例，演示线性拟合:

#读入数据
> x <- c(8444,9215,8879,8990,8115,9457,8590,9294,8997,9574,9051,9724.9120,10143,9746,10074,9578,10817,10116,10779,9901,11266,10686,10961,10121,11333,10677,11325,10698,11624,11052,11393,10609,12077,11376,11777,11225,12231,11884,12109)
#构造时间自变量
> t <- c(1:length(x))
#拟合回归模型
> x.fit <- lm(x ~ t)
#查看拟合信息
> summary(x.fit)
Call:
lm(formula = x ~ t)
Residuals:
   Min     1Q Median     3Q    Max 
-875.9 -306.7   34.8  331.1  818.3 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 8535.620    140.486   60.76   <2e-16 ***
t             91.051      6.122   14.87   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 430.3 on 37 degrees of freedom
Multiple R-squared:  0.8567,    Adjusted R-squared:  0.8528 
F-statistic: 221.2 on 1 and 37 DF,  p-value: < 2.2e-16
> 
> #绘制拟合效果图
> x <- ts(x)
> plot(x)
> abline(lm(x~t),col=2)
>

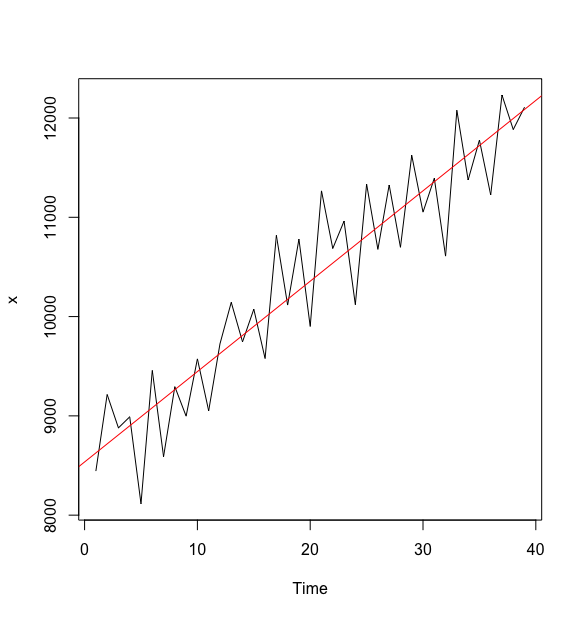
根据模型输出结果，可知澳大利亚政府季度消费支出序列线性拟合模型为:

$$x_t = 8535.620 + 91.051 t + \epsilon_t , \epsilon_t \approx N(0,430.3^2)$$

---

曲线拟合

如果长期趋势呈现出非线性特征，那么我们可以用曲线模型来拟合它.

对曲线模型进行参数估计时，指导思想是: 能转换成线性模型的都转换成线性模型，用线性最小二乘法来进行参数估计；实在不能转换成线性模型的，就用迭代法进行参数估计.

模型	变换	参数估计法
二次型: $T_t = a + bt + c t^2$	令 $t_2 = t^2$，原模型变换为: $T_t = a + bt + ct_2$	线性最小二乘法
指数型: $T_t = a b^t$	对原模型求对数，再令 $T_t' = ln{T_t},a' = ln{a},b' = ln{b}$，原模型变换为: $T_t' = a' + b' t$	用线性最小二乘法求出 $a',b'$，再做变换: $a = e^{a'},b = e^{b'}$
修正指数型: $T_t = a + b c^t$	不能转换成线性模型	迭代法
$Gompertz$型: $T_t = e^{a + b c^t}$	不能转换成线性模型	迭代法
$Logistic$型: $T_t = \frac{1}{a + b c^t}$	不能转换成线性模型	迭代法

R 语言针对非线性趋势的拟合也分为两类: 一类可以写成关于时间 $t$ 的多项式，这时任然可以用 $lm$函数拟合.另一类无法通过适当的变换变成线性回归模型，只能通过非线性回归解决，这时需要调用 $nls$ 函数.

---

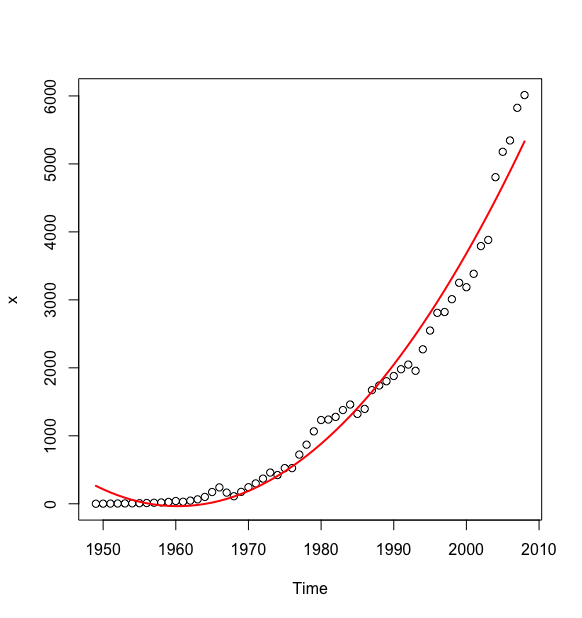
下面以我国 1949-2008 年化肥产量序列进行曲线拟合.

时序图显示该序列有显著的曲线递增趋势，我们尝试使用二次型模型拟合.

#读入数据
> a <- read.table("data/file12.csv",sep = ",",header = T)
> x <- ts(a$output,start = 1949)
#lm 函数拟合
> t1 <- c(1:60)
> t2 <- t1^2
> x.fit1 <- lm(x ~ t1 + t2)
> summary(x.fit1)
Call:
lm(formula = x ~ t1 + t2)
Residuals:
    Min      1Q  Median      3Q     Max 
-532.12 -164.92   24.68  105.51  716.37 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 319.0255   105.3371   3.029  0.00369 ** 
t1          -57.7690     7.9679  -7.250 1.22e-09 ***
t2            2.3551     0.1266  18.601  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 263 on 57 degrees of freedom
Multiple R-squared:  0.9755,    Adjusted R-squared:  0.9746 
F-statistic:  1133 on 2 and 57 DF,  p-value: < 2.2e-16
> 
#nls函数拟合
> x.fit2 <- nls(x~a + b*t1 + c*t1^2 , start = list(a = 1, b = 1, c = 1))
> summary(x.fit2)
Formula: x ~ a + b * t1 + c * t1^2
Parameters:
  Estimate Std. Error t value Pr(>|t|)    
a 319.0255   105.3371   3.029  0.00369 ** 
b -57.7690     7.9679  -7.250 1.22e-09 ***
c   2.3551     0.1266  18.601  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 263 on 57 degrees of freedom
Number of iterations to convergence: 1 
Achieved convergence tolerance: 3.059e-08
> 
#预测结果
> y <- predict(x.fit2)
> y <- ts(y,start = 1949)
> plot(x,type = "p")
> lines(y,col = 2, lwd = 2)
>

---

平滑法

平滑法是进行趋势分析和预测时常用的一种方法.它是利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出变化的规律.它具有调节灵活、计算简便的特征，广泛应用于计量经济、人口研究等诸多领域.根据所用的平滑技术的不同，平滑法又可以分为移动平均法和指数平滑法.

移动平均法

移动平均法的基本思想是对于一个时间序列 $\{X_t\}$ ，我们可以假定在一个比较短的时间间隔里，序列的取值是比较稳定的，它们之间的差异主要是由随机波动造成的.根据这种假定，我们可以用一定时间间隔内的平均值作为下一期的估计值.

$n$ 期移动平均是一种常用的平稳序列预测方法，$\hat{x}_t = \frac{1}{n}(x_t + x_{t-1} + \cdots +x_{t-n+1})$.假定最后一期的观察值为 $x_t$，那么使用 $n$ 期移动平均法，向前预测 $l$ 期，各期的预测值为:

$$\hat{x}_t(1) = \frac{x_t + x_{t-1} + \cdots + x_{t-n+1}}{n} \\ \hat{x}_t(2) = \frac{\hat{x}_t(1) + x_t + \cdots + x_{t-n+2}}{n} \\ \vdots \\ \hat{x}_t(l) = \frac{\hat{x}_t(l-1) + \cdots + \hat{x}_t(1) + x_t + \cdots + x_{t-n+1}}{n}$$
移动平均的期数对原序列的修匀效果影响很大，要确定移动平均的期数，一般会从如下三个方面加以考虑:

1. 事件的发展有无周期性.如果事件的发展具有一定的周期性，一般以周期长度作为移动平均的间隔长度.比如研究每月的平均气温变化趋势，就应该做12期移动平均，通过周期平滑消除季节效应的影响.

2. 对趋势平滑性的要求.一般移动平均的期数越多，修匀曲线越平滑，表现出的长期趋势就越清晰.

3. 对趋势反映近期变化敏感程度的要求.用移动平均方法确定事件的发展趋势都具有一定的滞后性.移动平均的期数越多，滞后性越强；移动平均的期数越少，所得的趋势图对近期变化的反应就越敏感.

综合以上三方面的考虑，如果想得到长期趋势，就应该做期数较多的移动平均，如果想密切关注序列的短期趋势，就应该做期数较少的移动平均.

---

简单指数平滑法

移动平均法实际上就是用一个简单的加权平均数作为某一期趋势的估计值.但在实际生活中，我们会发现对大多数随机事件而言，一般都是近期的结果对现在的影响会大一些，远期的结果对现在的影响会小一些.

为了更好地反映这种影响，我们将考虑时间间隔对事件发展的影响，各期权值随时间间隔的增大而呈指数衰减.这就是指数平滑法的基本思想.

---

$$\hat{x}_t = \alpha x_t + \alpha (1-\alpha) x_{t-1} + \alpha (1-\alpha)^2 x_{t-2} + \cdots$$
式中，$\alpha$为平滑系数，它满足 $0 < \alpha < 1$
因为 $$\hat{x}_{t-1} = \alpha x_{t-1} + \alpha (1 - \alpha) x_{t-2} + \alpha (1-\alpha)^2 x_{t-3} + \cdots$$ 所以 $\hat{x}_t$又等价于 $$\hat{x}_t = \alpha x_t + (1-\alpha)\hat{x}_{t-1}$$
简单指数平滑面临一个确定 $\hat{x}_0$初始值的问题.我们有许多方法可以确定 $\hat{x}_0$的初始值，最简单的方法是指数 $\hat{x}_0 = x_1$.

平滑系数 $\alpha$ 的值由研究人员根据经验给出.一般对于变化缓慢的序列，常取较小的$\alpha$值；相反，对于变化迅速的序列，常取较大的 $\alpha$值.经验表明 $\alpha$值介于 0.05 ~ 0.3 之间，修匀效果比较好.

---

指数平滑也是一种常用的平稳序列预测方法.假定最后一期的观察值为 $x_t$，那么使用指数平滑法，向前预测 1 期的预测值为:

$$\hat{x}_t(1) = \hat{x}_t = \alpha x_t + (1-\alpha)\hat{x}_{t-1} = \alpha x_t + \alpha(1 - \alpha) x_{t-1} + \alpha (1 - \alpha)^2 x_{t-2} + \cdots$$
从理论上我们可以证明使用指数平滑法预测任意 $l$期的预测值都为常数.

证明: 已知 $\hat{x}_t(1) = \hat{x}_t = \alpha x_t + (1-\alpha)\hat{x}_{t-1}$，则

$$\hat{x}_t(2) = \alpha \hat{x}_t(1) + (1-\alpha)\hat{x}_{t-1} = \alpha \hat{x}_t + (1-\alpha) \hat{x_t} = \hat{x}_t$$
任取 $l$ 期，有: $$\hat{x}_t(l) = \alpha \hat{x}_t(l-1) + (1-\alpha)\hat{x}_t(l-1) = \hat{x}_t, l \geq 3$$

所以使用指数平滑最好只做 1 期预测.

---

季节效应分析

在日常生活中，我们可以见到许多有季节效应的时间序列，比如四季的气温、每个月的商品零售额、某自然景点每季度的旅游人数，等等，它们都会呈现出明显的季节变动规律.

我们可以把“季节”广义化，凡是呈现出固定的周期性变化的事件，都称它具有“季节”效应.现在“季节”效应已经变成周期效应的代名词.而“季”也变成了周期内每一期的代名词.

假如没有季节效应的影响，北京市的气温应该始终在某个均值附近随机波动，季节效应的存在使得气温会在不同年份的相同月份呈现出相似的性质.为便于得到数量化的季节信息，我们构造出季节指数的概念.所谓季节指数，就是用简单平均法计算的周期内各时期季节性影响的相对数.

以本例的数据结构为例，我们需要求出每个月的季节指数 $S_1,S_2,\cdots,S_{12}$，那么第 $i$ 年第 $j$ 个月的平均气温可以表示为:

$$x_{ij} = \overline{x} \times S_j + I_{ij} , j = 1,2,\cdots,12$$
式中，$\overline{x}$ 为各月总平均气温；$S_j$ 为第 $j$ 个月的季节指数；$I_{ij}$ 为第 $i$ 年第 $j$ 个月气温的随机波动.

---

季节指数的计算分为三步:

1. 计算周期内各期平均值，得到长期以来该时期的平均水平.假定序列的数据结构为 $m$ 期为一周期，共有 $n$ 个周期.则

   $$\overline{x}_k = \frac{\sum_{i=1}^n{x_{ik}}}{n}, k = 1,2,\cdots,m$$

2. 计算总平均数.

   $$\overline{x} = \frac{\sum_{i=1}^n{\sum_{k=1}^m}{x_{ik}}}{nm}$$

3. 用时期平均数除以总平均数就可以得到各时期的季节指数 $S_k (k = 1,2,\cdots,m)$，即

   $$S_k = \frac{\overline{x}_k}{\overline{x}},k = 1,2,\cdots,m$$

这就是季节指数的构造方法.季节指数反映了该季度与总平均值之间的一种比较稳定的关系.如果这个比值大于 1，就说明该季度的值常常会高于总平均值；如果这个比值小于 1，就说明该季度的值常常低于总平均值；如果序列的季节指数都近似等于 1，那就说明该序列没有明显的季节效应.

---

综合分析

在上面两节里我们分别介绍了单纯的趋势分析方法和单纯的季节效应分析方法.在这一节里主要介绍既有趋势起伏变动，又有季节效应的复杂序列的分析方法.

要对趋势起伏变动和季节效应同时进行分析，首先必须了解他们之间的相互作用关系.但是，通常我们并不知道它们到底是怎样综合作用而影响序列变化的，这时只能根据序列的表现，选择一些经验模型来估计各因素之间的相互作用关系.常用的模型有:

1. 加法模型

   $$x_t = T_t + S_t + I_t$$

2. 乘法模型

   $$x_t = T_t \cdot S_t \cdot I_t$$

式中，$T_t$ 代表序列的长期趋势波动；$S_t$ 代表序列的季节性(周期性)变化；$I_t$代表随机波动.

在确定性影响很强劲时，选择合适的确定性模型通常会得到非常不错的分析预测效果。

R语言中进行确定性因素分解的函数是 decompose，该函数的命令格式如下:

decompose(x, type = )

式中，x表示序列名，type指定了加法模型(type="additive")还是乘法模型(type="multiplicative").

---

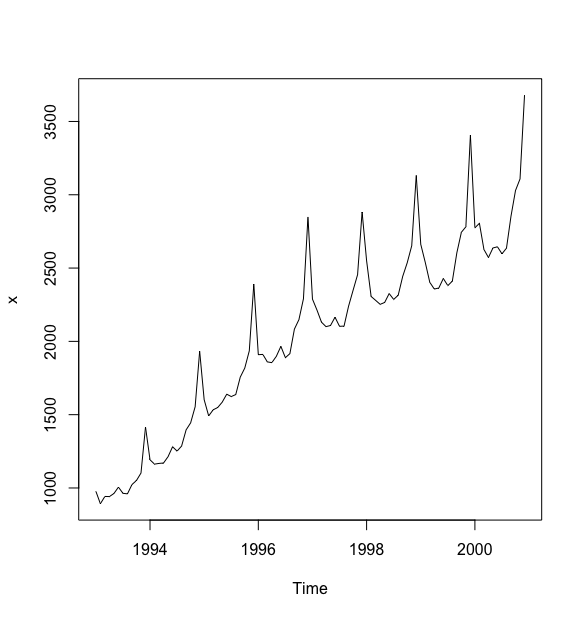
下面对 1993-2000年中国社会消费品零售总额序列进行确定性因素分解.

#读入序列，并绘制时序图
> c <- read.table("data/file14.csv",sep = ",",header = T)
> x <- ts(c$sales,start = c(1993,1),frequency = 12)
> plot(x)
> 

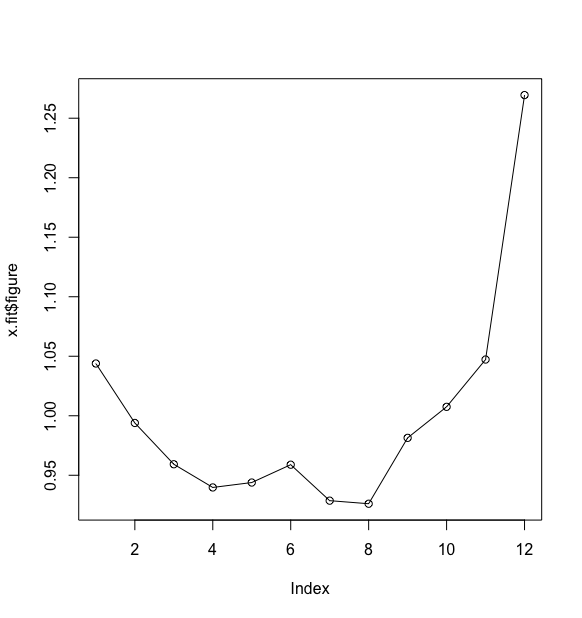
> #确定性因素分解
> x.fit <- decompose(x,type = "mult")
> 
#查看季节指数，并绘制季节指数图
> x.fit$figure
 [1] 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
 [8] 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
> plot(x.fit$figure,type = "o")

#查看所有输出结果
> x.fit
$x
        Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct
1993  977.5  892.5  942.3  941.3  962.2 1005.7  963.8  959.8 1023.3 1051.1
1994 1192.2 1162.7 1167.5 1170.4 1213.7 1281.1 1251.5 1286.0 1396.2 1444.1
1995 1602.2 1491.5 1533.3 1548.7 1585.4 1639.7 1623.6 1637.1 1756.0 1818.0
1996 1909.1 1911.2 1860.1 1854.8 1898.3 1966.0 1888.7 1916.4 2083.5 2148.3
1997 2288.5 2213.5 2130.9 2100.5 2108.2 2164.7 2102.5 2104.4 2239.6 2348.0
1998 2549.5 2306.4 2279.7 2252.7 2265.2 2326.0 2286.1 2314.6 2443.1 2536.0
1999 2662.1 2538.4 2403.1 2356.8 2364.0 2428.8 2380.3 2410.9 2604.3 2743.9
2000 2774.7 2805.0 2627.0 2572.0 2637.0 2645.0 2597.0 2636.0 2854.0 3029.0
        Nov    Dec
1993 1102.0 1415.5
1994 1553.8 1932.2
1995 1935.2 2389.5
1996 2290.1 2848.6
1997 2454.9 2881.7
1998 2652.2 3131.4
1999 2781.5 3405.7
2000 3108.0 3680.0
$seasonal
           Jan       Feb       Mar       Apr       May       Jun       Jul
1993 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1994 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1995 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1996 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1997 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1998 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
1999 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
2000 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
           Aug       Sep       Oct       Nov       Dec
1993 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1994 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1995 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1996 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1997 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1998 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
1999 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
2000 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
$trend
          Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
1993       NA       NA       NA       NA       NA       NA 1028.696 1048.900
1994 1153.913 1179.492 1208.621 1240.533 1275.733 1316.087 1354.700 1385.483
1995 1537.554 1567.687 1597.308 1627.879 1659.350 1694.296 1726.138 1756.412
1996 1890.954 1913.637 1938.921 1966.329 1994.879 2028.796 2063.733 2092.137
1997 2190.733 2207.475 2221.812 2236.637 2251.825 2260.071 2272.325 2287.071
1998 2350.200 2366.608 2383.846 2400.158 2416.213 2434.837 2449.933 2464.292
1999 2513.642 2521.579 2532.308 2547.687 2561.737 2578.554 2594.675 2610.475
2000 2707.971 2726.379 2746.162 2768.446 2793.929 2818.963       NA       NA
          Sep      Oct      Nov      Dec
1993 1069.542 1088.471 1108.496 1130.450
1994 1414.425 1445.429 1476.679 1507.108
1995 1787.517 1813.887 1839.679 1866.312
1996 2116.017 2137.537 2156.521 2173.546
1997 2297.142 2309.683 2322.567 2335.829
1998 2479.100 2488.579 2497.033 2505.433
1999 2630.912 2649.208 2669.550 2689.933
2000       NA       NA       NA       NA
$random
           Jan       Feb       Mar       Apr       May       Jun       Jul
1993        NA        NA        NA        NA        NA        NA 1.0088882
1994 0.9897286 0.9917699 1.0069996 1.0039379 1.0079296 1.0151591 0.9947887
1995 0.9982198 0.9571982 1.0006930 1.0123394 1.0122310 1.0092784 1.0128538
1996 0.9671360 1.0048115 1.0000891 1.0037414 1.0081543 1.0106040 0.9854906
1997 1.0006939 1.0088390 0.9998115 0.9993280 0.9918727 0.9988758 0.9963425
1998 1.0391783 0.9804972 0.9969239 0.9987216 0.9932308 0.9962666 1.0048103
1999 1.0145206 1.0128044 0.9892766 0.9843682 0.9776685 0.9823163 0.9878519
2000 0.9815488 1.0351058 0.9972322 0.9885893 0.9999390 0.9785257        NA
           Aug       Sep       Oct       Nov       Dec
1993 0.9880930 0.9748693 0.9584809 0.9492950 0.9863775
1994 1.0022841 1.0057935 0.9916461 1.0047607 1.0099323
1995 1.0064677 1.0009573 0.9948091 1.0044711 1.0085729
1996 0.9891157 1.0032647 0.9975563 1.0140385 1.0323984
1997 0.9935731 0.9933992 1.0090249 1.0092977 0.9718346
1998 1.0142266 1.0041262 1.0114724 1.0142280 0.9845558
1999 0.9972656 1.0086157 1.0280362 0.9949349 0.9973544
2000        NA        NA        NA        NA        NA
$figure
 [1] 1.0439030 0.9939439 0.9592626 0.9397644 0.9438897 0.9588798 0.9286603
 [8] 0.9260807 0.9814290 1.0074970 1.0472403 1.2694493
$type
[1] "multiplicative"
attr(,"class")
[1] "decomposed.ts"
#查看输出图形
> plot(x.fit)
> 

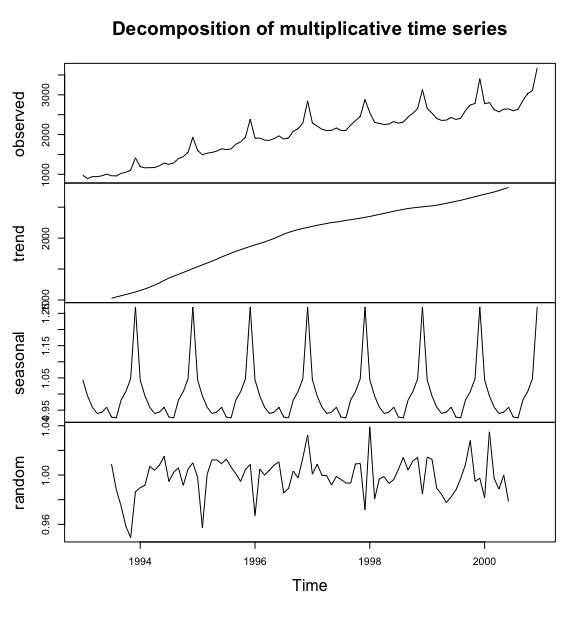
从上面的分解图中可以分别看出 趋势拟合值(x.fit$trend)、季节效应值(x.fit$seasonal)、随机波动值(x.fit$random)

#查看decompose()函数返回的对象
> str(x.fit)
List of 6
 $ x       : Time-Series [1:96] from 1993 to 2001: 978 892 942 941 962 ...
 $ seasonal: Time-Series [1:96] from 1993 to 2001: 1.044 0.994 0.959 0.94 0.944 ...
 $ trend   : Time-Series [1:96] from 1993 to 2001: NA NA NA NA NA ...
 $ random  : Time-Series [1:96] from 1993 to 2001: NA NA NA NA NA ...
 $ figure  : num [1:12] 1.044 0.994 0.959 0.94 0.944 ...
 $ type    : chr "multiplicative"
 - attr(*, "class")= chr "decomposed.ts"
>