回归分析篇

一元线性回归

一元线性回归时描述两个变量之间统计关系的最简单的回归模型。在实际问题中，经常需要研究某一现象与影响它的某一最主要因素的关系。如影响粮食产量的因素非常多，但在众多因素中，施肥量是一个最重要的因素，我们往往需要研究施肥量这一因素与粮食产量之间的关系

一元线性回归虽然简单，但通过一元线性回归模型的建立，可以了解回归分析方法的基本统计思想以及它在实际问题研究中的应用原理

本篇会详细的讲解一元线性回归分析中用到的一些理论基础，如回归系数显著性分析的t检验、F检验等等；最后会举例一个完整的小例子来介绍在实际应用中如何使用一元线性回归分析，并重点详解了R语言中的summary()函数生成的结果的含义

一元回归模型的数学描述

一般情况下，对我们所研究的某个实际问题，获得的n组样本观测值$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$来说，如果它们符合模型$y = \beta_0 + \beta_1 x + \epsilon$，则

$$y_i=\beta_0 + \beta_1 x_i + \epsilon_i,\ \ \ \ \ \ i=1,2,...,n$$
其中 $\epsilon$ 是不可观测的随机误差，它是一个随机变量，通常假定 $\epsilon$ 满足：
$$\begin{cases} E(\epsilon_i) = 0 \\ var(\epsilon_i) = \sigma \end{cases}$$
其中，$i = 1,2,...,n$

通常我们还假定 n 组数据是独立观测的，因而$y_1,y_2,...,y_n$与$\epsilon_1,\epsilon_2,...,\epsilon_n$都是相互独立的随机变量。而$x_i(i = 1,2,...,n)$是确定性变量，其值是可以精确测量和控制的

---

回归分析的主要任务就是通过 $n$ 组样本观测值$(x_i,y_i),i=1,2,...,n$对$\beta_0,\beta_1$进行估计。一般用$\hat{\beta_0},\hat{\beta_1}$分别表示 $\beta_0,\beta_1$ 的估计值，则称

$$\hat{y} = \hat{\beta_0} + \hat{\beta_1}x$$ 为y关于x的一元线性经验回归方程。

由线性方程的几何意义可知，$\hat{\beta_1}$表示经验直线回归方程的斜率，$\hat{\beta_1}$在实际应用中表示自变量 $x$ 每增加一个单位时因变量y的平均增加数量；理解这点，对我们后面在具体的应用场景中解释回归方程所表示的结果，有指导意义

---

在实际的问题中，为了方便对参数作区间估计和假设检验，我们还有假定模型中误差项 $\epsilon$ 遵从正态分布，即

$$\epsilon \approx N(0,\sigma^2)$$
由于 $\epsilon_1,\epsilon_2,...,\epsilon_n$ 是$\epsilon$的独立同分布的样本，因而有 $$\epsilon_i \approx N(0,\sigma^2),\ \ \ \ i = 1,2,...,n$$ 在 $\epsilon_i$ 遵从正态分布的假定下，进一步有随机变量 $y_i$ 也遵从正态分布 $$y_i \approx N(\beta_0 + \beta_1 x_i,\sigma^2),\ \ \ \ i = 1,2,...,n$$

为了以后讨论方便，我们采用矩阵来处理上述表达式，令

$$\boldsymbol{y} = \begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_n \end{bmatrix}$$ $$\boldsymbol{x} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}$$ $$\boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix}$$ $$\boldsymbol{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix}$$
于是模型最终可表示成：
$$\begin{cases} \boldsymbol{y} = \boldsymbol{x} \boldsymbol{\beta} + \boldsymbol{\epsilon} \\ E(\boldsymbol{\epsilon}) = 0 \\ var(\boldsymbol{\epsilon}) = \sigma^2 \boldsymbol{I}_n \end{cases}$$
其中 $\boldsymbol{I}_n$ 为 $n$ 阶单位矩阵.

普通最小二乘估计

为了由样本数据得到回归系数 $\beta_0$ 和 $\beta_1$ 的理想估计值，我们使用普通最小二乘估计(Ordinary Least Square Estimation,OLSE)；普通最小二乘估计具有线性、无偏性等特点

对每一个样本观测值$(x_i,y_i)$，最小二乘法考虑观测值 $y_i$ 与其回归值 $E(y_i) = \beta_0 + \beta_1 x_i$ 的离差越小越好，综合考虑 $n$ 个离差值，定义离差平方和为

$$\begin{eqnarray} Q(\beta_0,\beta_1) &=& \sum_{i=1}^n{(y_i - E(y_i))^2} \tag{2.1} \\ &=& \sum_{i=1}^n{(y_i - \beta_0 - \beta_1 x_i)^2} \tag{2.2} \end{eqnarray}$$

所谓最小二乘法，就是寻找参数 $\beta_0, \beta_1$ 的估计值 $\hat{\beta_0}, \hat{\beta_1}$ ，使上面定义的离差平方和达到极小，即寻找 $\hat{\beta_0}, \hat{\beta_1}$ ，满足

$$\begin{eqnarray} Q(\hat{\beta_0},\hat{\beta_1}) &=& \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{x_i} x_i)^2} \tag{2.3} \\ &=& \min_{\beta_0,\beta_1}{\sum_{i=1}^n{(y_i - \beta_0 - \beta_1 x_i)^2}} \ \ \ \ \ \ \ \ \tag{2.4} \end{eqnarray}$$
依照(2.4)式求出的 $\hat{\beta_0}, \hat{\beta_1}$ 就称为回归参数 $\beta_0, \beta_1$ 的最小二乘估计。称 $$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i$$ 为 $y_i(i = 1,2,...,n)$ 的回归拟合值，简称回归值或拟合值。称 $$e_i = y_i - \hat{y_i}$$ 为 $y_i(i = 1,2,...,n)$ 的残差.

---

根据微积分中求极值的原理，$\hat{\beta_0}, \hat{\beta_1}$ 应满足下列方程组：

$$\begin{cases} \left.\frac{\partial Q}{\partial \beta_0} \right|_{\beta_0 = \hat{\beta_0}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_i)} = 0 \\ \left.\frac{\partial Q}{\partial \beta_1} \right|_{\beta_1 = \hat{\beta_1}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_i)x_i} = 0 \end{cases}$$
经整理后求得 $$\begin{cases} \hat{\beta_0} = \hat{y} - \hat{\beta_1} \overline{x} \\ \hat{\beta_1} = \frac{\sum_{i=1}^n{(x_i - \overline{x})y_i}}{\sum_{i=1}^n{(x_i^2 - n(\overline{x})^2)^2}} \\ \overline{x} = \frac{1}{n}\sum_{i=1}^n{x_i} \\ \overline{y} = \frac{1}{n}\sum_{i=1}^n{y_i} \end{cases}$$

对 $\beta_0, \beta_1$ 的估计方法，还有最大似然估计。最大似然估计是利用总体的分布密度或概率分布的表达式及其样本所提供信息建立起求未知参数估计量的一种方法

有兴趣的读者可以网上百度搜索，如http://blog.csdn.net/yanqingan/article/details/6125812，自行学习了解下

回归方程的显著性检验

通过上述最小二乘法估计出经验回归方程 $\hat{y} = \hat{\beta_0} + \hat{\beta_1}x$ 后，还不能马上用来作分析和预测，因为该经验回归方程是否真正描述了变量y与x之间的统计规律性，还需要运用统计方法对回归方程进行检验

由上面的部分讲到，我们一般假定模型中误差项 $\epsilon$ 遵从正态分布，即

$$\epsilon \approx N(0,\sigma^2)$$ 因此，我们首先要做的就是利用残差分析来做正态性检验，这个正态性假设是基础，其他很多假设检验都是在此基础之上做的；然后是做回归方程的显著性检验，检验是否满足线性规律；然后是做回归系数的显著性检验

这里因为一元线性回归只有一个解释变量，该变量的回归系数显著就代表回归方程显著，所以只需要做回归系数的显著性检验即可

一般回归系数的显著性检验有三种，$t$检验，$F$检验，相关系数检验

$t$ 检验

$t$ 检验是统计推断中常用的一种检验方法，在回归分析中，$t$ 检验用于检验回归系数的显著性

假设的原假设是

$$H_0: \beta_1 = 0$$ 对立假设是 $$H_1: \beta_1 \not= 0$$
回归系数的显著性检验就是要检验因变量y对自变量x的影响程度是否显著。可知如果原假设$H_0$成立，则说明自变量与因变量之间没有真正的线性关系，也就是说自变量x的变化对因变量y并没有影响。

因为在正态性假设下，若原假设 $H_0 : \beta_1 = 0$ 成立，则有，

$$\hat{\beta_1} \approx N(0, \frac{\sigma^2}{L_{xx}})$$
此时 $\hat{\beta_1}$ 在零附近波动，构造 $t$ 统计量 $$t = \frac{\hat{\beta_1}}{\sqrt{\hat{\sigma}^2/L_{xx}}} = \frac{\hat{\beta_1}\sqrt{L_{xx}}}{\hat{\sigma}}$$ 其中 $$L_{xx} = \sum_{i=1}^n{(x_i - \overline{x})^2} = \sum_{i=1}^n{x_i^2} - n(\overline{x})^2$$ 而 $$\hat{\sigma}^2 = \frac{1}{n-2}\sum_{i=1}^n{e_i^2} = \frac{1}{n-2}\sum_{i=1}^n{(y_i - \hat{y_i})^2}$$ 是 $\sigma^2$ 的无偏估计，称 $\hat{\sigma}^2$ 为回归标准差

---

当原假设 $H_0 : \beta_1 = 0$ 成立时，上述构造的 $t$ 统计量服从自由度为$n-2$的$t$分布。给定显著性水平 $\alpha$ ，双侧检验的临界值为 $t_{\alpha/2}$ 。

当 $|t| \geq t_{\alpha/2}$ 时拒绝原假设 $H_0 : \beta_1 = 0$ ，认为$\beta_1$显著不为零，因变量 $y$ 对自变量 $x$ 的一元线性回归成立；当 $|t| \leq t_{\alpha/2}$ 时接受原假设，认为 $\beta_1$ 为零，因变量对自变量的一元线性回归不成立

$F$ 检验

另外一种线性回归方程显著性检验是 $F$ 检验，$F$ 检验是根据平方和分解式，直接从回归效果检验回归方程的显著性

所谓平方和分解式是

$$\sum_{i=1}^n{(y_i - \overline{y})^2} = \sum_{i=1}^n{(\hat{y_i} - \overline{y})^2} + \sum_{i=1}^n{(y_i - \hat{y_i})^2}$$

因为残差的平均值为0，残差以自变量 $x$ 的加权平均值为0

$\begin{cases} \sum_{i=1}^n{e_i} = 0 \\\\ \sum_{i=1}^n{x_ie_i} = 0 \end{cases}$

其中：
$\sum_{i=1}^n{(y_i - \overline{y})^2}$称为总平方和，简记为 $SST$ 或 $S_总$ 或 $L_{yy}$，$SST$ 表示 Sum of Squares for Total.

$\sum_{i=1}^n{(\hat{y_i} - \overline{y})^2}$称为回归平方和，简记为 $SSR$ 或 $S_回$ ，$R$ 表示 Regression.

$\sum_{i=1}^n{(y_i - \hat{y_i})^2}$称为残差平方和，简记为 $SSE$ 或 $S_残$，$E$ 表示 Error.

所以，平方和分解式可以简写为

$$SST = SSR + SSE$$
也可以知道，$SSR$是由回归方程确定，也就是由自变量 $x$ 的波动引起的， $SSE$ 是不能用自变量解释的波动，是由 $x$ 之外的未加控制的因素引起的。

这样，总平方和 $SST$中，能够由自变量解释的部分为 $SSR$ ，不能由自变量解释的部分为 $SSE$ .所以回归平方和$SSR$越大，说明回归的拟合效果越好，因此可以构造 $F$ 统计量：

$$F = \frac{SSR/1}{SSE/(n-2)}$$

---

在正态假设下，当原假设 $H_0 : \beta_1 = 0$ 成立时，$F$ 服从自由度为$(1,n-2)$的 $F$ 分布。当$F$ 值大于临界值$F_\alpha(1,n-2)$时，拒绝$H_0$，说明回归方程显著，$x$ 与 $y$ 有显著的线性关系

也可以通过 $P值$ 来看，所谓P值是$P(F > F_\alpha(1,n-2)) = P_{value}$，一般 $P值 < 0.05$ 就拒绝$H_0$

相关系数的显著性检验

由于一元线性回归方程只涉及到自变量 $x$ 与因变量 $y$ ，所以可以去考察这两者之间的简单相关系数来判断这两者之间的线性关系

设$(x_i,y_i),i=1,2,\cdots,n$是$(x,y)$的n组样本观测值，我们称

$$r = \frac{\sum_{i=1}^n{(x_i - \overline{x})(y_i - \overline{y})}}{\sqrt{\sum_{i=1}^n{(x_i - \overline{x})^2}\sum_{i=1}^n{(y_i - \overline{y})^2}}} = \frac{L_{xy}}{\sqrt{L_{xx}L_{yy}}}$$ 为 $x$ 与 $y$ 的简单相关系数，简称相关系数.

相关系数 $r$ 表示 $x$ 与 $y$ 的线性关系的密切程度，相关系数的取值范围为 $|r| \leq 1$，比较直观的几何图如下所示：

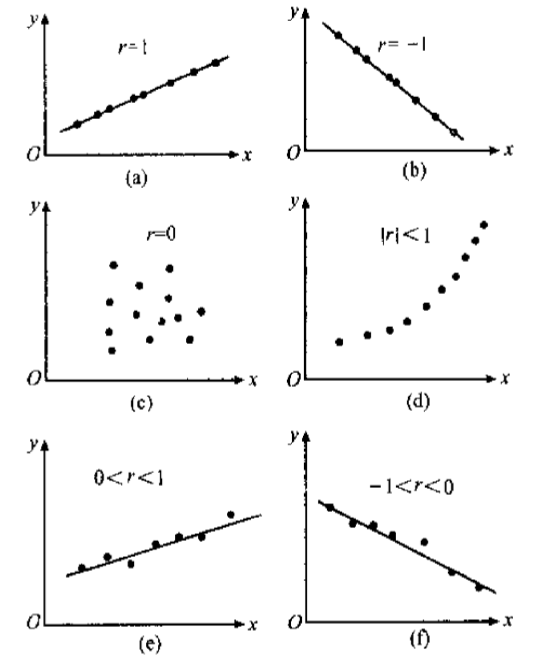
需要指出，相关系数有个明显的缺点，就是它接近于与1的程度与数据组数n有关，这样容易给人一种假象。

当n较小时，相关系数的绝对值更容易接近于1；当n较大时，相关系数的绝对值容易偏小；特别是当 n = 2 时，相关系数的绝对值总为1

因此在样本容量n较小时，仅凭相关系数较大就说变量x与y之间有密切的线性关系，就显得有点草率

样本决定系数

还有一种使用离差平方和分解式的统计量为 $r^2$ ，即把回归平方和与总离差平方和之比定义为样本决定系数：

$$r^2 = \frac{SSR}{SST} = \frac{\sum_{i=1}^n{(\hat{y_i} - \overline{y})^2}}{\sum_{i=1}^n{(y_i - \overline{y})^2}}$$
由关系式$\sum_{i=1}^n{(\hat{y_i} - \overline{y})^2} = \hat{\beta_1}^2\sum_{i=1}^n{(x_i - \overline{x})^2}$可以证明此$r^2$与上述简单相关系数的平方是一样的 $$r^2 = \frac{SSR}{SST} = \frac{L_{xy}^2}{L_{xx}L_{yy}} = (r)^2$$

决定系数 $r^2$ 是一个回归直线与样本观测值拟合优度的相对指标，反映了因变量的波动中能用自变量解释的比例。$r^2$的值总是在0和1之间，也可以用百分比来表示。若$r^2$越接近1，拟合优度就越好，检验越显著

残差分析

一个线性回归方程通过了 $t$ 检验或 $F$ 检验，只是表明变量 x 与 y 之间的线性关系是显著的，或者说线性回归方程式有效的，但是不能保证数据拟合得很好，也不能排除由于意外原因而导致的数据不完全可靠，比如有异常值出现。

只有当与残差项相关的假定满足时，才能放心的运用回归模型

残差与残差图

n 对数据产生n个残差值，即 $e_i = y_i - \hat{y_i}$，残差是实际观察值y与通过回归方程给出的回归值之差，可以看作是误差项 $\epsilon_i$ 的估计值

$$e_i = y_i - \hat{y_i} = y_i - \hat{\beta_0} - \hat{\beta_1}x_i \\ \epsilon_i = y_i - \beta_0 - \beta_1 x_i$$

而以自变量x作横轴，以残差做纵轴，将相应的残差点画在直角坐标系上，就可得到残差图，残差图可以帮助我们队数据质量作一些分析；如下给出了一些常见的残差图：

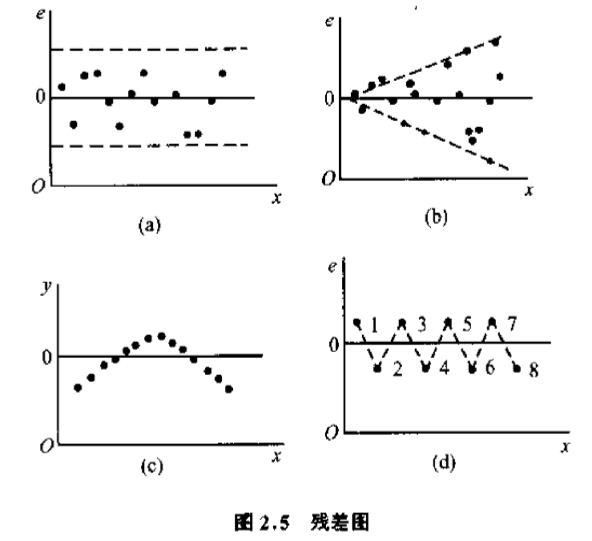
一般认为，如果一个回归模型满足所给出的基本假定，所有残差应是在$e = 0$附近随机变化，并在变化幅度不大的一条带子内。见图(a)的情况。如果残差都落在变化幅度不大的一条带子内，则说明回归模型满足基本假设。

图(b)的情况表明y的观察值的方差并不相同，而是随着x的增加而增加的。这种方差的情况叫做异方差性，专门的处理方法在后面我们讲异方差的处理时再讲。

图(c)中的情况表明y和x之间的关系并非线性关系，而是曲线关系。这就需要考虑用另外的曲线方程去拟合样本观测值y了。另一种可能是y存在自相关。

图(d)的情况称为蛛网线性，表明y具有自相关。

---

残差的性质

关于残差的分析，还与异常值的检测有关系，所以这里介绍一些残差的有关性质

性质1 : $$E(e_i) = 0$$

性质2 : $$var(e_i) = \left[1-\frac{1}{n}-\frac{(x_i - \overline{x})^2}{L_{xx}}\right]\sigma^2 = (1-h_{ii})\sigma^2$$

其中，$h_{ii} = \frac{1}{n} + \frac{(x_i - \overline{x})^2}{L_{xx}}$称为杠杆值。$0<h_{ii}<1$，当$x_i$靠近$\overline{x}$时，$h_{ii}$的值接近0，相应的残差方差就大。当$x_i$远离$\overline{x}$时，$h_{ii}$的值接近1，相应的残差方差就小。

性质3 : 残差满足约束条件: $$\sum_{i=1}^n{e_i} = 0 \\ \sum_{i=1}^n{x_ie_i} = 0$$

这表明残差 $e_1,e_2,\cdots,e_n$是相关的，不是独立的。

改进的残差

在残差分析中，一般认为超过$\pm2\hat{\sigma}$或$\pm3\hat{\sigma}$的残差为异常值，考虑到普通$e_1,e_2,\cdots,e_n$的方差不等，用$e_i$作判断和比较会带来一定的麻烦，人们引入标准化残差和学生化残差的概念，以改进普通残差的性质

标准化残差

$$ZRE_i = \frac{e_i}{\hat{\sigma}}$$

学生化残差

$$SRE_i = \frac{e_i}{\hat{\sigma}\sqrt{1-h_{ii}}}$$

标准化残差使残差具有可比性，$|ZRE_i| > 3$的相应观测值即判定为异常值，这简化了判定工作，但没有解决方差不等的问题。

学生化残差则进一步解决了方差不等的问题，因而在寻找异常值时，用学生化残差优于普通残差，认为$|SRE_i| > 3$的相应观测值为异常值

---

回归系数的区间估计

当我们用最小二乘法得到 $\beta_0,\beta_1$ 的点估计后，在实际应用中往往还希望给出回归系数的估计精度，即给出其置信水平为$1-\alpha$的置信区间。换句话说，就是分别给出以$\hat{\beta_0}$和$\hat{\beta_1}$为中心的一个区间，这个区间以$1-\alpha$的概率包含参数$\beta_0,\beta_1$。置信区间的长度越短，说明估计值$\hat{\beta_0,\hat{\beta_1}}$与$\beta_0,\beta_1$接近的程度越好，估计值就越精确

因为$\hat{\beta_1} \approx N\left(\beta_1,\frac{\sigma^2}{L_{xx}} \right)$可得:

$$t = \frac{\hat{\beta_1 - \beta_1}}{\sqrt{\hat{\sigma^2}/L_{xx}}} = \frac{(\hat{\beta_1} - \beta_1)\sqrt{L_{xx}}}{\hat{\sigma}}$$ 服从自由度为 $n-2$ 的 $t$ 分布，因而有 $$P\left[ \left| \frac{(\hat{\beta_1} - \beta_1)\sqrt{L_{xx}}}{\hat{\sigma}} \right| < t_{\alpha/2}(n-2) \right] = 1-\alpha$$ 上式等价于 $$P\left( \hat{\beta_1} - t_{\alpha/2}\frac{\hat{\sigma}}{\sqrt{L_{xx}}} < \beta_1 < \hat{\beta_1} + t_{\alpha/2}\frac{\hat{\sigma}}{\sqrt{L_{xx}}} \right) = 1-\alpha$$
即得 $\beta_1$ 的置信度为 $1-\alpha$ 的置信区间为 $$\left( \hat{\beta_1} - t_{\alpha/2}\frac{\hat{\sigma}}{\sqrt{L_{xx}}}, \hat{\beta_1} + t_{\alpha/2}\frac{\hat{\sigma}}{\sqrt{L_{xx}}} \right)$$

预测

预测这里我们一般用到的都是单值预测，就是只需要求出预测值就可以了

单值预测

单值预测就是用单个值作为因变量新值的预测值:

$$\hat{y_0} = \hat{\beta_0 + \hat{\beta_1} x_0}$$
此即因变量新值 $y_0 = \beta_0 + \beta_1 x_0 + \epsilon_0$的单值预测

区间预测

因变量新值的区间预测

记

$$h_{00} = \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{L_{xx}}$$ 为新值 $x_0$ 的杠杆值

此区间预测的推导过程跟上面回归系数的区间估计差不多，此时的统计量

$$t = \frac{y_0 - \hat{y_0}}{\sqrt{1+h_{00}}\hat{\sigma}} \approx t(n-2)$$ 可得
$$P \left[ \left| \frac{y_0 - \hat{y_0}}{\sqrt{1+h_{00}}\hat{\sigma}} \right| \approx t_{\alpha/2}(n-2) = 1 - \alpha \right]$$
由此我们可以求得 $y_0$ 的置信概率为 $1-\alpha$ 的置信区间为 $$\hat{y_0} \pm t_{\alpha/2}(n-2)\sqrt{1+h_{00}}\hat{\sigma}$$ 当样本容量 $n$ 较大， $|x_0 - \overline{x}|$ 较小时，$h_{00}$接近零， $y_0$ 的置信度为 95% 的置信区间近似为 $$\hat{y_0} \pm 2\hat{\sigma}$$

因变量新值的平均值的区间估计

由于 $E(y_0) = \beta_0 + \beta_1 x_0$ 是常数，又得

$$\hat{y_0} - E(y_0) \approx N\left(0,\left( \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{L_{xx}} \right)\sigma^2 \right)$$
进而可得置信水平为 $1-\alpha$ 的置信区间为 $$\hat{y_0} \pm t_{\alpha/2}(n-2)\sqrt{h_{00}}\hat{\sigma}$$

R语言程序实例

此示例为了演示如何利用上面的理论在实际项目分析中的应用，这里使用的是R内置的trees数据，其中包含了Volume(体积)、Girth(树围)、Height(树高)这三个变量，我们希望以体积为因变量，树围为自变量进行一元线性回归

模型建立

> head(trees)    #数据源
  Girth Height Volume
1   8.3     70   10.3
2   8.6     65   10.3
3   8.8     63   10.2
4  10.5     72   16.4
5  10.7     81   18.8
6  10.8     83   19.7

> plot(Volume ~ Girth, data = trees, pch = 16, col = "red")    #画出体积与树围的散点图

> model <- lm(Volume ~ Girth, data = trees)    #体积与树围进行一元线性回归

> abline(model, lty = 2)    #将线性回归的结果画在上述散点图上

> summary(model)    #查看回归模型的结果

Call:
lm(formula = Volume ~ Girth, data = trees)

Residuals:
   Min     1Q Median     3Q    Max 
-8.065 -3.107  0.152  3.495  9.587 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -36.9435     3.3651  -10.98 7.62e-12 ***
Girth         5.0659     0.2474   20.48  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.252 on 29 degrees of freedom
Multiple R-squared:  0.9353,    Adjusted R-squared:  0.9331 
F-statistic: 419.4 on 1 and 29 DF,  p-value: < 2.2e-16

> 

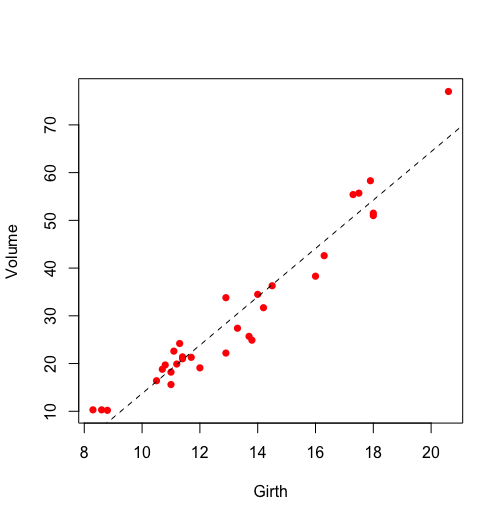
上述代码中，基本的画图部分我们在前面基础篇之绘图中已经详细的讲解过了，这里就不再重复，这里重点讲解下 lm() 函数和 summary(model) 的结果所代表的含义

---

介绍 lm() 函数

lm()函数可以用来做线性回归，做拟合，具体参数介绍可以使用 help("lm") 来查看，该函数的完整形式为:

myfilt <- lm(formula, data, subset, weights, na.action,
method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
singular.ok = TRUE, contrasts = NULL, offset, ...)

其中需要关注的是formula和data两个参数，data参数是一个数据框，包含了用于拟合模型的数据，如上面的例子中的trees就是回归分析所用到的数据源；而formula参数是指要拟合的模型形式；结果对象(如myfit)存储在一个列表中，包含了所拟合模型的大量信息

以下为参数 formula 中的符号的详细解释:

符号	用途	示例
~	分割符号，左边为响应变量，右边为解释变量	x,y,w预测y,代码为 y ~ x + z + w
+	分隔预测变量	y ~ x + z + w
:	表示预测变量的交互项	x,z,x与z的交互项预测y,代码为 y ~ x + z + x:z
*	表示所有可能交互项的简洁方式	y ~ x*z*w可展开为y ~ x + z + w + x:z + x:w + z:w + x:z:w
^	表示交互项达到某个次数	y ~ (x + z + w)^2可展开为 y ~ x + z + w + x:z + x:w + z:w
.	表示包含除因变量外的所有变量	若一个数据框包含变量x,y,z,w,代码y~.可展开为y ~ x + y + w
-	减号，表示从等式中移除某个变量	y ~ (x + z + w)^2 - x:w 可展开为 y ~ x + z + w + x:z + z:w
-1	删除截距项	y ~ x - 1 拟合y在x上的回归，并强制直线通过原点
I()	从算术的角度来解释括号中的元素	y ~ x + (z + w)^2将展开为y ~ x + z + w + z:w 相反，代码y ~ x + I((z + w)^2) 将展开为 y ~ x + h，h是一个由z和w的平方和创建的新变量
function	可以在表达式中用的数学函数	log(y) ~ x + z + w表示通过x,z,w来预测log(y)

---

解释 summary() 的结果

接下来我们详细解释 summary(model) 函数的结果代表的含义:

> summary(model)

Call:
lm(formula = Volume ~ Girth, data = trees)

Residuals:
   Min     1Q Median     3Q    Max 
-8.065 -3.107  0.152  3.495  9.587 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -36.9435     3.3651  -10.98 7.62e-12 ***
Girth         5.0659     0.2474   20.48  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.252 on 29 degrees of freedom
Multiple R-squared:  0.9353,    Adjusted R-squared:  0.9331 
F-statistic: 419.4 on 1 and 29 DF,  p-value: < 2.2e-16

>

Call部分是指出了回归模型的形式，例如本例中是对Volume和Girth用的一元线性回归，数据源为trees

Residuals部分表示的残差，分别给出了残差的最小值，1/4分位数，中位数，3/4分位数，最大值

Coefficients部分表示的是回归系数的结果，每一行代表一个解释变量，如第一行(Intercept)代表了截距项，第二行代表了解释变量Girth的回归系数；而列分别是对应回归系数的估计值、方差、t值、p值、t检验；其中Signif. codes指出，***表示对应回归系数非常显著，**很显著，*显著，.一般，不显著，一般 p值 < 0.05 就是显著

Residual standard error部分表示的是残差的标准误差，例如这里显示在29个自由度上的残差的标准误差为4.252

Multiple R-squared部分和Adjusted R-squared部分表示的是R方和调整的R方，也即是样本决定系数，上面的理论部分也提到了R方的计算公式；R方越接近1越好

F-statistic表示 $F$ 统计量，本例表示 $F$ 服从自由度为 $(1, 31 - 2)$ 的 $F$ 分布，统计量的值为419.4；对应的p-value为 <2.2e-16；上面的理论部分也详细讲解了$F$统计量及$p值$的构造公式

从上例的结果显示中可以看成，回归系数的p值和F统计量可得回归模型是显著的，但从实际的场景考虑，截距项不应该为负数，所以可以修改formula将截距项强制为0，如:

> model2 <- lm(Volume ~ Girth - 1, data = trees)
> 

---

与回归模型结果的提取有关的函数介绍

函数	用途
summary()	展示拟合模型的详细结果
coefficients()	列出拟合模型的模型参数(截距项和斜率)
confint()	提供模型参数的置信区间 (默认95%)
fitted()	列出拟合模型的预测值
residuals()	列出拟合模型的残差值
anova()	生成一个拟合模型的方差分析表，或者比较两个或更多拟合模型的方差分析表
vcov()	列出模型参数的协方差矩阵
AIC()	输出赤池信息统计量
plot()	生成平均拟合模型的诊断图
predict()	用拟合模型对新的数据集预测响应变量值

这些函数的详细信息，可通过help()函数来查看，如 help("predict")

---

模型诊断

在模型建立后会利用各种方式来检验模型的正确性，对残差进行分析是常见的方法，下面我们通过残差分析来进一步诊断该模型:

> par(mfrow=c(2,2))    #将绘图框分成四个区域

> plot(model)    # 画出模型拟合结果

> par(mfrow = c(1,1))
> 

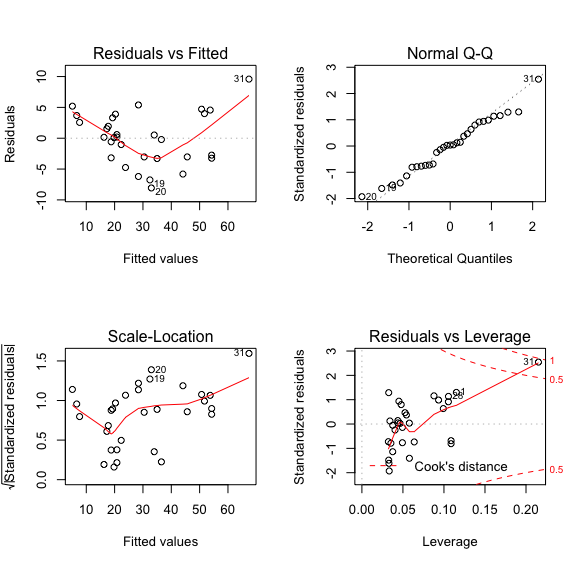
左上图是残差对拟合值作图，整体呈现出一种先下降后上升的模式，显示残差中可能还存在未提炼出来的影响因素；若拟合效果比较好的话，残差对拟合值的图中点的分布应该是随机的，不会出现这种模式

右上图是残差Q-Q图，用以观察残差是否符合正态分布；若残差符合正态分布，这些点应该是分布在虚线附近，大致呈一条直线

左下图是标准化残差对拟合值作图，用于判断模型残差是否等方程

右下图是标准化残差对杠杆值，虚线表示cooks距离等高线；这里我们发现31号样本有较大的影响(异常点)，在虚线的外面

---

变量变换

因为31号样本有着强影响力，为了降低其影响，一种方法就是将变量进行开方变换来改善回归效果，从残差标准误差到残差图，各项观察都说明变换是有效的

> plot(sqrt(Volume) ~ Girth, data = trees, pch = 16, col = 'red')

> model2 <- lm(sqrt(Volume) ~ Girth, data = trees)    #对因变量开方处理

> abline(model2,lty = 2)

> summary(model2)

Call:
lm(formula = sqrt(Volume) ~ Girth, data = trees)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.56640 -0.19429 -0.01169  0.20934  0.65575 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.55183    0.23719  -2.327   0.0272 *  
Girth        0.44262    0.01744  25.385   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2997 on 29 degrees of freedom
Multiple R-squared:  0.9569,    Adjusted R-squared:  0.9555 
F-statistic: 644.4 on 1 and 29 DF,  p-value: < 2.2e-16

> par(mfrow=c(2,2))

> plot(model2)

> par(mfrow = c(1,1))
>

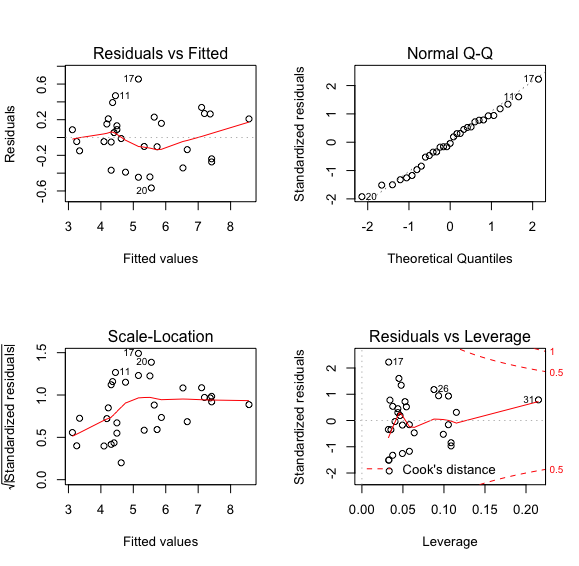
对比未对因变量处理时的回归结果，此时残差标准误差更小，R方更大，F统计量和各回归系数依然显著

从残差分析的图中可以看成，残差与拟合值不具有模式了，Q-Q图检测残差也更符合正态分布了，强影响点也消失了

所以对因变量开方处理时有效的

---

模型预测

下面根据上述模型计算预测值以及置信区间，predict 函数可以获得模型的预测值，加入参数可以得到预测区间

> plot(sqrt(Volume) ~ Girth, data = trees, pch = 16, col = 'red')

> model2 <- lm(sqrt(Volume) ~ Girth, data = trees)

> pre <- predict(model2, interval = 'prediction')    #预测，这里没有指定新值，所以是对模型中已有的点进行预测

> data.pre <- data.frame(pre)

> lines(data.pre$lwr ~ trees$Girth, col = 'blue', lty = 2)    #画预测结果的置信区间下沿

> lines(data.pre$upr ~ trees$Girth, col = 'blue', lty = 2)    #画预测结果的置信区间上沿

> summary(pre)    #查看预测结果的简单统计信息
      fit             lwr             upr       
 Min.   :3.122   Min.   :2.475   Min.   :3.769  
 1st Qu.:4.339   1st Qu.:3.711   1st Qu.:4.967  
 Median :5.158   Median :4.535   Median :5.781  
 Mean   :5.312   Mean   :4.680   Mean   :5.945  
 3rd Qu.:6.198   3rd Qu.:5.571   3rd Qu.:6.826  
 Max.   :8.566   Max.   :7.891   Max.   :9.242  

> pre    #查看预测结果
        fit      lwr      upr
1  3.121955 2.474677 3.769234
2  3.254743 2.610298 3.899187
3  3.343268 2.700621 3.985914
.........
29 7.415412 6.770011 8.060813
30 7.415412 6.770011 8.060813
31 8.566236 7.890543 9.241929
> 

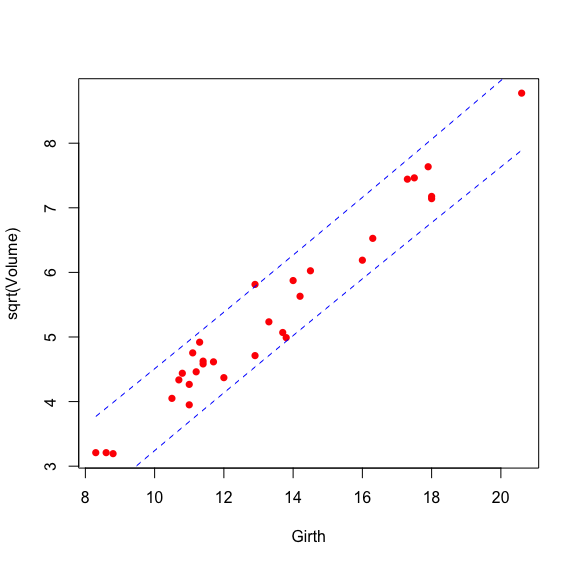
若想考察预测的准确度，可以通过残差平方和等参数来对比:

> sum(residuals(model2)^2)
[1] 2.604755
>