时间序列篇

条件异方差模型

在前面定义 $ARIMA$模型时，都会有这样一个条件$E(\epsilon_t) = 0, Var(\epsilon_t) = \sigma_{\epsilon}^2 , E(\epsilon_t \epsilon_s) = 0, s \neq t$，表示残差零均值、独立、同方差。

其中若 $E(\epsilon_t \epsilon_{t-j}) \neq 0, \exists j \geq 1$ 呢，前面的介绍可知，我们可以尝试残差自回归模型.若 $Var(\epsilon_t) = h(t)$呢，又该如何拟合模型呢？这是我们可以使用本篇要介绍的条件异方差模型来做.

异方差

异方差的影响

使用 $ARIMA$ 模型拟合非平稳序列时，对残差序列有一个重要假定————残差序列 $\{ \epsilon_t \}$ 为零均值白噪声序列.换言之，残差序列要满足如下三个假定条件.

1. 零均值
   $$E(\epsilon_t) = 0$$
2. 纯随机
   $$Cov(\epsilon_t, \epsilon_{t-i}) = 0, \forall i \geq 1$$
3. 方差齐性
   $$Var(\epsilon_t) = \sigma_{\epsilon}^2$$

如果方差齐性假定不成立，即随机误差序列的方差不再是常数，它会随着时间的变化而变化，可以表示为时间的某个函数:

$$Var(\epsilon_t) = h(t)$$ 这种情况称为 异方差.

纯随机假定一直是我们重点监控的对象.如果假定不满足，就说明残差序列中还蕴涵着值得提取的自相关信息.为了有效验证这个假定条件是否成立，统计学家构造了许多适用于不同场合的自相关检验统计量，比如前面介绍的 $Q$ 统计量、$LB$ 统计量、$DW$ 统计量等.

只有第三个假定————方差齐性假定，在此之前我们没有进行任何检验.在缺省检验的情况下就默认残差序列一定满足这个条件.但实际上，这个假定条件并不总是满足的.忽视异方差的存在会导致残差的方差被严重低估，继而参数显著性检验容易犯归纳伪错误.这使得参数的显著性检验失去意义，最终导致模型的拟合精度受影响.为了提高模型拟合的精度，我们需要对残差序列进行方差齐性检验.

---

异方差的直观诊断

残差图

当残差序列 $\{ \epsilon_t \}$ 方差齐性时，它应该在一个边界与均值的距离几乎相等的空间随机波动，不带任何趋势，如下图所示，否则就显示出异方差的性质了.

残差平方图

由于残差序列的方差实际上就是它平方的期望，即

$$Var(\epsilon_t) = E(\epsilon_t^2)$$ 所以残差序列是否方差齐性，主要是考察 $\epsilon_t^2$ 的性质.我们可以借助残差平方图————$\epsilon$ 关于 $t$ 变化的二维坐标图，对残差序列的方差齐性进行直观诊断.

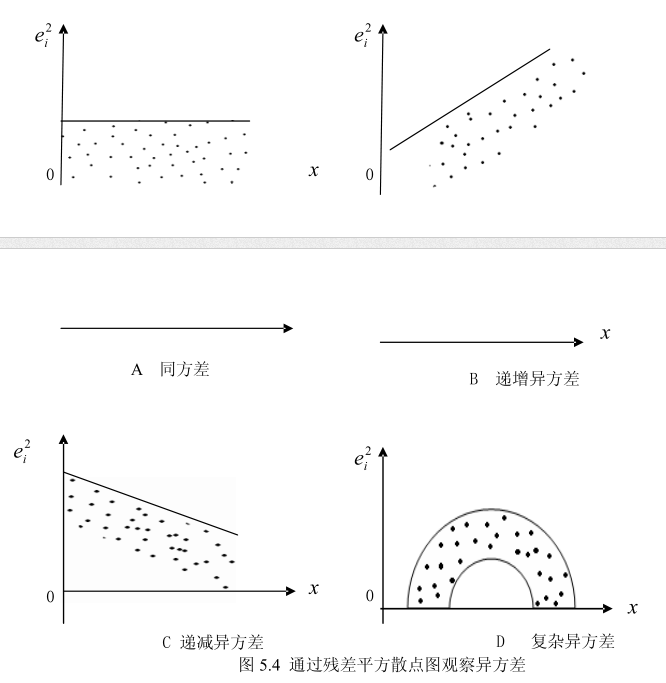
和残差图的判断原则一样，假设方差齐性满足，有

$$E(\epsilon_t^2) = \sigma_{\epsilon}^2$$ 这意味着 $\epsilon_t^2$ 应该在某个常数值 $\sigma_{\epsilon}^2$ 附近随机波动，它不应该具有任何明显的趋势，否则就呈现出异方差性.

---

下面以美国 1963年 4 月至 1971 年 7 月短期国库券的月度收益率序列的例子来说明:

> b <- read.table("data/file21.csv",sep = ",",header = T)
> x <- ts(b$yield_rate,start = c(1963,4),frequency = 12)
> 
> split.screen(c(2,2))  # 将屏幕分割成 2*2 的四块
[1] 1 2 3 4
> 
> screen(1)     # 屏幕 1 预备输出
> plot(x,main = "原始时间序列")
> 
> screen(2)     # 屏幕 2 预备输出
> x.dif <- diff(x)
> plot(x.dif,main = "一阶差分 ")
> 
> screen(3)     # 屏幕 3 预备输出
> plot(x.dif^2,main = "二阶差分")
> 
# dev.off()   #关闭窗口输出设备

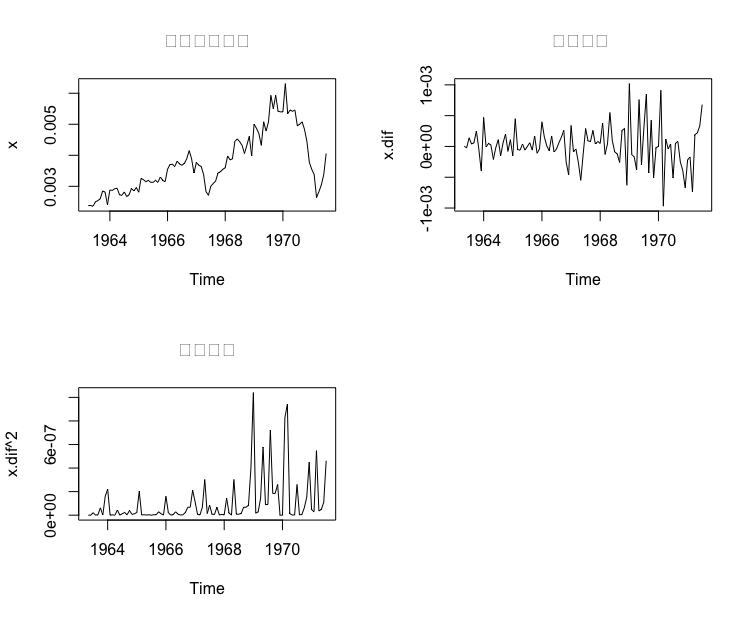
图中时序图显示序列显著非平稳. 1 阶差分后序列显示出均值平稳但方差递增的性质.进一步观察 1 阶差分后残差平方图，可以发现它更加明显地呈现出异方差的特征.

---

当残差序列异方差时，我们需要对它进行进一步的处理，处理思路大致有两种:

1. 假如已知异方差函数具体形式，进行方差齐性变换.

2. 假如不知异方差函数的具体形式，拟合条件异方差模型.

---

方差齐性变换

使用场合

假设序列显示出显著的异方差性，且方差 $\sigma_t^2$ 与均值 $\mu_t$ 之间具有某种函数关系:

$$\sigma_t^2 = h(\mu_t)$$ 式中，$h(\cdot)$ 是某个已知函数.

在这种场合下，我们的处理思路是尝试寻找一个转换函数 $g(\cdot)$ ，使得经转换后的变量 $g(x_t)$ 满足方差齐性:

$$Var(g(x_t)) = \sigma^2$$

转换函数的确定

将 $g(x_t)$ 在 $\mu_t$ 附近做 1 阶泰勒展开:

$$g(x_t) \approx g(\mu_t) + (x_t - \mu_t) g'(\mu_t)$$ 式中，$g'(\cdot)$ 为 $g(\cdot)$ 的 1 阶导数，则 $g(x_t)$ 的方差: $$Var[g(x_t)] \approx Var[g(\mu_t) + (x_t - \mu_t) g'(\mu_t)] \\ = [ g'(\mu_t) ]^2 \cdot Var(x_t) \\ = [ g'(\mu_t) ]^2 h(\mu_t)$$ 显然，要使得 $Var[g(x_t)]$ 等于常数，转换函数的导函数 $g'(\cdot)$ 必须与 $\sqrt{h(\cdot)}$ 具有倒函数关系: $$g'(\mu_t) = \frac{1}{\sqrt{h(\mu_t)}}$$

---

在实际中，许多金融时间序列都呈现出异方差的性质，而且通常序列的标准差与其水平具有某种正比关系，即序列的水平低时，序列的波动范围小，序列水平高时，序列的波动范围大.对于这种异方差的性质，最简单的假定是:

$$\sigma_t = \mu_t$$ 即等价于: $$h(\mu_t) = \mu_t^2$$ 要使得原序列进过适当转换后方差齐性，就必须满足: $$g'(\mu_t) = \frac{1}{h(\mu_t)} = \frac{1}{\mu_t}$$
等价推导出 $$g(\mu_t) = ln(\mu_t)$$
这意味着对于标准差与水平成正比的异方差序列，对数变化可以有效地实现方差齐性.

---

下面任然以美国 1963年 4 月至 1971 年 7 月短期国库券的月度收益率序列使用方差齐性变换方法进行分析:

> split.screen(c(1,2))
[1] 1 2
> 
> screen(1)
> lnx <- log(x)
> plot(lnx,main = "原始序列取对数后")
> 
> screen(2)
> dif.lnx <- diff(lnx)
> plot(dif.lnx,main = "对数转换后的序列差分")
> 
> for(i in 1:2) print(Box.test(dif.lnx,lag = 6*i))
    Box-Pierce test
data:  dif.lnx
X-squared = 3.4118, df = 6, p-value = 0.7557
    Box-Pierce test
data:  dif.lnx
X-squared = 9.8323, df = 12, p-value = 0.6307
>

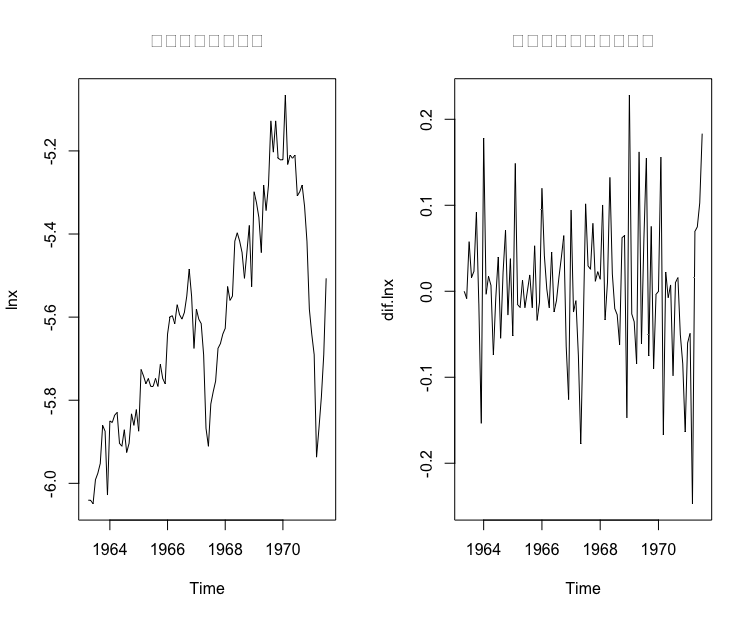
在前面的分析中，我们看到短期国库券收益率序列的波动性与序列值之间具有一定的正相关性，假定它们之间具有正比关系，对原序列进行对数变换.

对数序列时序图显示它保持了原序列的变化趋势.对数序列 1 阶差分后时序图显示残差序列波动较平稳.白噪声检测显示残差序列可视为白噪声序列.这说明通过方差齐性变换，拟合效果不错.我们可以得到该序列的拟合模型为:

$$ln(x_t) = \epsilon_t$$ 式中，$\{\nabla \epsilon_t \}$ 为零均值白噪声序列.

---

条件异方差模型

方差齐性变化为异方差序列的精确拟合提供了一种很好的解决方法，但这种方法只适用于部分异方差波动序列.因为要使用方差齐性变化必须事先知道异方差函数的形式，而这不是对所有的序列都可以做到的.

实践中，我们只能根据残差图及残差平方图所显示出来的特点，使用一些常用的函数形式估计异方差函数.在进行金融世家序列分析时，由于金融序列的标准差与水平之间通常具有某种正相关关系，因此异方差函数经常被假定为:

$$h(\mu_t) = \mu_t^2$$ 这导致对数变换在金融时序分析中普遍采用.

但大量的实践证明这种假定太单一化了，对数变换通常只适用于方差随均值的变化而变化的部分序列.异方差的特征有很多，我们并不能通过对数变换将所有的异方差序列转换为方差齐性序列.条件异方差模型就是一种广泛采用的异方差处理方法.

---

$ARCH$ 模型

集群效应

在宏观经济领域和金融领域，经常可以看到具有如下特征的时间序列: 它们在消除确定性非平稳因素的影响之后，残差序列的波动在大部分时段是平稳的，但会在某些时段波动持续偏大，在某些时段波动持续偏小，呈现出集群效应(volatility cluster)

这里以 1926~1991 年标准普尔500股票价值加权月度收益率序列来演示集群效应的特征:

> k <- read.table("data/file22.csv",sep = ",",header = T)
> x <- ts(k$returns, start = c(1926,1),frequency = 12)
# 收益率时序图
> plot(x)

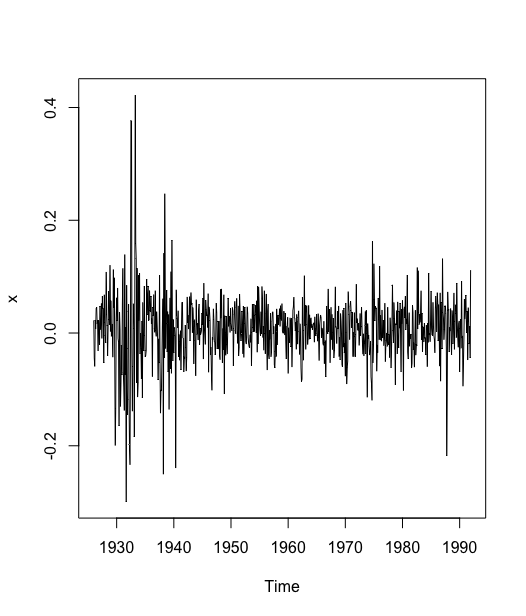
#考察收益率序列平方图
> plot(x^2)
>

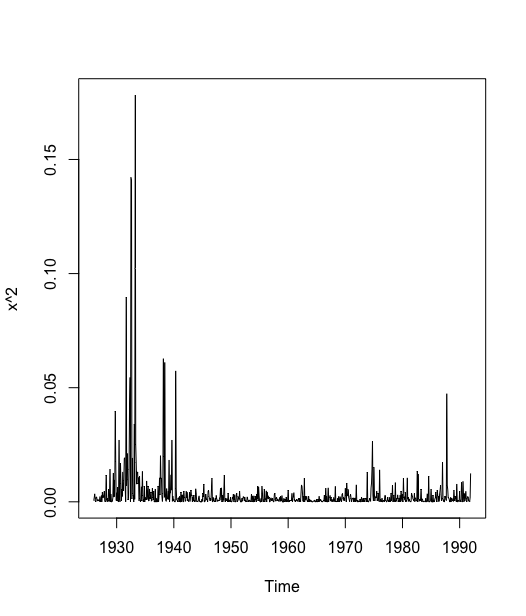
考察该序列时序图.时序图显示该序列没有显著的非平稳特征.序列围绕在零值附近波动，大部分时期波动范围在 (-0.1 ~ 0.1) 之间.但是在一些特殊时段，比如 1930 年前后、1940 年前后、1975 年前后以及 1990 年前后，序列的波动很大.这就是集群效应特征.

我们通常用方差来描述序列的波动，集群效应就意味着在整个序列观察期，序列的方差基本是齐性的，但在某一段或某几段时期方差却显著异于期望方差(例如上图的平方图)，这种序列波动特征给从事利率、汇率、通货膨胀率、股票价格指数等金融时间序列预测的研究人员带来了很大的困扰.他们对这些变量的预测能力因时期的不同而有相当大的差异.

尤其是对于资产持有者而言，它们并不关心资产收益率在所有时间段的综合表现，只关心在他们持有资产的这段时间，资产收益率会不会有大的波动.基于序列全程方差齐性的分析方法无法满足这种需求，这时需要引入条件异方差模型.

---

$ARCH$ 模型的结构

$ARCH模型$的全称为自回归条件异方差模型(autoregressive conditional heteroskedastic)，有时简称条件异方差模型.它是 Engle 于 1982 年在分析英国通货膨胀率序列时提出的残差平方自回归模型.

构造原理为: 假设在历史数据已知的情况下，零均值、纯随机残差序列具有异方差性

$$Var(\epsilon_t) = h_t$$ 在正态分布的假定下，有 $$\epsilon_t / \sqrt{h_t} \approx N(0,1)$$ 异方差等价于残差平方的均值 $$E(\epsilon_t^2) = h_t$$ 使用残差平方序列的自相关系数 $\rho_k = \frac{Cov(\epsilon_t^2,\epsilon_{t-k}^2)}{Var(\epsilon_t^2)}$，可以考察异方差函数的自相关性.

---

考察的结果无外乎如下两种：

1. 自相关系数恒为零，即

   $$\rho_k = 0, k = 1,2,\cdots$$ 这说明异方差函数是纯随机的.此时，历史数据对未来异方差的估计一点作用都没有.这种情况最难分析，至今没有有效的方法能够提取到其中的异方差信息.

2. 存在某个自相关系数不为零，即

   $$\rho_k \neq 0, k \geq 1$$ 这意味着在残差平方序列中蕴含着某种相关信息，可以通过构造适当的模型提取这些相关信息，以获得序列异方差波动特征.$ARCH$模型就是基于这种场合构造的模型.

具有

$$h_t = E(\epsilon_t^2) = \omega + \sum_{j=1}^q \lambda_j \epsilon_{t-j}^2$$ 结构的模型称为 $q$阶自回归条件异方差模型，简记为 $ARCH(q)$

---

$ARCH$ 模型的作用

我们知道构造 $ARCH$ 模型的目的是使用自回归的方法提取误差平方序列中蕴涵的相关信息.那么构造出这个模型有什么用？和之前学的模型之间有什么关系？

比如，在上篇我们队 1952 - 1988 年中国农业国民收入指数序列建模，得到的拟合模型为:

$$x_t = x_{t-1} + \epsilon_t + 0.7355 \epsilon_{t-1}, Var(\epsilon_t) = 61.95$$
根据这个模型，我们只要知道过去一年的历史观察值 $x_{t-1}$和过去一年的估计误差 $\epsilon_{t-1}$，就能估计今年的平均水平 $\hat{x}_t$

这个序列我们也可以同残差自回归模型或者确定性因素分解模型来估计，它们得到的最终模型结构和结果可能会不一样，但是它们做的工作性质是相同的，都是对该序列水平的拟合.

水平只是一个点估计，无法给出估计精度，所以通常还需要估计出其置信区间.之前求置信区间时，都假定残差序列方差齐性.这意味着，无论过去的真实波动情况如何，在该例子中，残差序列的方差 $Var(\epsilon_t) = 61.95$

这种假定在异方差场合就会出现问题，不妨假定该序列残差具有集群效应，如果考察过去的残差波动情况发现，近期正处于大起大落的时期，那么残差的真实方差通常就比 $Var(\epsilon_t)$大，这时按照方差齐性的假定估计的 $95\%$的置信区间，它的真实置信水平一定低于 $95\%$ .这就给投资人带来了不可评估的投资风险.

而 $ARCH$ 模型就是要构造一个模型，利用历史信息，得到条件方差信息

$$Var(\epsilon_t | \epsilon_{t-1},\epsilon_{t-2},\cdots) = E(\epsilon_t^2 | \epsilon_{t-1},\epsilon_{t-2},\cdots) \\= \omega + \sum_{j=1}^q \lambda_j \epsilon_{t-j}^2$$
$ARCH$模型的实质是将历史波动信息作为条件，并采用某种自回归形式来刻画波动的变化.对于一个时间序列而言，在不同的时刻包含的历史信息不同，因而相应的条件方差也不同.利用 $ARCH$ 模型，可以刻画出随时间变化而变化的条件方差，它比无条件方差更及时地反映了序列几期波动的特征，这就是 $ARCH$ 模型的作用.它和前面介绍的 $ARIMA$ 模型、残差自回归模型、确定性因素分解模型是两种性质的模型，它关注的是序列的波动性拟合.

---

拿到一个观察值序列后，完整的分析应该关注水平和波动两方面.我们通常会首先提取序列的水平相关信息，然后分析方差序列中蕴涵的波动相关信息.将这两方面的信息综合起来才是比较完整和精确的分析结果.

所以使用 $ARCH$ 模型提取异方差中蕴涵的相关信息的完整结构为:

$$\begin{cases} x_t = f(t,x_{t-1},x_{t-2},\cdots) + \epsilon_t \\ \epsilon_t = \sqrt{h_t} e_t \\ h_t = \omega + \sum_{j=1}^q \lambda_j \epsilon_{t-j}^2 \end{cases}$$ 式中，$f(t,x_{t-1},x_{t-2},\cdots)$ 为 $\{ x_t \}$ 的确定性信息拟合模型，$e_t \approx N(0,\sigma^2)$

---

$ARCH$ 检验

要拟合 $ARCH$ 模型，首先需要进行 $ARCH$ 检验.$ARCH$检验是一种特殊的异方差检验，它不仅要求序列具有异方差性，而且要求这种异方差性是由某种自相关关系造成的，这种自相关关系可以用残差序列的自回归模型进行拟合.常用的两种 $ARCH$ 检验统计方法是$Portmanteau Q$检验和 $LM$ 检验.

$Portmanteau Q$检验

1983 年 Mcleod 和 Li 提出了 Portmanteau Q 统计方法，用于检验残差平方序列的自相关性，现在它是 ARCH 检验统计方法之一.

该检验方法的构造思想是：如果残差序列方差非齐，且具有集群效应，那么残差平方序列通常具有相关性，所以方差非齐检验可以转化为残差平方序列的自相关性jian'y检验.

Portmanteau Q 检验的假设条件为:

$$H_0 : 残差平方序列纯随机 \ \ \ \ (方差齐性) \\ H_1 : 残差平方序列自相关 \ \ \ \ (方差非齐)$$
用 $\rho_k$ 表示残差序列平方序列 $\{ \epsilon_t^2 \}$ 的延迟 $k$阶自相关系数，则该假设条件可以等价表达为: $$H_0 : \rho_1 = \rho_2 = \cdots = \rho_q = 0 \\ H_1 : \rho_1,\rho_2,\cdots,\rho_q 不全为零$$
Portmanteau Q 检验统计量实际上就是 $\epsilon_t^2$ 的 $LB$ 统计量: $$Q(q) = n (n+2) \sum_{i=1}^q \frac{\rho_i^2}{n-i}$$ 式中，$n$为观察序列长度；$\rho_i$ 为残差序列延迟 $i$阶自相关系数，有 $$\rho_i = \sqrt{\frac{\sum_{t = i+1}^n (\epsilon_t^2 - \hat{\sigma}^2)(\epsilon_{t-i}^2 - \hat{\sigma}^2)}{\sum_{t=1}^n{(\epsilon_t^2 - \hat{\sigma}^2)^2}}} , \hat{\sigma}^2 = \frac{\sum_{t=1}^n{\epsilon_t^2}}{n}$$

原假设成立时，Portmanteau Q 统计量近似服从自由度为 $q - 1$ 的 $\chi^2$ 分布:

$$Q(q) \approx \chi^2(q - 1)$$ 当 $Q(q)$ 检验统计量的 $P$ 值小于显著性水平 $\alpha$ 时，拒绝原假设，认为该序列方差非齐且具有自相关关系.

---

拉格朗日乘子检验

1982 年 Engle 提出了一种重要的 $ARCH$ 检验方法: 拉格朗日乘子检验(Lagrange multiplier test)，简记为 $LM$ 检验.

拉格朗日乘子检验的构造思想是: 如果残差序列方差非齐，且具有集群效应，那么残差平方序列通常具有自相关性. 我们可以尝试使用自回归模型(ARCH(q)模型)拟合残差平方序列

$$\epsilon_t^2 = \omega + \sum_{j=1}^q \lambda_j \epsilon_{t-j}^2 + e_t$$ 于是方差齐性检验就可以转化为这个方程是否显著成立的检验.

如果方程显著成立(至少存在一个参数 $\lambda_j$ 非零)，那就意味着残差平方序列具有自相关性，可以用该回归方程提取自相关信息.

反之，如果方程不能显著成立($\lambda_j = 0;j = 1,2,\cdots,q$)，就意味着残差平方序列不存在显著的自相关性，不能拒绝方差齐性假定.所以拉格朗日乘子检验实际上是残差平方序列 $\epsilon_t^2$ 自回归方程的显著性检验.

---

拉格朗日乘子检验的假设条件为:

$$H_0 : 残差平方序列纯随机 \\ H_1 : 残差平方序列具有自相关性$$ 对残差平方序列构造$q$ 阶自回归方程，假设条件等价于: $$H_0 : \lambda_1 = \lambda_2 = \cdots =\lambda_q = 0 \\ H_1 : \lambda_1,\lambda_2,\cdots , \lambda_q 不全为零$$ 记总误差平方和为 $SST = \sum_{t = q + 1}^T \epsilon_t^2$，自由度为 $T - q - 1$ .回归平方和为 $SSR = SST - SSE$，自由度为 $q$，其中，$SSE$方程残差平方和，$SSE = \sum_{t = q+1}^T e_t^2$，自由度为 $T - 2q - 1$.则 $LM$ 检验统计量为: $$LM(q) = \frac{(SST-SSE)/q}{SSE/(T-2q -1)}$$ 原假设成立时，$LM(q)$统计量jin's近似服从自由度$q - 1$的 $\chi^2$ 分布 $$LM(q) \approx \chi^2(q - 1)$$
当 $LM(q)$ 检验统计量的 $P$值小于显著水平 $\alpha$时，拒绝原假设，认为该序列方差非齐，并且可以用 $q$ 阶自回归模型拟合残差平方序列中的自相关系数.

---

在 R语言中，做拉格朗日乘子检验可以使用 FinTS程序包，这个包中有个 ArchTest函数专门作 $LM检验$.而 Portmanteau Q 检验其实就是对残差平方序列进行纯随机性检验.所以对残差序列进行平方yu运算后，只有调用 Box.test()函数就可以完成 Portmanteau Q 检验.

拟合 $ARCH$ 模型可以调用 tseries包中的 garch函数.grach函数的命令g格式为: garch(x, order = (p,q))，式中 x表示序列名，order表示拟合模型阶数，详情可使用help(garch)来查看.

下面还是对标准普尔 500 股票价值加权月度收益率序列进行 $ARCH$检验，并拟合该序列的波动特征:

# Portmanteau Q 检验
> for(i in 1:5) print(Box.test(x^2,lag = i))
    Box-Pierce test
data:  x^2
X-squared = 55.545, df = 1, p-value = 9.137e-14
    Box-Pierce test
data:  x^2
X-squared = 85.09, df = 2, p-value < 2.2e-16
    Box-Pierce test
data:  x^2
X-squared = 126.06, df = 3, p-value < 2.2e-16
    Box-Pierce test
data:  x^2
X-squared = 138.74, df = 4, p-value < 2.2e-16
    Box-Pierce test
data:  x^2
X-squared = 141.9, df = 5, p-value < 2.2e-16
>
# 加载 garch函数的包
> library(tseries)
    ‘tseries’ version: 0.10-42
    ‘tseries’ is a package for time series analysis and
    computational finance.
    See ‘library(help="tseries")’ for details.
# ARCH(3)模型拟合
> x.fit <- garch(x,order = c(0,3))
 ***** ESTIMATION WITH ANALYTICAL GRADIENT ***** 
     I     INITIAL X(I)        D(I)
     1     2.904816e-03     1.000e+00
     2     5.000000e-02     1.000e+00
     3     5.000000e-02     1.000e+00
     4     5.000000e-02     1.000e+00
    IT   NF      F         RELDF    PRELDF    RELDX   STPPAR   D*STEP   NPRELDF
     0    1 -1.904e+03
     1    5 -1.909e+03  2.72e-03  1.20e-02  1.0e-02  2.3e+07  1.0e-03  1.37e+05
     2    6 -1.912e+03  1.68e-03  3.42e-03  6.4e-03  2.0e+00  1.0e-03  4.09e+01
     3    7 -1.913e+03  6.03e-04  5.11e-04  7.3e-03  2.0e+00  1.0e-03  4.33e+01
     4   11 -1.930e+03  8.56e-03  1.17e-02  2.9e-01  2.0e+00  5.6e-02  4.25e+01
     5   15 -1.930e+03  3.11e-05  2.99e-04  7.0e-04  7.7e+00  1.3e-04  2.58e-01
     6   16 -1.930e+03  5.76e-05  5.35e-05  5.3e-04  2.0e+00  1.3e-04  2.42e-01
     7   21 -1.930e+03  1.81e-04  2.69e-04  7.6e-02  2.0e+00  1.6e-02  2.40e-01
     8   23 -1.930e+03  7.75e-06  1.49e-04  4.7e-02  2.0e+00  1.2e-02  2.13e-02
     9   24 -1.931e+03  2.01e-04  2.22e-04  2.1e-02  2.0e+00  6.0e-03  3.53e-02
    10   25 -1.931e+03  8.77e-05  1.22e-04  2.2e-02  2.0e+00  6.0e-03  1.15e-01
    11   26 -1.931e+03  1.78e-04  2.33e-04  2.4e-02  2.0e+00  6.0e-03  2.20e-02
    12   29 -1.935e+03  1.75e-03  3.45e-03  2.1e-01  1.8e+00  5.9e-02  4.92e-02
    13   30 -1.942e+03  3.85e-03  5.60e-03  1.8e-01  1.2e+00  5.9e-02  1.54e-02
    14   31 -1.945e+03  1.61e-03  1.22e-03  1.2e-01  1.9e-02  5.9e-02  1.22e-03
    15   32 -1.946e+03  6.13e-04  4.70e-04  9.4e-02  0.0e+00  5.1e-02  4.70e-04
    16   33 -1.947e+03  1.02e-04  8.61e-05  4.3e-02  0.0e+00  2.7e-02  8.61e-05
    17   34 -1.947e+03  5.54e-06  4.97e-06  1.2e-02  0.0e+00  7.4e-03  4.97e-06
    18   35 -1.947e+03  3.35e-07  2.31e-07  2.5e-03  0.0e+00  1.4e-03  2.31e-07
    19   36 -1.947e+03  2.25e-07  1.75e-07  2.2e-03  0.0e+00  1.4e-03  1.75e-07
    20   37 -1.947e+03  6.16e-08  4.86e-08  1.0e-03  0.0e+00  6.4e-04  4.86e-08
    21   38 -1.947e+03  1.16e-08  9.94e-09  4.5e-04  0.0e+00  2.5e-04  9.94e-09
    22   39 -1.947e+03  8.74e-10  7.68e-10  8.2e-05  0.0e+00  6.2e-05  7.68e-10
    23   40 -1.947e+03  3.90e-11  3.57e-11  2.0e-05  0.0e+00  1.3e-05  3.57e-11
 ***** RELATIVE FUNCTION CONVERGENCE *****
 FUNCTION    -1.946628e+03   RELDX        2.006e-05
 FUNC. EVALS      40         GRAD. EVALS      24
 PRELDF       3.567e-11      NPRELDF      3.567e-11
     I      FINAL X(I)        D(I)          G(I)
     1    1.436507e-03     1.000e+00    -1.670e-01
     2    7.953834e-02     1.000e+00     8.530e-04
     3    2.231052e-01     1.000e+00    -7.066e-04
     4    2.732265e-01     1.000e+00    -5.770e-04
# 查看拟合结果
> summary(x.fit)
Call:
garch(x = x, order = c(0, 3))
Model:
GARCH(0,3)
Residuals:
    Min      1Q  Median      3Q     Max 
-6.2420 -0.3985  0.1671  0.7501  4.4193 
Coefficient(s):
    Estimate  Std. Error  t value Pr(>|t|)    
a0 1.437e-03   6.903e-05   20.809  < 2e-16 ***
a1 7.954e-02   2.821e-02    2.820   0.0048 ** 
a2 2.231e-01   2.587e-02    8.624  < 2e-16 ***
a3 2.732e-01   4.384e-02    6.232 4.61e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagnostic Tests:
    Jarque Bera Test
data:  Residuals
X-squared = 585.27, df = 2, p-value < 2.2e-16
    Box-Ljung test
data:  Squared.Residuals
X-squared = 8.8831e-06, df = 1, p-value = 0.9976
>
# arch(3)模型预测
> x.pred <- predict(x.fit)
#画出预测结果图
> plot(x.pred)
>

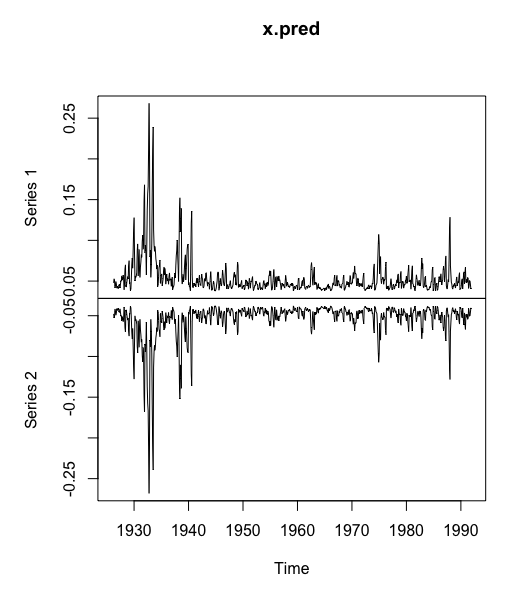
> plot(x)
> lines(x.pred[,1],col = 2)
> lines(x.pred[,2],col = 2)
> abline(h = 1.96*sd(x),col = 4, lty = 2)
> abline(h=-1.96*sd(x),col = 4, lty = 2)
>

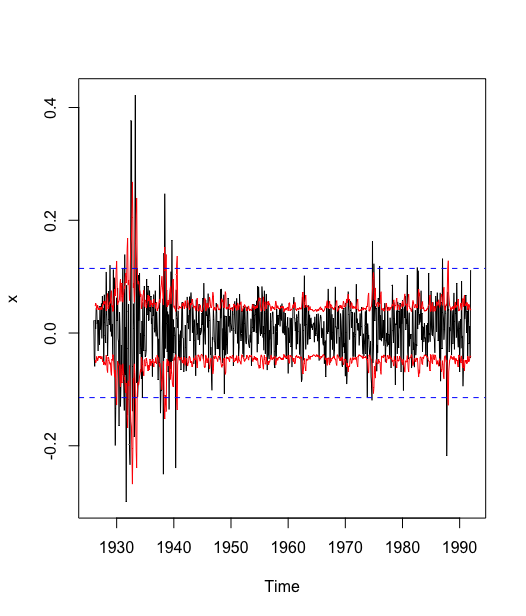
$LM$ 检验和 $Q$检验都显示该序列显著方差非齐，且残差平方序列具有显著自相关关系，可以用 $ARCH$ 模型提取残差平方序列中蕴涵的相关信息. 而 $LM$检验和 $Q$检验都显示 1 阶至 5阶 $ARCH$模型均显著成立，这说明残差平方序列具有长期相关，$ARCH(q)$ 模型的阶数 q 将会比较大. 本例尝试拟合过 $ARCH(5)$ 和 $ARCH(4)$ ，这两个模型的参数检验结果均显示有参数不显著，直至 $ARCH(3)$ 模型，检验结果显示模型显著，参数均显著.所以最后得到的拟合模型是 $ARCH(3)$ 模型:

$$E( \epsilon_t^2 | \epsilon_{t-1},\epsilon_{t-2},\cdots) = 0.001437 + 0.07954 \epsilon_{t-1}^2 + 0.2231 \epsilon_{t-2}^2 + 0.2732 \epsilon_{t-3}^2$$ 从拟合图中可以看出，条件异方差模型对序列波动的预测将会更加准确.

---

$GARCH$ 模型

$GARCH$ 模型的定义

$ARCH$ 模型的实质是使用残差平方序列的 $q$ 阶移动平均拟合当期异方差函数值.由于移动平均模型具有自相关系数 $q$ 阶截尾性，所以 $ARCH$ 模型实际上只适用于异方差函数短期自相关过程.

但在实践中，有些残差序列的异方差函数是具有长期自相关性的，这时如果使用 $ARCH$ 模型拟合异方差函数，将会产生很高的移动平均阶数，增加参数估计的难度并最终影响 $ARCH$ 模型的拟合精度.

为了修正这个问题，Bollerslov 在 1985 年提出了广义自回归条件异方差(generalized autoregressive conditional heteroskedastic) 模型，它的结构如下:

$$\begin{cases} x_t = f(t,x_{t-1},x_{t-2},\cdots) + \epsilon_t \\ \epsilon_t = \sqrt{h_t} e_t \\ h_t = \omega + \sum_{i = 1}^p \eta_i h_{t - i} + \sum_{j = 1}^q \lambda_j \epsilon_{t-j}^2 \end{cases}$$ 式中，$f(t,x_{t-1},x_{t-2},\cdots)$为 $\{ x_t \}$ 的确定性信息拟合模型；$e_t \approx N(0,\sigma^2)$ .这个模型简记为 GARCH(p,q).

GARCH 模型实际上就是在 ARCH 模型的基础上，增加考虑了异方差函数的 p 阶自相关性而形成的；它可以有效地拟合具有长期记忆性的异方差函数.显然 $$ARCH$ 模型是 $GARCH$模型的一个特例，$ARCH(q)$ 模型实际上就是 $p = 0$的 $GARCH(p,q)$ 模型.

---

$AR-GARCH$ 模型

对序列 $\{ \epsilon_t \}$ 拟合 $GARCH$模型有一个基本要求: $\{ \epsilon_t \}$ 为零均值、纯随机、异方差序列.有时回归函数 $f(t,x_{t-1},x_{t-2},\cdots)$ 不能充分提取原序列中的相关信息，$\{ \epsilon_t \}$ 可能具有自相关性，而不是纯随机的.这时需要先对 $\{ \epsilon_t \}$ 拟合自回归模型，在考察自回归残差序列 $\{ v_t \}$ 的方差齐性，如果 $\{ v_t \}$ 异方差，对它拟合 $GARCH$模型.这样构造的模型称为 $AR(m)-GARCH(p,q)$模型

$$\begin{cases} x_t = f(t,x_{t-1},x_{t-2},\cdots) + \epsilon_t \\ \epsilon_t = \sum_{k=1}^m \beta_k \epsilon_{t-k} + v_t \\ v_t = \sqrt{h_t} e_t \\ h_t = \omega + \sum_{i=1}^p \eta_i h_{t-i} + \sum_{j=1}^q \lambda_j v_{t-j}^2 \end{cases}$$ 式中，$f(t,x_{t-1},x_{t-2},\cdots)$ 为 $\{ x_t \}$ 的确定性xin'x；$e_t \approx N(0,1)$.

---

下面分析拟合 1979 年 12月 31日 至 1991 年 12月 31日 外币对美元的日兑换率序列:

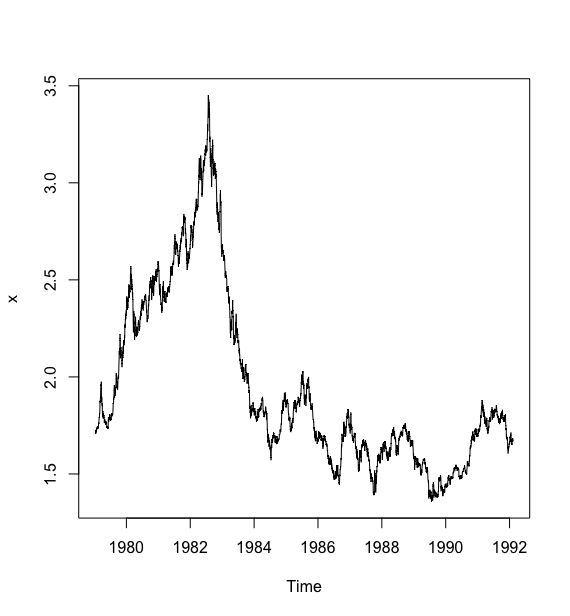
#读取数据
> w <- read.table("data/file23.csv",sep = ",",header = T)
> x <- ts(w$exchange_rates,start = c(1979,12,31),frequency = 365)
> plot(x)
> 

# 绘制差分序列的时序图
> plot(diff(x))
> 

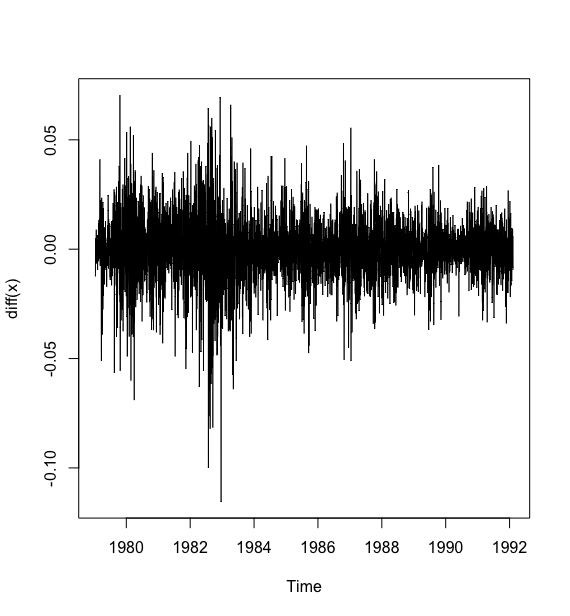
# 考察差分序列的相关系数
> acf(diff(x))
>

xia# 考察差分序列的偏相关系数
> pacf(diff(x))
>

# 差分序列的白噪声检验
> for(i in 1:2) print(Box.test(diff(x),lag = 6*i))
    Box-Pierce test
data:  diff(x)
X-squared = 12.917, df = 6, p-value = 0.04438
    Box-Pierce test
data:  diff(x)
X-squared = 29.712, df = 12, p-value = 0.003085
>

可以看到差分序列的白噪声检验并不显著，所以原序列存在异方差性.

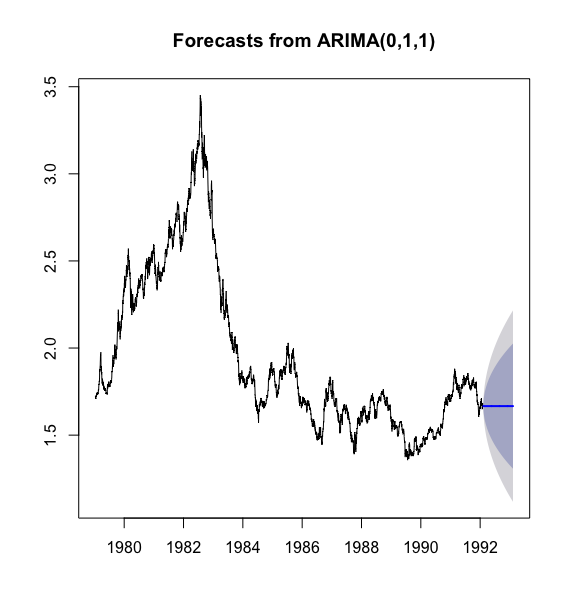
# 使用 arima(0,1,1) 模型提取水平相关信息
> x.fit <- arima(x,order = c(0,1,1))
> x.fit
Call:
arima(x = x, order = c(0, 1, 1))
Coefficients:
         ma1
      0.0357
s.e.  0.0143
sigma^2 estimated as 0.0002007:  log likelihood = 13545.61,  aic = -27087.22
> 
# 对拟合后的残差序列进行白噪声检验
> for(i in 1:6) print(Box.test(x.fit$residual,type = "Ljung-Box",lag = i))
    Box-Ljung test
data:  x.fit$residual
X-squared = 0.0005354, df = 1, p-value = 0.9815
    Box-Ljung test
data:  x.fit$residual
X-squared = 0.55102, df = 2, p-value = 0.7592
    Box-Ljung test
data:  x.fit$residual
X-squared = 2.6528, df = 3, p-value = 0.4483
    Box-Ljung test
data:  x.fit$residual
X-squared = 3.3062, df = 4, p-value = 0.5079
    Box-Ljung test
data:  x.fit$residual
X-squared = 6.8276, df = 5, p-value = 0.2338
    Box-Ljung test
data:  x.fit$residual
X-squared = 6.8306, df = 6, p-value = 0.3368
>
# 导入预测必要的包
> library(forecast)
# 水平信息的预测
> x.fore <- forecast(x.fit,h = 365)
> plot(x.fore)
> 

# Pormanteau Q 检测
> for(i in 1:6) print(Box.test(x.fit$residuals^2,type = "Ljung-Box",lag = i))
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 82.803, df = 1, p-value < 2.2e-16
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 237.9, df = 2, p-value < 2.2e-16
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 343.33, df = 3, p-value < 2.2e-16
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 490.84, df = 4, p-value < 2.2e-16
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 602.1, df = 5, p-value < 2.2e-16
    Box-Ljung test
data:  x.fit$residuals^2
X-squared = 841.96, df = 6, p-value < 2.2e-16
>

# garch(1,1) 模型提取波动信息
> library(tseries)
> r.fit <- garch(x.fit$residuals,order = c(1,1))
 ***** ESTIMATION WITH ANALYTICAL GRADIENT ***** 
     I     INITIAL X(I)        D(I)
     1     1.806109e-04     1.000e+00
     2     5.000000e-02     1.000e+00
     3     5.000000e-02     1.000e+00
    IT   NF      F         RELDF    PRELDF    RELDX   STPPAR   D*STEP   NPRELDF
     0    1 -1.800e+04
     1    7 -1.800e+04  1.28e-04  3.05e-04  1.0e-04  5.5e+10  1.0e-05  8.36e+06
     2    8 -1.800e+04  5.34e-06  5.87e-06  9.8e-05  2.0e+00  1.0e-05  2.84e+01
     3   16 -1.807e+04  3.63e-03  6.18e-03  5.2e-01  2.0e+00  1.1e-01  2.83e+01
     4   18 -1.819e+04  6.73e-03  9.78e-03  7.7e-01  2.0e+00  4.4e-01  5.00e+00
     5   22 -1.819e+04  1.22e-04  1.77e-02  1.9e-02  2.0e+00  2.0e-02  5.70e-01
     6   26 -1.831e+04  6.22e-03  2.96e-03  1.3e-01  1.7e+00  1.6e-01  1.42e-02
     7   32 -1.833e+04  1.49e-03  1.58e-03  2.4e-06  4.5e+01  3.2e-06  2.29e-01
     8   33 -1.837e+04  2.05e-03  2.29e-03  4.8e-06  4.0e+00  6.3e-06  2.84e+00
     9   34 -1.837e+04  1.06e-04  4.42e-04  3.6e-06  2.0e+00  6.3e-06  4.46e-01
    10   35 -1.838e+04  1.63e-04  2.09e-04  4.3e-06  2.0e+00  6.3e-06  9.74e-02
    11   36 -1.838e+04  5.21e-06  4.66e-06  4.6e-06  2.0e+00  6.3e-06  1.36e-01
    12   37 -1.838e+04  1.48e-07  1.63e-07  4.6e-06  2.0e+00  6.3e-06  1.42e-01
    13   44 -1.838e+04  1.48e-04  2.91e-04  1.9e-02  2.0e+00  2.6e-02  1.42e-01
    14   46 -1.842e+04  2.33e-03  1.15e-03  4.6e-02  0.0e+00  8.6e-02  1.15e-03
    15   48 -1.844e+04  9.88e-04  9.84e-04  1.8e-02  1.8e+00  3.4e-02  1.46e-02
    16   50 -1.848e+04  1.89e-03  1.90e-03  3.4e-02  1.5e+00  6.9e-02  3.78e-02
    17   51 -1.849e+04  8.65e-04  3.36e-03  5.8e-02  1.6e+00  1.4e-01  2.18e-02
    18   53 -1.850e+04  2.20e-04  5.04e-03  4.1e-03  1.5e+00  9.4e-03  5.09e-03
    19   56 -1.851e+04  9.04e-04  7.21e-04  5.0e-03  1.5e+00  1.1e-02  1.25e-03
    20   57 -1.852e+04  5.17e-04  8.81e-04  5.9e-03  1.5e+00  1.1e-02  1.70e-03
    21   58 -1.852e+04  1.15e-04  1.24e-04  4.7e-03  0.0e+00  1.0e-02  1.24e-04
    22   59 -1.853e+04  3.66e-05  3.82e-05  4.4e-03  3.9e-01  1.0e-02  4.13e-05
    23   61 -1.853e+04  1.72e-06  2.65e-06  2.1e-04  1.5e+00  4.8e-04  1.16e-05
    24   71 -1.853e+04  2.00e-07  4.83e-07  1.2e-08  3.5e+00  2.3e-08  1.82e-06
    25   81 -1.853e+04  4.30e-07  5.19e-07  3.9e-04  6.4e-01  8.9e-04  6.97e-07
    26   82 -1.853e+04  5.83e-08  9.89e-08  2.6e-04  0.0e+00  5.8e-04  9.89e-08
    27   83 -1.853e+04  8.04e-10  3.34e-11  3.5e-06  0.0e+00  7.1e-06  3.34e-11
    28   84 -1.853e+04 -9.81e-12  1.56e-14  4.2e-08  0.0e+00  7.7e-08  1.56e-14
 ***** RELATIVE FUNCTION CONVERGENCE *****
 FUNCTION    -1.852505e+04   RELDX        4.199e-08
 FUNC. EVALS      84         GRAD. EVALS      28
 PRELDF       1.558e-14      NPRELDF      1.558e-14
     I      FINAL X(I)        D(I)          G(I)
     1    2.133129e-06     1.000e+00    -1.886e+00
     2    7.623127e-02     1.000e+00    -8.062e-03
     3    9.143603e-01     1.000e+00    -6.761e-03
> summary(r.fit)
Call:
garch(x = x.fit$residuals, order = c(1, 1))
Model:
GARCH(1,1)
Residuals:
     Min       1Q   Median       3Q      Max 
-4.83074 -0.58407  0.02616  0.58758  4.54060 
Coefficient(s):
    Estimate  Std. Error  t value Pr(>|t|)    
a0 2.133e-06   3.014e-07    7.077 1.48e-12 ***
a1 7.623e-02   5.456e-03   13.972  < 2e-16 ***
b1 9.144e-01   6.015e-03  152.009  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagnostic Tests:
    Jarque Bera Test
data:  Residuals
X-squared = 319.23, df = 2, p-value < 2.2e-16
    Box-Ljung test
data:  Squared.Residuals
X-squared = 0.28019, df = 1, p-value = 0.5966
>
# 预测波动信息，绘制波动置信区间
> r.pred <- predict(r.fit)
> plot(r.pred)
> 

从原始数据的时序图可以看出，序列非平稳，有明显的趋势特征.差分后序列时序图显示趋势消除，但是有明显的集群效应.所以分析该序列需要同时提取水平相关信息和波动相关信息.

水平信息的提取时考察差分后序列的自相关图和偏自相关图，拟合 $ARIMA(0,1,1)$模型，该拟合模型的残差白噪声检测显示该模型显著成立.利用该拟合模型，还可以预测序列未来的水平.

波动信息的提取首先是考虑 $ARIMA(0,1,1)$ 模型的残差平方序列的异方差特征. Portmanteau Q 检验显示残差序列显著方差非齐，且具有长期相关性.所以构造 $GARCH(1,1)$ 模型，并根据该模型的拟合结果绘制波动的 95% 置信区间图.

综合水平模型和波动模型，我们得到的完整拟合模型为:

$$\begin{cases} \nabla x_t = \epsilon_t + 0.0357 \epsilon_{t-1} + v_t, v_t \approx N(0,0002) \\ v_t = \sqrt{h_t} e_t \\ h_t = 0.9144 h_{t-1} + 0.071623 v_{t-1}^2 \end{cases}$$