机器学习篇

AdaBoost提升

AdaBoost提升是基于 Boosting算法的一种集成学习算法，本篇会详细讲解Boosting算法的思路，以及AdaBoost具体操作流程和推导过程，最后会用R代码演示如何使用 AdaBoost算法.

集成学习

我们之前讲的随机森林也是一种集成学习，这里正式介绍下什么是集成学习.

我们分类中用到很多经典的分类算法，比如 SVM、logistic 等等，要训练单个分类器达到很高的精度比较困难，我们很自然想到的一个方法就是能否整合多个算法优势到解决某一个特定分类问题中去，而每一个单独的分类器不需要特别高的分类精度，答案是肯定的，这就是集成学习的思路.

通过聚合多个分类器的预测来提高分类的准确率，这种技术称为集成学习(ensemble learning)。集成学习由训练数据构建一组不同的基分类器，然后通过对每个基分类器的预测进行权重控制来进行投票分类.

假设考虑 25 个二元分类问题，每个分类器的分类误差为0.35，如果所有基分类器都是相互独立的（即误差是不相关的），则在超过一半的基分类器预测错误的组合情况下，才认为整个分类器预测错误，这种情况下的组合分类器的误差率为:

$$e_{ensemble} = \sum_{i = 13}^{25} C_{25}^i \epsilon^i (1 - \epsilon)^{25-i} = 0.06$$ 下图对角线表示所有基分类器都是等同的情况，实线是基分类器独立时的情况:

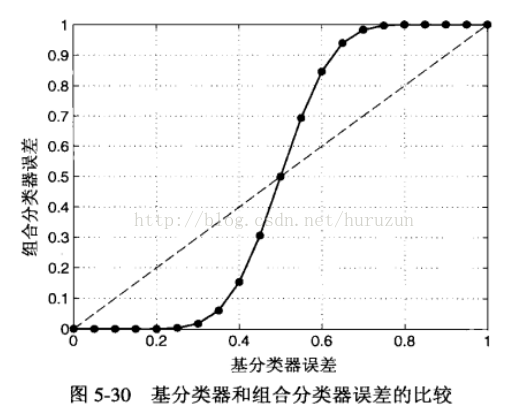
组合分类器性能优于单个分类器必须满足两个条件:

• 基分类器之间是相互独立的.
• 基分类器应当优于随机猜测分类器.

实践中很难保证基分类器之间完全独立，但是在基分类器轻微相关的情况下，集成学习依然可以提高分类的准确率.

集成学习一般有两类:

1. 平均方法(averaging methods)
   它的原理是分别建立多个独立的评计量，然后通过投票预测；一般来说，总估计量通常比单一的估计量要好，因为它的方差减少了.

   这类算法的代表是: Bagging 方法，随机森林 等等.

2. 提升方法(boosting methods)
   它的原理是将几个弱模型结合起来，形成一个强大的整体，其中基本的估计量是按顺序建立的，并试图减少组合估计量的偏差.

   代表算法有: AdaBoost，梯度提升树(GBDT)

在前面的篇章中我们已经讲解过 随机森林 的原理了，下面我们会依次讲解 AdaBoost提升算法 和 GBDT 梯度提升树的算法原理.

---

AdaBoost 算法

强可学习与弱可学习

强可学习是指一个学习算法能很好的对训练集进行学习并且有很高的正确率.

弱可学习要求没强可学习那么高，只需要学习的正确率仅比随机猜测要好即可.

所以弱可学习相比于强可学习来说更容易获得，但在实践中人们往往希望用更少的基学习器来进行学习，所以往往使用强可学习的学习器来作为基学习器.

---

提升方法有两个问题:

1. 每一轮如何改变训练数据的权重或概率分布.

2. 如何将弱分类器整合为强分类器.

很朴素的思想解决这两个问题:

1. 提高被前一轮弱分类器错误分类的权值，而降低那些被正确分类的样本的权值，这就使得那些没有得到正确分类的样本，由于权值加重，所以会受到下一轮弱分类器的更大关注.

2. Adaboost采用加权多数表决的方法，即加大分类误差率小的弱分类器的权值，使其在表决中起到较大的作用，相反减小误差率大的弱分类器的权值，使其在表决中起到较小的作用.

注意这里的基学习器并没有规定一定要是决策树或是SVM等，泛指所有的分类器；

这就说明 Boosting 方法更多的是一种思路，或者说是框架，可以与多种分类算法相结合.

---

AdaBoost过程

输入: 训练集 $D = \{ (x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m) \}$;
$\qquad$ 基学习算法 $\cal{L}$;
$\qquad$ 训练轮数 $T$.
过程:

1. $D_1(x) = \frac{1}{m}$
2. $for \quad t = 1,2,\cdots,T \quad do$
3. $\qquad h_t = \cal{L}(D,D_t)$;
4. $\qquad \epsilon_t = P_{x-D_t} (h_t(x) \neq f(x))$;
5. $\qquad if \quad \epsilon_t > 0.5 \quad then \ break$;
6. $\qquad \alpha_t = \frac{1}{2} \ln{\left( \frac{1 - \epsilon_t}{\epsilon_t} \right)}$;
7. $\qquad \begin{array} & D_{t+1}(x) &=& \frac{D_t(x)}{Z_t} \times \begin{cases} \exp(-\alpha_t), & if \ h_t(x) = f(x) \\ \exp(\alpha_t),& if \ h_t(x) \neq f(x) \end{cases} \\ &=& \frac{D_t(x) \exp(-\alpha_t f(x) h_t(x))}{Z_t} \end{array}$
8. $end \ for$

输出: $H(x) = sign \left( \sum_{t=1}^T \alpha_t h_t(x) \right)$

---

这里对上述算法过程进行说明:

首先有训练集 $D$，且给每个样本的初始权重为 $\frac{1}{m}$，然后开始迭代提升，逐步改变分类错误样本的权重.

对每一次迭代来说，第一步就是在 $D_t(x)$ 数据集上训练一个分类器 $h_t$，也就是算法中的(3)步；该分类器可以是决策树、SVM或logistic等等；$D_t(x)$ 是第 $t$ 步时的训练集分布，与初始训练集的不同就是每个样本的权重进行了重新分配.

(4)步是计算新训练的分类器的误差率.

(5)步是判断 $t$ 次迭代训练的分类器是否比随机猜测更好，如果得到的分类器比随机猜测坏的话就直接退出训练.

(6)(7)步是根据当前分类器的分类误差来更新每个样本的权重，以便下一轮弱分类器的训练；其中 $f(x),h_t(x) \in \{ -1,+1 \}$.

最后输出这一步是加权多数表决的过程，$sign()$ 是符号函数，即

$$sign(z) = \begin{cases} 1, & z > 0 \\ 0, & z = 0 \\ -1, & z < 0 \end{cases}$$

---

AdaBoost推导过程

前面我们将了算法过程，其中涉及到几个公式，既然是学习，我们就需要知其然知其所以然。

AdaBoost算法有多种推导方式，其中比较容易理解的是基于“加性模型”(additive model)，即基学习器的线性组合:

$$H(x) = \sum_{t=1}^T \alpha_t h_t(x)$$ 来最小化指数损失函数: $$l_{exp}(H|D) = E_{x \approx D} \left[ e^{-f(x) H(x)} \right]$$
若 $H(x)$ 能令指数损失函数最小化，则考虑损失函数对 $H(x)$ 的偏导为零: $$\begin{array} & \frac{\partial l_{exp}(H|D) }{\partial H(x)} &=& E_{x \approx D} \left[ e^{-f(x) H(x)} * (- f(x)) \right] \\ &=& -e^{-H(x)} P(f(x) = 1 | x) + e^{H(x)} P(f(x)=-1 | x) \\ &=& 0 \end{array}$$ 可解得 $$H(x) = \frac{1}{2} \ln{\frac{P(f(x) = 1 | x)}{P(f(x) = -1 | x)}}$$
因此有 $$\begin{array} & sign(H(x)) &=& sign \left( \frac{1}{2} \ln{\frac{P(f(x) = 1 | x)}{P(f(x) = -1 | x)}} \right) \\ &=& \begin{cases} 1, & P(f(x) = 1 | x) > P(f(x) = -1 |x) \\ -1, & P(f(x) = 1 | x) < P(f(x) = -1 |x) \end{cases} \\ &=& \arg \max_{y \in \{-1,1\}} P(f(x) = y |x) \end{array}$$
这意味着若指数损失函数最小化，则分类错误率也将最小化；这说明指数损失函数是分类任务原 $0/1$ 损失函数的一致的替代损失函数.因为指数损失函数数学性质更好.

---

上面一步说明了指数损失函数是有效的.下面考虑当基分类器 $h_t$ 基于分布 $D_t$ 产生后，该基分类器的权重 $\alpha_t$ 应使得 $\alpha_t h_t$ 最小化指数损失函数:

$$\begin{array} & l_{exp}(\alpha_t h_t | D_t) &=& E_{x \approx D_t} \left[ e^{-f(x) \alpha_t h_t(x)} \right] \\ &=& E_{x \approx D_t} \left[ e^{-\alpha_t} I(f(x) = h_t(x)) + e^{\alpha_t} I(f(x) \neq h_t(x)) \right] \\ &=& e^{-\alpha_t} P_{x \approx D_t} (f(x) = h_t(x)) + e^{\alpha_t} P_{x \approx D_t} (f(x) \neq h_t(x)) \\ &=& e^{-\alpha_t}(1 - \epsilon_t) + e^{\alpha_t} \epsilon_t \end{array}$$ 其中 $\epsilon_t = P_{x \approx D_t}(h_t(x) \neq f(x))$ . 考虑指数损失函数的导数: $$\frac{\partial l_{exp}(\alpha_t h_t | D_t)}{\partial \alpha_t} = -e^{-\alpha_t}(1 - \epsilon_t) + e^{\alpha_t} \epsilon_t = 0$$ 解得: $$\alpha_t = \frac{1}{2} \ln{\left( \frac{1 - \epsilon_t}{\epsilon_t} \right)}$$ 这就是上面算法过程中第 (6) 步中的权值更新公式.

其中，$I(z) = \begin{cases} 1, & z = true; \\ 0, & z = false; \end{cases}$ 为示性函数.

---

AdaBoost算法在获得 $H_{t-1}$ 之后样本分布将进行调整，并学习下一轮基学习器 $h_t$，并且使得 $H_{t-1} + h_t$ 比 $H_{t-1}$ 的效果更好，即最小化

$$\begin{array} & l_{exp}(H_{t-1} + h_t | D) &=& E_{x \approx D} \left[ e^{-f(x) (H_{t-1}(x) + h_t(x))} \right] \\ &=& E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} e^{-f(x) h_t(x)} \right] \end{array}$$

单独考虑 $e^{-f(x) h_t(x)}$ :

$$\because e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!} \\ 又 \because f(x),h_t(x) \in \{ -1,+1 \} \\ \therefore e^{-f(x) h_t(x)} \approx 1 - f(x)h_t(x) + \frac{f^2(x) h_t^2(x)}{2} \\ = 1 - f(x)h_t(x) + \frac{1}{2}$$ 所以指数损失函数可以转换为: $$l_{exp} (H_{t-1} + h_t | D) \approx E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \left( 1 - f(x)h_t(x) + \frac{1}{2} \right) \right]$$

上述 $e^x$ 为泰勒展开式，对 $e^{-f(x) h_t(x)}$ 用了二阶泰勒展开.

于是理想的基学习器为:

$$\begin{array} & h_t(x) &=& arg \min_{h} l_{exp} (H_{t-1} + h_t | D) \\ &=& arg \min_{h} E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \left( 1 - f(x)h_t(x) + \frac{1}{2} \right) \right] \\ &=& arg \max_{h} E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} f(x)h_t(x) \right] \\ &=& arg \max_{h} E_{x \approx D} \left[ \frac{e^{-f(x) H_{t-1}(x)}}{E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \right]} f(x)h_t(x) \right] \end{array}$$ 需要注意的是，$E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \right]$ 是一个常数，已知的，因为在 $t$ 轮迭代时，前面的 $H_{t-1}(x)$ 已经知道了，其实 $e^{-f(x) H_{t-1}(x)}$ 也是已知的了.

于是令 $D_t$ 表示一个分布

$$D_t(x) = \frac{D(x) e^{-f(x) H_{t-1}(x)}}{E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \right]}$$
根据数学期望的定义，这等价于令 $$\begin{array} & h_t(x) &=& arg \max_{h} E_{x \approx D} \left[ \frac{e^{-f(x) H_{t-1}(x)}}{E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \right]} f(x)h_t(x) \right] \\ &=& arg \max_{h} E_{x \approx D_t} [f(x)h(x)] \end{array}$$
注意这里的数据集已经变了，由 $D$ 变成了 $D_t$，两者的差别是分布已由 $D_t(x)$ 的表达式更新了.

由于 $f(x),h(x) \in \{-1,1\}$，有

$$f(x)h(x) = 1 - 2*I(f(x) \neq f(x))$$ 则理想的基学习器为: $$h_t(x) = arg \min_{h} E_{x \approx D_t} [I(f(x) \neq h(x))]$$

由此可见，理想的 $h_t$ 将在分布 $D_t$ 下最小化分类误差.因此，弱分类器将基于分布 $D_t$ 来训练，且针对 $D_t$ 的分类误差应小于 0.5 . 这在一定程度上类似“残差逼近”的思想。

考虑到 $D_t$ 和 $D_{t+1}$ 的关系，有

$$\begin{array} & D_{t+1}(x) &=& \frac{D(x) e^{-f(x)H_t(x)}}{E_{x \approx D} \left[ e^{-f(x) H_t(x)} \right]} \\ &=& \frac{D(x) e^{-f(x) H_{t-1}(x)} e^{-f(x) \alpha_t h_t(x)}}{E_{x \approx D} \left[ e^{-f(x) H_t(x)} \right]} \\ &=& D_t(x) \cdot e^{ef(x) \alpha_t h_t(x)} \frac{E_{x \approx D} \left[ e^{-f(x) H_{t-1}(x)} \right]}{E_{x \approx D} \left[ e^{-f(x) H_t(x)} \right]} \end{array}$$

这就是上述算法过程中第 (7) 步的由来.

---

R程序示例

这里我们还是以 "churn" 数据集为例，来演示 AdaBoost提升算法的过程.

R中的 adabag包 分别实现了 bagging 方法和 boosting 方法的几种算法，没有安装该包的读者需要先按照包:

> install.packages("adabag")

第一步，加载数据集:

# install.packages("C50")
> library(C50)
# 加载数据
> data(churn)
> 

可以看到此时在内存中有两个对象: churnTest 和 churnTrain .分布为测试集和训练集，你可以在使用它们之前做一些数据预处理的工作，比如说去掉一些对分类没有太大作用的变量；

预处理工作我们在前面讲解决策树的时候已经做过了，所以这里为了简化，我们直接使用原始数据集.

# 使用adaboost算法前需先导包
> library(adabag)
> 
> set.seed(2)
# 利用 adaboost算法训练
> churn.boost = boosting(churn ~., data = churnTrain,mfinal = 10,coeflearn = "Breiman",boos = TRUE,control = rpart.control(maxdepth = 3))
>

boosting()算法的实现是使用的 AdaBoost.M1 和 SAMME 算法，分类器使用的是决策树；详情可使用 help("boosting") 查看.

boosting() 函数的原型为 boosting(formula, data, boos = TRUE, mfinal = 100, coeflearn = 'Breiman', control,...)

formula: 与线性回归一样的公式，~ 符合的左边表示要输出的变量，右边表示预测变量.

data: 数据集，用于 formula

boos: if TRUE (by default), a bootstrap sample of the training set is drawn using the weights for each observation on that iteration. If FALSE, every observation is used with its weights. 暂时笔者也没搞明白这个参数什么意思.

mfinal: 迭代次数，或者是树的生成棵树.

coeflearn: $\alpha$更新公式，如果为 'Breiman'，公式为 $\alpha = \frac{1}{2} \ln \left( \frac{1 - err}{err} \right)$，我们上面的推导就是用的这个公式；如果为 'Freund'，公式为 $\alpha = \ln \left( \frac{1 - err}{err} \right)$.如果为 'Zhu'，公式为 $\alpha = \ln \left( \frac{1 - err}{err} \right) + \ln(nclasses - 1)$

control: 这里可以设置决策树的各个参数.详情可以参考 help("rpart.control").

模型训练好了，下面可以用于预测了:

# 输入测试集进行预测
> churn.boost.pred = predict.boosting(churn.boost,newdata = churnTest)
# 输出测试集预测的混淆矩阵
> churn.boost.pred$confusion
               Observed Class
Predicted Class  yes   no
            no   115 1431
            yes  109   12
# 输出预测误差
> churn.boost.pred$error
[1] 0.07618476
# 可以查看预测结果对象的数据结构
> str(churn.boost.pred)
List of 6
 $ formula  :Class 'formula'  language churn ~ .
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
 $ votes    : num [1:1667, 1:2] 0 0.431 1.473 0.71 0.66 ...
 $ prob     : num [1:1667, 1:2] 0 0.0969 0.3315 0.1597 0.1485 ...
 $ class    : chr [1:1667] "no" "no" "no" "no" ...
 $ confusion: 'table' int [1:2, 1:2] 115 109 1431 12
  ..- attr(*, "dimnames")=List of 2
  .. ..$ Predicted Class: chr [1:2] "no" "yes"
  .. ..$ Observed Class : chr [1:2] "yes" "no"
 $ error    : num 0.0762
>

上面的预测误差为 0.0762，说明预测准确率为 92.38%，模型还算比较好.

若想提高准确率，可以对数据集进行预处理，或者调整决策树的各个参数.

---

小结

到这里 AdaBoost 提升算法就讲完了，希望讲明白了.