机器学习篇

支持向量机

支持向量机(SVM) 是在所有知名的数据挖掘算法中最健壮、最准确的方法之一，主要包括支持向量分类（SVC）和支持向量的回归器（SVR）。

SVM 最初是由 Vapnik 在20世纪90年代发展而来的，该方法建立在统计学习理论的坚实基础上。

SVM 可以从大量训练数据中选出很少的一部分用于模型构建，而且通常维数不敏感.

支持向量分类

SVM 是处理二分类问题的，将数据集分为正例或反例；不过将 SVM 与 决策树结合，可以对数据集进行多分类.

间隔与支持向量

给定训练样本集 $D = \{ (\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\cdots,(\boldsymbol{x}_m,y_m) \},y_i \in \{ -1,+1 \}$，分类学习最基本的想法就是基于训练集 $D$ 在样本空间中找到一个划分超平面，将不同类别的样本分开.但能将训练样本分开的划分超平面可能有很多，如下图所示，我们应该努力去找到哪一个呢？

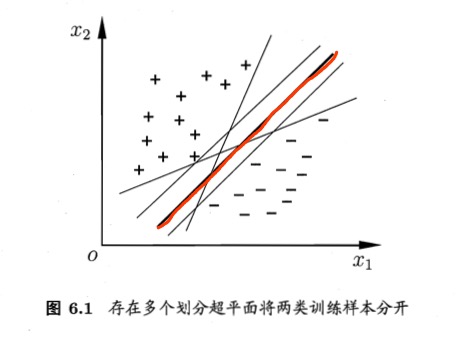
直观上看，应该去找位于两类训练样本“正中间”的划分超平面，如图中红色的那个，因为该划分超平面对训练样本局部扰动的“容忍”性最好.

例如，由于训练集的局限性或噪声的因素，训练集外的样本可能比图中的训练样本更接近两个类的分隔界，这将使许多划分超平面出现错误，而红色的超平面受影响最小.

换言之，这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强.

---

在样本空间中，划分超平面可通过如下线性方程来描述:

$$y = \boldsymbol{w}^T \boldsymbol{x} + b = 0$$ 其中，$\boldsymbol{w} = (w_1;w_2;\cdots;w_d)$ 为法向量，决定了超平面的方向；$b$ 为位移项，决定了超平面与原点之间的距离。显然，划分超平面可被法向量 $\boldsymbol{w}$ 和位移 $b$ 确定.

超平面是纯粹的数学概念，是平面中的直线、空间中的平面的推广，表示欧式空间中维度大于 3 的平面.

法向量是空间解析几何的一个概念，垂直于平面的直线所表示的向量为该平面的法向量。
由于空间内有无数个直线垂直于已知平面，因此一个平面都存在无数个法向量（包括两个单位法向量）。

下面我们将其记为 $(\boldsymbol{w},b)$.样本空间中任意点 $\boldsymbol{x}$ 到超平面 $(\boldsymbol{w},b)$ 的距离可写为:

$$r = \frac{|\boldsymbol{w}^T \boldsymbol{x}+ b|}{||\boldsymbol{w}||}$$

因为点到平面的距离，等于点在平面的方程表达式的值的绝对值 除以 平面的法向量的模.

---

假设超平面 $(\boldsymbol{w},b)$ 能将训练样本正确分类，即对于点 $(\boldsymbol{x}_i,y_i) \in D$，若 $y_i = +1$，则有 $\boldsymbol{w}^T \boldsymbol{x}_i+ b > 0$；若 $y_i = -1$，则有 $\boldsymbol{w}^T \boldsymbol{x}_i+ b < 0$.

令

$$\begin{cases} \boldsymbol{w}^T \boldsymbol{x}_i+ b &\geq& +1, & y_i = +1;\\ \boldsymbol{w}^T \boldsymbol{x}_i+ b &\leq& -1, & y_i = -1 \end{cases}$$

因为 $y_i = \boldsymbol{w}^T \boldsymbol{x}_i+ b$ 总可以变换成 : $1 = \frac{\boldsymbol{w}^T}{y_i} \boldsymbol{x}_i + \frac{b}{y_i} = \boldsymbol{w}'^T \boldsymbol{x}_i+ b'$ 使上式成立.

如下图所示，距离超平面最近的这几个训练样本点使上式的等号成立，它们被称为“支持向量”（support vector），两个异类支持向量到超平面的距离之和为:

$$\gamma = r_+ + r_- = \frac{|\boldsymbol{w}^T \boldsymbol{x}_++ b|}{||w||} + \frac{|\boldsymbol{w}^T \boldsymbol{x}_-+ b|}{||w||} = 2 \times \frac{1}{||w||}$$ 它被称为“间隔”（margin）.

---

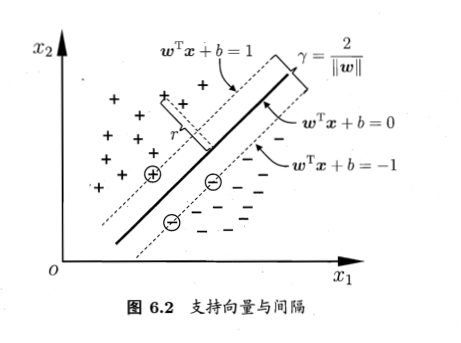
SVM 训练的目的就是为了找到具有“最大间隔”（maximum margin）的划分超平面，也就是要找到能满足如下约束的参数 $\boldsymbol{w}$ 和 $b$，使得 $\gamma$ 最大，即

$$\begin{array} & \max_{\boldsymbol{w},b} \frac{2}{||w||} \\ s.t. \quad y_i(\boldsymbol{w}^T \boldsymbol{x}_i+ b) \geq 1,i = 1,2,\cdots,m \end{array}$$

显然，为了最大化间隔，仅需最大化 $||w||^{-1}$，这等价于最小化 $||w||^2$，于是，原问题转换为对偶问题得:

$$\begin{array} & \min_{\boldsymbol{w},b} \frac{1}{2} ||w||^2 \\ s.t. \quad y_i(\boldsymbol{w}^T \boldsymbol{x}_i+ b) \geq 1,i = 1,2,\cdots,m \end{array} (1)$$ 这就是支持向量机（Support Vector Machine,简称 SVM）的基本模型.

---

对偶问题

我们希望求解上式来得到大间隔划分超平面所对应的模型

$$f(\boldsymbol{x}) = \boldsymbol{w}^T \boldsymbol{x} + b$$ 其中 $\boldsymbol{w}$ 和 $b$ 是模型参数，这是一个凸二次规划（convex quadratic programming）问题，能直接用现成的优化计算包求解，但我们可以有更高效的办法.

对式 (1) 使用拉格朗日乘子法可得到其“对偶问题”（dual problem）.具体来说，对式 (1) 的每条约束条件添加拉格朗日乘子 $\alpha_i \geq 0$，则该问题的拉格朗日函数可写为:

$$L(\boldsymbol{w},b,\boldsymbol{\alpha}) = \frac{1}{2} ||w||^2 + \sum_{i=1}^m \alpha_i (1 - y_i (\boldsymbol{w}^T \boldsymbol{x}_i+ b))$$ 其中 $\boldsymbol{\alpha} = (\alpha_1;\alpha_2;\cdots;\alpha_m)$.

要求 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$ 的极值，需令 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$ 对 $\boldsymbol{w}$ 和 $b$ 的偏导为零可得

$$\begin{array} \frac{\partial L(\boldsymbol{w},b,\boldsymbol{\alpha})}{\partial \boldsymbol{w}} &=& w + (- \sum_{i=1}^m \alpha_i y_i \boldsymbol{x}) = 0 \\ \frac{\partial L(\boldsymbol{w},b,\boldsymbol{\alpha})}{\partial b} &=& 0 + ( - \sum_{i=1}^m \alpha_i y_i ) = 0 \end{array}$$ 将上两式带入 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$，即可将 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$中的 $\boldsymbol{w}$ 和 $b$ 消去，考虑 $\alpha$ 和 $y$ 的约束，将 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$ 展开: $$\begin{array} LL(\boldsymbol{w},b,\boldsymbol{\alpha}) &=& \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m {\alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j} \\&+& \sum_{i=1}^m \alpha_i \\&-& \sum_{i=1}^m \alpha_i y_i \left( \sum_{j=1}^m \alpha_j y_j \boldsymbol{x}_j^T \boldsymbol{x}_i \right) \\&-& \sum_{i=1}^m \alpha_i y_i b \\&=& \sum_{i=1}^m \alpha_i + \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m {\alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j} \\&-& \sum_{i=1}^m \sum_{j=1}^m {\alpha_i \alpha_j y_i y_j \boldsymbol{x}_j^T \boldsymbol{x}_i} + b \times \sum_{i=1}^m \alpha_i y_i \\&=& \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m {\alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j} \end{array}$$ 所以就得到原问题的对偶问题: $$\begin{array} & \max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m {\alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j} \\ s.t. \sum_{i=1}^m \alpha_i y_i = 0, \alpha_i \geq 0,i = 1,2,\cdots,m \end{array}$$ 解出 $\boldsymbol{\alpha}$ 后，求出 $\boldsymbol{w}$ 和 $b$ 即可得到模型: $$\begin{array} \boldsymbol{w} &=& \sum_{i=1}^m \alpha_i y_i \boldsymbol{x}_i \\ b &=& \frac{1}{M} \sum_{m \in M} \left( y_m - \sum_{i \in M} \alpha_i y_i \boldsymbol{x}_i^T \boldsymbol{x}_m \right) \\ f(\boldsymbol{x}) &=& \boldsymbol{w}^T \boldsymbol{x} + b \\&=& \sum_{i=1}^m \alpha_i y_i \boldsymbol{x}_i^T \boldsymbol{x} + b \end{array}$$

---

问题就变成了如何求解 $\boldsymbol{\alpha}$，从对偶问题的目标函数可知，这是一个二次规划问题，可使用通用的二次规划算法来求解；然而，该问题的规模正比于训练样本数 $m$，这会在实际应用中造成很大的开销，为了避开这个障碍，人们通过利用问题本身的特性，提出了很多高效的算法，SMO(Sequential Minimal Optimization) 是其中一个著名的代表.

SMO 的基本思路是先固定 $\alpha_i$ 之外的所有参数，然后求 $\alpha_i$ 上的极值.由于存在约束 $\sum_{i=1}^m \alpha_i y_i = 0$，若固定 $\alpha_i$ 之外的其他变量，则 $\alpha_i$ 可由其他变量导出.于是，$SMO$ 每次选择两个变量 $\alpha_i$ 和 $\alpha_j$，并固定其他参数，这样，在参数初始化后，$SMO$ 不断执行如下几个步骤直至收敛:

1. 随机初始化 $\alpha_k,k = 1,2,\cdots,m$，并保证 $\sum_{i=1}^m \alpha_i y_i = 0$ 即可

2. 选取一对需更新的变量 $\alpha_i$ 和 $\alpha_j$

3. 固定除 $\alpha_i$ 和 $\alpha_j$ 以外的其他 $\alpha_k$；由于有约束 $\sum_{i=1}^m \alpha_i y_i = 0$，于是有

   $$\alpha_i y_i + \alpha_j y_j = c,\alpha_i \geq 0,\alpha_j \geq 0 \\ c = -\sum_{k \neq i,j} \alpha_k y_k$$ 此时由于其他 $\alpha_k$是固定的，所以 $c$ 相对于 $\alpha_i$ 和 $\alpha_j$ 来说就是常数。

   那么将 $\alpha_i$ 用 $\alpha_j$ 表示为 $\alpha_i = \frac{c - \alpha_j y_j}{y_i}$ ，带入到目标函数 $L(\boldsymbol{w},b,\boldsymbol{\alpha})$，则此时的目标函数就是只关于变量 $\alpha_j$ 的一元函数了，在此条件下便可对目标函数求极值，解出 $\alpha_j$，此时 $\alpha_i$ 也求出来了；

   到此一轮迭代结束，转到第 $2$ 步继续选取一对需要更新的变量 $\alpha_i^{'}$ 和 $\alpha_j^{'}$ 继续迭代.

   迭代的终止条件可以为前后两次迭代 $\boldsymbol{\alpha}$ 总体的变化不超过一定的阈值，且迭代次数小于设定的最大迭代次数.

最后一个问题是 如何选取一对 $\alpha_i$ 和 $\alpha_j$ 进行更新？

我们的目标是使目标函数的值变化的最快，以最少的迭代次数收敛到极值；所以 SMO 采用了一种启发式方法：使选取的两变量所对应样本之间的间隔最大.

比如 $\boldsymbol{x}_i$ 与 $\boldsymbol{x}_j$ 之间的间隔最大（距离最大），则就取对应的 $\alpha_i$ 和 $\alpha_j$ 做迭代.

因为一个 $\alpha$ 对应一个样本

这种启发式方法的直观解释是：这样选取的两个变量有很大的差别，与对两个相似的变量进行更新相比，对它们进行更新会带给目标函数值更大的变化.

---

核函数

一般来说按上面的步骤就可以解决训练样本线性可分的问题了，但是当遇到训练样本线性不可分时呢，比如向下图这种“异或”问题？

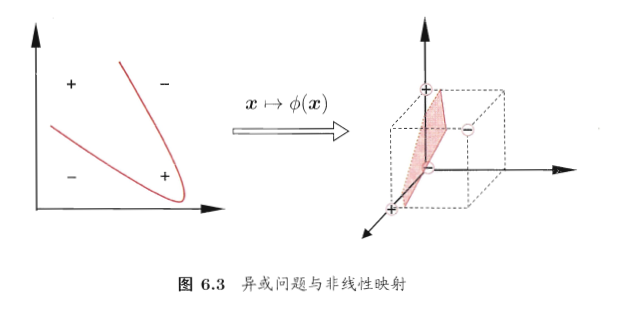
对于这样的问题，可以将样本从原始空间映射到一个更高维的特征空间，使得样本在这个更高维的特征空间中是线性可分的，而且具理论证明，如果原始空间是有限维，即属性数量有限，都可以映射到高维使样本线性可分。

---

令 $\phi(\boldsymbol{x})$ 表示将 $\boldsymbol{x}$ 映射后的特征向量，于是，在特征空间中划分超平面所对应的模型可表示为:

$$f(\boldsymbol{x}) = \boldsymbol{w}^T \phi(\boldsymbol{x}) + b$$ 其中 $\boldsymbol{w}$ 和 $b$ 是模型的参数，含义与本篇上面部分一致，则 SVM的优化目标为 $$\begin{array} & \min_{\boldsymbol{w},b} \frac{1}{2} ||\boldsymbol{w}||^2 \\ s.t. \quad y_i (\boldsymbol{w}^T \phi(\boldsymbol{x}_i) + b) \geq 1,i = 1,2,\cdots,m \end{array}$$ 其对偶问题是: $$\begin{array} & \max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j) \\ s.t. \quad \sum_{i=1}^m \alpha_i y_i = 0,\alpha_i \geq 0,i = 1,2,\cdots,m \end{array}$$ 从上式可以看成，求解需要计算 $\phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$，这是样本 $\boldsymbol{x}_i$ 与 $\boldsymbol{x}_j$ 映射到特征空间之后的内积，由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算 $\phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$ 通常是困难的。

幸运的是，这里 $\phi(\boldsymbol{x})$ 只在计算 $\phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$ 时参与了计算，所以为了避开这个障碍，若能找到一个函数:

$$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = <\phi(\boldsymbol{x}_i),\phi(\boldsymbol{x}_j)> = \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$$ 即 $\boldsymbol{x}_i$ 和 $\boldsymbol{x}_j$ 在特征空间的映射的内积等于它们在原始样本空间中函数 $\kappa(\cdot,\cdot)$ 的值.

有了这样的函数，目标就可以改写成:

$$\begin{array} & \max_{\alpha} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) \\ s.t. \quad \sum_{i=1}^m \alpha_i y_i = 0,\alpha_i \geq 0,i = 1,2,\cdots,m \end{array}$$

求解后得:

$$\begin{array} ff(\boldsymbol{x}) &=& \boldsymbol{w}^T \boldsymbol{x} + b \\&=& \sum_{i=1}^m \alpha_i y_i \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j) + b \\ &=& \sum_{i=1}^m \alpha_i y_i \kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) + b \end{array}$$ 这里的函数 $\kappa(\cdot,\cdot)$ 就是“核函数”（kernel function）了，其中，上式称为“支持向量展式”，显示出模型最优解可通过训练样本的核函数展开.

---

上面只有核函数的定义，而没有具体的形式，那什么样的函数才是核函数呢？

根据核函数的定义，要验证一个函数是否是核函数，需要验证该函数在任意数据上的“核矩阵”总是半正定的，这需要大量的计算，所以一般我们是直接使用几种常用的核函数:

名称	表达式	参数
线性核	$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = \boldsymbol{x}_i^T \boldsymbol{x}_j$
多项式核	$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = (\boldsymbol{x}_i^T \boldsymbol{x}_j)^d$	$d \geq 1$ 为多项式的次数
高斯核	$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = \exp \left (-\frac{||\boldsymbol{x}_i - \boldsymbol{x}_j||^2}{2 \sigma^2} \right)$	$\sigma > 0$ 为高斯核的带宽(width)
拉普拉斯核	$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = \exp \left (-\frac{||\boldsymbol{x}_i - \boldsymbol{x}_j||^2}{\sigma} \right)$	$\sigma > 0$
Sigmoid 核	$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = \tanh(\beta \boldsymbol{x}_i^T \boldsymbol{x}_j + \theta)$	tanh 为双曲正切函数，$\beta >0,\theta < 0$

核矩阵是样本之间通过核函数映射之后得到的，每两个样本之间进行一次核函数影射，故N个样本就构成N*N维的核矩阵。

人们把这些点的内积放在了一个矩阵里,并叫它核矩阵,核矩阵定义了世界的分类。在这个核矩阵里,矩阵里每个点的值是两个X世界点的线性内积。

此外，还可通过函数组合得到，例如:

• 若 $\kappa_1$ 和 $\kappa_2$ 为核函数，则对于任意正数 $\gamma_1、\gamma_2$，其线性组合

  $$\gamma_1 \kappa_1 + \gamma_2 \kappa_2$$ 也是核函数

• 若 $\kappa_1$ 和 $\kappa_2$ 为核函数，则核函数的直积

  $$\kappa_1 \otimes \kappa_2(\boldsymbol{x},\boldsymbol{z}) = \kappa_1(\boldsymbol{x},\boldsymbol{z}) \kappa_2(\boldsymbol{x},\boldsymbol{z})$$ 也是核函数

• 若 $\kappa_1$ 为核函数，则对于任意函数 $g(\boldsymbol{x})$，

  $$\kappa(\boldsymbol{x},\boldsymbol{z}) = g(\boldsymbol{x}) \kappa_1(\boldsymbol{x},\boldsymbol{z}) g(\boldsymbol{z})$$ 也是核函数

核函数的使用进而可以演变成一种核方法，即通过“核化”（引入核函数）来将线性学习器扩展成非线性学习器，使得

$$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) = <\phi(\boldsymbol{x}_i),\phi(\boldsymbol{x}_j)> = \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$$ 即 $\boldsymbol{x}_i$ 和 $\boldsymbol{x}_j$ 在特征空间的映射的内积等于它们在原始样本空间中函数 $\kappa(\cdot,\cdot)$ 的值.

关于核方法的理论比较复杂，若读者有兴趣可以自行查阅相关资料进行学习，本教程主要是讲解算法的基础.

---

软间隔

前面我们讲了存在一个超平面能将样本集中不同类的样本完全划分开，但是，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；

就算恰好找到了某个核函数使得训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合导致的.

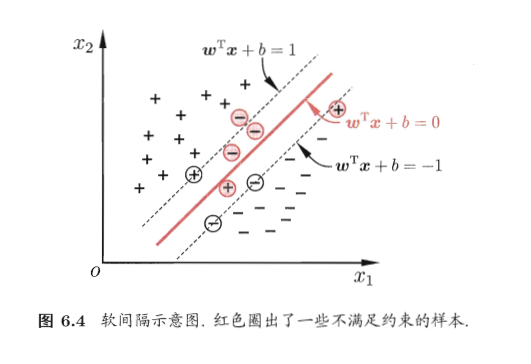
为了适当的改善该问题，我们引入“软间隔”（soft margin）的概念。即上面的“硬间隔”是要求所有样本都正确分类，而我们现在允许某些样本不满足约束:

$$y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) < 1$$ 尽管是允许一部分样本不满足约束，但是要求这类样本越少越好，于是优化目标可写成: $$\begin{array} & \min_{\boldsymbol{w},b} \frac{1}{2} ||\boldsymbol{w}||^2 + C \sum_{i=1}^m l_{0/1} (y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) -1) \end{array}$$ 其中 $C > 0$ 是一个常数，$l_{0/1}$ 是“0/1 损失函数” $$l_{0/1}(z) = \begin{cases} 1, & if \quad z < 0;\\ 0, & otherwise \end{cases}$$ 其中 $z = y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) -1 < 0$ 表示样本 $(\boldsymbol{x}_i,y_i)$ 未分类正确，应该受到惩罚，所以 $C$ 是惩罚因子.

---

然而，上面的 $l_{0/1}$ 损失函数非凸、非连续，数学性质不太好，优化目标不太容易求解；于是人们找了一些函数来“替代损失”，替代损失函数一般具有比较好的数学性质，下面是三种常用的替代损失函数:

• hinge 损失: $\quad l_{hinge}(z) = \max(0, 1 - z)$
• 指数损失: $\quad l_{exp}(z) = \exp(-z)$
• 对率损失: $\quad l_{log}(z) = \log(1 + \exp(-z))$

若采用 hinge 损失，则优化目标可以写成:

$$\begin{array} & \min_{\boldsymbol{w},b} \frac{1}{2} ||\boldsymbol{w}||^2 + C \sum_{i=1}^m \max(0,1 - (y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) -1)) \end{array}$$

若我们引入“松弛变量”（slack variables）$\xi_i \geq 0$，每个样本都对应着一个松弛变量，用以表征该样本不满足“硬间隔”约束的程度，也即是损失函数的值；

于是优化目标改写成:

$$\begin{array} & \min_{\boldsymbol{w},b,\xi_i} \frac{1}{2} ||\boldsymbol{w}||^2 + C \sum_{i=1}^m \xi_i \\ s.t. \quad y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) \geq 1 - \xi_i \\ \qquad \quad \xi_i \geq 0,i = 1,2,\cdots,m \end{array}$$ 这就是常用的“软间隔支持向量机”.

---

显然上式也是一个二次规划问题，于前面“硬间隔”的解法类似，通过拉格朗日乘子法得到拉格朗日函数:

$$\begin{array} & L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{u}) &=& \frac{1}{2} ||\boldsymbol{w}||^2 + C \sum_{i=1}^m \xi_i \\ &+& \sum_{i=1}^m \alpha_i (1 - \xi_i - y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b)) \\ &-& \sum_{i=1}^m \mu_i \xi_i \end{array}$$ 其中 $\alpha_i \geq 0,\mu_i \geq 0$ 是拉格朗日乘子，分别对应着优化目标函数的两个约束条件.

剩下的就是 $L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{u})$ 对 $\boldsymbol{w},b,\boldsymbol{\xi}$ 求偏导，常规的拉格朗日极值解法:

$$\begin{array} & \boldsymbol{\omega} &=& \sum_{i=1}^m \alpha_i y_i \boldsymbol{x}_i \\ 0 &=& \sum_{i=1}^m \alpha_i y_i \\ C &=& \alpha_i + \mu_i \end{array}$$ 将上面三式带入$L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{u})$，则优化目标的对偶问题得: $$\begin{array} & \max_{\boldsymbol{\alpha}} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j \\ s.t. \quad \sum_{i=1}^m \alpha_i y_i = 0, \\ \qquad 0 \leq \alpha_i \leq C,i = 1,2,\cdots,m \end{array}$$

因为 $\alpha_i,\mu_i$ 都需要大于等于 0，且 $C = \alpha_i + \mu_i$，所以得 $0 \leq \alpha_i \leq C,\quad 0 \leq \mu \leq C$

通过求解上式，就能解出 $\boldsymbol{\alpha}$，然后就能解出 $\boldsymbol{w}$.

对比上式与“硬间隔”下的对偶问题，区别仅在于对偶变量的约束不同，即“硬间隔”的是 $0 \leq \alpha_i$，“软间隔”的约束是 $0 \leq \alpha_i \leq C$，于是求解方法同“硬间隔”一样.

---

到这里唯一有疑问的就是 $b$ 的求解，在“硬间隔”中，有 $b_i = y_i - \boldsymbol{w}^T \boldsymbol{x}_i$ 即可直接求出 $b$；但是对于“软间隔”呢？

上述含有不等式约束的最优化问题要满足KKT条件，KKT条件要求:

$$\begin{cases} \alpha_i \geq 0, \mu_i \geq 0 \\ y_i f(\boldsymbol{x}_i) - 1 + \xi_i \geq 0, \\ \alpha_i (y_i f(\boldsymbol{x}_i) - 1 + \xi_i) = 0, \\ \xi_i \geq 0,\mu_i \xi_i = 0 \end{cases}$$ 于是对任意的训练样本 $(\boldsymbol{x}_i,y_i)$，总有 $\alpha_i = 0$ 或者 $y_i f(\boldsymbol{x}_i) = 1 - \xi_i$.

• 若 $\alpha_i = 0$ ，则样本不会对 $f(\boldsymbol{x})$ 有任何影响；

• 若 $\alpha_i > 0$，则必有 $y_i f(\boldsymbol{x}_i) = 1 - \xi_i$，即该样本是支持向量；

于是在 $\alpha_i > 0$ 的条件下，解 $y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) = 1 - \xi_i$ 可求出 $b$；但是这里的 $\xi_i$ 不知道，此时的 $b$ 是无法求的；但是若 $\xi_i = 0$，则 $b$ 就很容易求了。

由 $\mu_i \xi_i = 0$ 可知，要想 $\xi_i = 0$，则要求 $\mu_i > 0$；又因为 $C = \alpha_i + \mu_i$，若 $\mu_i > 0$，则必有 $\alpha_i < C$，此时表示样本恰好在最大间隔边界上，由此可看出软间隔支持向量机的最终模型仅与支持向量有关.

总结来说，要求 $0 < \alpha_i < C$，此时 $y_i (\boldsymbol{w}^T \boldsymbol{x}_i + b) = 1$ 即可解出 $b$ ；

$C$ 是已知的，事先给定的一常数，为惩罚因子，C越大，越不能容忍噪声，但也可能会导致过拟合。

---

正则化

笔者在看深度神经网络的时候，也会经常要设置正则化项，一直不明白什么是正则化项，在看《机器学习》SVM 的这部分的时候终于明白了.

如上介绍的，我们可以用其他的“替代损失”函数来替换 $l_{0/1}$ 损失函数，从而得到其他的学习模型，这些模型的性质与所用的替代函数直接相关，但它们具有一个共性: 优化目标中的第一项用来描述划分超平面的“间隔”大小，另一项 $\sum_{i=1}^m l(f(\boldsymbol{x}_i),y_i)$ 用来表述训练集上的误差，这可以写成一般形式:

$$\min_{f} \Omega(f) + C \sum_{i=1}^m l(f(\boldsymbol{x}_i),y_i)$$ 其中，
第一项 $\Omega(f)$ 称为“结构风险”（structural risk），用来描述模型 $f$ 的某些性质；

第二项 $\sum_{i=1}^m l(f(\boldsymbol{x}_i),y_i)$ 称为“经验风险”（empirical risk），用于描述模型与训练数据的契合度；

$C$ 用于对二者进行折中；

从经验风险最小化的角度来看，$\Omega(f)$ 表述了我们希望获得具有何种性质的模型（例如希望获得复杂度较小的模型），这为引入领域的知识和用户意图提供了途径；另一方面，该信息有助于削减假设空间，从而降低了最小化训练误差的过拟合风险.

从这个角度来看，上述目标式就被称为“正则化”（regularization）问题，$\Omega(f)$ 称为正则化项，$C$ 则称为正则化常数.

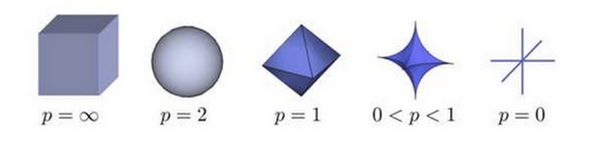
$L_p$ 范数（norm）是常用的正则化项，其中 $L_2$ 范数 $||w||^2$ 倾向于 $w$ 的分量取值尽量均衡，即非零分量个数尽量稠密，而 $L_0$ 范数 $||w||^0$ 和范数 $L_1$ 范数 $||w||^1$ 则倾向于 $w$ 的分量尽量稀疏，即非零分量个数尽量少.

正则化这里就解释了为什么最开始的优化目标是 $\min_{w} \frac{1}{2} ||w||^2$ ，使用的是 $L_2$ 范数，其中 $\frac{1}{2}$ 是为了后面求导时消除掉 $w$ 的系数而添加的.

范数 是测度论里的概念，可以单纯的理解为“距离”，定义为 $L_p = \sqrt[p]{\sum_{i = 1}^n x_i^p}$，其中，$\boldsymbol{x} = (x_1,x_2,\cdots,x_n)$ 是空间中的一个点.

其中，$p = 2$ 时就是表示的欧式距离.

不同的 $p$ 值几何意义如图:

---

R 程序演示

我们用 libsvm 的 R 版本来做演示，使用记录客户流失率的 churn 数据集来训练.

churn数据集在 "C50" 包中，首先加载 churn 数据集:

# install.packages("C50")
> library(C50)
> data(churn)
>

可以看到在内存中有两个变量 churnTest和churnTrain，分别表示测试集和训练集，具体详情可以通过 help("churnTrain") 来查看；每条记录包含 19 个预测变量，"churn"变量为输出变量，标记为"yes/no".

---

为了顺便给读者演示如何构建自己的训练集和测试集，笔者这里先将上面的测试集和训练集合并，然后再按比例拆散成训练集和测试集:

# 合并测试集和训练集
> churnData = rbind(churnTrain,churnTest)
# 查看数据集的结构
> str(churnData)
'data.frame':   5000 obs. of  20 variables:
 $ state                        : Factor w/ 51 levels "AK","AL","AR",..: 17 36 32 36 37 2 20 25 19 50 ...
 $ account_length               : int  128 107 137 84 75 118 121 147 117 141 ...
 .......
 $ total_day_minutes            : num  265 162 243 299 167 ...
 ...........
 $ number_customer_service_calls: int  1 1 0 2 3 0 3 0 1 0 ...
 $ churn                        : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...
>

一般我们在构建测试集和训练集之前要对原始数据进行预处理，包括数据清洗（缺失数据、噪音数据），还有变量的选取，去掉一些对预测没太大影响的变量；

下面使用 "rminer"包对变量敏感度分析，来演示变量的选取:

#install.packages("rminer")
> library(rminer)
# 用svm对原始数据进行训练，得到初始模型
> model = fit(churn ~.,churnData,model = "svm")
# 基于敏感度检测，对变量重要度进行排序
> VariableImportance = Importance(model,churnData,method = "sensv")
# 绘制根据变量重要性排序后的变量重要度图
> L = list(runs = 1,sen = t(VariableImportance$imp),sresponses = VariableImportance$sresponses)
> mgraph(L,graph = "IMP",leg = names(churnData),col = "gray",Grid = 10)
>

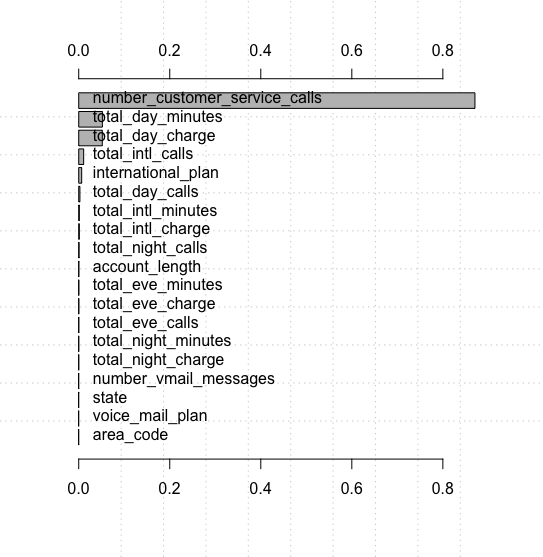
从图中可以看成，后面的 10 多个变量对SVM分类来说基本没什么影响，为了降低模型的复杂度和计算量，在训练和测试过程中可以剔除这些变量.

# 我们选取前 7 个预测变量来训练和测试
> churnData = churnData[,c("number_customer_service_calls","total_day_minutes","total_day_charge","total_intl_calls","international_plan","total_day_calls","total_intl_minutes","churn")]
> set.seed(2)
# 随机生成数据集的 70% 作为训练，30% 作为测试
> ind = sample(2,nrow(churnData),replace = TRUE,prob = c(0.7,0.3))
# ind 的标号与 prob = (x,y) 中x,y的索引一致
> trainset = churnData[ind == 1,]
> testset = churnData[ind == 2,]
> 

这样训练集和测试集都制作好了，分别包含 7 个预测变量，一个目标变量.

---

下面就可以训练svm模型了:

# kernel 是核函数，cost 是惩罚因子
> model = svm(churn ~., data = trainset,kernel = "radial",cost = 1,gamma = 1/ncol(trainset))
# 查看svm训练好的模型
> summary(model)
Call:
svm(formula = churn ~ ., data = trainset, kernel = "radial", cost = 1, gamma = 1/ncol(trainset))
Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  radial 
       cost:  1 
      gamma:  0.125 
Number of Support Vectors:  950
 ( 510 440 )
Number of Classes:  2 
Levels: 
 yes no
>

预测:

> svm.pred = predict(model,testset[,!names(testset) %in% c("churn")])
# 生成混淆矩阵表
> svm.table = table(svm.pred,testset$churn)
> svm.table
svm.pred  yes   no
     yes   81   27
     no   133 1280
# 计算分类一致性系数
> classAgreement(svm.table)
$diag
[1] 0.894806
$kappa
[1] 0.451321
$rand
[1] 0.8116198
$crand
[1] 0.3925012
> 

上面的 svm.table 输出解释下：svm.pred预测为 "yes" 的 $(81+27) = 108$ 例中，真实值为 "yes" 的有 81 例，为 "no" 的有 27 例；也就是说预测为 "yes" 的正确了 81 例.

其中 classAgreement(svm.table) 的 $diag 就是分类准确度.

或者可以输出混淆矩阵来查看分类结果:

# install.packages("caret")
> library(caret)
# 输出混淆矩阵
> confusionMatrix(svm.table)
Confusion Matrix and Statistics
svm.pred  yes   no
     yes   81   27
     no   133 1280
               Accuracy : 0.8948          
                 95% CI : (0.8783, 0.9098)
    No Information Rate : 0.8593          
    P-Value [Acc > NIR] : 2.146e-05       
                  Kappa : 0.4513          
 Mcnemar's Test P-Value : < 2.2e-16       
            Sensitivity : 0.37850         
            Specificity : 0.97934         
         Pos Pred Value : 0.75000         
         Neg Pred Value : 0.90587         
             Prevalence : 0.14070         
         Detection Rate : 0.05325         
   Detection Prevalence : 0.07101         
      Balanced Accuracy : 0.67892         
       'Positive' Class : yes             
> 

从混淆矩阵的输出中可以看成，Accuracy精度为 0.8948

---

若想调整支持向量机，除了选择不同的特征集和核函数，还可以借助调整参数 gamma 以及惩罚因子来调整支持向量机的性能.

我们可以用 tune.svm()函数来循环检验不同参数组合的效果，从而可以方便的选出最优的参数组合.

# 循环遍历 cost 和 gamma 的不同组合，生成不同的模型
> tuned = tune.svm(churn ~.,data = trainset,gamma = 10^(-6:0),cost = 10^(-1:2))
> summary(tuned)
Parameter tuning of ‘svm’:
- sampling method: 10-fold cross validation 
- best parameters:
 gamma cost
   0.1   10
- best performance: 0.09025721 
- Detailed performance results:
   gamma  cost      error  dispersion
1  1e-06   0.1 0.14170724 0.010228576
2  1e-05   0.1 0.14170724 0.010228576
3  1e-04   0.1 0.14170724 0.010228576
4  1e-03   0.1 0.14170724 0.010228576
......
26 1e-02 100.0 0.10519974 0.018167027
27 1e-01 100.0 0.09169151 0.011437367
28 1e+00 100.0 0.14860545 0.018521885
> 

循环遍历 cost 从0.1 ~ 100，gamma 从10^(-6) 到 1的不同组合，从summary(tuned)的输出结果可以看出这种排列组合的方式.

# 使用最优参数进行重新训练 svm 模型
> model.tuned = svm(churn ~.,data = trainset,gamma = tuned$best.parameters$gamma,cost = tuned$best.parameters$cost)
# 查看最优模型
> summary(model.tuned)
Call:
svm(formula = churn ~ ., data = trainset, gamma = tuned$best.parameters$gamma, cost = tuned$best.parameters$cost)
Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  radial 
       cost:  10 
      gamma:  0.1 
Number of Support Vectors:  840
 ( 459 381 )
Number of Classes:  2 
Levels: 
 yes no
> 

下面有这时的最优模型进行预测:

# 用新模型预测
> svm.tuned.pred = predict(model.tuned,testset[,!names(testset) %in% c("churn")])
> svm.tuned.table = table(svm.tuned.pred,testset$churn)
# 输出混淆矩阵
> confusionMatrix(svm.tuned.table)
Confusion Matrix and Statistics
svm.tuned.pred  yes   no
           yes  102   28
           no   112 1279
               Accuracy : 0.908          
                 95% CI : (0.8923, 0.922)
    No Information Rate : 0.8593         
    P-Value [Acc > NIR] : 5.346e-09      
                  Kappa : 0.5446         
 Mcnemar's Test P-Value : 2.303e-12      
            Sensitivity : 0.47664        
            Specificity : 0.97858        
         Pos Pred Value : 0.78462        
         Neg Pred Value : 0.91948        
             Prevalence : 0.14070        
         Detection Rate : 0.06706        
   Detection Prevalence : 0.08547        
      Balanced Accuracy : 0.72761        
       'Positive' Class : yes            
>

精度为 0.908，相比于之前的结果，效果有提升.

---

小结

到此 SVM 就讲完了.