机器学习篇

BP神经网络

本篇会详细的讲解BP神经网络的原理，以及算法推导过程，BP神经网络的算法优缺点以及如何改进，最后会以一个实际的例子应用R语言编程来演示BP神经网络的过程

BP神经网络的结构

基本BP算法包括两个方面：信号的前向传播和误差的反向传播。即计算实际输出时按从输入到输出的方向进行，而权值和阈值的修正从输出到输入的方向反馈

---

假设给定训练集 $D = \{(\boldsymbol{x}_1,\boldsymbol{y}_1),(\boldsymbol{x}_2,\boldsymbol{y}_2),\cdots,(\boldsymbol{x}_m,\boldsymbol{y}_m)\},\ \boldsymbol{x}_m \in R^d,\ \boldsymbol{y}_i \in R^l$，即输入示例由 $d$ 个属性描述，输出 $l$ 维实值向量。

给出了一个拥有$d$个输入神经元，$l$个输出神经元，$q$个隐含层神经元的多层前馈网络结构，如下图所示:

其中:
输入向量: $\boldsymbol{x} = (x_1,\cdots,x_i,\cdots,x_d)$
隐含层输入向量: $\boldsymbol{\alpha} = (\alpha_1,\cdots,\alpha_h,\cdots,\alpha_q)$
隐含层输出向量: $\boldsymbol{b} = (b_1,\cdots,b_h,\cdots,b_q)$
输出层输入向量: $\boldsymbol{\beta} = (\beta_1,\cdots,\beta_j,\cdots,\beta_l)$
输出层输出向量: $\boldsymbol{\hat{y}} = (\hat{y}_1,\cdots,\hat{y}_j,\cdots,\hat{y}_l)$
输入层第$i$个神经元与隐含层第$h$个神经元之间的连接权值: $v_{ih}$
隐含层第$h$个神经元与输出层第$j$个神经元之间的连接权值: $w_{hj}$
隐含层神经元的阈值向量: $\boldsymbol{\gamma} = (\gamma_1,\cdots,\gamma_h,\cdots,\gamma_q)$
输出层神经元的阈值向量: $\boldsymbol{\theta} = (\theta_1,\cdots,\theta_j,\cdots,\theta_l)$
样本数据个数: $k = 1,2,\cdots,m$
激活函数: $f(x) = \frac{1}{1+e^{-x}}$ 为Sigmoid函数

如前篇所述，激活函数不只有Sigmoid函数一种，还有高斯函数、阶跃函数等等可选，只是由于Sigmoid函数性质比较好，即$f(x)' = f(x)\left(1-f(x)\right)$，所以我们一般采用Sigmoid函数作为激活函数

---

BP神经网络的标准学习算法

这里假设隐含层和输出层的激活函数都使用Sigmoid函数

网络初始化

给个连接权值分别赋一个区间 $(-1,1)$内的随机数 : 为了将连接权值归一化到 $(-1,1)$，方便计算

设定误差函数 $E_k$ : 一般选样本的均方误差，有的选“正则化”的均方误差

给定计算精度值 $\epsilon$ : 当误差函数的值小于计算精度时，代表网络训练达到目标，可停止学习

设置最大学习次数 $M$ : 防止出现网络不收敛 (或者叫不稳定) 的情况，当迭代次数超过 $M$则网络停止学习，但不代表网络已达到目标

---

正向传播过程

随机选取训练例 $(\boldsymbol{x}_k,\boldsymbol{y}_k)$，假定神经网络的输出为 $\hat{\boldsymbol{y}}_k = (\hat{y}_1^k,\hat{y}_2^k,\cdots,\hat{y}_l^k)$

则有:
第 $h$个隐含层神经元的输入: $\alpha_h = \sum_{i=1}^d{v_{ih}x_i}$

第 $h$个隐含层神经元的输出: $b_h = f(\alpha_h - \gamma_h)$

第 $j$个输出层神经元的输入: $\beta_j = \sum_{h=1}^q{w_{hj}b_h}$

第 $h$个输出层神经元的输出: $\hat{y}_j^k = f(\beta_j - \theta_j)$

则网络在 $(\boldsymbol{x}_k,\boldsymbol{y}_k)$ 上的均方误差为:

$$E_k = \frac{1}{2}\sum_{j=1}^l{(\hat{y}_j^k - y_j^k)^2}$$

---

逆向反馈过程

BP算法基于梯度下降(gradient descent)策略，以目标的负梯度方向对参数进行调整。因为正梯度方向是增长最快的方向，则负梯度方向就是减少最快的方向，我们要让误差函数以最快的速度减小

---

结论性的参数调整公式

网络中有 $(d+l+1)q + l$个参数需要确定: 输入层到隐含层的 $d \times q$个权值、隐含层到输出层的 $q \times l$个权值、$q$个隐含层神经元的阈值、$l$个输出层神经元的阈值

BP是一个迭代学习算法，任意参数 $v$ 的更新估计式为

$$v \leftarrow v + \Delta v$$

具体来说:

$$\begin{cases} \Delta w_{hj} &=& \eta g_j b_h \\ \Delta \theta_j &=& -\eta g_j \\ \Delta v_{ih} &=& \eta e_{h} x_i \\ \Delta \gamma_h &=& -\eta e_h \\ g_j &=& \hat{y}_j^k(1 - \hat{y}_j^k)(y_j^k - \hat{y}_j^k) \\ e_h &=& b_h(1 - b_h)\sum_{j=1}^l{(w_{hj}g_j)} \end{cases}$$

其中: $\eta \in (0,1)$ 为学习速率；$\eta$ 过小时，整个网络迭代的收敛速度就过慢；$\eta$ 过大时，网络的收敛速度就比较快，但同时容易出现震荡现象而无法收敛

---

连接权值调整公式的推导过程

因为我们要以目标的负梯度方向对参数进行调整，所以对隐含层与输出层之间的连接权值有

$$\Delta w_{hj} = -\eta \frac{\partial E_k}{\partial w_{hj}}$$
注意到 $w_hj$先影响到第 $j$个输出层神经元的输入值 $\beta_j$，$\beta_j$在影响到其输出值 $\hat{y}_j^k$，然后再影响到 $E_k$，所以有 $$\frac{\partial E_k}{\partial w_{hj}} = \frac{\partial E_k}{\partial \hat{y}_j^k}.\frac{\partial \hat{y}_j^k}{\partial \beta_j}.\frac{\partial \beta_j}{\partial w_{hj}}$$ 这里利用到了微分的链式法则，根据正向传播过程中各参数的定义，显然有 $$\begin{cases} \frac{\partial \beta_j}{\partial w_{hj}} &=& b_h \\ \frac{\partial \hat{y}_j^k}{\partial \beta_j} &=& f'(\beta_j - \theta_j) \\ \frac{\partial E_k}{\partial \hat{y}_j^k} &=& (\hat{y}_j^k - y_j^k) \end{cases}$$ 由于我们使用的激活函数是Sigmoid函数，该函数有个很好的性质，即 $$f'(x) = f(x)(1 - f(x))$$

因为

$$f'(x) = \left( \frac{1}{(1+e^{-x})} \right)' \\ = -\frac{1}{(1+e^{-x})^2}(1+e^{-x})' \\ = -\frac{1}{(1+e^{-x})^2}e^{-x}(-1) \\ = \frac{1}{1+e^{-x}}\frac{e^{-x}}{1+e^{-x}} \\ = f(x)(1-f(x))$$
则$\frac{\partial \hat{y}_j^k}{\partial \beta_j} = \hat{y}_j^k(1 - \hat{y}_j^k)$.

所以有

$$\Delta w_{hj} = -\eta\frac{\partial E_k}{\partial w_{hj}} = -\eta (\hat{y}_j^k - y_j^k) \hat{y}_j^k(1 - \hat{y}_j^k) b_h$$ 令 $$g_j = -\frac{\partial E_k}{\partial \hat{y}_j^k}.\frac{\partial \hat{y}_j^k}{\partial \beta_j} = (y_j^k - \hat{y}_j^k) \hat{y}_j^k(1 - \hat{y}_j^k)$$ 则 $$\Delta w_{hj} = \eta g_j b_h$$

---

下面推导输入层与隐含层的连接权值调整公式:

$$\Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}} = -\eta \frac{\partial E_k}{\partial b_h}.\frac{\partial b_h}{\partial \alpha_h}.\frac{\partial \alpha_h}{\partial v_{ih}}$$ 由正向传播过程各参数的定义可知: $$\begin{cases} \frac{\partial b_h}{\partial \alpha_h} &=& f'(\alpha_h - \gamma_h) = b_h(1 - b_h) \\ \frac{\partial \alpha_h}{\partial v_{ih}} &=& x_i^k \end{cases}$$ 而$\frac{\partial E_k}{\partial b_h}$的计算就麻烦点，因为从 $\beta_j = \sum_{h=0}^q{w_{hj} b_h}$有个值求和汇总的过程，所以误差反向传播的时候也要有个误差对 $w_{hj}$的影响汇总到对 $b_h$误差调整的过程，于是有 $$\frac{\partial E_k}{\partial b_h} = \sum_{j=1}^l{\left( \frac{\partial E_k}{\partial \beta_j}.\frac{\partial \beta_j}{\partial b_h} \right)} = \sum_{j=1}^l{(-g_j w_{hj})}$$ 我们令 $$e_h = -\frac{\partial E_k}{\partial b_h}.\frac{\partial b_h}{\partial \alpha_h} = b_h (1-b_h) \sum_{j=1}^l{(g_j w_{hj})}$$
所以总结起来得 $$\Delta v_{ih} = -\eta b_h(1-b_h) x_i^k \sum_{j=1}^l{(-g_j w_{hj})} \\ = \eta e_h x_i^k$$

注意，上面两步连接权值调整过程中的学习速率 $\eta$ ，可相同也可不相同

至此，连接权值调整部分的推导就算完成了，有兴趣的读者可以利用类似的方法推导其他几个参数的调整公式

---

网络过拟合

[Hornik et al., 1989]证明，只需要一个包含足够多神经元的隐含层，多层前馈网络就能以任意精度逼近任意复杂度的连接函数

正是由于其强大的表示能力，BP神经网络经常遭遇过拟合，其训练误差持续降低，但测试误差却可能上升。有两种策略常用来缓解BP网络的过拟合:

第一种策略是“早停”(early stopping): 将数据分成训练集和验证集，训练集用来计算梯度、更新连接权值和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值；

第二种策略是“正则化”(regularization)，其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和。任令 $E_k$表示第 $k$个训练样例上的误差，$w_i$表示连接权和阈值，则误差目标函数改变为

$$E = \lambda \frac{1}{m} \sum_{k=1}^m{E_k} + (1-\lambda) \sum_i{w_i^2}$$ 其中 $\lambda \in (0,1)$用于对经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计.

---

基本BP算法的缺陷与改进

BP算法因其简单、易行、计算量小、并行强等优点，目前是神经网络训练采用最多也是最成熟的训练算法之一

算法的缺陷

其算法的实质是求解误差函数的最小值问题，由于它采用非线性规划中的最速下降法，按误差函数的负梯度方向修改权值，且神经元之间采用全连接的方式，因而通常存在以下问题:

• 学习效率低，收敛速度慢
• 易陷入局部极小状态
  

  ---

算法的改进

附加动量

附加动量法使网络在修正其权值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响。在没有附加动量的作用下，网络可能陷入浅的局部极小值，利用附加动量就有可能滑过这些极小值。

该方法是在反向传播法的基础上再每一个权值(或阈值)的变化上加上一项比与前次权值变化量的值，并根据反向传播法来产生新的权值变化。

带有附加动量因子的权值和阈值调节公式为:

$$\Delta w_{ij}(k+1) = (1-m_c)\eta \delta_i p_j + m_c \Delta w_{ij}(k) \\ \Delta b_i(k+1) = (1-m_c)\eta \delta_i + m_c \Delta b_i(k)$$ 其中 $k$为训练次数，$m_c$为动量因子，一般取0.95左右.

附加动量法的实质是将最后一次权值变化的影响，通过一个动量因子来传递。当动量因子取值为 0 时，权值的变化仅是更加梯度下降法产生；当动量因子取值为 1 时，新的权值变化则是设置为最后一次权值的变化，而依梯度法产生的变化部分则被忽略掉了

以此方式，当增加了动量项后，促使权值的调节向着误差曲面底部的平均方向变化，当网络权值进入误差曲面底部的平坦区时，$\delta_i$将变得很小，于是 $\Delta w_{ij}(k+1) = \Delta w_{ij}(k)$，从而防止了 $\Delta w_{ij} = 0$的出现，有助于使网络从误差曲面的局部极小值中跳出

---

自适应学习速率

对于一个特定的问题，要选择适当的学习速率不是一件容易的事情。通常是凭经验或实验获取，但即使这样，对训练开始初期功效较好的学习速率，不见得对后来的训练合适。为了解决这个问题，人们自然想到在训练过程中，自动调节学习速率。

调节学习速率的准则是: 检查权值是否真正降低了误差函数，如果确实如此，则说明所选学习速率小了，可以适当增加一个量；若不是这样，而产生了过调，那么就应该减少学习速率的值。

自适应学习速率的调整公式:

$$\eta(k+1) = \begin{cases} 1.05 \eta(k), & E(k+1) < E(k) \\ 0.7 \eta(k), & E(k+1) > 1.04 E(k+1) > 1.04 E(k) \\ \eta(k), & 其它 \end{cases}$$ 其中$E(k)$为第$k$步误差平方和，初始学习速率$\eta(0)$的选取范围可以有很大的随意性。

---

动量-自适应学习速率调整算法

当采用前述的动量法时，BP算法可以找到全局最优解，而当采用自适应学习速率时，BP算法可以缩短训练时间，采用这两种方法也可以用来训练神经网络

---

设计神经网络

网络的层数

理论上已证明: 具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理数。

增加层数可以更进一步的降低误差，提高精度，但同时也使网络复杂化，从而增加了网络权值的训练时间。

而误差精度的提高实际上也可以通过增加神经元数目来获得，其训练效果也比增加层数更容易观察和调整。

所以一般情况下，应优先考虑隐含层中的神经元数

---

隐含层的神经元数

如何设置隐含层神经元的个数任是一个未决问题，实际应用中通常靠“试错法”(trial-by-error)或者经验公式来调整。

比如

$$m = \sqrt{n+l} + \alpha \\ m = log_2(n) \\ m = \sqrt{n \times l}$$ 等等一些经验公式，其中 $m$为隐含层节点数，$n$为输入层节点数，$l$为输出层节点数，$\alpha$为 1~10 之间的常数.

---

初始权值的选取

由于系统是非线性的，初始值对于学习是否达到局部最小、是否能够收敛及训练时间的长短关系很大。

如果初始值太大，使得加权后的输入和$n$落在了 S 型激活函数的饱和区，从而导致其导数 $f'(n)$非常小，而在计算权值修正公式中，因为 $\delta \infty f'(n)$，当$f'(n) \rightarrow 0$时，则有$\delta \rightarrow 0$。这使得$\Delta w_{ij} \rightarrow 0$，从而使得调节过程几乎停顿下来。所以一般总是希望经过初始加权后的每个神经元的输出值都接近于零，这样可以保证每个神经元的权值都能够在它们的 S型 激活函数变化最大之处进行调节。

所以，一般取初始值在$(-1,1)$之间的随机数.

或者可以先选取小量样本集进行BP神经网络的训练，将训练的结果作为全量样本训练神经网络的初值，可加快网络收敛速度，减少迭代次数.

---

学习速率

一般情况下，倾向于选取较小的学习速率以保证系统的稳定性，学习速率一般在 0.01~0.8 之间选取。

也可参考自适应学习速率法进行设置.

---

R语言实现BP神经网络实例

library(AMORE)  #加载神经网络工具包

#构造数据
x1 <- round(runif(2000,1,2000))
x2 <- round(runif(2000,1,2000))
#标准化训练集
x11 <- scale(x1[1:1900])
x12 <- scale(x2[1:1900])
#标准化验证集
x21 <- scale(x1[1901:2000])
x22 <- scale(x2[1901:2000])
#构造目标值
y1 <- x11^2 + x12^2
y2 <- x21^2 + x22^2

p <- cbind(x11, x12)
q <- cbind(x21, x22)
target = y1

#设计BP神经网络
net <- newff(n.neurons = c(2,5,1), learning.rate.global = 1e-2,momentum.global = 0.4,error.criterium = "LMS",Stao = NA, hidden.layer = "tansig",output.layer = "purelin",method = "ADAPTgdwm")

#训练神经网络
result <- train(net, p, target, error.criterium = "LMS", report = TRUE, show.step = 200, n.shows = 10)

#展示结果
z <- sim(result$net, q)
plot(q[1:100,1],z, col= "blue", pch = "+")
points(q[1:100,1],y2, col = "red", pch = "x")

训练结果如下图所示:

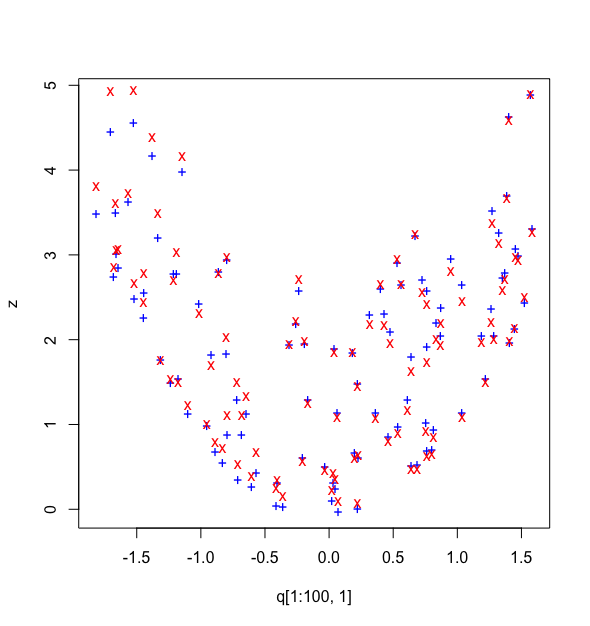
这里重点讲下newff()函数和train()函数，可通过help()函数查看函数详情

newff()函数可返还一个神经网络对象，它的参数介绍如下:
n.neurons参数是一个向量，向量的第一个元素表示输入层神经元数，最后一个元素表示输出层神经元数，中间的元素个数表示隐含层的层数，每个元素的值表示对于隐含层的神经元数，如上例中n.neurons = c(2,5,1)表示输入层有2个神经元，只有一个隐含层，隐含层的神经元数为5，输出层只有一个神经元；

learning.rate.global参数表示每个神经元学习速率

momentum.globa参数表示每个神经元的动量因子

error.criterium参数表示误差函数，目前可选"LMS":最小均方误差，"LMLS":最小对数均方误差，"TAO":TAO Error

hidden.layer参数表示隐含层神经元的激活函数，目前可选"purelin","tansig","sigmoid","hardlim","custom": 用户自定义函数

output.layer参数表示输出层的激活函数

method参数表示适合的学习方法

---

train()函数用来训练神经网络，得到各个参数的结果，它的参数介绍如下:
net表示用来训练的神经网络对象

P表示训练集

T表示目标向量

error.criterium表示评估训练结果的好坏

n.shows表示要显示迭代结果的迭代步数

show.step表示训练的最大迭代次数