@evilking 2018-05-01T14:52:40.000000Z 字数 11916 阅读 2606

时间序列篇

AR模型

定义

具有如下结构的模型称为 $p$ 阶自回归模型，简记为 $AR(p)$ :

$\begin{cases} x_t = \phi_0 + \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t \\ \phi_p \neq 0 \\ E(\epsilon_t) = 0,Var(\epsilon_t) = \sigma_{\epsilon}^2 , E(\epsilon_t \epsilon_s) = 0, s \neq t \\ E(x_s \epsilon_t) = 0, \forall s < t \end{cases}$

$AR(p)$ 模型有三个限制条件:
条件一: $\phi_p \neq 0$ . 这个限制条件保证了模型的最高阶数为 $p$ .

条件二: $E(\epsilon_t) = 0, Var(\epsilon_t) = \sigma_{\epsilon}^2 , E(\epsilon_t \epsilon_s) = 0, s \neq t$ .这个限制条件实际上是要求随机干扰序列 $\{\epsilon_t\}$ 为零均值白噪声序列.

条件三: $E(x_s \epsilon_t) = 0, \forall s < t$ . 这个限制条件说明当期的随机干扰与过去的序列值无关.

通常会缺省默认的限制条件，把 $AR(p)$ 模型简记为:

$x_t = \phi_0 + \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t$

当 $\phi_0 = 0$ 时，自回归模型又称为中心化 $AR(p)$ 模型.

非中心化 $AR(p)$ 序列都可以通过下面的变化转化为中心化 $AR(p)$ 序列.令

$\mu = \frac{\phi_0}{1-\phi_1-\cdots-\phi_p}, y_t = x_t - \mu$ 则

$\{y_t\}$ 为

$\{x_t\}$ 的中心化序列.中心化变换实际上就是非中心化序列整体平移了一个常数位移，这种整体移动对序列值之间的相关关系没有任何影响.

引进延迟算子，中心化 $AR(p)$ 模型又可以简记为:

$\Phi(B) x_t = \epsilon_t$ 式中，

$\Phi(B) = 1-\phi_1 B - \phi_2 B^2 - \cdots - \phi_p B^p$ ，称为

$p$ 阶自回归系数多项式.

$AR$ 模型平稳性判别

特征根判别

任一中心化 $AR(p)$ 模型 $\Phi(B) x_t = \epsilon_t$ 都可以被视为一个非齐次线性差分方程:

$x_t - \phi_1 x_{t-1} - \phi_2 x_{t-2} - \cdots - \phi_p x_{t-p} = \epsilon_t$ 方程的通解为:

$x_t = x_t' + x_t''$ 式中，

$x_t'$ 为齐次线性差分方程

$\Phi(B)x_t = 0$ 的通解；

$x_t''$ 为上述非齐次线性差分方程的一个特解.

求齐次线性差分方程 $\Phi(B) x_t = 0$ 的一个通解 $x_t'$ . 假定 $\lambda_1, \lambda_2, \cdots, \lambda_p$ 是该特征方程的 $p$ 个特征根.为了有代表性，不妨假设这 $p$ 个特征根取值如下:
$\lambda_1 = \lambda_2 = \cdots = \lambda_d$ 为 $d$ 个相等实根.
$\lambda_{d+1},\lambda_{d+2},\cdots,\lambda_{p-2m}$ 为 $p-d-2m$ 个互不相等的实根.
$\lambda_{j1} = r_je^{i\omega_j},\lambda_{j2} = r_j e^{-i\omega_j} ,j = 1,\cdots,m$ 为 $m$ 对共轭复根.
那么齐次线性差分方程 $\Phi(B) x_t = 0$ 的通解为:
$x_t' = \sum_{j=1}^d{c_j t^{j-1} \lambda_1^t} + \sum_{j=d+1}^{p-2m}{c_j \lambda_j^t} + \sum_{j=1}^m{r_j^t(c_{1j}e^{it\omega_j} +c_{2j}e^{-it\omega_j})}$ 式中， $c_1,\cdots,c_{p-2m},c_{1j},c_{2j} \ \ ,j=1,\cdots,m$ 为任意实数.
求非齐次线性差分方程 $\Phi(B) x_t = 0$ 的一个特解 $x_t''$ . 首先，可以证明 $AR(p)$ 模型的自回归系数多项式 $\Phi(\mu) = 0$ 的根是齐次线性差分方程 $\Phi(B) x_t = 0$ 的特征根的倒数.
证明: 设 $\lambda_1, \lambda_2, \cdots, \lambda_p$ 为齐次线性差分方程 $\Phi(B)x_t = 0$ 的 $p$ 个特征根，任取 $\lambda_i , i \in (1,2,\cdots,p)$ 带入特征方程，有
$\lambda_i^p - \phi_1 \lambda_i^{p-1} - \phi_2 \lambda_i^{p-2} - \cdots - \phi_p = 0$ 把 $\mu_i = \frac{1}{\lambda_i}$ 带入 $AR(p)$ 模型的自回归系数多项式中，有
$\Phi(\mu_i) = 1 - \phi_1 \frac{1}{\lambda_i} - \cdots - \phi_p \frac{1}{\lambda_i^p} \\ = \frac{1}{\lambda_i^p}\left[ \lambda_i^p - \phi_1 \lambda_i^{p-1} - \cdots - \phi_p \right] = 0$

根据这个性质， $\Phi(B)$ 可以因子分解成
$\Phi(B) = \prod_{i=1}^p{(1-\lambda_i B)}$ 由此可以得到非齐次线性差分方程的一个特解为:
$x_t'' = \frac{\epsilon_t}{\Phi(B)} = \frac{\epsilon_t}{\prod_{i=1}^p {(1-\lambda_i B)}} = \sum_{i=1}^p{\frac{k_i}{1-\lambda_i B}}\epsilon_t$ 式中， $k_i (i = 1,2,\cdots,p)$ 为常数.
求非齐次线性差分方程的通解 $x_t$

$x_t = x_t' + x_t'' \\ = \sum_{j=1}^d{c_j t^{j-1} \lambda_1^t} + \sum_{j=d+1}^{p-2m}{c_j \lambda_j^t} + \sum_{j=1}^m{r_j^t(c_{1j}e^{it\omega_j} +c_{2j}e^{-it\omega_j})} \\ + \sum_{i=1}^p{\frac{k_i}{1-\lambda_i B}}\epsilon_t$

要使得中心化 $AR(p)$ 模型平稳，即要求对任意实数 $c_1,\cdots, c_{p-2m}, c_{1j},c_{2j},\ \ \ j = 1,2,\cdots,m$ ，有

$\lim_{t \rightarrow +\infty} x_t = 0$ 要使该式子成立的充要条件是

$|\lambda_i| < 1, i = 1,2,\cdots,p-2m \\ |r_i| < 1, i = 1,2,\cdots,m\ \ \ \ \ \ \ \ \ \$ 实际上就是要求

$AR(p)$ 模型的

$p$ 个特征根都在单位圆内.所以

$AR(p)$ 模型平稳的充要条件是它的

$p$ 个特征根都在单位圆内.

根据特征根和自回归系数多项式的根成倒数的关系，AR模型平稳的等价判别条件是该 AR 模型的自回归系数多项式的根，即 $\Phi(\mu) = 0$ 的根，都在单位圆外.

平稳域判别

对于一个 $AR(p)$ 模型而言，如果没有平稳性的要求，实际上也就意味着对参数向量 $(\phi_1,\phi_2,\cdots,\phi_p)'$ 没有任何限制，它们可以取遍 $p$ 维欧式空间中的任意一点，但是如果加上平稳性限制，参数向量 $(\phi_1,\phi_2,\cdots,\phi_p)'$ 就只能取 $p$ 维欧式空间的一个子集，使得特征根都在单位圆内的系数集合

特 征 根 都 在 单 位 圆 内

$\{\phi_1,\phi_2,\cdots,\phi_p|特征根都在单位圆内\}$ 称为

$AR(p)$ 模型的平稳域.

下面以低阶 $AR$ 模型用平稳域的方法判别模型的平稳性为例来说明:

$AR(1)$ 模型的平稳域
$AR(1)$ 模型为: $x_t = \phi_1 x_{t-1} + \epsilon_t$ ，其特征方程为: $\lambda - \phi_1 = 0$ ，特征根为: $\lambda = \phi_1$ ，根据 $AR$ 模型平稳的充要条件，容易推出 $AR(1)$ 模型平稳的充要条件是
$|\phi_1| < 1$ 所以， $AR(1)$ 模型的平稳域就是: $\{\phi_1 | -1 < \phi_1 < 1\}$ .
$AR(2)$ 模型的平稳域
$AR(2)$ 模型为: $x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \epsilon_t$ ，其特征方程为: $\lambda^2 - \phi_1 \lambda - \phi_2 = 0$ ，特征根为: $\lambda_1 = \frac{\phi_1 + \sqrt{\phi_1^2 + 4 \phi_2}}{2}, \lambda_2 = \frac{\phi_1 - \sqrt{\phi_1^2 + 4 \phi_2}}{2}$ 根据 $AR$ 模型的平稳的充要条件， $AR(2)$ 模型平稳的充要条件是 $|\lambda_1|<1, |lambda_2|<1$

根据一元二次方程的性质和 $AR(2)$ 模型的平稳条件，有
$且$
可以导出:
1. $|\phi_2| = |\lambda_1\lambda_2| < 1$
2. $\phi_2 + \phi_1 = -\lambda_1 \lambda_2 + \lambda_1 + \lambda_2 = 1 - (1 - \lambda_1)(1-\lambda_2) < 1$
3. $\phi_2 - \phi_1 = -\lambda_1 \lambda_2 - \lambda_1 - \lambda_2 = 1 - (1+\lambda_1)(1+\lambda_2) < 1$
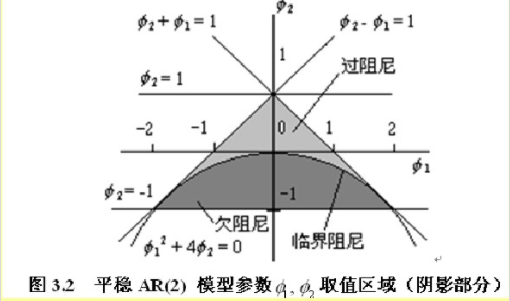
这三个限制条件意味着 $AR(2)$ 模型的平稳域是一个三角形区域， $\{\phi_1, \phi_2| |\phi_2| < 1, 且 \phi_2 \overline{+} \phi_1 < 1\}$

ar1

平稳 $AR$ 模型的统计性质

均值

假如 $AR(p)$ 模型满足了平稳性条件，在等式两边取期望，得

$E(x_t) = E(\phi_0 + \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t)$ 根据平稳序列均值为常数的性质，有

$E(x_t) = \mu \ \ \ \ (\forall t \in T)$ ，且因为

$\{\epsilon_t\}$ 为白噪声序列，有

$E(\epsilon_t) = 0$ ，所以有

$(1 - \phi_1 - \cdots - \phi_p) \mu = \phi_0$ 求得:

$\mu = \frac{\phi_0}{1-\phi_1 - \cdots - \phi_p}$ 特别地，对于中心化

$AR(p)$ 模型，有

$E(x_t) = 0$

方差

Green函数

设 $\lambda_1,\lambda_2,\cdots,\lambda_p$ 为平稳 $AR(p)$ 模型的特征根，则平稳 $AR(p)$ 模型可以写成如下形式:

$x_t = \frac{\epsilon_t}{\Phi(B)} \\ = \sum_{i=1}^p{\frac{k_i}{1-\lambda_i B} \epsilon_t} \\ = \sum_{i=1}^p{\sum_{j=0}^{\infty}{k_i(\lambda_i B)^j \epsilon_t}} \\ = \sum_{j=0}^{\infty}{\sum_{i=1}^p{k_i \lambda_i^j \epsilon_{t-j}}} \\ \hat{=} \sum_{j=0}^{\infty}{G_j \epsilon_{t-j}}$ 式中，

$G_0 = 1, G_j = \sum_{i=1}^p{k_i \lambda_i^j},\ \ j = 1,2,\cdots$

上式称为 $AR$ 模型的传递形式，系数 $G_j ,j = 0,1,2,\cdots$ 称为 $Green$ 函数.因为 $\lambda_1,\lambda_2,\cdots,\lambda_p$ 都在单位圆内，所以 $Green$ 函数应该呈指数下降，且 $\lim_{j \rightarrow +\infty} |G_j| = 0$ 通过待定系数法，可以确定 $Green$ 函数的递推公式.

记 $G(B) = \sum_{j=0}^{\infty} {G_j B^j}$ ，则中心化 $AR(p)$ 模型可以简记为:

$x_t = G(B) \epsilon_t$ 把上式带入

$AR(p)$ 模型

$\Phi(B) = \epsilon_t$ ，得到

$\Phi(B) G(B) \epsilon_t = \epsilon_t$ 展开上式，得

$\left( 1- \sum_{k=1}^p{\phi_k B^k} \right) \left( \sum_{j=0}^p{G_j B^j} \right) \epsilon_t = \epsilon_t$ 整理得:

$\left[ 1 + \sum_{j=1}^{\infty} \left( G_j - \sum_{k=1}^j{\phi_k' G_{j-k}} \right) B^j \right] \epsilon_t = \epsilon_t$ 根据待定系数法，有

$G_j - \sum_{k=1}^j{\phi_k' G_{j-k}} = 0, \ \ j = 1,2,\cdots$ 由此可以得到

$Green$ 函数递推公式:

$\begin{cases} G_0 = 1 \\ G_j = \sum_{k=1}^j {\phi_k' G_{j-k}} , \ \ j=1,2,\cdots \end{cases}$ 式中

$\phi_k' = \begin{cases} \phi_k, \ \ k \leq p \\ 0, \ \ k > p \end{cases}$

平稳 $AR$ 模型的方差

对平稳 $AR$ 模型等式两边求方差，有

$Var(x_t) = \sum_{j=0}^{\infty}{G_j^2 Var(\epsilon_t)}$ 式中，

$\{\epsilon_t\}$ 为白噪声序列；

$Var(\epsilon_t) = \sigma_{\epsilon}^2$ ，所以

$Var(x_t) = \sum_{j=0}^{\infty} {G_j^2 \sigma_{\epsilon}^2}$ 因为

$G_j$ 呈指数下降，所以

$\sum_{j=0}^{\infty} G_j^2 < \infty$ ，这说明平稳序列

$\{x_t\}$ 方差有界，等于常数

$\sum_{j=0}^{\infty}{G_j^2 \sigma_{\epsilon^2}}$

协方差函数

在平稳模型 $x_t= \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t$ 等号两边同乘 $x_{t-k}, \forall k \geq 1$ ，再求期望，得

$E(x_t x_{t-k}) = \phi_1 E(x_{t-1} x_{t-k}) + \cdots + \phi_p E(x_{t-p} x_{t-k}) + E(\epsilon_t x_{t-k}), \forall k \geq 1$ 因为

$E(\epsilon_t x_{t-k}) = 0, \forall k \geq 1$ ，于是可以得到如下自协方差函数的递推方式:

$\gamma_k = \phi_1 \gamma_{k-1} + \phi_2 \gamma_{k-2} + \cdots + \phi_p \gamma_{k-p}$

自相关系数

平稳 $AR$ 模型自相关系数递推公式

由于 $\rho_k = \frac{\gamma_k}{\gamma_0}$ ，在自协方差函数的递推公式等号两边同除以方差函数 $\rho_0$ ，就得到自相关系数的递推公式:

$\rho_k = \phi_1 \rho_{k-1} + \phi_2 \rho_{k-2} + \cdots + \phi_p \rho_{k-p}$ 容易验证平稳

$AR(1)$ 模型的自相关系数递推公式为:

$\rho_k = \phi_1^k$ 平稳

$AR(2)$ 模型的自相关系数递推公式为:

$\rho_k = \begin{cases} 1, \ \ \ \ k = 0 \\ \frac{\phi_1}{1-\phi_2}, \ \ k = 1 \\ \phi_1 \rho_{k-1} + \phi_2 \rho_{k-2}, k \geq 2 \end{cases}$

自相关系数的性质

平稳 $AR(p)$ 模型的自相关系数有两个显著的性质:
1. 一是拖尾性；
2. 二是呈指数衰减.

根据自相关系数的递推公式， $AR(p)$ 模型的自相关系数的表达式实际上是一个 $p$ 阶齐次差分方程.那么滞后任意 $k$ 阶的自相关系数的通解为:

$\rho_k = \sum_{i=1}^p{c_i \lambda_i^k}$ 式中，

$|\lambda_i| < 1, i = 1,2,\cdots,p$ 为该差分方程的特征根；

$c_1,c_2,\cdots,c_p$ 为任意常数，如果已知任意

$p$ 个自相关系数的值就可以确定

$c_1,c_2,\cdots, c_p$ 的解，显然

$c_1,c_2,\cdots,c_p$ 不能全为零.

通过这个通解形式，容易推出 $\rho_k$ 始终有非零取值，不会在 $k$ 大于某个常数之后就恒等于零，这个性质就是拖尾性.

可以直观的解释 $AR(p)$ 模型自相关系数拖尾的原因.对于一个平稳 $AR(p)$ 模型:

$x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t$ 虽然他的表达式显示

$x_t$ 只受当期随机误差

$\epsilon_t$ 和最近

$p$ 期序列值

$x_{t-1} ,\cdots,x_{t-p}$ 的影响，但是由于

$x_{t-1}$ 的值又依赖于

$x_{t-1-p}$ ，所以实际上

$x_{t-1-p}$ 对

$x_t$ 也有影响，依次类推，

$x_t$ 之前的每一个序列值

$x_{t-1},\cdots,x_{t-k},\cdots$ 都会对

$x_t$ 构成影响.自回归模型的这种特性体现在自相关系数上就是自相关系数的拖尾性.

同时随着时间的推移， $\rho_k$ 会迅速衰减，因为 $|\lambda_i| < 1, i = 1,2,\cdots,p$ ，所以 $k \rightarrow \infty$ 时， $\lambda_i^k \rightarrow 0 , i = 1,2,\cdots, p$ ，继而导致 $\rho_k = \sum_{i=1}^p{c_i \lambda_i^k} \rightarrow 0$ ，而且这种影响是以指数 $\lambda^k$ 的速度在衰减.

这种特性表明对平稳序列而言，通常只有近期的序列值对现时值的影响比较明显，间隔越远的过去值对现时值的影响越小.

偏自相关系数

偏自相关系数的定义

对于一个平稳 $AR(p)$ 模型，求出滞后 $k$ 自相关系数 $\rho_k$ 时，实际上得到的并不是 $x_t$ 与 $x_{t-k}$ 之间单纯的相关关系.因为 $x_t$ 同时还会受到中间 $k-1$ 个随机变量 $x_{t-1},x_{t-2},\cdots,x_{t-k+1}$ 的影响，而这 $k-1$ 个随机变量又都和 $x_{t-k}$ 具有相关关系，所以自相关系数 $\rho_k$ 里实际上掺杂了其他变量对 $x_t$ 与 $x_{t-k}$ 的相关影响.为了能单纯的测度 $x_t$ 与 $x_{t-k}$ 的影响，引进偏自相关系数的概念.

对于平稳序列 $\{x_t\}$ ，所谓滞后 $k$ 偏自相关系数，就是指在给定中间 $k-1$ 个随机变量 $x_{t-1},x_{t-2},\cdots,x_{t-k+1}$ 的条件下，或者说，在剔除了中间 $k-1$ 个随机变量 $x_{t-1},x_{t-2},\cdots,x_{t-k+1}$ 的干扰之后， $x_{t-k}$ 对 $x_t$ 相关影响的度量.

公式化描述为

$\rho_{x_t,x_{t-k}|x_{t-1},\cdots,x_{t-k+1}} = \frac{E[(x_t - \hat{E}(x_t))(x_{t-k} - \hat{E}(x_{t-k}))]}{E[(x_{t-k} - \hat{E}(x_{t-k}))^2]}$ 式中，

$\hat{E}(x_t) = E[x_t | x_{t-1},\cdots,x_{t-k+1}], \hat{E}(x_{t-k}) = E[x_{t-k} | x_{t-1},\cdots,x_{t-k+1}]$ ，这就是滞后

$k$ 偏自相关系数的定义.

偏自相关系数的计算

假定 $\{x_t\}$ 为中心化平稳序列，用过去的 $k$ 期序列值 $x_{t-1},x_{t-2},\cdots,x_{t-k}$ 对 $x_t$ 作 $k$ 阶自回归拟合，即

$x_t = \phi_{k1} x_{t-1} + \phi_{k2} x_{t-2} + \cdots + \phi_{kk} x_{t-k} + \epsilon_t$ 式中，

$E(\epsilon_t) = 0, E(\epsilon_t x_s) = 0, \forall s < t$ ，对

$x_{t-1},x_{t-2},\cdots,x_{t-k+1}$ 取条件期望，记

，

$\hat{E(x_t)} = E[x_t | x_{t-1},\cdots,x_{t-k+1}]，\hat{E}(x_{t-k}) = E[x_{t-k} | x_{t-1},\cdots,x_{t-k+1}]$ 则

$\hat{E}(x_t) = \phi_{k1} x_{t-1} + \phi_{k2} x_{t-2} + \cdots + \phi_{k(k-1)} x_{t-k+1} + \phi_{kk} \hat{E}(x_{t-k}) + E(\epsilon_t | x_{t-1},\cdots,x_{t-k+1})$ 已知

$E(\epsilon_t) = 0, E(\epsilon_t x_s) = 0, \forall s < t$ ，所以

$E(\epsilon_t | x_{t-1},\cdots,x_{t-k+1}) = E(\epsilon_t) = 0$ 则有

$\hat{E}(x_t) = \phi_{k1} x_{t-1} + \phi_{k2} x_{t-2} + \cdots + \phi_{k(k-1)} x_{t-k+1} + \phi_{kk} \hat{E}(x_{t-k})$ 那么

$x_t - \hat{E}(x_t) = \phi_{kk} (x_{t-k} - \hat{E}(x_{t-k})) + \epsilon_t$ 在等式两边同时乘以

$x_{t-k} - \hat{E}(x_{t-k})$ ，并求期望:

$E[(x_t - \hat{E}(x_t)(x_{t-k} - \hat{E}(x_{t-k})))] = \phi_{kk} E[(x_{t-k} - \hat{E}(x_{t-k}))^2] + E[\epsilon_t (x_{t-k} - \hat{E}(x_{t-k}))]$ 因为

$E(\epsilon_t x_s) = 0, \forall s < t$ ，所以

$E[\epsilon_t (x_{t-k} - \hat{E}(x_{t-k}))] = 0$ 所以上式等于

$E[(x_t - \hat{E}(x_t)(x_{t-k} - \hat{E}(x_{t-k})))] = \phi_{kk} E[(x_{t-k} - \hat{E}(x_{t-k}))^2]$ 由此得出

$\phi_{kk} = \frac{E[(x_t - \hat{E}(x_t))(x_{t-k} - \hat{E}(x_{t-k}))]}{E[(x_{t-k} - \hat{E}(x_{t-k}))^2]}$ 等号右边的结果正好等于滞后

$k$ 偏自相关系数的定义式.

这说明滞后 $k$ 偏自相关系数实际上就等于 $k$ 阶自回归模型第 $k$ 个回归系数 $\phi_{kk}$ 的值，根据这个性质就容易计算偏自相关系数的值.

在对 $x_t$ 做 $k$ 阶自回归拟合方程中，两边同时乘以 $x_{t-l}$ ，并求期望，得

$\rho_l = \phi_{k1} \rho_{l-1} + \phi_{k2} \rho_{l-2} + \cdots + \phi_{kk} \rho_{l-k} , \forall l \geq 1$ 取前

$k$ 个方程构成的方程组:

$\begin{cases} \rho_1 = \phi_{k1} \rho_0 + \phi_{k2} \rho_1 + \cdots + \phi_{kk} \rho_{k-1} \\ \rho_2 = \phi_{k1} \rho_1 + \phi_{k2} \rho_0 + \cdots + \phi_{kk} \rho_{k-2} \\ \ \ \ \ \vdots \\ \rho_k = \phi_{k1} \rho_{k-1} + \phi_{k2} \rho_{k-2} + \cdots + \phi_{kk} \rho_0 \end{cases}$ 该方程组称为

$Yule-Walker$ 方程.通过解该方程组，可以得到参数

$(\phi_{k1},\phi_{k2},\cdots,\phi_{kk})'$ 的解，参数向量中最后一个参数的解，即为滞后

$k$ 偏自相关系数

$\phi_{kk}$ 的值.

用矩阵形式表示为:

$\left[ \begin{matrix} 1 & \rho_1 & \cdots & \rho_{k-1} \\ \rho_1 & 1 & \cdots & \rho_{k-2} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \phi_{k1} \\ \phi_{k2} \\ \vdots \\ \phi_{kk} \end{matrix} \right] = \left[ \begin{matrix} \rho_1 \\ \rho_2 \\ \vdots \\ \rho_k \end{matrix} \right]$
根据线性方程组求解的

$Crammer$ 法则，有

$\phi_{kk} = \frac{D_k}{D}$ 式中

$D = \left| \begin{matrix} 1 & \rho_1 & \cdots & \rho_{k-1} \\ \rho_1 & 1 & \cdots & \rho_{k-2} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots & 1 \\ \end{matrix} \right|, \\ D_k = \left| \begin{matrix} 1 & \rho_1 & \cdots & \rho_1 \\ \rho_1 & 1 & \cdots & \rho_2 \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots & \rho_k \\ \end{matrix} \right|$

$D$ 为矩阵形式中系数矩阵的行列式，

$D_k$ 是把

$D$ 中的第

$k$ 个列向量换成矩阵形式中等号右边的自相关系数向量后构成的矩阵行列式.

偏自相关系数的截尾性

可以证明: 平稳 $AR(p)$ 模型的偏自相关系数具有 $p$ 步截尾性.所谓 $p$ 步截尾是指， $\phi_{kk} = 0, \forall k > p$ 要证明这一点实际上只要证明当 $k > p$ 时， $D_k= 0$ 即可.

证明:

对任一 $AR(p)$ 模型

$x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t, \forall k > p$ 有如下

$Yule-Walker$ 方程成立:

$\boldsymbol{\xi}_i , i = 1,2,\cdots,p$ 为系数矩阵中

$p$ 个列向量，

$\boldsymbol{\eta}$ 为式中等号右边的自相关系数向量，即

$\boldsymbol{\xi}_i = \left[\begin{matrix} \rho_{i-1} \\ \rho_{i-2} \\ \vdots \\ \rho_{k-i} \end{matrix} \right] , i = 1,2,\cdots,p; \boldsymbol{\eta} = \left[\begin{matrix} \rho_1 \\ \rho_2 \\ \vdots \\ \rho_k \end{matrix} \right]$ 则有

$\boldsymbol{\eta} = \phi_1 \boldsymbol{\xi}_1 + \phi_2 \boldsymbol{\xi}_2 + \cdots + \phi_p \boldsymbol{\xi}_p$ 因为

$AR(p)$ 模型限制条件之一是

$\phi_p \neq 0$ ，所以向量

$\boldsymbol{\eta}$ 一定可以表示成向量

$\boldsymbol{\xi}_i , i = 1,2,\cdots,p$ 的非零线性组合.

当 $k > p$ 时

$D_k = \left| \begin{matrix} 1 & \rho_1 & \cdots & \rho_{p-1} & \cdots & \rho_1 \\ \rho_1 & 1 & \cdots & \rho_{p-2} & \cdots & \rho_2 \\ \vdots & \vdots & & \vdots & & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots & \rho_{k-p} & \cdots & \rho_k \\ \end{matrix} \right|$ 显然

$D_k$ 的前

$p$ 个列向量正好就是

$\boldsymbol{\xi}_i , i = 1,2,\cdots,p$ ，而最后一个列向量正好就是向量

$\boldsymbol{\eta}$ ，根据计算公式，说明在行列式中最后一个列向量可以用另外

$p$ 个列向量的线性组合表示.根据行列式的性质，具有这种线性相关关系的行列式的值一定为零，即

$D_k = 0$ .由

$D_k = 0$ 等级推出

$\phi_{kk} = 0$ .

证毕.

由此证明了 $AR(p)$ 模型偏自相关系数的 $p$ 步截尾性.这个性质连同前面的自相关系数拖尾性是 $AR(p)$ 模型识别的重要依据.

AR模型

定义

AR模型平稳性判别