NLP

基于深度学习的情感分析

网上有说基于SVM的情感分析的，有基于深度学习的情感分析的等等，其实大部分都是用某种编码器将文档编码成向量，然后用向量拿去做分类，分成正面、负面、或中性。

其中有用 doc2vec 将文本转换成向量后，再用 SVM
做分类的；有用 CNN 或者 LSTM 将文本转换成向量，再拿去分类的。核心是将文本转换成向量时，要使向量包含并突出情感信息，这样拿去分类时效果才好。

本文主要是将用 递归自编码器(Recursive AutoEncoder,RAE) 将文档转换成向量，然后再模型中追加一层输出分类层，用于情感分类。

---

自编码器

在讲递归自编码前，先讲下自编码器。

Auto-Encoder（AE）是 20 世纪 80 年代提出的，基本的 AE 可视为一个三层神经网络结构：一个输入层、一个隐藏层和一个输出层，其中输出层与输入层具有相同的规模；它是一种无监督学习算法，使用了反向传播，让目标值尽可能等于输入值。如图：

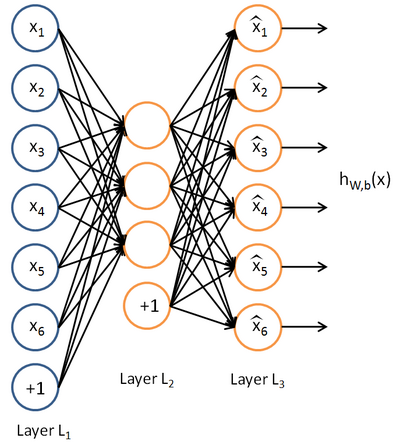
其中 $\mathbf{x} = (x_1,x_2,\cdots,x_6)$ 为输入向量，$\mathbf{\hat{x}} = (\hat{x}_1,\hat{x}_2,\cdots,\hat{x}_6)$ 为输出向量，中间隐藏层的向量为 $\mathbf{h} = (h_1,h_2,\cdots,h_k)$，$k$ 为隐藏层神经元数.

自编码器分为两部分： 编码器 (encoder)和 解码器 (decoder). 从输入层到隐藏层是编码过程，从隐藏层到输出层是解码过程. 设 $f,g$ 分别表示编码函数和解码函数，则两个过程可写为:

$$\mathbf{h} = f(\mathbf{x}) := s_f(\mathbf{W} \mathbf{x} + \mathbf{p}) \\ \mathbf{\hat{x}} = g(\mathbf{h}) := s_g(\mathbf{\hat{W}} \mathbf{h} + \mathbf{q})$$

自编码器的目的是学习出参数 $\theta = \{ \mathbf{W},\mathbf{\hat{W}},\mathbf{p},\mathbf{q} \}$ ，要尽量使 $\mathbf{x} \approx \mathbf{\hat{x}}$。

其中 $s_f$ 为编码器的激活函数，通常取 sigmoid 函数，即 $s_f(z) = \frac{1}{1 + e^{-z}}$ ；$s_g$ 为解码器的激活函数，通常取 sigmoid 函数或恒等函数，即 $s_g(z) = \frac{1}{1 + e^{-z}}$ 或 $s_g(z) = z$ .权值矩阵 $\mathbf{\hat{W}}$ 通常取为 $\mathbf{W}^T$ （虽然这不是必须的），表示解码阶段是编码阶段的逆过程；$\mathbf{p},\mathbf{q}$ 分别为两层神经网络的偏置项。

回想写 AE 的结构，先将 $\mathbf{x}$ 编码成 $\mathbf{h}$，再将 $\mathbf{h}$ 解码成 $\mathbf{\hat{x}}$，显然解码后的 $\mathbf{\hat{x}}$ 应该与编码前的 $\mathbf{x}$ 尽可能接近. 若将 AE 看成一个普通的三层神经网络，$\mathbf{\hat{x}}$ 就可以看作是 $\mathbf{x}$ 的一个预测（prediction），因此，$\mathbf{\hat{x}}$ 和 $\mathbf{x}$ 确实应该尽可能接近. 这种接近程度可以通过 重构误差 (reconstruction error)函数 $L(x,y)$ 来进行刻画.

根据解码器函数 $s_g$ 的不同，$L(x,y)$ 通常有两种取法：

1. 当 $s_g$ 为恒等函数时，取 平方误差 (squared error) 函数
   

   $$L(\mathbf{x},\mathbf{\hat{x}}) = ||\mathbf{x} - \mathbf{\hat{x}}||^2$$

2. 当 $s_g$ 为 sigmoid 函数（此时输入 $x_i \in [0,1]$）时，取 交叉熵 (cross-entropy) 函数
   

   $$L(\mathbf{x},\mathbf{\hat{x}}) = -\sum_{i=1}^n \left[ x_i \log{(\hat{x}_i)} + (1 - x_i) \log{(1 - \hat{x}_i)} \right]$$

有了重构误差函数，我们就可以针对训练数据集 $S$，提出一个整体的损失函数（loss function）

$$\cal{J}_{AE}(\theta) = \sum_{\mathbf{x} \in S} L(\mathbf{x},g(f(\mathbf{x})))$$
对这个函数进行极小化，就可以得到所需的参数 $\theta$ .

AE 最初是作为一个 降维 技巧来使用的，隐藏层上的 $\mathbf{h}$ 被视为 $\mathbf{x}$ 的一种降维表示，即 $k$ 要小于 $\mathbf{x}$ 的维度. 特别地，若进一步要求编码激活函数 $s_f$ 为 线性函数，则编码器得到的 $\mathbf{h}$ 相当于是对 $\mathbf{x}$ 做主成分分析（PCA）.

AE 还有一些变种算法，为了解决一些特定的问题，详细可参考：http://blog.csdn.net/pi9nc/article/details/27711441

---

有监督的RAE

我们了解了自编码器的原理过程，下面将结合递归神经网络和自编码器，讲解有监督的递归自编码器的原理，如何将句子递归的编码成向量.

“有监督的RAE”中的“有监督”体现在要事先知道句子的语法解析结构，如

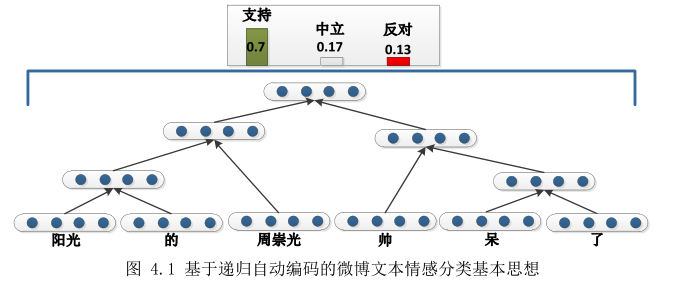
图中句子“阳光的周崇光帅呆了”，从句法解析上看，词与词之间的组合有个顺序，这个顺序需要事先知道，这就是有监督.

给定句子的各个单词的特定结构后，其实就有了一颗语法解析树，从图中可以看到根结点的向量即可表示整颗树了，也就是能表示整个句子。另外我们还需要用一个向量来表示单词，初始化时一般我们可以用 word2vec 来训练出单词的向量表示，在 RAE 训练的过程中，会更新单词向量表示，从而能捕获特定的结构信息，比如情感信息.

句子的句法解析树我们可以通过对句子进行句法分析得到，此时就可以应用有监督的 RAE 了；但这时模型就变得比较复杂，实验效果还需要依赖于句法分析的准确度.

另一种就是使用后面会讲到的无监督的 RAE ，完全根据自编码器的重构误差来做贪心递归，自动构建出这种特定结构的树.

---

下面讲解递归自编码器的思想：

例如，“深度”的词向量为 $[0.3,0.1,0.6]^T$，“学习”的词向量表示为 $[0.2,0.5,0.7]^T$ ，那么该如何表示“深度学习”呢？

假设“深度学习”是“深度”、“学习”的父节点 $p$，“深度”是左子节点 $c_1$，“学习”是右子节点 $c_2$，那么 $p$ 可以由函数 $f$ 从 $c_1,c_2$ 映射得到：

$$p = f(w^{(1)}[c_1;c_2] + b^{(1)})$$
其中 $[c_1;c_2] \in R^{2n}$，由向量 $c_1,c_2$ 联结得到；$w^{(1)} \in R^{n \times 2n}$ 是一个参数矩阵；$b^{(1)} \in R^n$ 为偏置项；编码器函数 $f(\cdot)$ 在这里选取双曲正切函数 $\tanh(\cdot)$ .

由上述公式即可得到父节点“深度学习”的向量表示，为了验证父节点对子节点 $c_1,c_2$ 的表示能力，参考自编码器的原理，可在父节点 $p$ 上建立一个重建层，重建两个子节点的表达式为:

$$[c_1';c_2'] = g(w^{(2)} p + b^{(2)})$$
其中 $c_1',c_2' \in R^n$ 是重建子节点；$w^{(2)} \in R^{n \times 2n}$ 是参数矩阵；$b^{(2)} \in R^n$ 是偏置项；解码器函数 $g(\cdot)$ 这里取恒等函数。

类似的，将自编码网络递归地应用于句子的句法解析树上的每一层，即可得到整个句子的向量表示，即根节点向量.

父节点 $p$ 为了能在下一次递归，所以父节点的维度要与输入的词向量维度相同.

另外需要注意的是，$w^{(1)},w^{(2)},b^{(1)},b^{(2)}$ 在每一层递归自编码时都是共享的，参数一样.

为了评估重建结点 $c_1',c_2'$ 与原始节点的相似度，使用重构误差函数描述，如式:

$$E_{rae} = ||c_1 - c_1'||^2 + ||c_2 - c_2'||^2$$

这种神经网络被称为递归自编码，下图展示了应用于一个二叉树的递归自编码网络，其中圆形节点表示原始节点，矩形节点表示重建节点。对二又树的每一个节点使用自编码器，那么该二叉树最终可 由一个三元组（例如，$(p_1 \rightarrow c_1c_2)$，$p$ 是父节点，$c_1、c_2$ 是子节点）集合表示。图中的二叉树可表示为: $(y_1 \rightarrow x_1 x_2),(y_2 \rightarrow y_1 x_3) 和 (y_3 \rightarrow y_2 x_4)$。

---

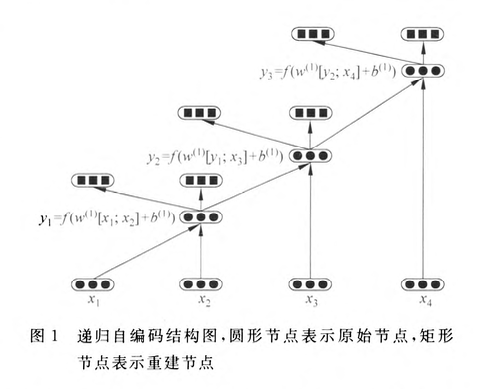
仔细分析发现，按上面的自编码方式进行训练可能出现两个问题：

1. 节点的向量表示为零向量，这会导致该节点的重建误差 $E_{rae}$ 为零，事实上，这是没有意义的；

2. 节点 $c_1,c_2$ 可能包含的叶子节点数有很大差异，计算重建误差时会导致不平衡；

为了解决问题 (1) ，可以使用单位向量来表示节点 $p$ （$p$ 表示任一节点）：

$$p = \frac{f(w^{(1)}[c_1;c_2] + b^{(1)})}{||f(w^{(1)}[c_1;c_2] + b^{(1)})||}$$
通过对父节点的向量进行正则化，可以有效避免优化算法因最小化重建误差而导致父节点向量为零向量。

为了解决问题 (2)，可以在计算重建误差 $E_{rae}$ 时，为每个子节点添加权重，权重的设定根据每个子节点所包含叶子节点数计算；假定节点 $c_1$ 的叶子节点数为 $n_1$，节点 $c_2$ 的叶子节点数为 $n_2$，重新定义重建误差 $E_{rae}$：

$$E_{rae} = \frac{n_1}{n_1 + n_2} ||c_1 - c_1'||^2 + \frac{n_2}{n_1 + n_2} ||c_2 - c_2'||^2$$

通过节点权重的添加，可以使得计算重建误差时更多地偏向子节点数目更多的节点，从而达到平衡误差的效果。

---

无监督的RAE

“无监督”是指事先不需要知道句子的语法解析结构，如果不知道树的结构了如何来做递归呢？

类似于 Haffuman 树 的构造过程，我们按一定的规则逐渐合并两个节点（这里就是两个单词的词向量），这样递归合并后就能逐渐构造出一颗特定结构的树。

那应按什么样的规则合并好呢？

我们选取 重建误差最小 的一对相邻节点来合并，并构建出其父节点替代这两个子节点。

假设一个句子包含 $m$ 个单词，即 $S = (w_1,w_2,\cdots,w_m)$，对应的词向量序列为 $C = (c_1,c_2,\cdots,c_m)$，则我们按如下操作合并：

1. 先将 $[c_1;c_2]$ 输入自编码器，保存其父节点 $p_1$ 和重建误差 $e_1$
2. 然后左移一个窗口，将 $c_2;c_3$ 输入自编码器，保存其父节点 $p_2$ 和重建误差 $e_2$
3. 依次左移，直到当前层句子的最后一对节点，将 $[c_{m-1};c_m]$ 输入自编码器，保存期父节点 $p_{m-1}$ 和 重建误差 $e_{m-1}$
4. 比较所有对的重建误差，取最小的重建误差对应的两个节点进行合并，即用父节点代替其两个子节点
5. 若第一对重建误差最小，则新一轮节点序列为 $p_1,c_3,c_4,\cdots,c_m$，转第 1 步，递归下去，直至整个句子被编码成一个节点向量表示.

其中自编码器的两个问题也是存在的，也需要用上小节的方法来解决.

即：$p = \frac{p}{||p||}$

$$E_{rae} = \frac{n_1}{n_1 + n_2} ||c_1 - c_1'||^2 + \frac{n_2}{n_1 + n_2} ||c_2 - c_2'||^2$$

---

情感监督的 RAE

通过上面两小节的方法，我们已经将句子编码成一串向量了，下面就需要用这个特征向量做情感分类，分类的方法就比较多了，SVM、logistic回归、神经网络、softmax、高斯判别法等等其实都可以.

自编码器能提取出节点中特定的结构，而我们要应用于情感分类，就需要自编码器能提取出特定的情感结构，于是我们可以扩展 RAE ，如下图，在其顶层加上 softmax 层去预测该句子的情感分布：

$$d(p;\theta) = softmax(W^{label} p)$$
假设有 $K$ 个情感类别，$d \in R^K$ 是一个 $K$ 维的向量，其中 $\sum_{k=1}^K d_k = 1$；$\theta = (w^{(1)},w^{(2)},b^{(1)},b^{(2)})$ .

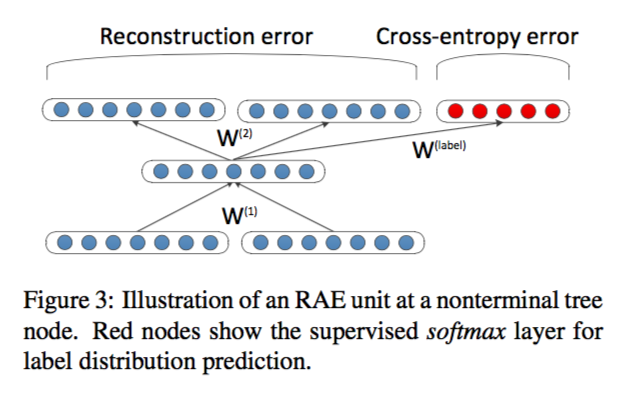
softmax层输出的是条件概率：$d_k = p(k | [c_1;c_2])$，则交叉熵误差为：

$$E_{cE}(p,t;\theta) = -\sum_{k=1}^K t_k \log{d_k (p;\theta)}$$

---

如果使用交叉熵误差来描述情感分类误差和重建误差，则最后基于情感监督的递归自编码模型通过预料库中（句子，情感标签）对 $(x,t)$ 来描述：

$$J = \frac{1}{N} \sum_{(x,t)} E(x,t;\theta) + \frac{\lambda}{2} ||\theta||^2$$

而句子的误差是递归树中所有节点的误差之和组成的：

$$E(x,t;\theta) = \sum_{s \in T(RAE_{\theta}(x))} E([c_1;c_2]_s,p_s,t,\theta)$$

而每一个非叶子节点的误差是由重建误差和情感分类的交叉熵误差加权和构成：

$$E([c_1;c_2]_s,p_s,t,\theta) = \alpha E_{rae}([c_1;c_2]_s;\theta) + (1 - \alpha) E_{cE}(p_s,t;\theta)$$

其中，超参数 $\alpha$ 是为了权衡重建误差和情感分类的交叉熵误差的.

当最小化 softmax 层的交叉熵误差时，误差会反向传播，影响 RAE 的参数和词向量表示.

初始化的时候，单词 good 或者 bad 有相似的表征. 当训练积极或者消极的情感句子时，词向量会被更新，并且捕获少量语法和更多的情感信息.

参数的学习部分，我们发现使用 L-BFGS 能获得很好的效果.

---

java 源码分析

使用的源码 github 地址为：https://github.com/hehuihui1994/RAEs

---

参考

• http://blog.csdn.net/pi9nc/article/details/27711441
• http://www.doc88.com/p-2922802917854.html
• http://www.docin.com/p-1521106821.html
• http://blog.csdn.net/neighborhoodguo/article/details/47193885
• http://blog.csdn.net/qq_26609915/article/details/52119512
• http://www.socher.org/uploads/Main/SocherPenningtonHuangNgManning_EMNLP2011.pdf
• http://datartisan.com/article/detail/48.html
• 《情感分类研究进展》
• https://hehuihui1994.github.io/hehuihui1994.github.io/2016/08/26/RAEs/#5-%E6%97%A0%E7%9B%91%E7%9D%A3RAE%E6%96%B9%E6%B3%95%EF%BC%88%E9%87%8D%E7%82%B9%EF%BC%89