[关闭]
@evilking 2018-05-01T09:49:12.000000Z 字数 12776 阅读 3122

NLP

双数组字典树

本文介绍双数组字典树的原理及实现，并讲解下在大数据集中应用时所遇到的问题及解决方法

算法优化代码已上传至 github : ImprovedDoubleArrayTrie

基础数据结构

由于双数组字典树以及优化的过程中，涉及到链表、数组、多叉树等数据结构，所以笔者会先简要回顾一下这些数据结构

数组

数组 （英语：Array），是由相同类型的元素（element）的集合所组成的数据结构，分配一块连续的内存来存储。利用元素的索引（index）可以计算出该元素对应的存储地址。

而最简单的数组就是一维数组，一维（或单维）数组是一种线性数组，其中元素的访问是以行或列索引的单一下标表示。

一维数组

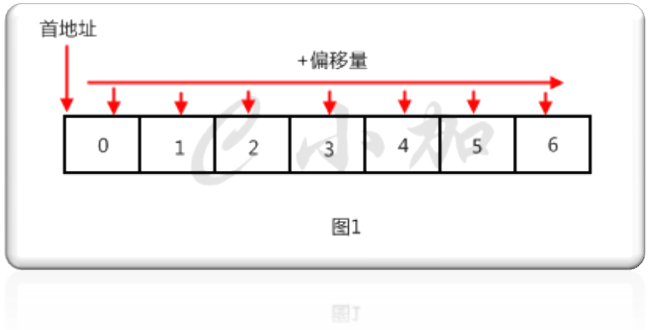
一维数组的定义C语言代码实现如下:

  1. //定义一个长度为 7 的整型数组
  2. int arr[7];

单向链表

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。

使用链表结构可以克服数组链表需要预先知道数据大小的缺点，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。

单向链表

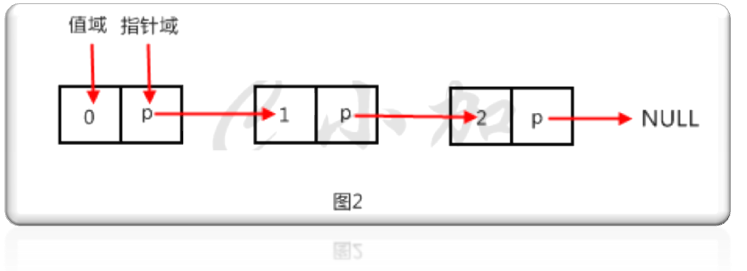
单向链表是链表中最简单的一种链表，它包含两个域，一个信息域和一个指针域。这个链接指向列表中的下一个节点，而最后一个节点则指向一个空值。节点示意图如下:

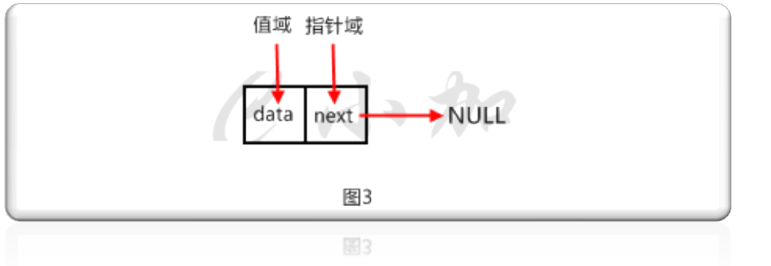
单向链表节点表示

线性表的单节点存储结构的伪码表示如下:

  1. /*线性表的单节点存储结构*/
  2. typedef struct LNode{
  3.   ElemType data;
  4.   struct LNode *next;
  5. }LNode, *q, *p;

单链表增加节点、删除节点的伪码表示如下：

  2. //q插入p之后的伪算法：
  3. r = p->next; // p->next表示的是所指向结点的指针域，指针域又是指向下一个结点的地址
  4. p->next = q; // q保存了那一块结点的地址。q是一个指针变量，存放那个结点的地址。
  5. q->next = r;
  8. //删除非循环单链表结点伪算法：
  9. //把p后面的一个结点删除掉
  10. r = p->next;
  11. p->next = p->next->next;
  12. free(r); // 释放内存

树

树 （英语：Tree）是一种无向图（undirected graph），其中任意两个顶点间存在唯一一条路径。或者说，只要没有回路的连通图就是树。森林是指互相不交并树的集合。树图广泛应用于计算机科学的数据结构中，比如二叉查找树，堆，Trie树以及数据压缩中的霍夫曼树等等。

下面是树的逻辑结构示意图:

树

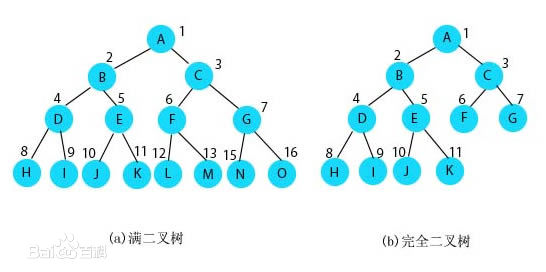
下面是树的节点 java 版本实现代码:

  1. class TreeNode{
  2.     int obj;  //当前节点的值
  4.     List<TreeNode> childList;  //子节点列表
  5. }

字典树

Trie树 也称字典树，能在常数时间O(len)内实现插入和查询操作，是一种以空间换取时间的数据结构，广泛用于词频统计和输入统计领域。

我们先以英文词典 为例，演示Trie树的结构:

  1. pool
  2. prize
  3. preview
  4. prepare
  5. produce
  6. progress

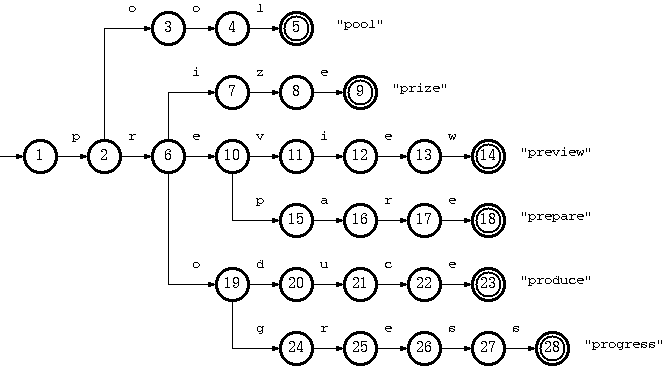
英文字典树

若换成中文，则为:

  1. 人民
  2. 人名
  3. 中国人民

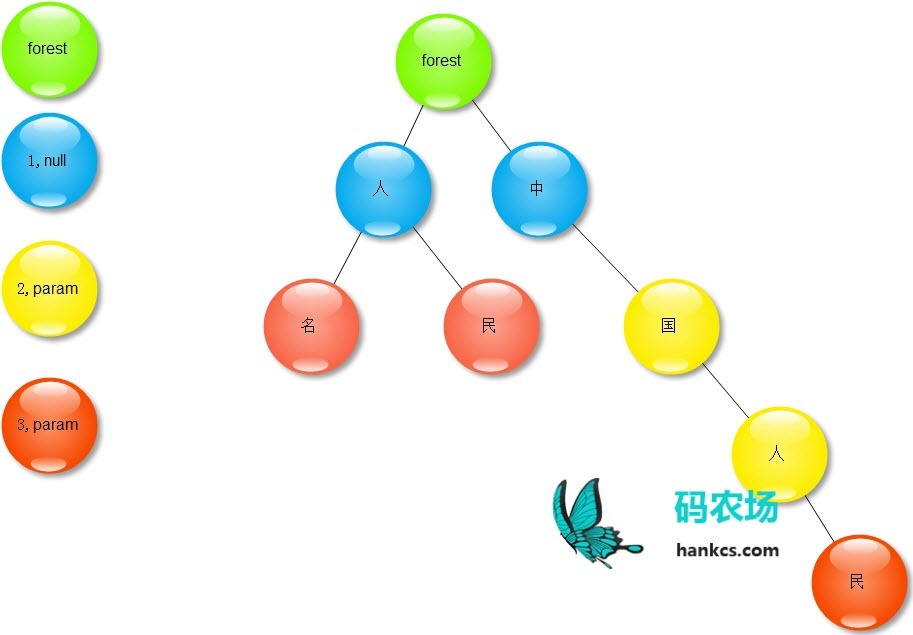
中文字典树

Trie可以理解为确定有限状态自动机，即DFA。在Trie树中，每个节点表示一个状态，每条边表示一个字符，从根节点到叶子节点经过的边即表示一个词条。查找一个词条最多耗费的时间只受词条长度影响，因此Trie的查找性能是很高的，跟哈希算法的性能相当。

双数组字典树

双数组Trie树 (DoubleArrayTrie)是一种空间复杂度低的Trie树，应用于字符区间大的语言（如中文、日文等）分词领域。

该结构由日本人JUN-ICHI AOE于1989年提出的，是Trie结构的压缩形式，同时实现了开源项目 darts-java。

Double-Array Trie 包含 base 和 check 两个数组。base数组的每个元素表示一个Trie节点，即一个状态；check数组表示某个状态的前驱状态。

base和check的关系满足下述条件：

  1. t := base[s] + c;   //状态转移，从状态s 转移到状态t
  3. if check[t] = s then
  4.     next state := t
  5. else
  6.     fail    //失败了说明有冲突，有冲突是需要重新寻找非冲突点去解决冲突
  7. endif

其中，s是当前状态的下标，t是转移状态的下标，c是输入字符的数值。如图所示：

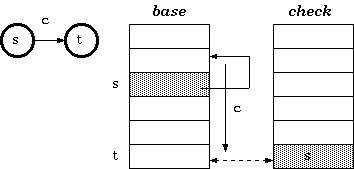
双数组字典树

双数组字典树的java实现

这里先讲解一下JUN-ICHI AOE的原始java版本实现源码

  1. private static class Node {
  2.     int code;
  3.     int depth;
  4.     int left;
  5.     int right;
  6. };
  8. private int check[];    //当前状态的父状态
  9. private int base[];     //状态数组

这里定义了 Node类，代表了字典树的节点，其中的成员变量解释如下:

这个版本的实现要求数据集按字典顺序从小到大排，否则Trie树在构建的过程中会出错，因为Node.left和Node.right不对.

以如下数据集来说明构建字典树的过程:

  1. 一举
  2. 一举一动
  3. 一举成名
  4. 一举成名天下知
  5. 万能
  6. 万能胶

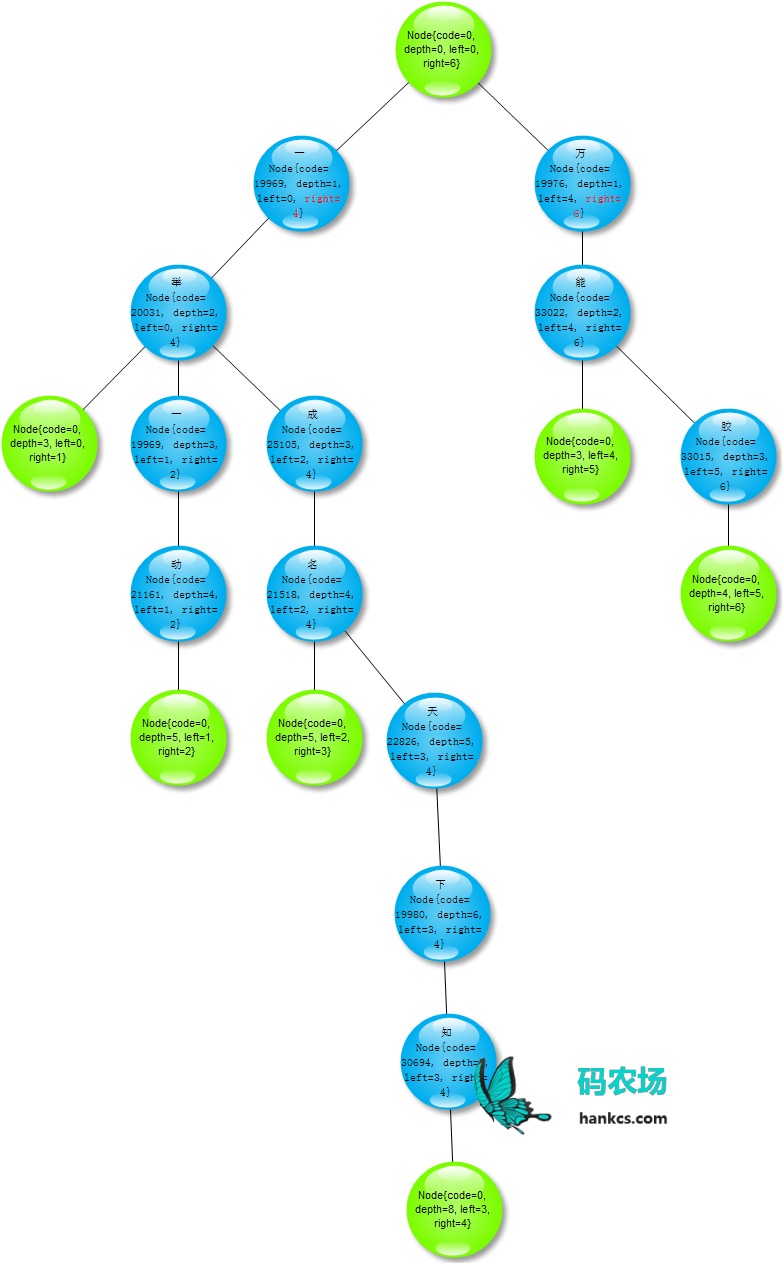
字典树构建实例

下面是具体的代码分析，首先给出构建双数组字典树的主方法:

  1. public int build(List<String> _key, int _length[], int _value[], int _keySize) {
  2.     if (_keySize > _key.size() || _key == null)
  3.         return 0;
  5.     // progress_func_ = progress_func;
  6.     key = _key;
  7.     length = _length;
  8.     keySize = _keySize;
  9.     value = _value;
  10.     progress = 0;
  12.     //由于check和base是用数组来实现的，所以当数据量增大时，需要扩大数组
  13.     resize(65536 * 32); 
  15.     //先初始化初始状态
  16.     base[0] = 1;
  18.     //当冲突率比较大时，可以跳过冲突区
  19.     nextCheckPos = 0;
  21.     //构建字典树，初始化根节点
  22.     Node root_node = new Node();
  23.     root_node.left = 0;
  24.     root_node.right = keySize;
  25.     root_node.depth = 0;
  27.     //先扫描数据集，获取根节点的所有子节点
  28.     List<Node> siblings = new ArrayList<Node>();
  29.     fetch(root_node, siblings);
  31.     //然后根据子节点集去构建双数组，其中用到了递归
  32.     insert(siblings);
  34.     //最后释放中间数据结构的占用内存
  35.     used = null;
  36.     key = null;
  38.     return error_;
  39. }

这是获取当前节点的所有子节点的代码:

  1. private int fetch(Node parent, List<Node> siblings) {
  2.     if (error_ < 0)
  3.         return 0;
  5.     int prev = 0;
  7.     //父节点的子节点集的索引边界
  8.     for (int i = parent.left; i < parent.right; i++) {
  9.         if ((length != null ? length[i] : key.get(i).length()) < parent.depth)
  10.             continue;
  11.         String tmp = key.get(i);    //数据集的第i行字符串
  12.         int cur = 0;
  13.         if ((length != null ? length[i] : tmp.length()) != parent.depth)
  14.             cur = (int) tmp.charAt(parent.depth) + 1;   //按层添加
  16.         if (prev > cur) {
  17.             error_ = -3;
  18.             return 0;
  19.         }
  21.         //遇到一个未添加的子节点
  22.         if (cur != prev || siblings.size() == 0) {
  23.             Node tmp_node = new Node();
  24.             tmp_node.depth = parent.depth + 1;  //父节点的子节点
  25.             tmp_node.code = cur;
  26.             tmp_node.left = i;
  27.             if (siblings.size() != 0) {
  28.                 //左兄弟节点的右边界更新为当前节点的左边界
  29.                 siblings.get(siblings.size() - 1).right = i;
  30.             }
  31.             siblings.add(tmp_node);
  32.         }
  33.         prev = cur;
  34.     }
  36.     if (siblings.size() != 0)
  37.         siblings.get(siblings.size() - 1).right = parent.right;
  39.     return siblings.size();
  40. }

这里可以看出，在查找当前节点的子节点集的过程中，需要反复扫描数据集.

  1. private int insert(List<Node> siblings) {
  2.     if (error_ < 0)
  3.         return 0;
  5.     //初始状态索引
  6.     int begin = 0;
  7.     //初始化合适的开始位置，防止每次都从头开始检查非冲突点
  8.     int pos = ((siblings.get(0).code + 1 > nextCheckPos) ? siblings.get(0).code + 1
  9.                 : nextCheckPos) - 1;
  10.     //为了计算冲突率
  11.     int nonzero_num = 0;
  12.     int first = 0;
  14.     outer: while (true) {
  15.         pos++;
  17.         //check数组的pos位置已经被占用，发生冲突
  18.         if (check[pos] != 0) {
  19.             nonzero_num++;
  20.             continue;
  21.         } else if (first == 0) {
  22.             nextCheckPos = pos;
  23.             first = 1;
  24.         }
  26.         //子节点的开始状态索引位
  27.         begin = pos - siblings.get(0).code;
  29.         //开始位被占用
  30.         if (used[begin])
  31.             continue;
  33.         //检查子节点是否能全部转移成功
  34.         for (int i = 1; i < siblings.size(); i++)
  35.             if (check[begin + siblings.get(i).code] != 0)
  36.                 continue outer;
  37.         break;
  38.     }
  40.     //根据冲突率，更新下一个检查点的索引位
  41.     if (1.0 * nonzero_num / (pos - nextCheckPos + 1) >= 0.95)
  42.         nextCheckPos = pos;
  44.     used[begin] = true;
  45.     size = (size > begin + siblings.get(siblings.size() - 1).code + 1) ? size
  46.                 : begin + siblings.get(siblings.size() - 1).code + 1;
  48.     //如上面双数组字典树的逻辑介绍，更新check数组和base数组的值
  49.     for (int i = 0; i < siblings.size(); i++)
  50.         check[begin + siblings.get(i).code] = begin;
  52.     for (int i = 0; i < siblings.size(); i++) {
  53.         List<Node> new_siblings = new ArrayList<Node>();
  55.         //这里表示当前节点无子节点，则说明这个字符串处理完成
  56.         //可以将base数组的字设置为负，表示字符串转移结束
  57.         if (fetch(siblings.get(i), new_siblings) == 0) {
  58.             base[begin + siblings.get(i).code] = (value != null) ? (-value[siblings
  59.                         .get(i).left] - 1) : (-siblings.get(i).left - 1);
  61.             if (value != null && (-value[siblings.get(i).left] - 1) >= 0) {
  62.                 error_ = -2;
  63.                 return 0;
  64.             }
  65.             progress++;
  66.         } else {
  67.             //这里使用了递归，去处理所有节点
  68.             int h = insert(new_siblings);
  69.             base[begin + siblings.get(i).code] = h;
  70.         }
  71.     }
  72.     return begin;
  73. }

从上面的过程大致可以看出，这个版本的实现是在构建字典树的过程中，同时去构建双数组，但是构建字典树是通过扫描数据集，获取当前节点的所有子节点去实现的.构建双数组的过程大致可以分为两部分，先去查找非冲突点，然后再做状态转移去更新base和check数组.

  1. public int exactMatchSearch(String key, int pos, int len, int nodePos) {
  2.     if (len <= 0)
  3.         len = key.length();
  4.     if (nodePos <= 0)
  5.         nodePos = 0;
  7.     int result = -1;
  9.     char[] keyChars = key.toCharArray();
  11.     //初始状态转移
  12.     int b = base[nodePos];
  13.     int p;
  15.     //按照双数组字典树的逻辑做状态转移
  16.     for (int i = pos; i < len; i++) {
  17.         p = b + (int) (keyChars[i]) + 1;
  18.         if (b == check[p])
  19.             b = base[p];
  20.         else
  21.             return result;
  22.     }
  24.     //最后的空叶子节点，去判断是否base值为负，为负就说明模式匹配成功了
  25.     p = b;
  26.     int n = base[p];
  27.     if (b == check[p] && n < 0) {
  28.         result = -n - 1;
  29.     }
  30.     return result;
  31. }

优化实现

问题 1 的现象

问题 1 的分析

问题 1 的解决

针对数据集特别大的情况，我们可以用数组链表来实现check和base双数组；数组链表是结合数组随机访问和链表不需要连续内存空间存储的优点而设计的数据结构，特别适合大数据集的添加和查找.

修改后的数据结构如下:

  1. private static final int BLOCK_SIZE = 200;  //数组块的大小
  3. private int[] value;    //保存的数组实际内容 [0,BLOCK_SIZE - 1]
  4. private int left;       //数组块的左边界   [left,right]
  5. private int right;      //数组块的右边界
  6. private NodeIntBlock next;  //数组块的下一个指针

设置值的代码如下:

  1. /**
  2.  * 设置index指向的值
  3.  * @param index
  4.  * @param val
  5.  */
  6. public void setValue(int index, int val){
  7.     //在本数组块能找到索引值
  8.     if(index >= left && index <= right){
  9.         value[index - left] = val;
  10.     }else if(next == null && index > right) { //超出数据结构边界时
  11.         next = new NodeIntBlock(right + 1); //自动创建下一个数组块
  12.         next.setValue(index, val);
  13.     }else{
  14.         next.setValue(index,val);  //到下一个数组块中查找索引并设置值
  15.     }
  16. }

查找索引的值代码如下:

  1. /**
  2.  * 返回index指向的元素
  3.  * @param index
  4.  * @return
  5.  */
  6. public int findValue(int index){
  7.     if(index >= left && index <= right){
  8.         return value[index - left];
  9.     }else if(next == null && index > right){
  10.         return 0;   //代表还未被创建的节点，对应的值当然为0了
  11.     }else{
  12.         return next.findValue(index);
  13.     }
  14. }

针对构建字典树的过程非常慢的问题，我们可以事先把字典树构建好，以节点插入的方式，而不是以扫描所有子节点的方式来构建，然后在从字典树去构建双数组，以空间换时间.

将fetch()方法换成如下代码:

  1. //先构建一颗字典树
  2. Forest forest = new Forest();   //空根节点
  3. char[] cs = null;
  4. for(String line: key){
  5.     cs = line.toCharArray();
  7.     WoodInterface tmp = forest;
  8.     for(char c: cs){
  9.         tmp = tmp.add(new Branch(c,false,null));
  10.     }
  11.     //字符串添加完后，需要添加额外的空叶子节点
  12.     tmp.add(new Branch('\000',true,null));
  13. }
  14. key = null;     //释放该列表对象，已将数据转移到了forest对象中

则空根节点与空叶子节点中间的节点串即为数据集中的字符串.

同时，在构建字典树的过程中，为当前节点插入子节点，可以对子节点进行排序，这有可以避免双数组字典树对数据集有序的要求.

优化之后，笔者用十万数据集测试，数组链表的BLOCK_SIZE设置为 200，构建完成大约需要 6.7分钟，用一千条字符串去做单模式匹配，只需要 4ms.

实际生产上，可能数据集有几千万条记录，按这个构建速度，也要好几个小时才能构建完成，依然是不能接受的

问题 2 的现象

笔者用五十万数据集去测试，构建需要好几个小时，分别去查看构建字典树的耗时和构建双数组的耗时，发现绝大部分的时间都花在了构建双数组上.

问题 2 的分析

具体来分析构建双数组的过程，上文我们讲了这一步大致分为两个过程:

那我们分别从这两处去分析:

查找非冲突点主要是通过 pos变量去循环，然后检测check数组和used数组是否发生了冲突，以及当前节点的所有子节点在转移的过程中是否会发生冲突.

由于当来了一个字符串去做转移时，都是从初始状态开始转移，但是当数据量很大时，会发现双数组前面的部分都基本被占用完了，后面需要处理的字符串会经常发生冲突，发生冲突后就需要循环遍历查找非冲突点，这就会导致效率特别低.

我们可以检测冲突的次数，定义冲突率，当冲突率达到一定阈值时，更新下一个检测点(nextCheckPos)的开始索引，这样检测下一个节点的所有子节点是否冲突时，可以跳过nextCheckPos之前的冲突区.

这里涉及到冲突率阈值的设定，如果阈值设置的小一点，则nextCheckPos更新的频繁一点，这样双数组相对来说就稀疏一些，双数组构建速度会快一些(因为冲突会少一些)，但是内存占用会多一些；如果阈值设置的大一些，那构建速度会慢一些，但是双数组密集一些，占用内存就少一些.

另外，pos增加的步长也可以修改，比如当发生几次冲突后，说明双数组当前索引附近冲突比较密集，可以适当增加pos的增长步长，这样可以快速的跳过冲突区.

状态转移时更新双数组的过程逻辑上没有哪一步可以进行优化了，但是考虑到双数组的实现是用的数组链表，则数组链表中数组块的大小可以调整.

通过测试五十万数据集，查看双数组的大小都已经到两百多万了，如果数组链表的数组块大小比较小的话，那数组的查找就需要花费大量的时间去做链表查询，这样效率会非常低，所以可以增大数据块的大小，比如设置成 十万.

问题 2 的解决

通过上面的分析，笔者优化后的代码如下:

  1. outer: while(true){
  2.     pos++;
  4.     if(check.findValue(pos) != 0){
  5.         nonzero_num++;
  6.         //第一次就冲突，说明数组比较密集了
  7.         pos = (random.nextFloat() < 0.6) ? pos + 1 : pos + 2; 
  9.         continue;
  10.     }else if(first == 0){
  11.         nextCheckPos = pos;
  12.         first = 1;
  13.     }
  15.     begin = pos - childs[0].getC();
  16.     if(used.findValue(begin)){
  17.         pos = (random.nextFloat() < 0.6) ? pos + 1 : pos + 2;
  19.         continue;
  20.     }
  22.     for(int i = 1;i < childs.length; i++){
  23.         if(check.findValue(begin + childs[i].getC()) != 0){
  24.             //其他子兄弟节点冲突，说明数组有点密集
  25.             pos = (random.nextFloat() < 0.6) ? pos : pos + 1;
  27.             continue outer;
  28.         }
  29.     }
  30.     break;
  31. }
  33. //此为冲突率，冲突率调大一点，则数组密集一点，占用内存就少一些；冲突率调小一点，则数组稀疏一些，构建快一点，但是占用内存多一些
  34. if(1.0*nonzero_num / (pos - nextCheckPos + 1) >= 0.9)
  35.     nextCheckPos = pos;    //更新下一个开始检查点，可以跳过前面一段密集区域

另外数组链表的数组块的大小修改如下:

  1. //数组块的大小，可根据数据量来调节该参数
  2. //数据量大，则参数应设置大一点，构建速度会提高很多
  3. private static final int BLOCK_SIZE = 100000;

经过上述优化修改后，笔者用一百万数据集去构建双数组，耗时约2.8分钟;用一万条记录去做模式匹配，匹配完只需要0.58秒;同时内存占用比单纯用字典树去构建减少很多很多.

多模式匹配

上文也提到过，双数组Trie的本质是一个确定有限状态自动机（DFA），每个节点代表自动机的一个状态，根据变量不同，进行状态转移，当到达结束状态或无法转移时，完成一次查询操作。

它能高速内完成单模式匹配，并且内存消耗可控，但是对多模式匹配却不理想，如果要匹配多个模式串，必须先实现前缀查询，然后频繁截取文本后缀才可多匹配，这样一份文本要回退扫描多遍，性能极低.

AC自动机能高速完成多模式匹配，然而具体实现聪明与否决定最终性能高低。大部分实现都是一个Map了事，无论是TreeMap的对数复杂度，还是HashMap的巨额空间复杂度与哈希函数的性能消耗，都会降低整体性能。

如果能用双数组Trie树表达AC自动机，就能集合两者的优点，得到一种近乎完美的数据结构。具体实现请参考《Aho Corasick自动机结合DoubleArrayTrie极速多模式匹配》。

基于模式匹配的人名识别

基于模式匹配的人名识别操作步骤:

下面给出人名词典表示例:

  1. 科主任 K 91
  2. 科员 K 16
  3. 科大 Z 7
  4. 科夫 M 3 Z 2
  5. 科学家 K 26
  6. 科学馆 L 1
  7. 科技 L 46 K 3
  8. 科技界 K 1
  9. 科教 K 5
  10. 科普 L 1

人名标签:

  1. B   //Pf    姓氏  【张】华平先生
  3. C   //Pm    双名的首字   张【华】平先生
  5. D   //Pt    双名的末字   张华【平】先生
  7. E   //Ps    单名  张【浩】说：“我是一个好人”
  9. F   //Ppf   前缀  【老】刘、【小】李
  11. G   //Plf   后缀  王【总】、刘【老】、肖【氏】、吴【妈】、叶【帅】
  13. K   //Pp    人名的上文   又【来到】于洪洋的家。
  15. L   //Pn    人名的下文   新华社记者黄文【摄】
  17. M   //Ppn   两个中国人名之间的成分 编剧邵钧林【和】稽道青说
  19. U   //Ppf   人名的上文和姓成词   这里【有关】天培的壮烈
  21. V   //Pnw   三字人名的末字和下文成词    龚学平等领导, 邓颖【超生】前
  23. X   //Pfm   姓与双名的首字成词   【王国】维、
  25. Y   //Pfs   姓与单名成词  【高峰】、【汪洋】
  27. Z   //Pmt   双名本身成词  张【朝阳】
  29. A   //Po    以上之外其他的角色
  31. S   //句子的开头

下面给出人名识别模式表:

  1. /**
  2.  * 人名识别模式串
  3.  *
  4.  * @author hankcs
  5.  */
  6. public enum NRPattern {
  7.     BBCD,
  8.     BBE,
  9.     BBZ,
  10.     BCD,
  11.     BEE,
  12.     BE,
  13.     BC,
  14.     BEC,
  15.     BG,
  16.     DG,
  17.     EG,
  18.     BXD,
  19.     BZ,
  20. //    CD,
  21.     EE,
  22.     FE,
  23.     FC,
  24.     FB,
  25.     FG,
  26.     Y,
  27.     XD,
  28. //    GD,
  29. }

开始识别，主要就是上面说的几个步骤:

  1. public static boolean Recognition(List<Vertex> pWordSegResult, WordNet wordNetOptimum, WordNet wordNetAll) {
  2.     //角色观察
  3.     List<EnumItem<NR>> roleTagList = roleObserve(pWordSegResult);
  5.     //viterbi求最可能的角色序列
  6.     List<NR> nrList = viterbiComputeSimply(roleTagList);
  8.     //模式匹配    
  9.     PersonDictionary.parsePattern(nrList, pWordSegResult, wordNetOptimum, wordNetAll);
  10.     return true;
  11. }

下面是角色观察的分析代码:

  1. /**
  2.  * 角色观察(从模型中加载所有词语对应的所有角色,允许进行一些规则补充)
  3.  * @param wordSegResult 粗分结果
  4.  * @return
  5.  */
  6. public static List<EnumItem<NR>> roleObserve(List<Vertex> wordSegResult)
  7. {
  8.     ......
  9.     tagList.add(new EnumItem<NR>(NR.A, NR.K)); //  始##始 A K
  10.     while (iterator.hasNext()){
  11.         Vertex vertex = iterator.next();
  13.         //重点就是从人名词典中获得词语的角色标注
  14.         EnumItem<NR> nrEnumItem = PersonDictionary.dictionary.get(vertex.realWord);
  15.         if (nrEnumItem == null){
  16.             switch (vertex.guessNature()){
  17.             case nr:
  18.                 // 有些双名实际上可以构成更长的三名
  19.                 if (vertex.getAttribute().totalFrequency <= 1000 && vertex.realWord.length() == 2)
  20.                 {
  21.                     nrEnumItem = new EnumItem<NR>(NR.X, NR.G);
  22.                 }
  23.                 else nrEnumItem = new EnumItem<NR>(NR.A, PersonDictionary.transformMatrixDictionary.getTotalFrequency(NR.A));
  24.                 break;
  25.             case nnt:
  26.                 // 姓+职位
  27.                 nrEnumItem = new EnumItem<NR>(NR.G, NR.K);
  28.                 break;
  29.             default:
  30.                 nrEnumItem = new EnumItem<NR>(NR.A, PersonDictionary.transformMatrixDictionary.getTotalFrequency(NR.A));
  31.                 break;
  32.             }
  33.         }
  34.         tagList.add(nrEnumItem);
  35.     }
  36.     return tagList;
  37. }

根据人名词典初步角色标注后，再使用Viterbi算法进一步求最大可能的角色标注序列；最后用角色标注序列转换成模式串:

  1. /**
  2.  * 模式匹配
  3.  *
  4.  * @param nrList         确定的标注序列
  5.  * @param vertexList     原始的未加角色标注的序列
  6.  * @param wordNetOptimum 待优化的图
  7.  * @param wordNetAll     全词图
  8.  */
  9. public static void parsePattern(List<NR> nrList, List<Vertex> vertexList, final WordNet wordNetOptimum, final WordNet wordNetAll) {
  10.     // 拆分UV
  11.     ListIterator<Vertex> listIterator = vertexList.listIterator();
  12.     StringBuilder sbPattern = new StringBuilder(nrList.size());
  14.     //设置句子的开始模式
  15.     NR preNR = NR.A;
  16.     boolean backUp = false;
  17.     int index = 0;
  18.     for (NR nr : nrList) {
  19.         ++index;
  20.         Vertex current = listIterator.next();
  22.         switch (nr) {
  23.         case U:
  24.             ......
  26.             sbPattern.append(NR.K.toString());
  27.             sbPattern.append(NR.B.toString());
  28.             preNR = B;
  30.             ......
  32.             continue;
  33.         case V:
  34.             ......
  36.             if (preNR == B) {
  37.                 sbPattern.append(NR.E.toString());  //BE
  38.             } else {
  39.                 sbPattern.append(NR.D.toString());  //CD
  40.             }
  41.             sbPattern.append(NR.L.toString());
  43.             ......
  45.             continue;
  46.         default:
  47.             sbPattern.append(nr.toString());
  48.             break;
  49.         }
  50.         preNR = nr;
  51.     }
  53.     //这里得到的是句子转换成的模式串
  54.     String pattern = sbPattern.toString();
  56.     ......
  58.     //去进行多模式匹配
  59.     trie.parseText(pattern, new AhoCorasickDoubleArrayTrie.IHit<NRPattern>() {
  60.         @Override
  61.         public void hit(int begin, int end, NRPattern value) {
  62.             //识别出的人名模式，从begin到end
  63.             StringBuilder sbName = new StringBuilder();
  64.             for (int i = begin; i < end; ++i) {
  65.                 sbName.append(wordArray[i].realWord);
  66.             }
  67.             String name = sbName.toString();
  69.             ......
  71.             int offset = offsetArray[begin];
  72.             wordNetOptimum.insert(offset, new Vertex(Predefine.TAG_PEOPLE, name, ATTRIBUTE, WORD_ID), wordNetAll);
  73.         }
  74.     });
  75. }

这样就能将人名识别出来了.

这里的人名识别的代码是摘录至 HanLP 中的命名实体识别部分，这个工具中广泛使用了双数组字典树，包括其他命名实体的识别，比如地名、组织机构名等，有兴趣的同学可以去分析分析源码.

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注