时间序列篇

序列预测

所谓预测，就是要利用序列已观察到的样本值对序列在未来某个时刻的取值进行估计.

目前对平稳序列最常用的预测方法是线性最小方差预测.线性是指预测值为观察值的线性函数，最小方差是指预测方差达到最小.

---

线性预测函数

根据 $ARMA(p,q)$ 模型的平稳性和可逆性，可以用传递性和逆转形式等级描述该序列:

$$x_t = \sum_{i=0}^{\infty}{G_i \epsilon_{t-i}} \\ \epsilon_t = \sum_{j=0}^{\infty}{I_j x_{t-j}}$$ 式中，$\{G_i\}$ 为 Green 函数值；$\{I_i\}$ 为逆转函数值.

代入可得:

$$x_t = \sum_{i=0}^{\infty} G_i \left( \sum_{j=0}^{\infty} I_j x_{t-i-j} \right) = \sum_{i=0}^{\infty} \sum_{j=0}^{\infty} G_i I_j x_{t-i-j}$$ 显然 $x_t$ 是历史数据 $x_{t-1}, x_{t-2},\cdots$ 的线性函数，不妨简记为: $$x_t = \sum_{i=0}^{\infty} G_i x_{t-1-i}$$ 对任意一个未来时刻 $t+l (\forall l \geq 1)$ 而言，该时刻的序列值 $x_{t+l}$ 也可以表示成它的历史数据 $x_{t+l-1},\cdots, x_{t+1},x_t,x_{t-1},\cdots$ 的线性函数: $$x_{t+l} = \sum_{i=0}^{\infty} G_i x_{t+l-1-i}$$ 但问题是其中只有部分历史信息 $x_t,x_{t-1},\cdots$ 是已知的，还有部分信息 $x_{t+l-1},\cdots, x_{t+1}$ 都是未知的.

一个有趣的现象是，根据线性函数的可加性，所有的未知历史信息 $x_{t+l-1},\cdots, x_{t+1}$ 都可以用已知历史信息 $x_t,x_{t-1},\cdots$ 的线性函数表示出来.以 $x_{t+2}$ 为例，已知

$$x_{t+2} = \sum_{i=0}^{\infty} C_i x_{t+1-i} = C_0 x_{t+1} + \sum_{i=0}^{\infty} C_{i+1} x_{t-i}$$ 式中，$x_{t+1}$是未知信息.

把 $x_{t+1} = \sum_{i=0}^{\infty} C_i x_{t-i}$代入上式，得:

$$x_{t+2} = C_0 \sum_{i=0}^{\infty} C_i x_{t-i} + \sum_{i=0}^{\infty} C_{i+1} x_{t-i} \\= \sum_{i=0}^{\infty}(C_0 C_i + C_{i+1}) x_{t-i}$$ 由此，$x_{t+2}$ 最终表示为已知历史信息 $x_t,x_{t-1},\cdots$的线性函数.

同理，对于未来任意 $l$ 时刻的序列值 $x_{t+l},(\forall l \geq 1)$，最终都可以表示成已知历史信息的线性函数，并用该函数形式估计 $x_{t+l}$ 的值:

$$\hat{x}_t(l) = \sum_{i=0}^{\infty} \hat{D}_i x_{t-i}$$ $\hat{x}_t(l)$也称为序列 $\{x_t\}$的第 $l$步预测值.

---

预测方差最小原则

用 $e_t(l)$ 衡量预测误差:

$$e_t(t) = x_{t+l} - \hat{x}_t(l)$$ 显然，预测误差越小，预测精度就越高.因此，目前最常用的预测原则是预测方差最小原则，即 $$Var_{\hat{x}_t(l)}[e_t(l)] = min{Var[e_t(l)]}$$ 因为 $\hat{x}_t(l)$ 为 $x_t,x_{t-1},\cdots$的线性函数，所以该原则也称为线性预测方差最小原则.

---

根据 $ARMA(p,q)$ 平稳模型的性质和线性函数的可加性，显然有

$$\begin{cases} x_{t+l} = \sum_{i=0}^{\infty}{G_i \epsilon_{t+l-i}} \\ \hat{x}_t(l) = \sum_{i=0}^{\infty}{\hat{D}_i x_{t-i}} = \sum_{i=0}^{\infty}{\hat{D}_i \left( \sum_{j=0}^{\infty}{G_j \epsilon_{t-i-j}} \right)} = \sum_{i=0}^{\infty}{W_i \epsilon_{t-i}} \end{cases}$$ 则 $$e_t(l) = x_{t+l} - \hat{x}_t(l) \\= \sum_{i=0}^{\infty}{G_i \epsilon_{t+l-i}} - \sum_{i=0}^{\infty}{w_i \epsilon_{t-i}} \\= \sum_{i=0}^{l-1}{G_i \epsilon_{t+l-i}} + \sum_{i=0}^{\infty}{(G_{l+i} - W_i)\epsilon_{t-i}}$$ 预测方差为: $$Var[e_t(l)] = \left[ \sum_{i=0}^{l-1} G_i^2 + \sum_{i=0}^{\infty}(G_{l+i} - W_i)^2 \right] \sigma_{\epsilon}^2 \geq \sum_{i=0}^{l-1} G_i^2 \sigma_{\epsilon}^2$$
显然，要使得预测方差达到最小，必须有 $$W_i = G_{l+i}, i = 0,1,2,\cdots$$
这时，$x_{t+l}$ 的预测值为: $$\hat{x}_t(l) = \sum_{i=0}^{\infty} G_{l+i} \epsilon_{t-i}, \forall l \geq 1$$
预测误差为: $$e_t(l) = \sum_{i=0}^{l-1} G_i \epsilon_{t+l-i}$$
由于 $\{\epsilon_t\}$ 为白噪声序列，所以: $$E[e_t(l)] = 0 \\ Var[e_t(l)] = \sum_{i=0}^{l-1} G_i^2 \sigma_{\epsilon}^2 , \forall l \geq 1$$

---

线性最小方差预测的性质

条件无偏最小方差估计值

序列值 $x_{t+l}$ 可以如下分解:

$$x_{t+l} = \left( \epsilon_{t+l} + G_1 \epsilon_{t+l-1} + \cdots + G_{l-1} \epsilon_{t+1} \right) + \left( G_l \epsilon_t + G_{l+1} \epsilon_{t-1} + \cdots \right) \\= e_t(l) + \hat{x}_t(l)$$
因为 $$\hat{x}_t(l) = \sum_{i=0}^{\infty} \hat{D}_i x_{t-i}$$
即在 $x_t,x_{t-1},\cdots$ 已知的条件下，$\hat{x}_t(l)$ 为常数，有 $$E(\hat{x}_t(l)|x_t,x_{t-1},\cdots) = \hat{x}_t(l), \\ Var(\hat{x}_t(l)|x_t,x_{t-1},\cdots) = 0$$
推导出 $$E(x_{t+l}|x_t,x_{t-1},\cdots) = \hat{E}[e_t(l) | x_t,x_{t-1},\cdots] + E[\hat{x}_t(l) | x_t,x_{t-1},\cdots ] = \hat{x}_t(l) \\ Var(x_{t+l} | x_t, x_{t-1},\cdots) = Var[e_t(l) | x_t, x_{t-1},\cdots] + Var[\hat{x}_t(l) | x_t, x_{t-1}, \cdots] \\= Var[e_t(l)]$$
这说明在预测方差最小原则下得到的估计值 $\hat{x}_t(l)$ 是序列值 $x_{t+l}$ 在 $x_t,x_{t-1},\cdots$ 已知的情况下得到的条件无偏最小方差估计值，且预测方差只与预测步长 $l$ 有关，而与预测起始点 $t$ 无关.但预测步长 $l$ 越大，预测值的方差也越大，因而为了保证预测的精度，时间序列数据通常只适合做短期预测.

---

$AR(p)$ 序列预测

在 $AR(p)$序列场合:

$$\hat{x}_t(l) = E(x_{t+l} | x_t,x_{t-1},\cdots) \\= E(\phi_1 x_{t+l-1} + \cdots + \phi_p x_{t+l-p} + \epsilon_{t+l} | x_t, x_{t-1}, \cdots) \\= \phi_1 \hat{x}_t(l-1) + \cdots + \phi_p \hat{x}_t(l - p)$$
式中: $$\hat{x}_t(k) = \begin{cases} \hat{x}_t(k) , \ \ k \geq 1 \\ x_{t+k} , \ \ \ \ k \leq 0 \end{cases}$$
预测方差为: $$Var[e_t(l)] = (1 + G_1^2 + \cdots + G_{l-1}^2 )\sigma_{\epsilon}^2$$

---

下面还是以我国邮路及农村投递线路每年新增里程数为例，演示$AR$模型预测:

> library(forecast)
> a <- read.table("data/file8.csv",sep = ",", header = T)
> x <- ts(a$kilometer, start = 1950)
> x.fit <- arima(x,order = c(2,0,0), method = "ML")
> x.fore <- forecast(x.fit,h = 5)
> x.fore
     Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
2009       9.465302 -15.02455 33.95516 -27.98870 46.91930
2010       6.214789 -23.94131 36.37089 -39.90499 52.33456
2011       8.392250 -21.76556 38.55006 -37.73015 54.51465
2012      11.677647 -19.95516 43.31046 -36.70056 60.05586
2013      12.885518 -19.44684 45.21788 -36.56256 62.33360
#系统默认输出预测图
> plot(x.fore)

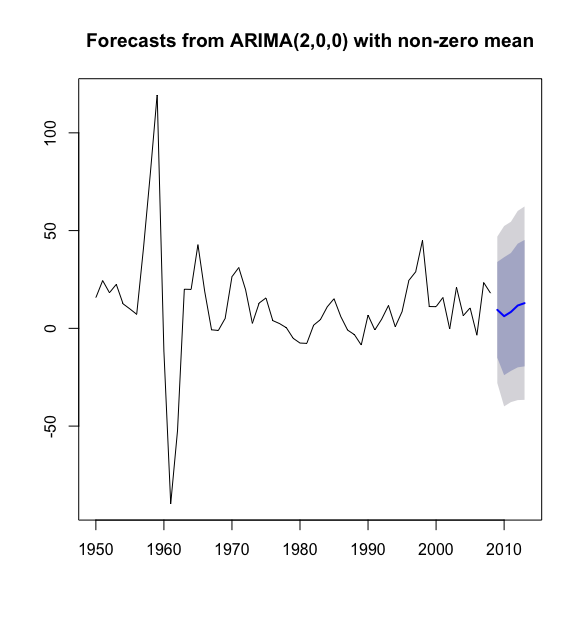
#个性化输出预测图
> L1 <- x.fore$fitted -1.96*sqrt(x.fit$sigma2)
> U1 <- x.fore$fitted + 1.96*sqrt(x.fit$sigma2)
> L2 <- ts(x.fore$lower[,2],start = 2009)
> U2 <- ts(x.fore$upper[,2],start = 2009)
> c1 <- min(x,L1,L2)
> c2 <- max(x,L2,U2)
> plot(x,type="p",pch=8,xlim=c(1950,2013),ylim=c(c1,c2))
> lines(x.fore$fitted,col=2,lwd=2)
> lines(x.fore$mean,col=2,lwd=2)
> lines(L1,col=4,lty=2)
> lines(U1,col=4,lty=2)
> lines(L1,col=4,lty=2)
> lines(L2,col=4,lty=2)
> lines(U2,col=4,lty=2)
>

---

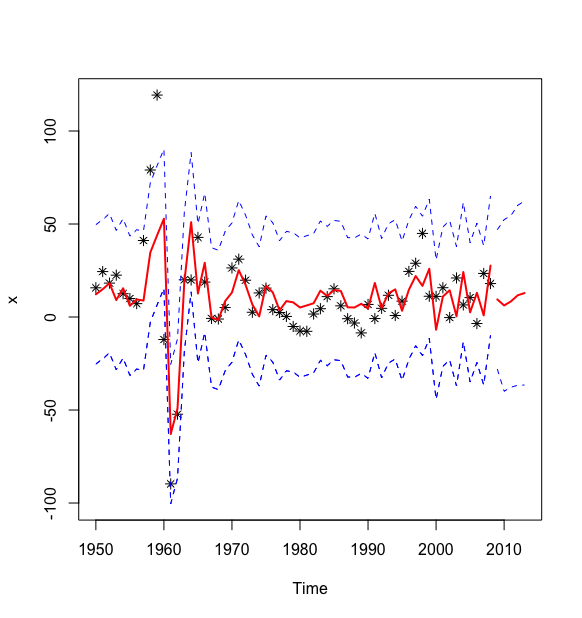
$MA(q)$ 序列预测

对一个 $MA(q)$ 序列 $x_t = \mu + \epsilon_t - \theta_1 \epsilon_{t-1} - \cdots - \theta_q \epsilon_{t-q}$ 而言，有

$$x_{t+l} = \mu + \epsilon_{t+l} - \theta_1 \epsilon_{t+l-1} - \cdots - \theta_q \epsilon_{t+l-q}$$
在 $x_t,x_{t-1},\cdots$ 已知的条件下求 $x_{t+l}$ 的估计值，就等价于在 $\epsilon_t,\epsilon_{t-1},\cdots$已知的条件下求 $x_{t+l}$ 的估计值，而未来时刻的随机扰动 $\epsilon_{t+1},\epsilon_{t+2},\cdots$ 是不可预测的，属于预测误差.

所以: 当预测步长小于等于 $MA$ 模型的阶数 $(l \leq q)$ 时，$x_{t+l}$ 可以分解为:

$$x_{t+l} = \mu + \epsilon_{t+l} - \theta_1 \epsilon_{t+l-1} - \cdots - \theta_q \epsilon_{t+l-q} \\= (\epsilon_{t+l} - \theta_1 \epsilon_{t+l-1} - \cdots - \theta_q \epsilon_{t+l-q}) + \mu \\= e_t(l) + \hat{x}_t(l)$$

即 $MA(q)$ 序列 $l$ 步的预测值为:

$$\hat{x}_t(l) = \begin{cases} \mu - \sum_{i+l}^q{\theta_i \epsilon_{t+l-i}}, l \leq q \\ \mu, l > q \end{cases}$$

这说明 $MA(q)$ 序列理论上只能预测 $q$ 步之内的序列走势，超过 $q$ 步预测值恒等于序列均值.这是由 $MA(q)$ 序列自相关 $q$ 步截尾的性质决定的.

$MA(q)$ 序列预测方差为:

$$Var[e_t(l)] = \begin{cases} (1+\theta_1^2 + \cdots + \theta_{l-1}^2) \sigma_{\epsilon}^2, l \leq q \\ (1+\theta_1^2+\cdots + \theta_q^2)\sigma_{\epsilon}^2, l > q \end{cases}$$

---

$ARMA(p,q)$序列预测

在 $ARMA(p,q)$模型场合:

$$x_t(l) = E(\phi_1 x_{t+l-1} + \cdots + \phi_p x_{t+l-p} + \epsilon_{t+l} - \theta_1 \epsilon_{t+l-1} - \cdots - \theta_q \epsilon_{t+l-q} | x_t, x_{t-1},\cdots) \\= \begin{cases} \phi_1 \hat{x}_t(l-1) + \cdots + \phi_p \hat{x}_t(l-p) - \sum_{i=l}^q \theta_i \epsilon_{t+l-i}, l \geq q \\ \phi_1 \hat{x}_t(l-1) + \cdots + \phi_p \hat{x}_t(l-p), l > q \end{cases}$$
式中: $$\hat{x}_t(k) = \begin{cases} \hat{x}_t(k) , k \geq 1 \\ x_{t+k}, k < 0 \end{cases}$$
预测方差为: $$Var[e_t(l)] = (G_0^2 + G_1^2 + \cdots + G_{l-1}^2) \sigma_{\epsilon}^2$$