机器学习篇

PCA 主成分分析

主成分分析（Principle Component Analysis，简称 PCA）主要是用于降维、数据压缩，做特征提取的时候用。

在实际任务中，我们事先不确定样本的哪些属性是对我们具体的任务（比如分类、聚类等）有用，所以往往在采集数据时会先尽可能多的采集样本的特征，然后通过分析，再将对任务目标影响不大的特征去掉。

如何判定某个特征是否可以被去掉，这就是降维算法要解决的问题，降维的算法有很多，本篇主要将基于 K-L 变换的主成分分析法.

---

主成分分析引入

假定你是一个公司的财务经理，掌握了公司的所有数据，比如 “固定资产”、“流动资金”、“每一笔借贷的数额和期限”、“各种税费”、“工资支出”、“原料消耗”、“产值”、“利润”、“折旧”、“职工人数”、“职工的分工和教育程度” 等等.

如果让你介绍公司状况，你能够把这些指标和数字都原封不动地摆出去么？

当然不能！！！

你必须要把各个方面作出 高度概括，用 一两个指标简单明了地把情况汇报清楚。

俗称：捡重点的说。

那这里就涉及到两个问题了：

• 什么叫“高度概括”？

• “一两个指标”怎么选？

“高度概括”故名思意就是使用少量的话语却能表达足够丰富的内容；比如上面列举了 11 个指标，虽然每个指标都与公司的运行状况有关，但是对指标总有一个重要度排序：一些指标是特别相关的，有一些是不那么相关的；我们只要提取出其中特别相关的指标、而忽略掉其中不那么相关的指标来给领导汇报，这就是“高度概括”了。

上面说了提取出的与公司运行状况特别相关的那几个指标，它们已经能充分体现出公司运行状况了，就是所谓的“一两个指标”（专业名词叫 主成分）。如何选取呢？我们说了是这些指标与公司的运行状况都有个重要程度（或者是领导最关心的的指标），然后就有个排序，我们取前面几个靠前的指标即可.

这又有几个问题了，第一：这种“重要度”如何来定义；第二：具体选几个靠前的指标才合适.

其实“重要度”可以用样本的协方差矩阵的特征值来表示，这个计算过程涉及到 K-L变换，所以我们先介绍 K-L变换，然后由 K-L变换整理出 PCA算法的算法过程.

---

K-L变换

卡洛南-洛伊（Karhunen-Loeve）变换（K-L 变换）:

• 一种常用的特征提取方法
• 最小均方误差意义下的最优正交变换
• 适用于任意的概率密度函数
• 在消除模式特征之间的相关性、突出异方差性方面有最优的效果

根据样本数据类型的不同，又可分为：连续 K-L变换，离散 K-L 变换.

不过一般我们用的都是离散 K-L变换.

---

设 $\{ \boldsymbol{X} \}$ 是 $n$ 维随机模式向量 $\boldsymbol{X}$ 的集合，对每一个 $\boldsymbol{X}$ 可以用确定的完备归一化正交向量系 $\{ \boldsymbol{u}_j \}$ 中的正交向量展开:

$$\boldsymbol{X} = \sum_{j=1}^{\infty} a_j \boldsymbol{u}_j$$ 其中，$\boldsymbol{u}_j$ 为正交的单位向量；$a_j$ 为系数，可以看成是 $\boldsymbol{u}_j$ 张成的空间中的坐标；

降维的目的是用有限项估计 $\boldsymbol{X}$：

$$\hat{\boldsymbol{X}} = \sum_{j=1}^{d} a_j \boldsymbol{u}_j$$

这里的 $d$ 就是前面引入中说的“一两个指标”的数量

由于 $\boldsymbol{u}_j$ 是正交的单位向量，于是有:

$$\boldsymbol{u}^T_j \boldsymbol{u}_j = \begin{cases} 1, & j = i \\ 0, & j \neq i \end{cases}$$

我们优化的目标是使估计 $\hat{\boldsymbol{X}}$ 与 实际的 $\boldsymbol{X}$ 的均方误差最小:

$$\begin{array} & \xi &=& E[(\boldsymbol{X} - \hat{\boldsymbol{X}})(\boldsymbol{X} - \hat{\boldsymbol{X}})^T] \\&=& E\left[ \left( \sum_{j = d+1}^{\infty} a_j \boldsymbol{u}_j \right) \left( \sum_{j = d+1}^{\infty} a_j \boldsymbol{u}_j \right)^T \right] \\&=& E\left[ \sum_{j = d+1}^{\infty} (a_j \boldsymbol{u}_j)(a_j \boldsymbol{u}_j)^T \right] \\&=& E\left[ \sum_{j = d+1}^{\infty} a_j (\boldsymbol{u}_j \boldsymbol{u}_j^T ) a_j \right] \\&=& E\left[ \sum_{j = d+1}^{\infty} a_j^2 \right] \end{array}$$

对 $\boldsymbol{X} = \sum_{j=1}^{\infty} a_j \boldsymbol{u}_j$ 两边左乘 $\boldsymbol{u}_j^T$ :

$$\boldsymbol{u}_j^T \boldsymbol{X} = \boldsymbol{u}_j^T \sum_{j=1}^{\infty} a_j \boldsymbol{u}_j$$

因为 $\boldsymbol{u}_j$ 是正交的单位向量，有 $\boldsymbol{u}_j^T \boldsymbol{u}_i = 0$ .所以上式改写成:

$$\boldsymbol{u}_j^T \boldsymbol{X} = a_j$$

于是均方误差又可得:

$$\begin{array} & \xi &=& E\left[ \sum_{j = d+1}^{\infty} (\boldsymbol{u}_j^T \boldsymbol{X})(\boldsymbol{u}_j^T \boldsymbol{X})^T \right] \\&=& E\left[ \sum_{j = d+1}^{\infty} (\boldsymbol{u}_j^T \boldsymbol{X})(\boldsymbol{X}^T \boldsymbol{u}_j) \right] \\&=& E\left[ \sum_{j = d+1}^{\infty} \boldsymbol{u}_j^T (\boldsymbol{X} \boldsymbol{X}^T) \boldsymbol{u}_j \right] \end{array}$$

由矩阵代数的知识可知:

$$E\left[ \sum_{j = 1}^{\infty} \boldsymbol{u}_j^T \boldsymbol{X} \boldsymbol{u}_j \right] = \sum_{j=1}^{\infty} \boldsymbol{u}_j^T E[\boldsymbol{X}] \boldsymbol{u}_j$$

所以

$$\begin{array} & \xi &=& E\left[ \sum_{j = d+1}^{\infty} \boldsymbol{u}_j^T (\boldsymbol{X} \boldsymbol{X}^T) \boldsymbol{u}_j \right] \\&=& \sum_{j= d + 1}^{\infty} \boldsymbol{u}_j^T E[\boldsymbol{X} \boldsymbol{X}^T] \boldsymbol{u}_j \\&=& \sum_{j= d + 1}^{\infty} \boldsymbol{u}_j^T \boldsymbol{R} \boldsymbol{u}_j \end{array}$$

其中 $\boldsymbol{R} = E[\boldsymbol{X} \boldsymbol{X}^T]$，则 $\boldsymbol{R}$ 表示的就是样本的自相关矩阵.

因为 $\boldsymbol{u}_j$ 不同表示的是高维映射到低维空间的这种映射方式不同，从上面的表达式来看，不同的 $\boldsymbol{u}_j$ 对应着不同的均方误差，$\boldsymbol{u}_j$ 的选择应使 $\xi$ 最小.

---

由于 $\boldsymbol{u}_j$ 是正交的单位向量，所以这里是带约束的最优化问题，我们用拉格朗日乘子法求解：

令目标函数为:

$$g(\boldsymbol{u}_j) = \sum_{j=d+1}^{\infty} \boldsymbol{u}_j^T \boldsymbol{R} \boldsymbol{u}_j - \sum_{j=d+1}^{\infty} \lambda_j (\boldsymbol{u}_j^T \boldsymbol{u}_j - 1)$$

其中， $\lambda_j$ 为拉格朗日乘数.

则函数 $g(\boldsymbol{u}_j)$ 对 $\boldsymbol{u}_j$ 求导，并令导数为零，得:

$$\frac{\partial g(\boldsymbol{u}_j)}{\partial \boldsymbol{u}_j} = \boldsymbol{R} \boldsymbol{u}_j - \lambda_j \boldsymbol{u}_j = 0$$

其中，$j = d+1,\cdots,\infty$，这正是矩阵 $\boldsymbol{R}$ 与其特征值和对应特征向量的关系式.

这说明 当用 $\boldsymbol{X}$ 的自相关矩阵 $\boldsymbol{R}$ 的特征值对应的特征向量展开 $\boldsymbol{X}$ 时，截断误差最小.

这里的 $\lambda_j$ 就是上面引入中所要求的“重要度”

---

选前 $d$ 项估计 $\boldsymbol{X}$ 时引起的均方误差为:

$$\xi = \sum_{j=d+1}^{\infty} \boldsymbol{u}_j^T \boldsymbol{R} \boldsymbol{u}_j = \sum_{j=d+1}^{\infty} (\boldsymbol{u}_j \boldsymbol{R} \boldsymbol{u}_j^T) = \sum_{j=d+1}^{\infty} \lambda_j$$

$\lambda_j$ 决定截断的均方误差，$\lambda_j$ 的值小，那么 $\xi$ 也小.

因为 $\boldsymbol{R} \boldsymbol{u}_j - \lambda_j \boldsymbol{u}_j = 0$，所以 $\boldsymbol{u}_j \boldsymbol{R} \boldsymbol{u}_j^T = \lambda_j$

因此，当用 $\boldsymbol{X}$ 的正交展开式中前 $d$ 项估计 $\boldsymbol{X}$ 时，展开式中的 $\boldsymbol{u}_j$ 应当是前 $d$ 个较大的特征值对应的特征向量.

所以 $\lambda_i,i = 1,2,\cdots,d$ 为第 $i$ 个主成分的方差.

---

最后一个问题，前 $d$ 个较大特征值的 $d$ 如何选取，我们引入贡献率和累积贡献率.

• 贡献率
  第 $i$ 个主成分的方差在全部方差中所占比重 $\frac{\lambda_i}{\sum_{i=1}^p \lambda_i}$ ，称为贡献率，反映了原来 $p$ 个指标多大的信息，有多大的综合能力.

• 累积贡献率
  前 $k$ 个主成分共有多大的综合能力，用这 $k$ 个主成分的方差和在全部方差中所占比重

  $$\frac{\sum_{i=1}^k \lambda_i}{\sum_{i=1}^p \lambda_i}$$ 来描述，称为累积贡献率.

我们选取的 $d$ ，要能使前 $d$ 个主成分的累积贡献率达到一定的阈值，通常取 $85 \%$；表示选 $d$ 个主成分时，能保证可以解释 $85 \%$ 的原信息.即:

$$\frac{\sum_{i=1}^d \lambda_i}{\sum_{i=1}^p \lambda_i} >= 0.85$$

---

K-L 变换的最后一点，就是利用得到的变换矩阵，对原样本进行变换，将高维数据映射到低维.

对 $\boldsymbol{R}$ 的特征值由大到小排列:

$$\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_d \geq \lambda_{d+1} \geq \cdots$$

取前 $d$ 个特征值，则均方误差最小的 $\boldsymbol{X}$ 的近似式为:

$$\boldsymbol{X} = \sum_{j = 1}^d a_j \boldsymbol{u}_j$$

这里的 $\boldsymbol{u}_j$ 就换成了特征值 $\lambda_j$ 对应的特征向量了.

上式又被称作 K-L 展开式，写成矩阵形式为:

$$\boldsymbol{X} = \boldsymbol{U} \boldsymbol{a} \\ \boldsymbol{a} = [a_1,a_2,\cdots,a_d]^T \\ \boldsymbol{U}_{n \times d} = [\boldsymbol{u}_1,\cdots,\boldsymbol{u}_j,\cdots,\boldsymbol{u}_d]$$
其中: $\boldsymbol{u}_j = [u_{j1},u_{j2},\cdots,u_{jn}]^T$

因为:

$$\boldsymbol{U}^T \boldsymbol{U} = \left[ \begin{matrix} \boldsymbol{u}_1^T \\ \boldsymbol{u}_2^T \\ \vdots \\ \boldsymbol{u}_d^T \end{matrix} \right] \left[ \begin{matrix} \boldsymbol{u}_1 ,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_d \end{matrix} \right] = \boldsymbol{I}$$

于是对 $\boldsymbol{X}$ 两边左乘 $\boldsymbol{U}^T$ 有

$$\boldsymbol{a} = \boldsymbol{U}^T \boldsymbol{X}$$

则系数向量 $\boldsymbol{a}$ 就是变换后的模式向量，我们令 $\boldsymbol{X}^* = \boldsymbol{a}$，即为我们所求: 将样本在高维特征空间映射到低维特征空间的模式（特征）向量.

---

PCA算法

数据预处理

PCA算法应用的场景往往是样本有多个维度，而实际应用中不同的维度的数据量纲很可能是不同的，如果直接套用上面的 K-L 变换，则会有问题，因为量纲不同计算出了 样本协方差矩阵就有问题；所以我们在套用 K-L 变换之前先得做一下数据归一化处理.

数据归一化方法很多，下面列举出两个比较常用的:

• min-max 标准化
  

  $$x^* = \frac{x - min}{max - min}$$ 是对原始数据的线性变换，使结果落到 $[0,1]$ 区间.
  其中，$max$ 为样本数据的最大值，$min$ 为样本数据的最小值.

• z-score 标准化
  

  $$x^* = \frac{x - \mu}{\sigma}$$ 其中，$\mu$ 为所有样本数据的均值，$\sigma$ 为所有样本数据的标准差.

  z-score标准化方法适用于属性的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况.

我们以 z-score标准化 来结合 K-L 变换 具体说:

设有 $n$ 个样本，每个样本观测 $p$ 个指标（变量）: $\boldsymbol{X}_1,\boldsymbol{X}_2,\cdots,\boldsymbol{X}_n$ 得到原始数据矩阵:

$$\boldsymbol{X} = \left[ \begin{matrix} x_{11},x_{12},\cdots,x_{pn} \\ x_{21},x_{22},\cdots,x_{pn} \\ \vdots,\vdots,,\vdots \\ x_{p1},x_{p2},\cdots,x_{pn} \end{matrix} \right]_{p \times n}$$ 其中 $$\boldsymbol{X}_1 = [x_{11},x_{21},\cdots,x_{p1}] \\ \boldsymbol{X}_2 = [x_{12},x_{22},\cdots,x_{p2}] \\ \vdots \\ \boldsymbol{X}_n = [x_{1n},x_{2n},\cdots,x_{pn}]$$

先计算样本均值:

$$\boldsymbol{\overline{X}} = \frac{1}{n} (\boldsymbol{X}_1 + \boldsymbol{X}_2 + \cdots + \boldsymbol{X}_n)$$

均值是对应维度相加

然后是样本标准差:

$$\boldsymbol{\sigma} = \sqrt{E[(X - \boldsymbol{\overline{X}})(X - \boldsymbol{\overline{X}})^T]}$$

每个维度依然是单独计算标准差

z-score 标准化:

$$\boldsymbol{X}' = \frac{\boldsymbol{X} - \boldsymbol{\overline{X}}}{\boldsymbol{\sigma}}$$

同样是每个维度单独算.

---

于是给出 PCA算法 的算法描述:

输入: $n$ 个 $p$ 维的样本集 $\boldsymbol{X}$ .
输出: 降维成 $d$ 维的模式向量集 $\boldsymbol{X}^*$

1. 使用数据归一化方法，比如 z-score标准化 将样本集归一化.
   

   $$\boldsymbol{X}' = \frac{\boldsymbol{X} - \boldsymbol{\overline{X}}}{\boldsymbol{\sigma}}$$

2. 计算样本协方差:

   $$\boldsymbol{R} = \frac{1}{n-1} \boldsymbol{X'} \boldsymbol{X'}^T$$

3. 计算样本协方差的特征值和特征向量.
   

   $$\boldsymbol{R} \boldsymbol{u} = \boldsymbol{\lambda} \boldsymbol{u}$$ 则，$\boldsymbol{\lambda}$ 称为 $\boldsymbol{R}$ 的特征值，$\boldsymbol{u}$ 称为 $\boldsymbol{R}$ 的特征向量

4. 对特征值进行排序，取前 $d$ 个；$d$ 的个数可按如下方式估算:

   $$\frac{\sum_{i=1}^d \lambda_i}{\sum_{i=1}^p \lambda_i} > \epsilon$$ 其中，一般 $\epsilon = 0.85$， 也可以适当调整.

5. 抽取这 $d$ 个特征值的特征向量构成映射矩阵 $\boldsymbol{U}$

   $$\boldsymbol{U} = [\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_d]_{p \times d}$$

6. 对样本集做降维变换

   $$\boldsymbol{X}^* = \boldsymbol{U}^T \boldsymbol{X'}$$

---

R 程序演示

使用的数据集:

year X1 X2 X3
1951  1  -2.7  -4.3
1952  -5.3  -5.9  -3.5
1953  -2  -3.4  -0.8
1954  -5.7  -4.7  -1.1
1955  -0.9  -3.8  -3.1
1956  -5.7  -5.3  -5.9
1957  -2.1  -5  -1.6
1958  0.6  -4.3  -0.2
1959  -1.7  -5.7  2
1960  -3.6  -3.6  1.3
1961  3  -3.1  -0.8
1962  0.1  -3.9  -1.1
1963  -2.6  -3  -5.2
1964  -1.4  -4.9  -1.7
1965  -3.9  -5.7  -2.5
1966  -4.7  -4.8  -3.3
1967  -6  -5.6  -4.9
1968  -1.7  -6.4  -5.1
1969  -3.4  -5.6  -2.9
1970  -3.1  -4.2  -2
1971  -3.8  -4.9  -3.9
1972  -2  -4.1  -2.4
1973  -1.7  -4.2  -2
1974  -3.6  -3.3  -2
1975  -2.7  -3.7  0.1
1976  -2.4  -7.6  -2.2

# 构造数据文件
data =  data.frame(NA)
write.csv(data,file = "psych.csv")
# 将数据覆盖到生成的 psych.csv ，然后读取
data =  read.table(file = "psych.csv",header = T)
temprature = data[,2:4]
rownames(temprature) <- data[,1]

上面先在工作空间中生成一个 "psych.csv" 文件，然后将上面的数据集复制粘贴覆盖到文件中，再用 read.table() 读取到 data 对象.

> head(temprature)
       X1   X2   X3
1951  1.0 -2.7 -4.3
1952 -5.3 -5.9 -3.5
1953 -2.0 -3.4 -0.8
1954 -5.7 -4.7 -1.1
1955 -0.9 -3.8 -3.1
1956 -5.7 -5.3 -5.9
# 计算 temp 的协方差矩阵
> (cov_temp =  cov(temprature))
         X1        X2        X3
X1 4.717062 1.0740923 1.3311231
X2 1.074092 1.3751385 0.4153846
X3 1.331123 0.4153846 3.8452462
# 提取协方差矩阵的特征值和特征向量
> (eig = eigen(cov_temp))
$values
[1] 5.954254 2.923732 1.059460
$vectors
          [,1]       [,2]        [,3]
[1,] 0.7996303 -0.5320980  0.27832205
[2,] 0.2375912 -0.1453204 -0.96043345
[3,] 0.5514906  0.8341185  0.01021915
#k = 2
# 累积贡献率所占的比例
> epsilon = 0.8
# 循环查找，选择合适的 k
> for(k in seq(length(eig$values))){
+     if(sum(eig$values[1:k])/sum(eig$values) > epsilon){
+         break
+     }
+ }
# 输出第一个能使累积贡献率大于指定阈值的 k
> print(k)
[1] 2
# 将数据框转换成矩阵，方便后面做矩阵乘法，降维映射
> temp_matrix = as.matrix(temprature)
# 将数据集映射到低维，生成模式向量
> temp_x = temp_matrix %*% t(eig$vectors[1:k,])
# 查看映射后的结果
> head(temp_x)
            [,1]      [,2]
1951  1.03951002 4.7598202
1952 -2.07278959 2.9596745
1953 -0.01278508 0.7872539
1954 -2.36318636 0.3852132
1955  0.43950671 3.3157293
1956 -3.37987339 5.0824860
>

上面的几个步骤是跟上面说的 PCA 的算法过程是一致的。

其中 eigen() 函数默认是使用 SVD 分解来提取特征值和特征向量，eig$values 的第 $i$ 个特征值对应 eig$vectors 的第 $i$ 行特征向量.

另外，上面的数据集由于量纲一样，所以不需要做数据归一化，但是如果不同的维度量纲不一致，可以先对数据集做归一化处理，如下:

# 可以根据需要对数据集进行 z-score 标准化缩放
> temprature <- scale(temprature)
> head(temprature)
             X1          X2         X3
1951  1.6168199  1.61368418 -1.0336540
1952 -1.2838932 -1.11514760 -0.6256843
1953  0.2355280  1.01675222  0.7512134
1954 -1.4680654 -0.09183568  0.5982248
1955  0.7420017  0.67564825 -0.4216995
1956 -1.4680654 -0.60349164 -1.8495934

---

R 自带的包:

# 进行 pca 计算，默认使用的是协方差矩阵
> pca <- princomp(temprature,cor = TRUE)
# 提取摘要内容
> summary(pca,loadings = T)
Importance of components:
                          Comp.1    Comp.2    Comp.3
Standard deviation     1.2729597 0.9106848 0.7417728
Proportion of Variance 0.5401421 0.2764489 0.1834090
Cumulative Proportion  0.5401421 0.8165910 1.0000000
Loadings:
   Comp.1 Comp.2 Comp.3
X1 -0.645 -0.126  0.754
X2 -0.582 -0.557 -0.592
X3 -0.495  0.821 -0.286
# 查看特征映射后的向量
> head(pca$scores)
         Comp.1      Comp.2     Comp.3
1951 -1.5008537 -1.99001328  0.5703247
1952  1.8225956  0.27507807 -0.1312651
1953 -1.1377879  0.02066993 -0.6517168
1954  0.7186056  0.74160798 -1.2474002
1955 -0.6767870 -0.83229525  0.2855476
1956  2.2571086 -1.01639554 -0.2245698
# 查看主成分的 碎石图
> screeplot(pca,type = "lines")
# 取前两个主成分
> temp_x = pca$scores[,1:2]

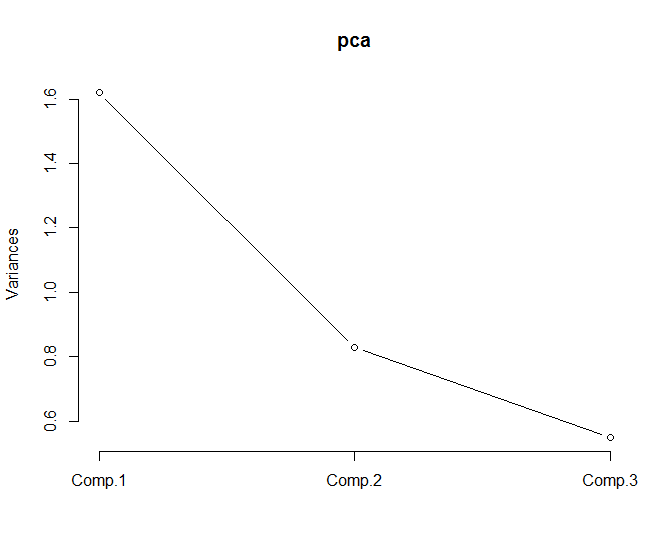
从碎石图中可以看到，一般我们选大于 1.0 的主成分，由于 Comp 2 也在 1.0 附近，所以这里我们可以选 Comp 1 和 Comp 2 作为主成分被提取出来.

---

小结

如果读者不了解协方差矩阵和 SVD分解，可以参考我们的 数学基础篇 的内容.

与 PCA 算法类似的还有 LDA(判别分析法)，我们在专门的章节中去讲.

参考

• https://wenku.baidu.com/view/0cb176f4eefdc8d377ee3250.html

• http://blog.csdn.net/lilanfeng1991/article/details/36190841

• http://blog.csdn.net/dylan_frank/article/details/74931046

• http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html

• http://blog.csdn.net/zhongkejingwang/article/details/43053513