@evilking 2018-05-02T14:56:53.000000Z 字数 6026 阅读 6174

回归分析篇

异方差性

在回归模型的基本假设中，假定随机误差项 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 具有相同的方差，独立或不相关，即对所有样本点有

$\begin{cases} E(\epsilon_i) &=& 0 \\\\ var(\epsilon_i) &=& var(\epsilon_j) \\\\ cov(\epsilon_i,\epsilon_j) &=& \begin{cases} \sigma^2 , i=j \\ 0 , i \neq j \end{cases} \end{cases}$

其中， $i,j=1,2,\cdots,n$
但在建立实际问题的回归模型时，常常存在与此假设相违背的情况:

一种是计量经济建模中常说的异方差性，即
$当时$
$var(\epsilon_i) \neq var(\epsilon_j), \ \ 当 i \neq j 时$
另一种是自相关性，即
$当时$
$cov(\epsilon_i,\epsilon_j) \neq 0, \ \ 当 i \neq j 时$

异方差产生的原因

由于实际问题的复杂性，在建立实际问题的回归分析模型时，经常会出现某一因素或一些因素随着解释变量观测值的变化而对被解释变量产生不同的影响，导致随机误差项产生不同的方差

异方差性用直观的描述不好理解，我们用一个例子来说明：

在研究城镇居民收入与购买量的关系时，我们知道居民收入与消费水平有着密切的关系。用 $x_i$ 表示第 $i$ 户的收入量， $y_i$ 表示第 $i$ 户的消费额，一个简单的消费模型为

$y_i = \beta_0 + \beta_1 x_i + \epsilon_i, \ \ i = 1,2,\cdots,n$ 在此问题中，因为各户的收入不同，消费观念和习惯的差异，通常存在明显的异方差性。一般情况下，低收入的家庭购买差异性比较小，大都购买生活必需品，但高收入的家庭购买行为差异就很大。高档消费品很多，房子、车子的规格选择余地也很大，这样购买金额的差异就很大，导致消费模型的随机项

$\epsilon_i$ 具有不同的方差.

异方差带来的问题

当一个回归问题存在异方差性时，如果任用普通最小二乘法估计未知参数，会引起严重的后果，特别是最小二乘估计量不再具有最小方差的优良性了，即最小二乘估计的有效性被破坏了

当存在异方差时，参数向量 $\boldsymbol{\beta}$ 的方差大于在同方差条件下的方差，如果用普通最小二乘法估计参数，将出现低估 $\boldsymbol{\beta}$ 的真实方差的情况。进一步将导致回归系数的 $t$ 检验值高估，可能造成本来不显著的某些回归系数变成显著。

当存在异方差时，普通最小二乘估计存在以下问题:

参数估计值虽是无偏的，但不是最小方差线性无偏估计
参数的显著性检验失效
回归方程的应用效果极不理想

异方差的检验

尽管异方差的诊断已有很多方程，但是没有一个公认的最优方法

残差图分析法

残差图分析法最直观、方便。在前面一元回归分析中的残差分析部分，我们展示了异方差性的残差图示例:

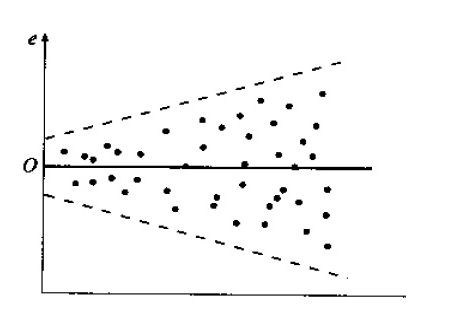
如果回归模型适合于样本数据，那么残差 $\epsilon_i$ 应反映 $\epsilon_i$ 所假定的性质，因此可以根据它来判断回归模型是否具有某些性质；

一般情况下，当回归模型满足所有假定时，残差图上的 $n$ 个点散步应是随机的，无任何规律；如果回归模型存在异方差，残差图上的点的撒布呈现出相应的趋势，如上图所示。

残差 $e$ 值也可能随 $y$ 值的增大而减小，这种情况同样属于异方差

等级相关系数法

等级相关系数法又称斯皮尔曼(Spearman)检验，这种检验方法即可用于大样本，也可用于小样本，应该较为广泛

三个步骤:

做 $y$ 关于 $x$ 的普通最小二乘回归，求出 $\epsilon_i$ 的估计值，即 $\epsilon_i$ 的值
取 $e_i$ 的绝对值，即 $|e_i|$ ，把 $x_i$ 和 $|e_i|$ 按递增或递减的次序排列后分成等级，按下式计算出等级相关系数
$r_s = 1 - \frac{6}{n(n^2 - 1)} \sum_{i=1}^n{d_i^2}$ 其中， $n$ 为样本容量， $d_i$ 为对应于 $x_i$ 和 $|e_i|$ 的等级的差数
做等级相关系数的显著性检验。在 $n > 8$ 的情况下，用下式对样本等级相关系数 $r_s$ 进行 $t$ 检验
$t = \frac{\sqrt{n - 2} r_s}{\sqrt{1 - r_s^2}}$ 如果 $t \leq t_{\alpha/2}(n-2)$ ，可以认为异方差性问题不存在，如果 $t > t_{\alpha/2}(n-2)$ ，说明 $x_i$ 与 $|e_i|$ 之间存在相关关系，异方差性问题存在

关于Spearman等级相关系数的详细计算示例，可参考维基百科中的举例: https://zh.wikipedia.org/wiki/%E6%96%AF%E7%9A%AE%E5%B0%94%E6%9B%BC%E7%AD%89%E7%BA%A7%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0

一般我们在检验异方差时，如果是人工来分析，一般用残差图法比较直观，但是不适合自动化处理

如果想自动化判断是否具有异方差性，就需要编程实现Searman等级相关系数的逻辑，实现自动化判断

一元加权最小二乘估计

当我们所研究的问题存在异方差时，线性回归模型的基本假定就被违反了，此时，就不能用普通最小二乘法进行参数估计，必须寻求适当的补救方法，对原来的模型进行变换，使变换后的模型满足同方差性假设，然后进行模型参数的估计

消除异方差性的方法通常有加权最小二乘法、Box-Cox变换法、方差稳定变换法；这里介绍加权最小二乘法

对一元线性回归方程来说，普通最小二乘法的离差平方和为

$Q(\beta_0,\beta_1) = \sum_{i=1}^n{(y_i - E(y_i))^2} = \sum_{i=1}^n{(y_i - \beta_0 - \beta_1 x_i)^2}$ 其中，每个观测值的权值相同。

在等方差的条件下，平方和中的每一项的地位是相同的。然而，在异方差的条件下，平方和中的每一项的地位是不相同的，误差项方差 $\sigma_i^2$ 大的项，在上式平方和中的作用就偏大，因而普通最小二乘估计的回归线就被拉向方差大的项，而方差小的项的拟合程度就差。加权最小二乘估计的方法是在平方和中加入一个适当的权值 $w_i$ ，以调整各项在平方和中的作用

一元线性回归的加权最小二乘的离差平方和为

$Q_w(\beta_0,\beta_1) = \sum_{i=1}^n{w_i (y_i - \hat{y_i})^2} = \sum_{i=1}^n{w_i (y_i - \beta_0 - \beta_1 x_i)^2}$ 其中，

$w_i$ 为给定的第

$i$ 个观测值的权数。

加权最小二乘法估计就是为了寻找参数 $\beta_0,\beta_1$ 的估计值 $\hat{\beta}_{0w},\hat{\beta}_{1w}$ ，使上式的离差平方和 $Q_w$ 达到极小。当然，如果所有的权值 $w_i$ 都等于一个常数，则问题就成为了普通的最小二乘法。

加权最小二乘估计为

$\begin{cases} \hat{\beta}_{0w} = \overline{y}_w - \hat{\beta}_{1w}\overline{x}_w \\\\ \hat{\beta}_{1w} = \frac{\sum_{i=1}^n{w_i(x_i - \overline{x}_w)(y_i - \overline{y}_w)}}{\sum_{i=1}^n{w_i(x_i - \overline{x}_w)^2}} \end{cases}$ 其中，

$\overline{x}_w = \frac{1}{\sum{w_i}}\sum{w_i x_i}$ 为自变量的加权平均；

$\overline{y}_w = \frac{1}{\sum{w_i}}\sum{w_i y_i}$ 为因变量的加权平均；

最后一个问题是各自变量的权值 $w_i$ 该如何选取？

为了消除异方差性的影响，为了使上式各项地位相同，观测值的权值应该是观测值误差项方差的倒数，即

$w_i = \frac{1}{\sigma_i^2}$ 其中，

$\sigma_i^2$ 为第

$i$ 个观测值误差项的方差。

所以误差项方程较大的观测值接受较小的权值，误差项方差较小的观测值接受较大的权值

但在实际问题的研究中，误差项的方差 $\sigma_i^2$ 本来就是未知的，但是当误差项方差随自变量水平以相关的形式变化时，我们可以利用这种关系

如，已知误差项方差 $\sigma_i^2$ 与 $x_i^2$ 成比例，那么 $\sigma_i^2 = k x_i^2$ ，其中 $k$ 为比例系数。权值 $w_i$ 为

$w_i = \frac{1}{k x_i^2}$ 因为比例系数

$k$ 在参数估计中可以消去，所以我们可以直接使用权值

$w_i = \frac{1}{x_i^2}$

多元加权最小二乘估计

对于一般的多元线性回归模型

$y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} + \epsilon_i, \ \ i=1,2,\cdots,n$ 当误差项

$\epsilon_i$ 存在异方差时，加权离差平方和为

$Q_w = \sum_{i=1}^n{w_i (y_i - \beta_0 - \beta_1 x_{i1} - \beta_2 x_{i2} - \cdots - \beta_p x_{ip})^2}$ 其中，

$w_i$ 为给定的第

$i$ 个观测值的权值

加权最小二乘估计就是寻找参数 $\beta_0,\beta_1,\beta_2,\cdots,\beta_p$ 的估计值 $\hat{\beta}_{0w},\hat{\beta}_{1w},\hat{\beta}_{2w},\cdots,\hat{\beta}_{pw}$ ，是上式的 $Q_w$ 达到极小，记

$\boldsymbol{W} = \left[ \begin{matrix} w_1 & & & \vdots \\ & w_2 & & \\ \vdots & & \ddots & \\ & & & w_n \end{matrix} \right]$
可以证明，加权最小二乘估计 WLS 的矩阵可表达为

$\boldsymbol{\beta}_w = (\boldsymbol{X}'\boldsymbol{W}\boldsymbol{X})^{-1}\boldsymbol{X}'\boldsymbol{W}\boldsymbol{y}$

权函数的确定方法

多元线性回归有多个自变量，通常取权函数 $W$ 为某个变量 $x_j(j=1,2,\cdots,p)$ 的幂函数，即 $W = x_j^m$

在 $x_1,x_2,\cdots,x_p$ 这p个自变量中，应该取哪一个自变量呢？

这只需要计算每个自变量 $x_j$ 与普通残差的等级相关系数，选取等级相关系数最大的自变量构造权函数即可

R程序演示异方差性检验

数据准备:

> states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> head(states)
           Murder Population Illiteracy Income Frost
Alabama      15.1       3615        2.1   3624    20
Alaska       11.3        365        1.5   6315   152
Arizona       7.8       2212        1.8   4530    15
Arkansas     10.1       2110        1.9   3378    65
California   10.3      21198        1.1   5114    20
Colorado      6.8       2541        0.7   4884   166
>

多元线性回归:

> fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)

> summary(fit)

Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost, 
    data = states)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7960 -1.6495 -0.0811  1.4815  7.6210 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.235e+00  3.866e+00   0.319   0.7510    
Population  2.237e-04  9.052e-05   2.471   0.0173 *  
Illiteracy  4.143e+00  8.744e-01   4.738 2.19e-05 ***
Income      6.442e-05  6.837e-04   0.094   0.9253    
Frost       5.813e-04  1.005e-02   0.058   0.9541    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared:  0.567, Adjusted R-squared:  0.5285 
F-statistic: 14.73 on 4 and 45 DF,  p-value: 9.133e-08

>

方法一: 残差图法

> #方法一: 残差图
> par_org =  par(mfrow = c(2,2))
> 
> plot(fit)
> 
> par(par_org)
>

残差图法

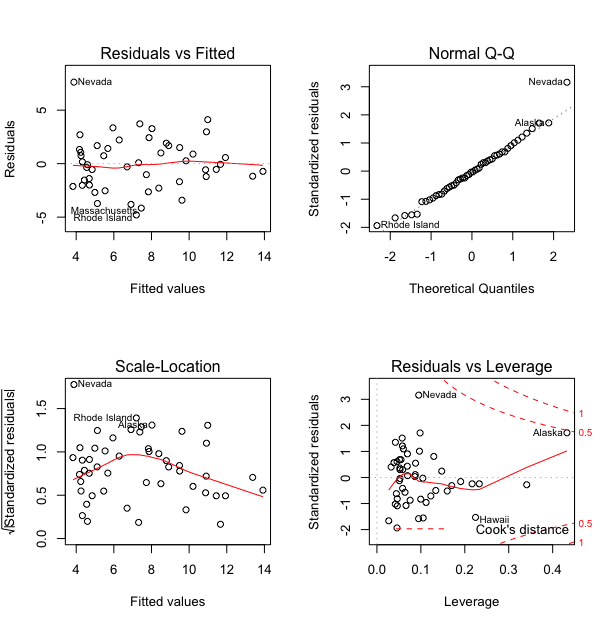
方法二: ncvTest生成计分检验

> #方法二: ncvTest生成计分检验，原假设为误差方差不变，备择假设为误差方差随拟合值水平的变化而变化

> library(car)

> #p值 < 0.05则显著，拒绝原假设
> ncvTest(fit)
Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 1.746514    Df = 1     p = 0.1863156 
> 

> #若输出结果建议幂次变换接近 1 ，则异方差不明显，即不需要进行变换；
> #若幂次变换为0.5，则用根号y代替y；
> #若幂次为0，则用对数变换
> spreadLevelPlot(fit)

Suggested power transformation:  1.209626 
>

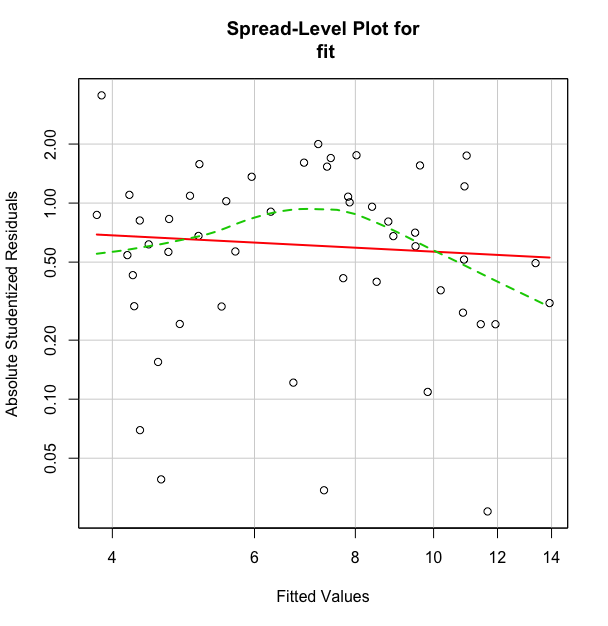
ncvTest

方法三: lmtest 的 Breusch-pagan Test

> #方法三: lmtest 的 Breusch-pagan Test
> library(lmtest)
> 
> bptest(fit, studentize = FALSE)

    Breusch-Pagan test

data:  fit
BP = 13.561, df = 4, p-value = 0.008836


> #输出学生化的残差结果，学生化具有修正异方差的作用
> bptest(fit)

    studentized Breusch-Pagan test

data:  fit
BP = 10.623, df = 4, p-value = 0.03115

>

方法四: lmtest 的 Goldfeld-Quandt Test

> #方法四: lmtest 的 Goldfeld-Quandt Test
> gqtest(fit)

    Goldfeld-Quandt test

data:  fit
GQ = 0.97047, df1 = 20, df2 = 20, p-value = 0.5264
alternative hypothesis: variance increases from segment 1 to 2

>