时间序列篇

R项目实战

数据的读取

你想要分析时间序列数据，第一件事就是将数据读入R软件，并绘制出时间序列图.

比如这个文件(https://robjhyndman.com/tsdldata/misc/kings.dat)包含着从威廉一世开始的英国国王的去世年龄数据.

#通过scan()函数将网络文件读入R
> kings <- scan("https://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
Read 42 items

> kings
 [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48 59
[27] 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56
>

scan()函数是从控制台或文件中读取数据到一个向量或列表中，完整的函数参数定义可以用help(‘scan’)语句来查看.

该文件的前三行包含了一些数据的注解内容，可以使用skip=3参数直接跳过从顶部开始的这三行注解的读取.

有关更多关于文件的操作，可参考前面R基础篇的内容进行学习

一旦你将时间序列数据读入到R中后，下一步便是将数据格式转换为时间序列格式；在R中使用ts()函数将数据存储到一个时间序列对象中去，例如:

#转换成时间序列对象
> kings_timeseries <- ts(kings)

> kings_timeseries
Time Series:
Start = 1 
End = 42 
Frequency = 1 
 [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48 59
[27] 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56
> 

这就将序列数据转换为了时间序列对象了，但是有时候时间序列数据集是少于一年的间隔相关的数据，也就是具有某种周期性，比如月度或者季度数据；这时可以使用ts()函数中的frequency参数指定收集数据在一年中的频数。比如月度数据就设定frequency = 12，季度数据就设定为frequency = 4

你还可以使用start参数来指定收集数据的第一年和这一年第一个间隔期。例如你想指定第一个时间点为1946年的第一个季度，你只需设定start = c(1946,1)

举个例子，一个样本集是从1946年1月到1959年12月的纽约每月出生人口数量（由牛顿最初收集）数据集可以从此链接下载(https://robjhyndman.com/tsdldata/data/nybirths.dat)。则读取该数据的代码为:

> births <- scan("https://robjhyndman.com/tsdldata/data/nybirths.dat")
Read 168 items

#指定时间序列的开始时间点，和频率
> births_timeseries <- ts(births,frequency = 12,start = c(1946,1))

> births_timeseries
        Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct    Nov
1946 26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901 23.175 23.227 21.672
......
1958 27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759 28.405 27.945 25.912
1959 26.076 25.286 27.660 25.951 26.398 25.565 28.865 30.000 29.261 29.012 26.992
        Dec
1946 21.870
1947 22.073
......
1958 26.619
1959 27.897
>

绘制时间序列图

当我们将时间序列的数据读入到R中后，接下来通常做的就是绘制该时间序列的序列图，可以使用plot()函数，该函数实际上会调用ts包中的plot.ts()函数.

#或者直接  plot(kings_timeseries)
> plot.ts(kings_timeseries)
>

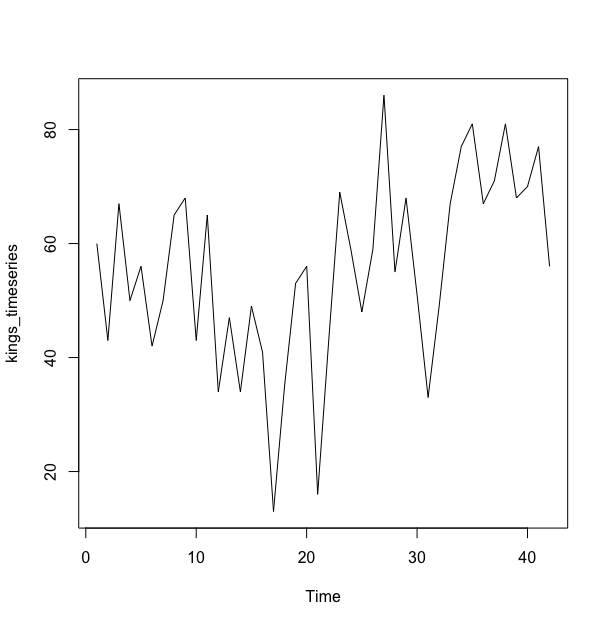
从时间曲线图可以看出，这个时间序列可以用相加模型来描述，因为在这一段时间内的随机变动大致是不变的.

类似的，我们可以画出一个纽约每月出生人口数量的时间序列图:

> plot(births_timeseries)
>

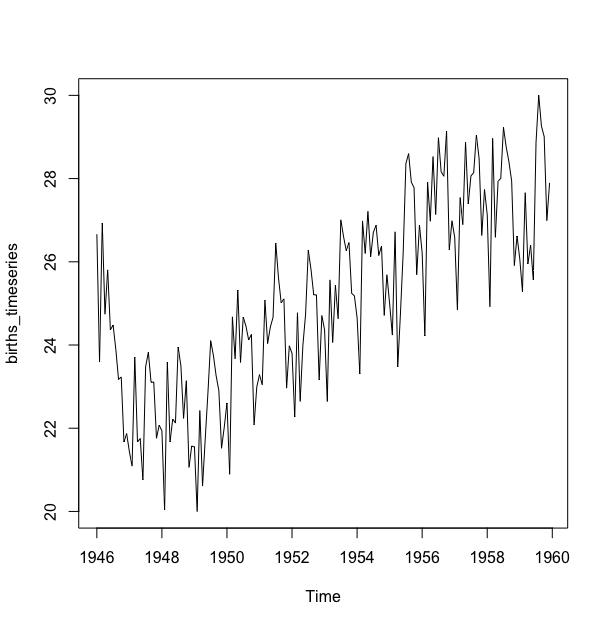
我们可以看到这个时间序列在一定月份存在的季节性变动：在每年的夏天都有一个出生峰值，在冬季的时候进入波谷（是不是说明夏天好办事，人更有激情？^_^）。同样，这样的时间序列也可能是一个相加模型，随着时间推移，季节性波动时大致稳定的而不是依赖于时间序列水平，且对着时间的变化，随机波动看起来也是大致稳定的.

对比上面两个时间序列图，如果指定了时间，序列图的横轴显示的就是时间

分解时间序列

一般序列包含一个趋势部分、一个随机部分，如果是一个季节性时间序列，则还有一个季节性部分.

分解一个时间序列意味着把它拆分成趋势部分或随机部分等等这些构成元件.

分解非季节性数据

一个非季节性时间序列包含一个趋势部分和一个不规则部分。分解时间序列即为试图把时间序列拆分成这些成分，也就是说，需要估计趋势的和不规则的这两个部分.

为了估计出一个非季节性时间序列的趋势部分，使之能够用相加模型进行描述，最常用的方法便是平滑法，比如计算时间序列的简单移动平均.

在R的"TTR"包中的SMA()函数可以用简单的移动平均来平滑时间序列数据，以kings_timeseries数据为例:

若还未安装TTR包，可以在RConsole中使用install.packages("TTR")语句安装该包

#加载 TTR 包
> library("TTR")

#跨度为3的简单移动平均
> kings_timeseries_sma3 <- SMA(kings_timeseries,n=3)

> plot(kings_timeseries_sma3)
>

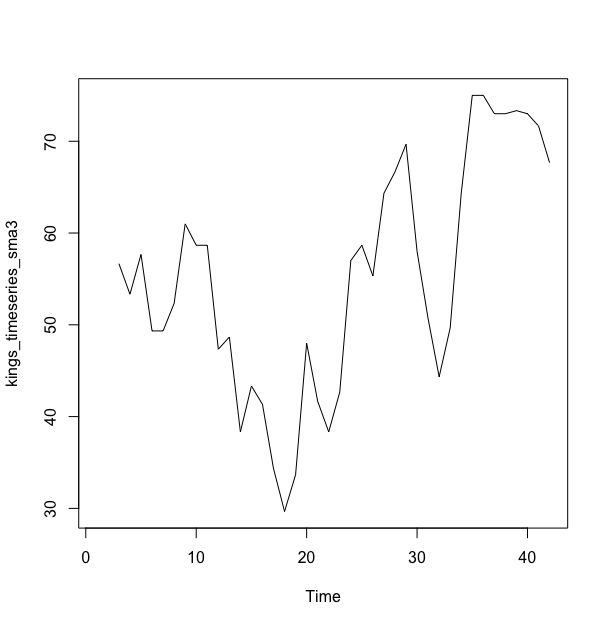
SMA()函数可以平滑时间序列数据，你需要通过参数n =来指定简单移动平均的跨度，例如上面我们采用的跨度为3

上面42位英国国王的去世年龄数据呈现出非季节性，并且由于其随机变动在整个时间段内是大致不变的，这个序列也可以被描述为一个相加模型，因此我们尝试使用了简单移动平均平滑来估计趋势部分.

当我们使用跨度为3的简单移动平均平滑后，时间序列依然呈现出大量的随机波动，因此，为了更加准确地估计这个趋势部分，我们可以尝试使用更大的跨度来平滑。

正确的跨度往往是在反复试错中获得的。例如我们使用跨度为8来实验：

#跨度为8
> kings_timeseries_sma8 <- SMA(kings_timeseries,n=8)

> plot(kings_timeseries_sma8)
>

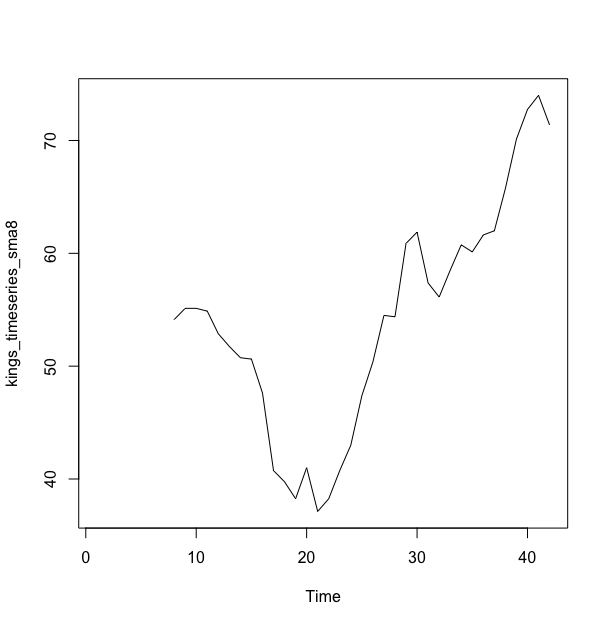
这个跨度为8的简单移动平均平滑数据的趋势部分看起来更加清晰了，我们可以发现这个时间序列前20位国王去世年龄从最初的55周岁下降到38周岁，然后一直上升到第40届国王的73周岁.

分解季节性数据

一个季节性时间序列包含一个趋势部分、一个季节性部分和一个随机部分。分解时间序列就意味着要把时间序列分解称为这三个部分：也就是估计出这三个部分.

对于可以使用相加模型进行描述的时间序列中的趋势部分和季节性部分，可以使用R中decompose()函数来估计。这个函数可以估计出时间序列中趋势的、季节性的和随机部分，而此时间序列要求是可以用相加模型来描述的.

decompose()函数返回的结果是一个列表对象，里面包含了估计出的季节性部分，趋势部分和随机部分，他们分别对应的列表对象元素为seasonal、trend和random，可以使用str()函数打印出该对象结构来查看.

我们以纽约每月出生人口数量的数据为例来演示.

人口数量是在夏季有峰值、冬季有低谷的时间序列，当季节性和随机变动在这个时间段内看起来大致不变的时候，那么此模型很有可能是可以用相加模型来描述的.

#分解时间序列
> births_timeseries_components <- decompose(births_timeseries)

#查看分解对象的数据结构
> str(births_timeseries_components)
List of 6
 $ x       : Time-Series [1:168] from 1946 to 1960: 26.7 23.6 26.9 24.7 25.8 ...
     $ seasonal: Time-Series [1:168] from 1946 to 1960: -0.677 -2.083 0.863 -0.802 0.252 ...
 $ trend   : Time-Series [1:168] from 1946 to 1960: NA NA NA NA NA ...
     $ random  : Time-Series [1:168] from 1946 to 1960: NA NA NA NA NA ...
 $ figure  : num [1:12] -0.677 -2.083 0.863 -0.802 0.252 ...
     $ type    : chr "additive"
 - attr(*, "class")= chr "decomposed.ts"
>

估计出的季节性、趋势的和随机部分被存储在变量births_timeseries_components$seasonal、births_timeseries_components$trend和births_timeseries_components$random中。我们可以将数据绘制出来，如下:

> plot(births_timeseries_components)
>

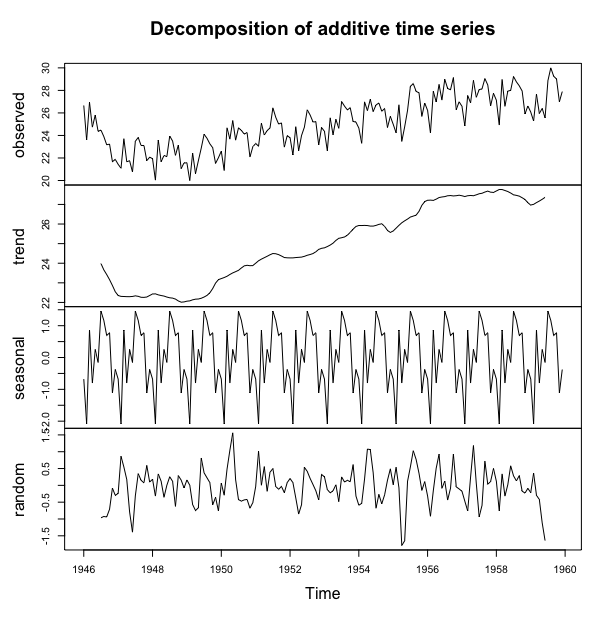
这个图展现出了原始的时间序列图（顶部），估计出的趋势部分图（第二部分），估计出的季节性部分（第三个部分），估计得不规则部分（底部）。我们可以看到估计出的趋势部分从1947年的24下降到1948年的22，紧随着是一个稳定的增加直到1949年的27.

季节性因素调整

对纽约每月出生人口数量进行季节性修正，我们可以用decompose()估计季节性部分，也可以把这个部分从原始时间序列中去除.

#从原时间序列中去除季节性部分
> births_timeseries_seasonally_adjusted <- births_timeseries - births_timeseries_components$seasonal

> plot(births_timeseries_seasonally_adjusted)
> 

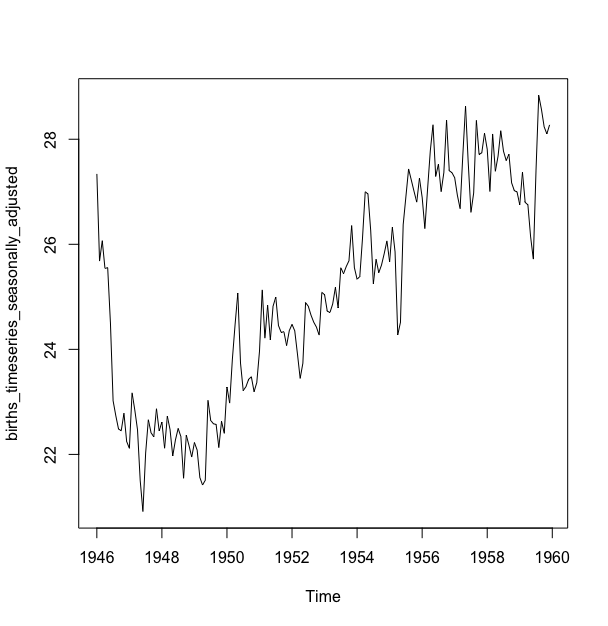
你可以看到这个去掉季节性变动的修正序列，这个季节性修正后的时间序列现在仅包含趋势部分和随机变动部分.

使用指数平滑法进行预测

指数平滑法可以用于时间序列数据的短期预测

简单指数平滑法

如果你有一个可用相加模型描述的，并且处于恒定水平和没有季节性变动的时间序列，你可以使用简单指数平滑法对其进行短期预测.

简单指数平滑法提供了一种方法估计当前时间点上的水平。为了准确的估计当前时间的水平，我们使用alpha参数来控制平滑。alpha的取值在0到1之间。当alpha越接近0的时候，临近预测的观测值在预测中的权重就越小.

例如，这个文件（https://robjhyndman.com/tsdldata/hurst/precip1.dat）包含了伦敦从1813年到1912年全部的每年每英尺降雨量（初始数据来自Hipel and McLeod，1994）。我们可以将这些数据读入R并且绘制时序图，代码如下：

> rain <- scan("https://robjhyndman.com/tsdldata/hurst/precip1.dat",skip = 1)
Read 100 items

> rain_series <- ts(rain,start = c(1813))

> plot(rain_series)
>

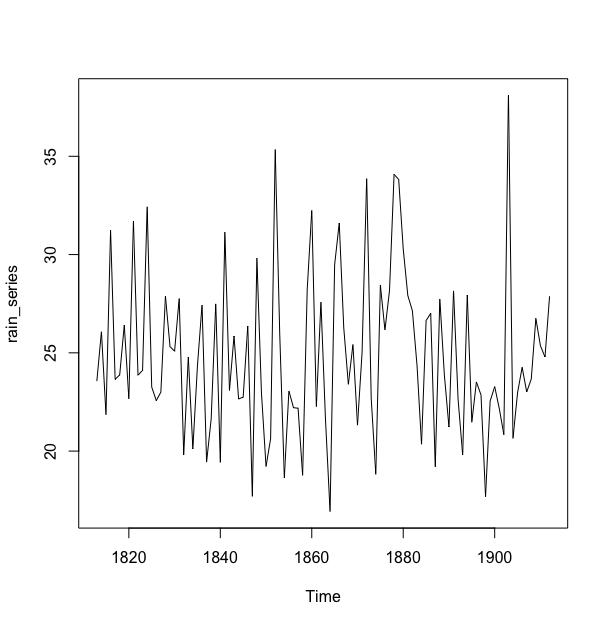
这个图可以看成整个曲线处于大致不变的水平（意思是大约保持的25英尺左右）。其随机变动在整个时间序列的范围内也可以认为是大致不变的，所以这个序列也可以大致被描述成为一个相加模型。因此，我们可以用简单指数平滑法对其进行预测.

为了能使用简单指数平滑法进行预测，我们可以使用R中的HoltWinters()函数对预测模型进行修正。该函数有参数beta=FALSE和gamma=FALSE（beta和gamma是Holt指数平滑法或者是Holt-Winters指数平滑法的参数），返回一个列表型的变量，包含了一些元素名.

例如对伦敦每年降雨量进行预测:

#简单指数平滑法
> rain_series_forecasts <- HoltWinters(rain_series,beta = FALSE,gamma = FALSE)

#查看返回结果的数据结构
> str(rain_series_forecasts)
List of 9
 $ fitted      : Time-Series [1:99, 1:2] from 1814 to 1912: 23.6 23.6 23.6 23.8 23.8 ...
      ..- attr(*, "dimnames")=List of 2
      .. ..$ : NULL
  .. ..$ : chr [1:2] "xhat" "level"
     $ x           : Time-Series [1:100] from 1813 to 1912: 23.6 26.1 21.9 31.2 23.6 ...
 $ alpha       : num 0.0241
     $ beta        : logi FALSE
 $ gamma       : logi FALSE
     $ coefficients: Named num 24.7
  ..- attr(*, "names")= chr "a"
 $ seasonal    : chr "additive"
     $ SSE         : num 1829
 $ call        : language HoltWinters(x = rain_series, beta = FALSE, gamma = FALSE)
 - attr(*, "class")= chr "HoltWinters"

#画出预测结果
> plot(rain_series_forecasts)
>

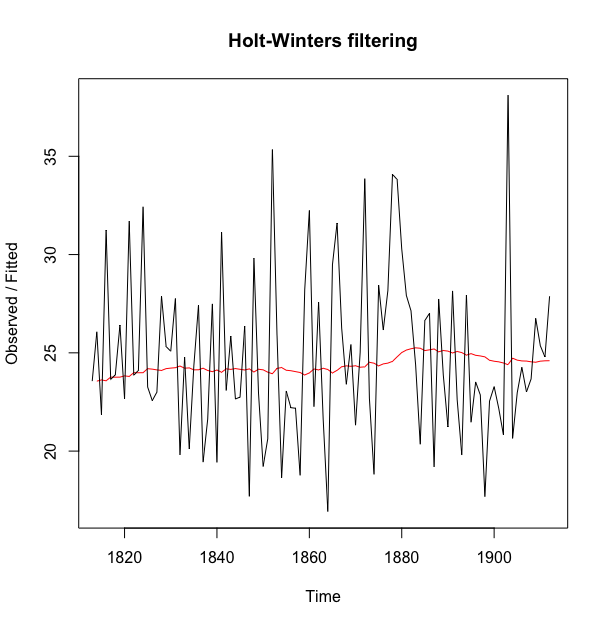
HoltWinters()的输出告诉我们alpha参数的估计值为0.024。这个数字非常接近0，告诉我们预测是基于最近的和较远的一些观测值（尽管更多的权重在现在的观测值上）.

这个图用黑色画出了原始时间序列图，用红色画出了预测的线条。在这里，预测的时间序列比原始时间序列数据平滑非常多.

默认的时候，HoltWinters()默认仅给出在原始时间序列所覆盖时期内的预测。在本案例中，原始时间序列包含伦敦1813-1912年降雨量，因此预测的时段也是1813-1912年

作为预测准确度的一个度量，我们可以计算样本内预测误差的误差平方之和，即原始时间序列覆盖的时期内的预测误差：

> rain_series_forecasts$SSE
[1] 1828.855
>

也就是说，这里的误差平方和是1828.855

如上所说，HoltWinters()函数默认仅仅是预测时期即覆盖原始数据的时期，我们可以使用R中的"forecast"包中的forecast()函数进行更远时间点上的预测.

若未安装"forecast"包，可先在RConsole中用install.packages("forecast")安装

#加载forecast包
> library("forecast")

#预测未来8年
> rain_series_forecasts2 <- forecast(rain_series_forecasts, h=8)

#查看预测结果
> rain_series_forecasts2
     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
1913       24.67819 19.17493 30.18145 16.26169 33.09470
1914       24.67819 19.17333 30.18305 16.25924 33.09715
1915       24.67819 19.17173 30.18465 16.25679 33.09960
1916       24.67819 19.17013 30.18625 16.25434 33.10204
1917       24.67819 19.16853 30.18785 16.25190 33.10449
1918       24.67819 19.16694 30.18945 16.24945 33.10694
1919       24.67819 19.16534 30.19105 16.24701 33.10938
1920       24.67819 19.16374 30.19265 16.24456 33.11182

#画出预测图形
> plot(rain_series_forecasts2)
> 

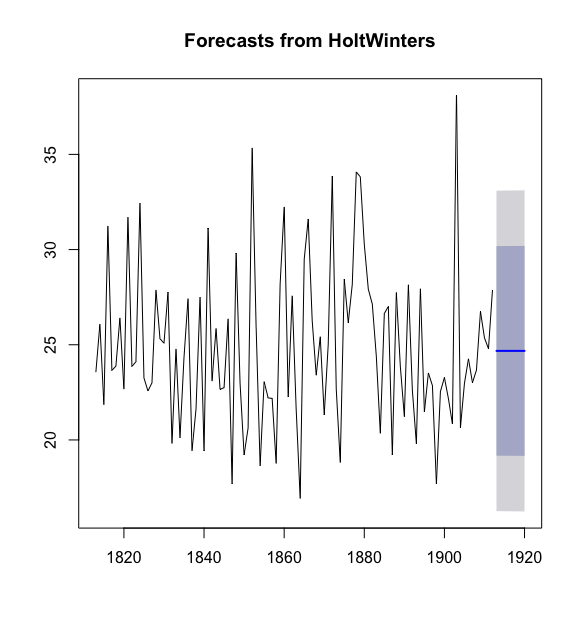
forecast()函数的参数可以通过在RConsole中用help("forecast.HoltWinters")查看；该预测是使用霍尔特-温特斯对象来预测，需要传入一个HoltWinters类的对象，例如上例中的rain_series_forecasts对象；该函数还有一个参数h，可以指定你想要做多久的预测，例如上例中我们要对未来8年的降雨量进行预测，所以h=8

forecast()函数给出了一年的预测，一个80%的预测区间和一个95%的预测区间的两个预测。例如，1920年的降雨量预测为24.67819英寸，95%的预测区间为(6.24456 33.11182)

从预测图中可以看到，蓝色线条是预测的1913-1920的降雨量，浅蓝色阴影区域为80%的预测区间，灰色阴影区域为95%的预测区间

"预测误差"是由每个时间点上的观测值减去预测值得到的。对每个时间点我们仅计算整个原始时间序列上的预测误差，即1813-1912降雨量的数据。如上所述，预测模型准确度的一个度量是样本内预测误差的误差平方和

forecast()函数返回的样本内预测误差将被存储在一个元素名为residuals的列表变量中。如果预测模型不可再被优化，连续预测中的预测误差是不相关的。换句话说，如果连续预测中的误差是相关的，很有可能需要使用另外的预测方法来进行准确预测了

为了验证是否如此，我们获取样本误差中1-20阶的相关图，可以用acf()函数计算预测误差的相关图，为了指定我们想要看到的最大阶数，可以使用acf()中的lag.max参数，若残差序列在计算指定最大阶数时出现了NA项，可以使用参数na.action=na.pass忽略NA项

例如，为了计算伦敦降雨量数据的样本内预测误差延迟1-20阶的相关图，有如下代码:

> acf(rain_series_forecasts2$residuals, lag.max = 20 ,na.action = na.pass)
> 

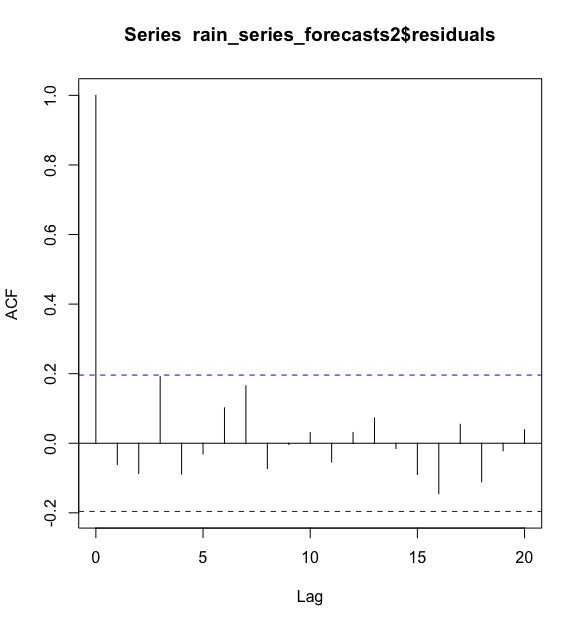
从样本相关图中看出自相关系数在3阶的时候触及了置信界限。为了验证在滞后1-20阶(lags 1-20)时的非0相关是否显著，我们使用Ljung-Box检验，通过调用Box.test()函数实现。最大阶数通过Box.test()函数中的lag参数来指定

例如，为了检验伦敦降雨量数据的样本内预测误差在滞后1-20阶(lags 1-20)是非零自相关的，输入代码:

> Box.test(rain_series_forecasts2$residuals, lag = 20, type = "Ljung-Box")

    Box-Ljung test

data:  rain_series_forecasts2$residuals
X-squared = 17.401, df = 20, p-value = 0.6268

> 

这里Ljung-Box检验统计量为17.401，并且p值为0.6268，大于0.05，并不显著，所以这并不能证明样本内预测误差在1-20阶是非0自相关的

为了确定预测模型不可继续优化，我们需要一个好的方法来检验预测误差是正态分布，并且均值为零，方差不变。为了检验预测误差是方差不变的，我们可以画一个样本内预测误差图:

> plot(rain_series_forecasts2$residuals)
> 

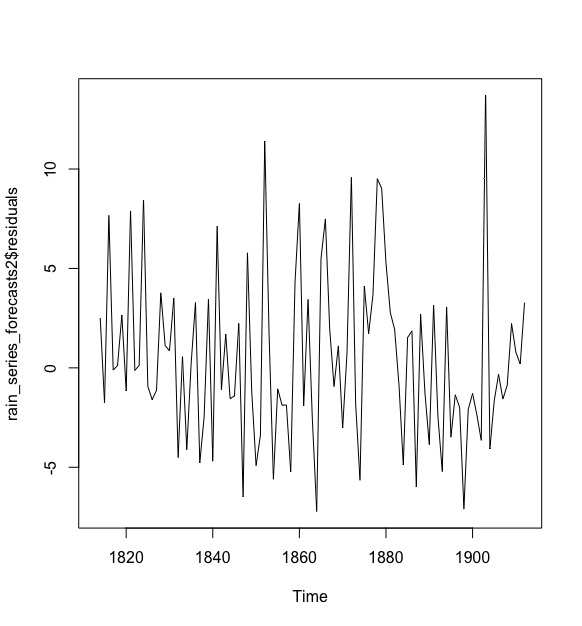
这个图展现了整个时间区域样本内预测误差似乎是方差不变的，尽管时间序列的前期(1820-1830)的波动略小于后期(如1840-1845)

为了检验预测误差是均值为零的正态分布，我们可以画出预测误差的直方图，并覆盖上均值为零、标准方差的正态分布曲线图到预测误差上。这一步需要自己编写函数，比如下面我们定义的plotForecastErrors()函数:

plotForecastErrors <- function(forecasterrors){
  #画一个红色的预测误差直方图
  mybinsize <- IQR(forecasterrors,na.rm = TRUE)/4
  mysd <- sd(forecasterrors, na.rm = TRUE)
  mymin <- min(forecasterrors, na.rm = TRUE) + mysd*5
  mymax <- max(forecasterrors, na.rm = TRUE) + mysd*3
  mybins <- seq(mymin,mymax,mybinsize)

  hist(forecasterrors, col = "red", freq = FALSE, breaks = mybins)

  #生成零均值、方差为mysd的正态分布
  mynorm <- rnorm(10000, mean = 0, sd = mysd)
  myhist <- hist(mynorm, plot = FALSE, breaks = mybins)

  #在预测误差的顶部画一条蓝色的正态曲线
  points(myhist$mids, myhist$density, type = "l", col = "blue", lwd = 2)
}

> plotForecastErrors(rain_series_forecasts2$residuals)

上图展示出预测误差大致集中分布在零附近，或多或少的接近正态分布，尽管图形看起来是一个偏向右侧的正态分布。然而，右偏是相对较小的，我们可以认为预测误差是服从均值为零的正态分布.

Ljung-Box检验的结果并不能说明样本预测误差是非零自相关的，预测误差的分布看起来也是零均值的正态分布，这暗示我们简单指数平滑法为伦敦降雨量预测提供了一个适当的模型，它是不能再被优化的.

霍尔特指数平滑法

如果你的时间序列可以被描述为一个增长或降低趋势的、没有季节性的相加模型，就可以使用霍尔特指数平滑法对其进行短期预测.

Holt指数平滑法估计当前时间点的水平和斜率。其平滑化是由两个参数控制的：alpha,用于估计当前时间点的水平；beta,用于估计当前时间点趋势部分的斜率。正如简单指数平滑法一样，alpha的beta参数都介于0到1之间，并且当参数越接近0，大多数近期的观测则将占据预测更小的权重.

一个可以用相加模型描述的有趋势的、无季节性的时间序列案例就是1866年到1911年每年女人们裙子的直径。这个数据可以从(https://robjhyndman.com/tsdldata/roberts/skirts.dat)获得.

> skirts <- scan("https://robjhyndman.com/tsdldata/roberts/skirts.dat",skip = 5)
Read 46 items

> skirts_series <- ts(skirts, start = c(1866))

> plot.ts(skirts_series)
> 

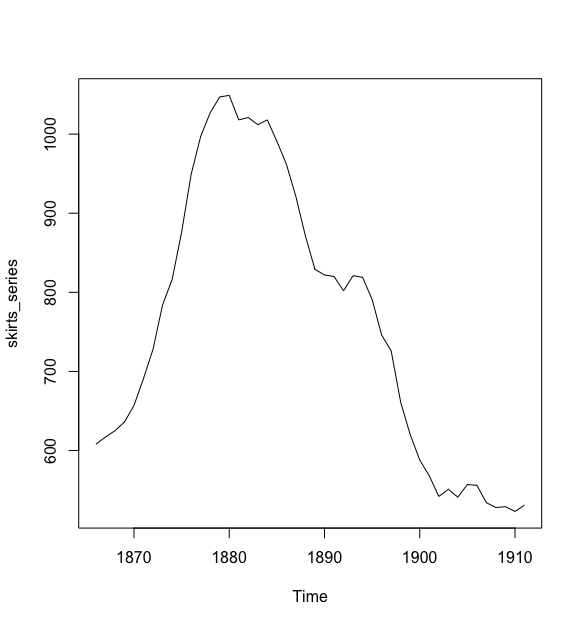
为了进行预测，我们使用HoltWinters()函数对预测模型进行调整。为了使用HoltWinters()进行Holt指数平滑法，我们需要设定其参数gamma=FALSE(gamma参数常常用于Holt-Winters指数平滑法，后文中有解释)

例如，为了使用Holt指数平滑法修正一个裙边直径的预测模型，输入代码:

> skirts_series_forecasts <- HoltWinters(skirts_series, gamma = FALSE)

> skirts_series_forecasts
Holt-Winters exponential smoothing with trend and without seasonal component.

Call:
HoltWinters(x = skirts_series, gamma = FALSE)

Smoothing parameters:
 alpha: 0.8383481
 beta : 1
 gamma: FALSE

Coefficients:
        [,1]
a 529.308585
b   5.690464

> skirts_series_forecasts$SSE
[1] 16954.18

> plot(skirts_series_forecasts)
>   

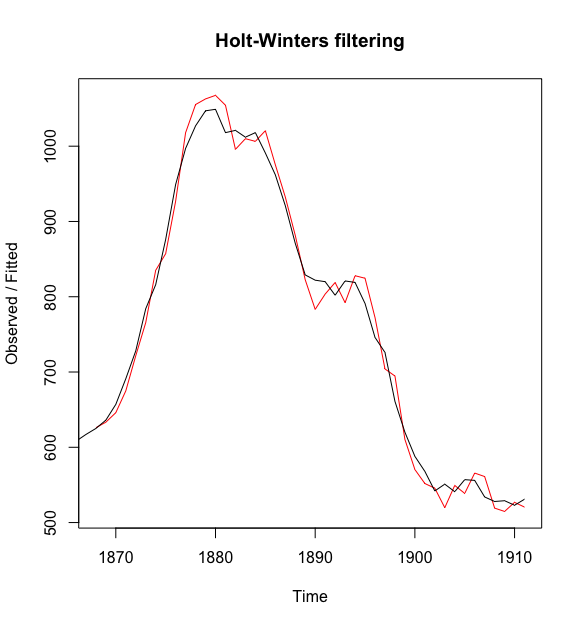
这里的alpha预测值为0.84，beta预测值为1.00。这都是非常高的值，告诉我们无论是水平上，还是趋势的斜率，当前值大部分都是基于时间序列上最近的观察值。预测样本内误差的误差平方和是16954.18

从预测结果图中可以看到，样本内预测非常接近观察值，尽管它们对于观察值来说有一点点延迟.

如果你想的话，你可以通过HoltWinters()函数中的l.start和b.start参数去指定水平和趋势的斜率的初始值。常见的设定水平初始值是让其等于时间序列的第一个值(在裙子数据中是608)，而斜率的初始值则是其第二个值减去第一个值(在裙子数据中是9)。

例如，为了使用Holt指数平滑法找到一个在裙边直径数据中合适的预测模型，我们设定其水平初始值为608，趋势部分的斜率初始值为9，代码如下:

> HoltWinters(skirts_series,gamma = FALSE, l.start = 608, b.start = 9)
Holt-Winters exponential smoothing with trend and without seasonal component.

Call:
HoltWinters(x = skirts_series, gamma = FALSE, l.start = 608,     b.start = 9)

Smoothing parameters:
 alpha: 0.8346775
 beta : 1
 gamma: FALSE

Coefficients:
        [,1]
a 529.278637
b   5.670129
> 

正如我们使用简单指数平滑法一样，可以使用"forecast"包中的forecast()函数预测未来而无需覆盖原始序列。

例如，我们有1866年到1911年的裙边直径时间序列数据，因此我们可以预测1912年到1930年(19个点或者更多)，并且画出它们，代码如下:

> skirts_series_forecasts2 <- forecast(skirts_series_forecasts, h = 12)

> plot(skirts_series_forecasts2)
> 

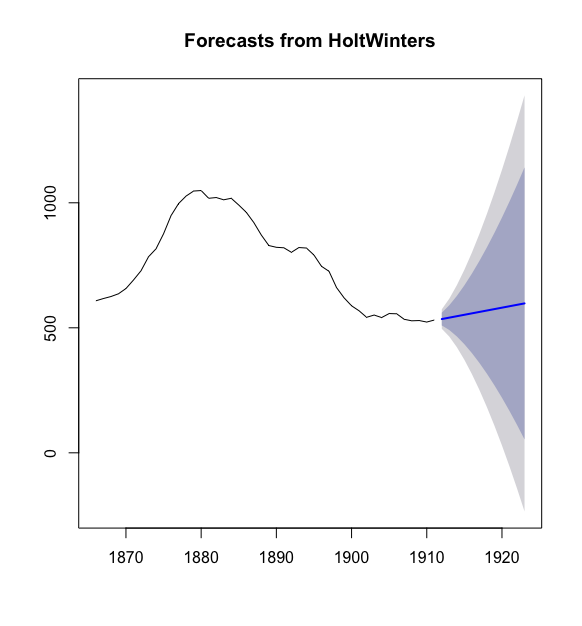
预测部分使用蓝色线条标识出来了，浅蓝色阴影区域为80%预测区域，灰色阴影区域为95%的预测区域.

和简单指数平滑法一样，我们看看样本内预测误差是否在延迟1-20阶时是非零自相关的，以此来检验模型是否还可以被优化

> acf(skirts_series_forecasts2$residuals, lag.max = 20, na.action = na.pass)

> Box.test(skirts_series_forecasts2$residuals, lag = 20, type = "Ljung-Box")

    Box-Ljung test

data:  skirts_series_forecasts2$residuals
X-squared = 19.731, df = 20, p-value = 0.4749

> 

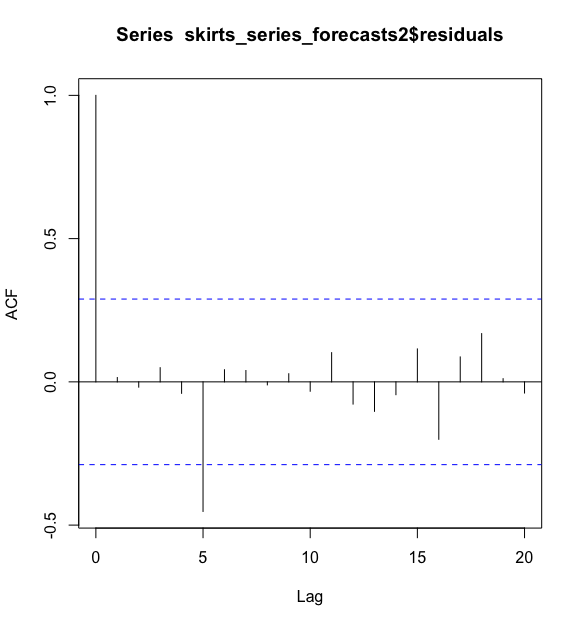
相关图呈现出样本内预测误差的样本自相关系数在滞后5阶的时候超过了置信边界。不管怎样，我们可以界定在前20滞后期中有1/20的自相关值超出95%的显著边界是偶然的，当我们进行Ljung-Box检验时，P值为0.47，意味着我们并不能证明样本内预测误差在滞后1-20阶的时候是非零自相关的.

和简单指数平滑法一样，我们应该检查整个序列中的预测误差是否是方差不变、服从零均值的正态分布

> plot(skirts_series_forecasts2$residuals)

> plotForecastErrors(skirts_series_forecasts2$residuals)

预测误差的时间曲线图告诉我们预测误差在整个时间段内是大致方差不变的。这个预测误差的直方图告诉我们预测误差似乎是零均值、方差不变的正态分布.

因此，Ljung-Box检验结果并不能说明预测误差是自相关的，而其预测误差的时间曲线图和直方图表示出似乎预测误差是服从零均值、方差不变的正态分布。因此我们可以总结出Holt指数平滑法为裙边直径提供了一个合适的预测，并且是不可再优化的.

Holt-Winters指数平滑法

如果你有一个增长或降低趋势并存在季节性的可被描述成相加模型的时间序列，你可以使用霍尔特-温特指数平滑法对其进行短期预测.

Holt-Winters指数平滑法估计当前时间点的水平，斜率和季节性部分。平滑化依靠三个参数来控制：alpha,beta和gamma，分别对应当前时间点上的水平、趋势部分的斜率和季节性部分。参数alpha、beta和gamma的取值都在0和1之间，并且当其取值越接近0时，意味着对未来的预测值而言最近的观测值占据相对较小的权重。

一个可以用相加模型描述的并附有趋势性和季节性的时间序列案例，便是澳大利亚昆士兰州的海滨纪念品商店的月度销售日志，数据可以从(https://robjhyndman.com/tsdldata/data/fancy.dat)获得

> souvenir <- scan("https://robjhyndman.com/tsdldata/data/fancy.dat")
Read 84 items

> souvenir_timeseries <- ts(souvenir, frequency = 12, start = c(1987,1))

> plot(log(souvenir_timeseries))
> 

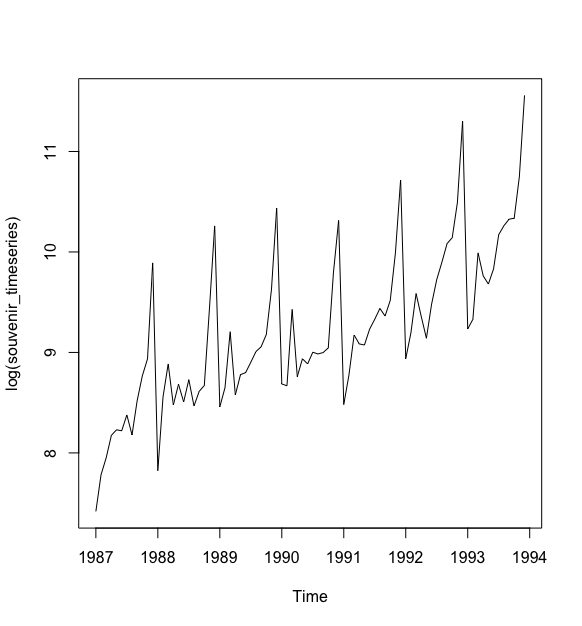
为了实现预测，我们可以使用HoltWinters()函数对预测模型进行修正。比如，我们队纪念品商店的月度销售数据预测模型进行对数变换，代码如下:

#对数变换
> log_souvenir_timeseries <- log(souvenir_timeseries)

#HoltWinters预测
> souvenir_timeseries_forecasts <- HoltWinters(log_souvenir_timeseries)

#查看预测结果
> souvenir_timeseries_forecasts
Holt-Winters exponential smoothing with trend and additive seasonal component.

Call:
HoltWinters(x = log_souvenir_timeseries)

Smoothing parameters:
 alpha: 0.413418
 beta : 0
 gamma: 0.9561275

Coefficients:
           [,1]
a   10.37661961
b    0.02996319
s1  -0.80952063
s2  -0.60576477
s3   0.01103238
s4  -0.24160551
s5  -0.35933517
s6  -0.18076683
s7   0.07788605
s8   0.10147055
s9   0.09649353
s10  0.05197826
s11  0.41793637
s12  1.18088423

#预测误差平方和
> souvenir_timeseries_forecasts$SSE
[1] 2.011491
> 

这里alpha,beta和gamma的估计值分别是0.413418,0,0.9561275。alpha是相对较低的，意味着在当前世界点估计的水平是基于最近观察和历史观测值。beta的估计是0，表明估计出来的趋势部分的斜率在整个时间序列上是不变的，并且应该等于其初始值。这是很直观的感觉，水平改变非常多，但是趋势部分的斜率b却任然大致相同。与此相反，gamma的值则很高，表明当前时间点的季节性部分的估计仅仅基于最近的观测值.

正如简单指数平滑法和Holt指数平滑法一样，我们用黑线画出原始数据的时间曲线图，用红线在上面画出预测值的时间曲线图:

> plot(souvenir_timeseries_forecasts)
> 

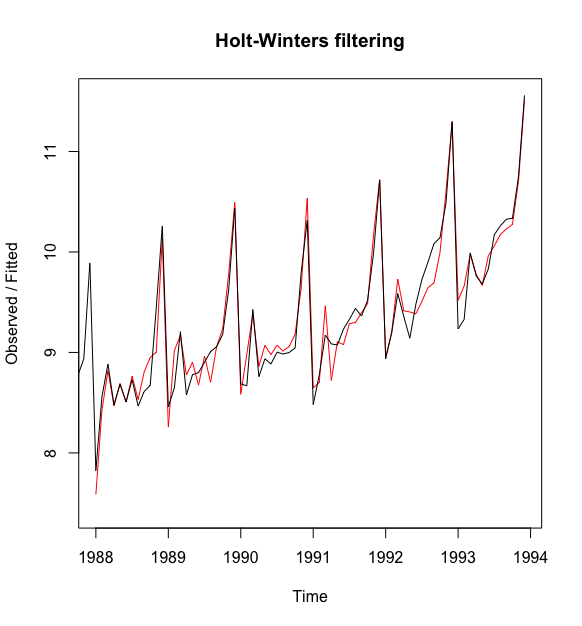
我们可以从图中看成Holt-Winters指数平滑法非常成功的预测了季节峰值，其峰值大约发生在每年的11月份.

为了预测非原始时间序列的未来一段时间，我们任然使用forecast()函数，传入HoltWinters()对象:

#预测未来48个月
> souvenir_timeseries_forecasts2 <- forecast(souvenir_timeseries_forecasts, h = 48)

> plot(souvenir_timeseries_forecasts2)
>

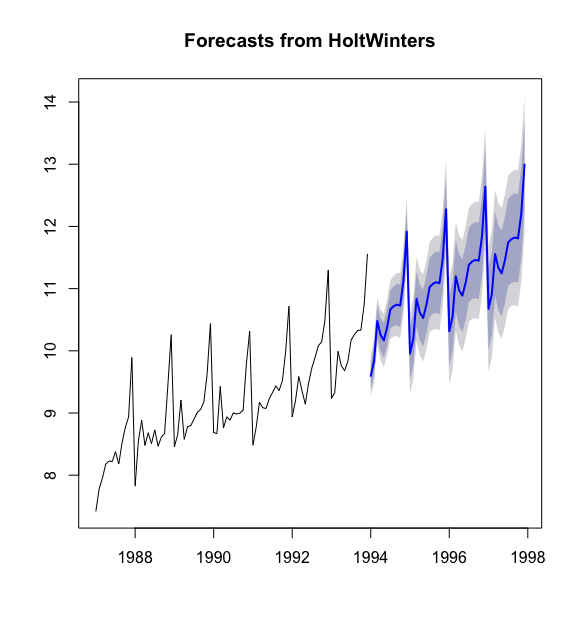
蓝色线条显示出来的是预测，浅蓝色和黑色阴影区域分别是80%和95%的预测区间.

我们可以通过画相关图和进行Ljung-box检验来检查样本内预测误差在延迟1-20阶时是否非零自相关，并以此确定预测模型是否可以再被优化

#计算自相关系数
> acf(souvenir_timeseries_forecasts2$residuals, lag.max = 20, na.action = na.pass)

#自相关性检验
> Box.test(souvenir_timeseries_forecasts2$residuals, lag = 20, type = "Ljung-Box")

    Box-Ljung test

data:  souvenir_timeseries_forecasts2$residuals
X-squared = 17.53, df = 20, p-value = 0.6183

> 

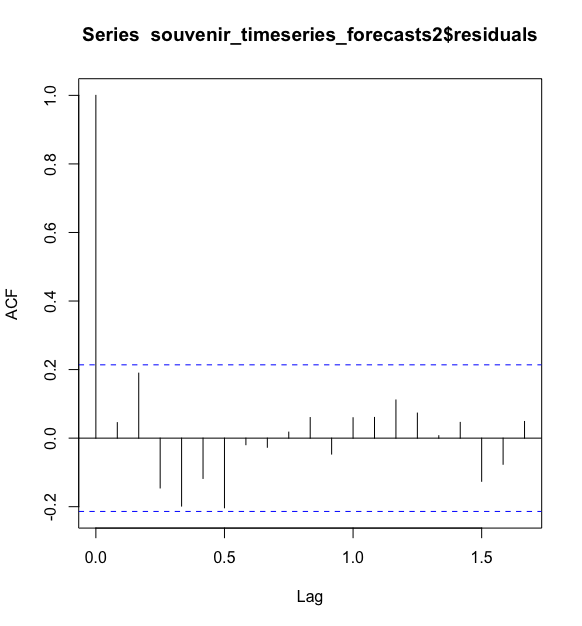
这个样本预测误差的相关图并没有在延迟1-20阶内自相关系数超过置信界限的，而且Ljung-Box检验的p值>0.05，不显著，并不能说明延迟1-20阶是非零自相关的。

我们可以在整个时间段内检验预测误差是否是方差不变，并且服从零均值的正态分布，与本文之前的方法一样:

> plot(souvenir_timeseries_forecasts2$residuals)
    > plotForecastErrors(souvenir_timeseries_forecasts2$residuals)

从这个时间曲线图看成，预测误差在整个时间段是方差不变的。从预测误差的直方图，似乎其预测误差是服从均值为零的正态分布的.这暗示着Holt-Winters指数平滑法为纪念品销售数据提供了一个合适的预测模型，并且是不可再被优化的.

ARIMA模型

指数平滑法对于预测来说非常有帮助，而且它对时间序列上面连续的值之间相关性没有要求。但是，如果你想使用指数平滑法计算出预测区间，那么预测误差必须是不相关的，而且必须是服从零均值、方差不变的正态分布。

即使指数平滑法对时间序列连续数值之间相关性没有要求，在某种情况下，我们可以通过考虑数据之间的相关性来创建更好的预测模型。

自回归移动平均模型(ARIMA)包含一个确定(explicit)的统计模型用于处理时间序列的不规则部分，它也允许不规则部分可以自相关.

时间序列的差分

ARIMA模型为平稳时间序列定义的。因此，如果你从一个非平稳的时间序列开始，首先你就需要做时间序列差分直到你得到一个平稳时间序列。如果你必须对时间序列做d阶差分才能得到一个平稳序列，那么你就使用ARIMA(p,d,q)模型，其中d是差分阶数.

在R中你可以使用diff()函数做时间序列的差分。例如，每年女人裙子边缘的直径做成的时间序列数据，从1866年到1911年在平均值上是不平稳的。随着时间增加，数值变化很大。

#一阶差分
> skirts_series_diff1 <- diff(skirts_series, differences = 1)

> plot(skirts_series_diff1)
>

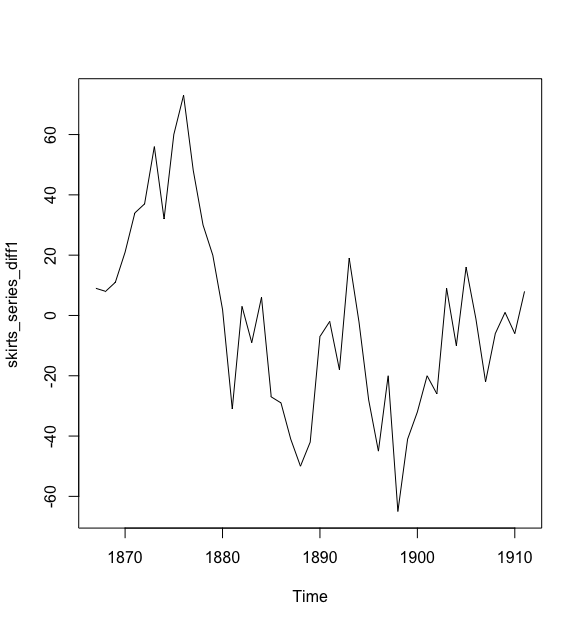
一阶差分时间序列结果的均值看起来并不平稳。因此，我们需要再次做差分，来看一下是否能得到平稳时间序列:

#二阶差分
> skirts_series_diff2 <- diff(skirts_series, differences = 2)

> plot(skirts_series_diff2)
>

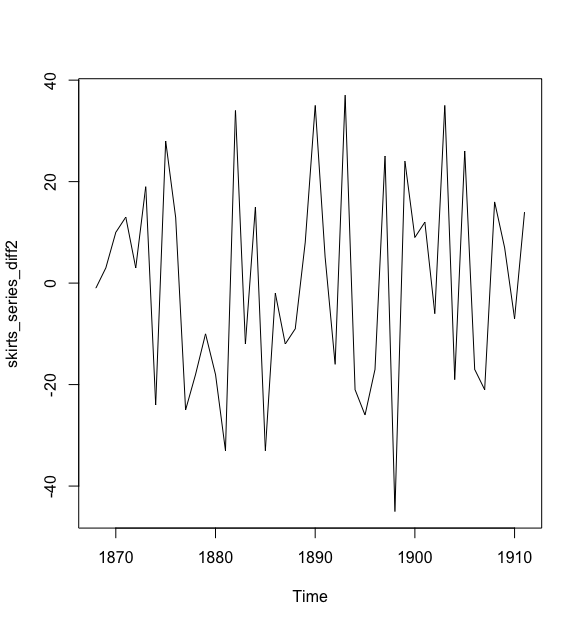
二次差分后的时间序列在均值和方差上确实看起来像是平稳的，随着时间推移，时间序列的水平和方差大致保持不变。因此，看起来我们需要对裙子直径进行两次差分以得到平稳的时间序列.

对平稳性正式的检验我们会在后面理论章节介绍

选择一个合适的ARIMA模型

如果你的时间序列是平稳的，或者你通过n次差分转化我一个平稳时间序列，接下来就是要选择合适的ARIMA模型，这意外着需要寻找ARIMA(p,d,q)中合适的p值和q值。为了得到这些，通常需要检查平稳时间序列的自相关图和偏自相关图.

我们使用R中的acf()和pacf()函数来分别查看自相关图和偏自相关图。在acf()和pacf()设定plot=FALSE来得到自相关和偏自相关的真实值.

例如，以英国国王去世年龄的一阶差分序列滞后1-20阶数(lags 1-20)的相关图，并且得到其自相关系数

#一阶差分，得到平稳时间序列
> kings_timeseries_diff1 <- diff(kings_timeseries, differences = 1)

#画出自相关图
> acf(kings_timeseries_diff1, lag.max = 20)

#查看真实的自相关系数
> acf(kings_timeseries_diff1, lag.max = 20, plot = FALSE)

Autocorrelations of series ‘kings_timeseries_diff1’, by lag

     0      1      2      3      4      5      6      7      8      9     10 
 1.000 -0.360 -0.162 -0.050  0.227 -0.042 -0.181  0.095  0.064 -0.116 -0.071 
    11     12     13     14     15     16     17     18     19     20 
 0.206 -0.017 -0.212  0.130  0.114 -0.009 -0.192  0.072  0.113 -0.093 
> 

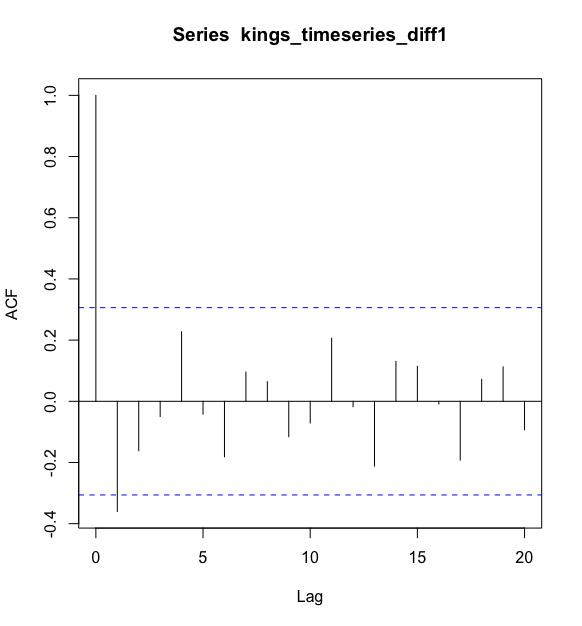
从相关图中可以看出，在滞后1阶的自相关值(-0.360)超出了置信边界，但是其他所有在滞后1-20阶的自相关值都没有超出置信边界.

要画出英国国王去世年龄在滞后1-20阶一阶差分时间序列的偏自相关图，并得到偏相关的值，我们使用pacf()函数:

#画出偏自相关图
> pacf(kings_timeseries_diff1, lag.max = 20)

#偏自相关系数的真实值
> pacf(kings_timeseries_diff1, lag.max = 20, plot = FALSE)

Partial autocorrelations of series ‘kings_timeseries_diff1’, by lag

     1      2      3      4      5      6      7      8      9     10     11 
-0.360 -0.335 -0.321  0.005  0.025 -0.144 -0.022 -0.007 -0.143 -0.167  0.065 
    12     13     14     15     16     17     18     19     20 
 0.034 -0.161  0.036  0.066  0.081 -0.005 -0.027 -0.006 -0.037 
>

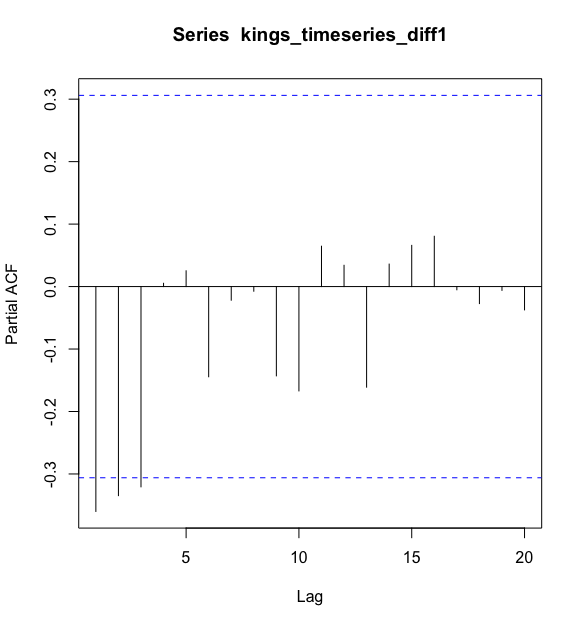
偏相关图显示在滞后1,2和3阶(lags 1,2,3)时的偏自相关系数超过了置信边界，为负值，且在等级上随着滞后阶数的增加而缓慢减少(lag1: -0.360, lag 2: -0.335, lag 3: -0.321)。从lag 3滞后偏自相关系数值缩小至0.

既然自相关值在滞后1阶(lags 1)之后为0，且偏相关值在滞后3阶(lags 3)之后缩小至0，那么意味着接下来的ARIMA模型对于一阶时间序列有如下性质:

1. ARMA(3,0)模型：即偏自相关值在滞后3阶(lags 3)滞后缩小至0，则是一个阶层p=3的自回归模型.

2. ARMA(0,1)模型：即自相关图在滞后1阶(lags 1)之后为0且偏自相关图缩小至0，则是一个阶数q=1的移动平均模型.

3. ARMA(p,q)模型：即自相关图和偏自相关图都缩小至0，则是一个具有p和q大于0的混合模型.

我们利用简单的原则来确定哪个模型是最好的：即我们认为具有最少参数的模型是最好的。显然ARMA(0,1)只有1个参数，被认为是最好的模型.

ARMA(0,1)模型是一阶的移动平均模型，或者称为MA(1).

auto.arima()函数可以用来自动发现合适的ARIMA模型，例如输入library(forecast)，然后auto.arima(kings)，那么输出合适的模型是ARIMA(0,1,1)。

不过这个函数有时候不总是有效的，需要结合实际情况来分析.

使用ARIMA模型进行预测

一旦你为你的时间序列数据选择了最好的ARIMA(p,d,q)模型，你可以估计ARIMA模型的参数，并使用它们做出预测模型来对你的时间序列中的未来值进行预测.

你可以使用arima()函数来估计ARIMA(p,d,q)模型中的参数.

例如，英国国王去世年龄的例子，使用ARIMA(0,1,1)

#对ARIMA(0,1,1)模型进行参数估计
> kings_timeseries_arima <- arima(kings_timeseries, order = c(0,1,1))

> kings_timeseries_arima

Call:
arima(x = kings_timeseries, order = c(0, 1, 1))

Coefficients:
          ma1
      -0.7218
s.e.   0.1208

sigma^2 estimated as 230.4:  log likelihood = -170.06,  aic = 344.13
>

上面提到，我们对时间序列使用ARIMA(0,1,1)模型，就意味着对一阶差分时间序列使用了ARMA(0,1)模型，该模型可以写作$X_t - \mu = Z_t - (\theta * Z_t - 1)$，其中$\theta$是被估计的参数，如此例中，$\theta$的估计值由ma1给出，为-0.7218

指定预测区间的置信水平

有了模型后，我们就可以用该模型来进行预测了。可以使用forecast()函数中的level参数来确定预测区间的置信水平。

例如，为了得到99.5%的预测区间，我们可以使用forecast(kings_timeseries_arima, h = 5, level = c(99.5))

#使用默认参数，对时间序列预测未来5个国王去世年龄
> kings_timeseries_forecasts <- forecast(kings_timeseries_arima, h = 5)

> kings_timeseries_forecasts
   Point Forecast    Lo 80    Hi 80    Lo 95     Hi 95
43       67.75063 48.29647 87.20479 37.99806  97.50319
44       67.75063 47.55748 87.94377 36.86788  98.63338
45       67.75063 46.84460 88.65665 35.77762  99.72363
46       67.75063 46.15524 89.34601 34.72333 100.77792
47       67.75063 45.48722 90.01404 33.70168 101.79958

#画出预测结果图
> plot(kings_timeseries_forecasts)
> 

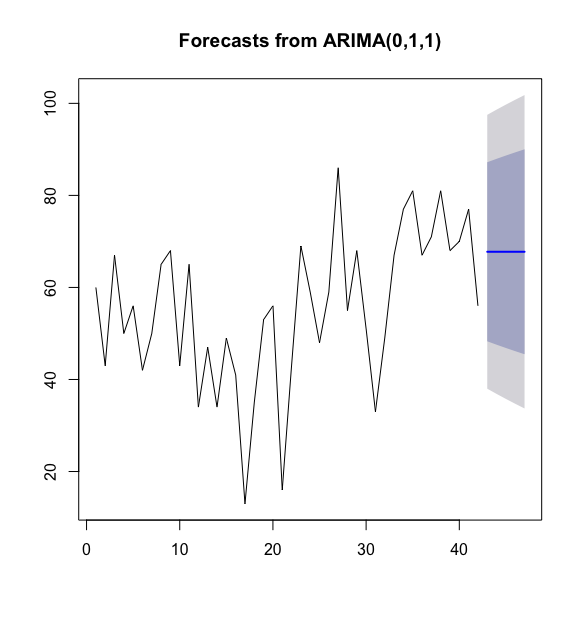
原始时间序列中包括42位英国国王的去世年龄，我们又预测了未来5个国王(国王43-47)的去世年龄，对这些预测的预测区间我们同时设置为80%和95%.

在指数平滑模型下，观察ARIMA模型的预测误差是否是均值为零、方差为常数的正态分布是个好主意，同时也要观察连续预测误差是否自相关.

#查看残差的自相关性
> acf(kings_timeseries_forecasts$residuals, lag.max = 20)

> Box.test(kings_timeseries_forecasts$residuals, lag = 20, type = "Ljung-Box")

    Box-Ljung test

data:  kings_timeseries_forecasts$residuals
X-squared = 13.584, df = 20, p-value = 0.8509

#画出残差图
> plot(kings_timeseries_forecasts$residuals)

> plotForecastErrors(kings_timeseries_forecasts$residuals) 

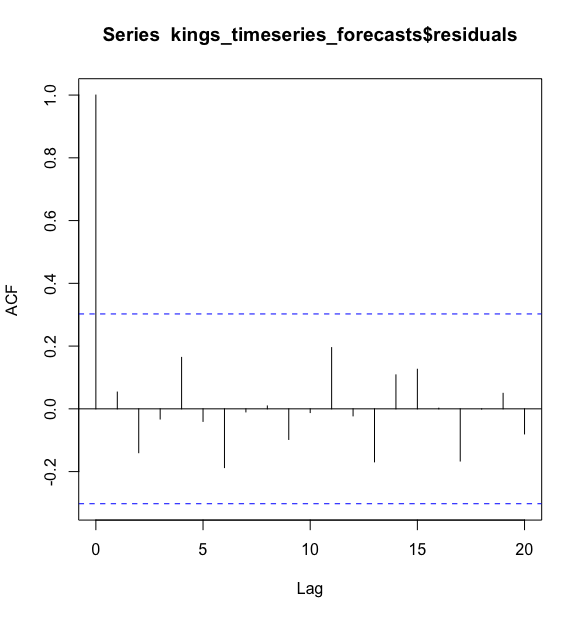
既然相关图显示出在滞后1-20阶(lags 1-20)中样本自相关值都没有超出显著的置信边界，而且Ljung-Box检验的p值为0.9，所以我们推断在滞后1-20阶(lags 1-20)中没有明显证据说明预测误差是非零自相关的.

时间序列的直方图显示预测误差大致是正态分布的，且均值接近于0.因此，把预测误差看作平均值为0方差为常数的正态分布式合理的.

这就说明对于英国国王去世年龄的数据，ARIMA(0,1,1)模型作为预测模型是非常合适的.

本文中提到的关键性词语，我们会在后面讲解理论时逐个解释