机器学习篇

随机森林

随机森林算法是基于决策树的一种集成学习方法，它会生成多棵决策树，生成每棵决策树的时候在分裂属性集和构建数据集上都做了随机扰动，这样能是随机森林具有更稳健的预测结果.

随机森林改进了单棵决策树分类，其本质上还是一棵一棵的决策树，决策树已在上篇详细讲解了，所以本篇不会过多的再去将决策树生成的细节.

我们会重点讲解随机森林在训练数据集的选取和结点分裂时的属性集选取，最后重点介绍随机森林在非平衡数据集上的处理.

决策树分类中存在的问题

虽然分类决策树已经取得了很好的效果，但是不可否认还存在一些问题:

• 局部最优解
  决策树算法在分裂后不进行回溯，这样很容易陷入局部最优解的问题.

• 不能处理连续变量
  为了处理大数据或连续变量的种种改进算法不仅增加了分裂算法的额外开销，而且降低了分类的准确度，对连续字段比较难预测，当类别太多时，错误可能就会快速增长；对于时间序列的数据，需要很多预处理的工作.

• 过度拟合
  在决策树的构建过程中，由于原始数据集中可能混入噪声数据，导致决策树产生过度拟合；尽管可以通过决策树剪枝等方法改善，但过拟合依然是分类问题中无法避免的难题.

为了克服单棵决策树的上述缺点，结合单个分类器组合成多个分类器的思想，一种很自然的想法是生成多棵决策树，这些决策树不需要都有很高的分类精度，但通过投票的形式进行决策，能产生很好的效果.

随机森林相比于单棵决策树，多棵决策树之间存在差异性，直观的看就是每棵决策树都能提取出不同的特征，多棵决策树进过组合，就能考虑更多特征组合的情况，在分类时就更准确.

数据集抽样

随机森林是由多棵决策树组成，如果每棵决策树都是用相同的数据集，那得到的每棵决策树差异性就不大，则整个随机森林最后的分类就达不到效果.

我们的做法是如果要构建 $N$ 棵决策树，就在原数据集中抽样产生对应数量的训练集。现有的统计抽样技术有很多，按照抽样是否放回主要包括以下两种:

• 不放回抽样
  设一个总体含有 $N$ 个个体，从中不放回地抽取 $n$ 个个体作为样本 $(n \leq N)$，叫不放回抽样。比如第一次随机抽取 $1$ 个样本后不放回，则还是剩下 $n-1$ 个样本；第二次就从这剩下的 $n-1$ 个样本中再随机抽取 $1$ 个且不放回，则还剩下 $n-2$ 个，依次类推，直到抽取指定数量的样本为止。

  采用不放回抽样的特点是每次抽样时，原数据集的数量会逐渐减少，同时产生的抽样样本不会重复.

• 有放回抽样
  有放回抽样即在抽取样本时，采用抽取后再将抽取的结果放回样本集中的抽样方法；这样每次抽样时数据集的大小不变，但是在抽取的样本集中会出现重复样本的情况.

---

在有放回抽样中，根据抽样时是否设置权重又分为无权抽样和有权重抽样:

• 无权重抽样
  也叫 bagging 方法，是一种用来提高学习算法准确度的方法。bagging 法是以可重复的随机抽样为基础，每个样本是初始数据集有放回抽样，且每个样本的权重相同.

  在可重复抽样生成多个训练子集时，存在于初始训练集 $D$ 中的所有的样本都有被抽取的可能，但在重复多次后，总有一些样本是不能被抽取到的，每个样本不能被抽取的概率为 $\left( 1 - \frac{1}{N} \right)^N$，这里 $N$ 表示原始训练集中样本的个数.

• 更新权重抽样
  也叫 boosting方法，该方法进行抽样时，首先随机抽样产生一组训练集，然后对这组训练集中的每一个训练集设定权重为 $\frac{1}{n}$，$n$ 为训练集中样本的个数，在设定权重后，对每个带权重的训练集进行测试，在每次测试结束后，对分类性能差的训练集的权重进行提升，从而产生一个新的权重系数，进过多次训练后，每个训练集就有一个和其相对应的权重，在投票时，这些权重就可以对投票的结果产生影响，从而影响最终的决策结果.

  著名的 AdaBoost提升算法就是 boosting方法的经典应用，后续篇章中我们会详细讲解该算法.

Bagging方法与 Boosting方法都是可放回的抽样方法，但两者间存在很大的区别：

• Bagging方法在训练的过程中采用独立随机的方式，而 Boosting方法在训练的过程中，每一次训练都是在前一次的基础上进行的，因此是串行的关系，这对算法的执行过程是一个很大的挑战，因为每一次执行都要等上一次执行完成才能继续，所以无法使用并行处理的方式来计算

• Bagging方法抽取出来的训练集都是没有权重的，而 Boosting方法在抽取过程中，对每个训练集都设定权重，使得抽取结束后，每个训练集的待遇是不一致的.

随机森林算法主要采用 bagging抽样技术，从原始训练集中产生 $N$ 个训练子集，每个训练子集的大小约为原始训练集的 $\frac{2}{3}$，每次抽样均为随机且放回抽样，这样使得训练子集中的样本存在一定的重复，这样做的目的是为了使森林中的决策树不至于产生局部最优解.

随机森林

随机森林本质上就是多生成几棵决策树，然后众多决策树对预测结果进行投票，决定最后的分类结果。

下面简要描述一下整个过程:

1. 假设原始训练集为 $N$，应用 bootstrap 法 有放回地随机抽取 $k$ 个新的样本作为自助样本集，并以此自助样本集构建一棵决策树.

   循环迭代 $t$ 次，这样就能构建 $t$ 棵决策树，构成随机森林.

2. 设每个样本有 $m_{all}$ 个变量，则在每棵树的每个节点处随机抽取 $m_{try}$ 个变量（$m_{try} < m_{all}$），然后在这 $m_{try}$ 个变量中做最优划分属性的选择，并对节点进行分裂.

3. 每棵树最大限度的生长，不做任何剪枝.

4. 将生成的多棵决策树组成随机森林，用随机森林分类器对新的数据进行判别与分类，分类结果按树分类器的投票多少而定.

其中，参数 $k,t,m_{try}$ 都需要事先人为指定，实际应用中，可以通过调整这几个参数来对最后的随机森林模型进行调优。

对节点进行分裂时，最优划分属性的选择和分裂，与决策树的生成一致.

非平衡数据集的处理

非平衡数据概述

非平衡数据是指数据集中某一类样本的数量明显少于其他类样本的数量。在二分类数据集中，我们一般称多数类为正类，少数类为负类.

非平衡数据集会使得负类的预测准确度远远低于正类，使得分类算法得到的分类器具有很大的偏向性，导致分类器的性能大幅度下降.

在实际应用中，非平衡数据是经常存在的，比如网络安全中不安全或恶意的数据信息所占的份额很小，邮件处理中垃圾邮件相对于正常邮件来说数据量很小.

非平衡数据集分类困难的原因分析

数据集非平衡可分为两种:

• 本质非平衡数据集
  指原始数据集由于自身的分布存在不平衡，导致样本中负类非平衡.

  比如对信用卡非法交易的检测，非法交易记录是检测的目标，但训练样本中包含大量正常的信用卡交易记录，只有特别少的一部分属于非法交易.

• 非本质非平衡数据集
  这类主要是人为因素导致的，而不是数据集本身的问题。

  比如数据采集时，由于某些数据获得比较困难或费用比较昂贵，或者是人们出于对个人隐私的考虑而不愿意透露给调查者.

---

数据稀少问题

在非平衡数据集的定义中，负类样本的数据较正类样本稀少得多，这是导致分类器性能急剧下降的最直接原因。

负类样本比正类样本稀少又分为相对数量稀少和绝对数量稀少:

• 相对数量稀少
  非平衡数据集中，被关注的负类样本的绝对数量不少，而由于正例样本非常多，负类样本相对于正例样本的比例过小。

  这种不平衡相对来说比较好处理，可以通过改变训练集规模，或者改变抽样的方法，就可以消除这种不平衡现象，比如欠抽样；而且只要总样本足够多，相对数量较少并不一定会导致分类性能下降。

• 绝对数量稀少
  非平衡数据集中，被关注的负类样本的数量本身很少，从而使得在训练分类器时，负类样本的特征无法完整地在的被训练，导致分类器在预测和分类时效果不好。

  这类可以通过 SMOTE插值法，或者重复抽样的方式来缓解。SMOTE插值法下面会详细讲解。

---

数据碎片问题

数据碎片是指在算法的执行过程中，原来的数据集被划分成多个小的数据集，这些小的数据集的样本量越小，使得原本平衡的数据集变成了非平衡的数据集。

这种现象在决策树和随机森林算法中普遍存在，但这是算法本身引发的问题，目前也没有什么好的解决方案。

还有一些比如噪声数据导致数据非平衡，或者评价指标选择有问题导致数据非平衡等等，感兴趣的读者可以自行查阅相关文献进行学习.

---

非平衡数据集分类问题的解决办法

解决非平衡数据集分类，主要从两个方面去考虑：一是改进算法，二是改造数据。

下面我们主要讨论的是如何来改造数据；改造数据的主要思路是改变训练集数据的分布，通过人为增加负类样本（这些新增的样本称为“人造”样本），提升不平衡率，主要包括随机向上抽样，随机向下抽样，或者是对这两种抽样方法的改进抽样方法。

---

随机上采样和随机下采样

随机上采样就是通过简单的随机复制一批少数类，从而使少数类的数量增加。

随机下采样则是将数据集中的正类样本进行一定程度的删除，从而使得正负例样本的数量得到平衡。

这两种方式都可以使数据达到一定的平衡，但是由于其随机性，使得新的数据集不能很好的代表原始数据集，而且两者间的差异越来越大，经过实践检验，这两种方法都达不到理想的效果。

---

SMOTE算法

针对向上抽样时过于随机性的问题，2002年 Chawla 等人提出了 SMOTE算法(Synthetic Minority Over-samplingTechnique 算法)，该算法的本质是对随机上抽样策略的改进。

SMOTE 算法提出了一种基本假设：相距较近的负类之间的样本任然是负类。从这个假设出发，该方法为每个负类样本确定其 $K$ 个相距最近的负类，然后在样本与其近邻样本的连线上合成“人造”样本，合成过程依据如下公式完成：

$$P_j = x_i + rand(0,1) \times (y_{ij} - x_i)$$ 其中:
$x_i , i = 1,2,\cdots,n$ 为负类样本，$n$ 为负类样本总个数；
$y_{ij},j = 1,2,\cdots,m$ 为 $x_i$ 相邻的 $m$ 个近邻样本；
$p_j , j = 1,2,\cdots,m$ 为合成的“人造”样本；
$rand(0,1)$ 表示在 $(0,1)$ 之间的一个随机数.

通过这种组合产生的“人造”样本就具有一些简单复制样本不能具备的优良特性，比如“人造”样本不会和原数据集中的样本重合，“人造”样本继承了负类样本和相邻样本的某些特性。

把这些“人造”的负类样本加入到初始的非平衡数据集中，生成的新的数据集的非平衡性就大大降低了，且可以较好地提升分类算法在非平衡数据集上的性能。

---

该算法的执行步骤为：

1. 为每个负类样本挑选出 $K$ 个数量的邻近样本；
2. 将负类样本和其邻近样本进行线性组合；
3. 将组合产生的新的“人造”样本加入到原数据集中；
4. 计算数据集的非平衡率，当数据集没有达到目标平衡率时，转第一步重复迭代，否则程序结束；

其中，程序结束的指标为非平衡率，它是少数类占全体样本量的比率；不平衡率越小说明该数据集的不平衡程度越严重。参数 $K$ 由使用者根据实际情况设定。

---

SMOTE算法的缺点：

除了参数 $K$ 需要人为根据经验设定外，该算法无法克服非平衡数据集的数据分布问题，容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻，如果一个负类样本处在负类样本集的分布边缘，则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘，且会越来越边缘化，从而模糊了正类样本和负类样本的边界。

有一些人提出了改进方法，比如先将负类样本进行聚类，然后选择聚类中心的 $k$近邻，然后对每个近邻再应用 SMOTE算法，这样可以解决分布边缘化问题。

---

R 示例演示

我们以 iris（鸾尾花）的数据集作为样本集来演示随机森林的训练和分类；

R 中要的随机森林包为 randomForest，如果没有安装该包的读者，需要先安装包，如下:

# 安装包
> install.packages("randomForest")

在每次程序运行时，都需要加载该包到工作空间中:

# 加载包
> library(randomForest)

导包成功后我们开始分析，先要构造出训练数据集和测试数据集:

# 导入 irirs 数据集到工作区中
> data("iris")
# 我们先查看该数据集有哪些字段
> head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa
> 
# 下面将数据集按 80%,20% 的比例拆分为训练集和测试集
> set.seed(100)
> ind = sample(2,nrow(iris),replace = TRUE,prob = c(0.8,0.2))
> trainset = iris[ind == 1,]
> testset = iris[ind == 2,]
>

从数据集的字段显示看成，该数据集的每条记录分别有五个字段，Sepal.Length , Sepal.Width 为花萼的长和宽，Petal.Length , Petal.Width 为花瓣的长和宽，这四个为分类变量，用于分类；Species 为花的种类，为输出变量，有几种类别，用于标号.

到这一步训练样本和测试样本就构造好了，下面开始训练随机森林模型:

# 应用随机森林模型来训练训练数据集
> iris.rf = randomForest(Species ~.,trainset,ntree = 50,nPerm = 10,mtry = 3,proximity = TRUE,importance = TRUE)
# 查看训练好的随机森林模型
> print(iris.rf)
Call:
 randomForest(formula = Species ~ ., data = trainset, ntree = 50,      nPerm = 10, mtry = 3, proximity = TRUE, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 50
No. of variables tried at each split: 3
        OOB estimate of  error rate: 3.31%
Confusion matrix:
           setosa versicolor virginica class.error
setosa         40          0         0  0.00000000
versicolor      0         40         2  0.04761905
virginica       0          2        37  0.05128205
> 

对randomForest()函数进行说明:
Species ~ . : 代表预测的模式，表示以训练集trainset中除了 Species变量的其他所有变量来生成随机森林，预测出Species变量.

ntree = 50 : 表示要生成 50 棵决策树，构成随机森林.

nperm：计算importance时的重复次数

mtry：选择的分裂属性的个数

proximity=TRUE：表示生成临近矩阵

importance=TRUE：输出分裂属性的重要性

对该函数其他细节可以查看帮助文档 help("randomForest")

我们还可以输出训练的随机森林模型的均方差图来看:

> plot(iris.rf)
> 

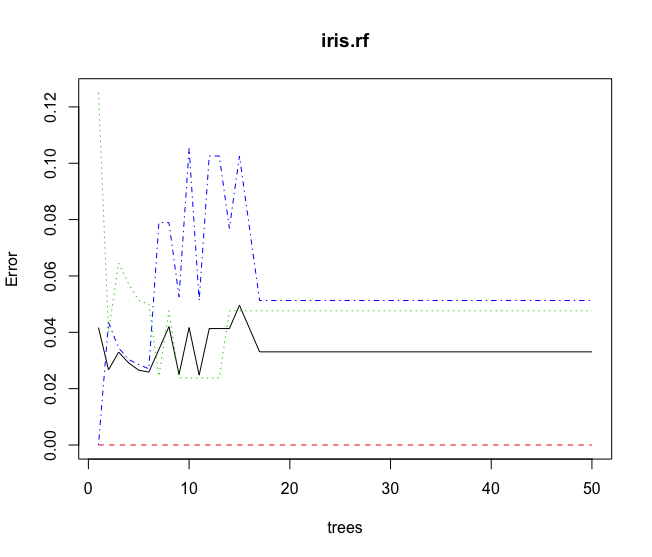
从图中看成，随着随机森林中决策树的数目越来越多后，均方误差会趋于平稳，说明在构建 20 棵决策树后，随机森林模型已经稳健了.据此，我们可以在后面调参时，减小生成的决策树的数量，加快模型的训练速度.

训练好模型后，下面演示如何使用模型进行预测:

# 对测试集进行 预测
> iris.pred = predict(iris.rf,testset)
# 输出预测测试集的 混淆矩阵
> iris.table = table(observed = testset[,"Species"],predicted = iris.pred)
>

或者我们可以通过 caret包的相关函数输出完整的混淆矩阵信息:

# 需要导入 caret包
> library(caret)
# 输出完整的混淆矩阵信息
> confusionMatrix(iris.table)
Confusion Matrix and Statistics
            predicted
observed     setosa versicolor virginica
  setosa         10          0         0
  versicolor      0          7         1
  virginica       0          2         9
Overall Statistics
               Accuracy : 0.8966          
                 95% CI : (0.7265, 0.9781)
    No Information Rate : 0.3448          
    P-Value [Acc > NIR] : 1.035e-09       
                  Kappa : 0.8444          
 Mcnemar's Test P-Value : NA              
Statistics by Class:
                     Class: setosa Class: versicolor Class: virginica
Sensitivity                 1.0000            0.7778           0.9000
Specificity                 1.0000            0.9500           0.8947
Pos Pred Value              1.0000            0.8750           0.8182
Neg Pred Value              1.0000            0.9048           0.9444
Prevalence                  0.3448            0.3103           0.3448
Detection Rate              0.3448            0.2414           0.3103
Detection Prevalence        0.3448            0.2759           0.3793
Balanced Accuracy           1.0000            0.8639           0.8974
> 

从输出的 Accuracy : 0.8966 中我们可知，此随机森林的预测精确度为 89.66%

小结

到这里，整个随机森林算法就讲解完了.