机器学习篇

决策树

决策树在逻辑上是树形结构，主要是为了解决分类问题，所谓决策树的分类就是从根节点开始，根据其测试属性依次往其子节点逐步细分的过程.

它是最直观的分类算法，也是最容易理解的算法之一.

决策树的形象实例

在讲解理论逻辑之前，先讲一个网友给出了一个"女儿相亲"的例子，让读者先体会一下什么是决策分类.

现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

女儿：多大年纪了？
母亲：26。
女儿：长的帅不帅？
母亲：挺帅的。
女儿：收入高不？
母亲：不算很高，中等情况。
女儿：是公务员不？
母亲：是，在税务局上班呢。
女儿：那好，我去见见。

这个女孩的决策过程就是典型的分类树决策。

相当于通过年龄、长相、收入和是否公务员对男人分为两个类别：见和不见。

假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑:

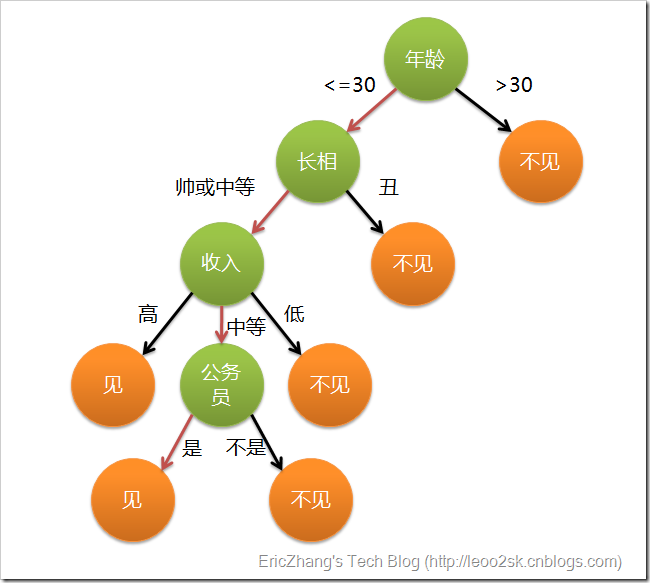
上图完整表达了这个女孩决定是否见一个约会对象的策略，其中绿色节点表示判断条件，橙色节点表示决策结果，箭头表示在一个判断条件在不同情况下的决策路径，图中红色箭头表示了上面例子中女孩的决策过程。

这幅图基本可以算是一颗决策树，说它“基本可以算”是因为图中的判定条件没有量化，如收入高中低等等，还不能算是严格意义上的决策树，如果将所有条件量化，则就变成真正的决策树了。

---

决策树算法描述

有了上面直观的认识，我们可以正式定义决策树了：

决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。

其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。

使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单且直观的“分而治之”（divide-and-conquer）策略.

---

具体算法步骤如下：

输入:
训练集 $D = \{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\cdots,(\boldsymbol{x}_m,y_m)\}$
属性集 $A = \{ a_1,a_2,\cdots,a_d \}$

过程: 函数 $TreeGenerate(D,A)$
1. 生成结点 node
2. $if \quad$ $D$中样本全属于同一类别$C$ $\quad then$
3. $\qquad$将 node 标记为 $C$类叶结点; $\quad return$
4. $end \quad if$
5. $if \quad A = \emptyset \ \ OR \ \ D$ 中样本在 $A$ 上取值相同 $\quad then$
6. $\qquad$ 将 node 标记为叶结点，其类别标记为 $D$ 中样本数最多的类; $\quad return$
7. $end \quad if$
8. 从 $A$ 中选择最优划分属性 $a_*$;
9. $for \quad a_* \ 的每一个值 \ a_*^v \quad do$
10. $\qquad$ 为 node 生成一个分支;令 $D_v$ 表示 $D$中在 $a_*$ 上取值为 $a_*^v$ 的样本子集;
11. $\qquad \ if \quad D_v \ 为空 \quad then$
12. $\qquad \qquad$ 将分支结点标记为叶结点，其类别标记为 $D$ 中样本最多的类; $\quad return$
13. $\qquad else$
14. $\qquad \qquad$ 以 $TreeGenerate(D_v,A \setminus \{ a_* \})$ 为分支结点
15. $\qquad end \quad if$
16. $end \quad for$

输出: 以 node 为根结点的一棵决策树

---

显然，决策树的生成是一个递归过程.在决策树基本算法中，有三种情形会导致递归返回:

1. 当前结点包含的样本全属于同一类别，无需划分
2. 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分
3. 当前结点包含的样本集合为空，不能划分

在第 2 种情形下，我们把当前结点标记为叶结点，并将其类别设定为该结点所含样本最多的类别;

在第 3 种情形下，同样把当前结点标记为叶结点，但将其类别设定为其父结点所含样本最多的类别;

---

划分选择

从上面的算法过程可以看出，决策树学习的关键是第 8 行，即如何选择最优划分属性.

一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”（purity）越来越高.

根据划分算法的不同，决策树算法的名称也就不同了，下面分布介绍一些划分算法.

信息熵

“信息熵”（information entropy）表示的是一种混乱程度，是度量样本集合纯度最常用的一种指标，信息熵越大，就越混乱，纯度越低.

假设当前样本集合 $D$ 中第 $k$ 类样本所占的比例为 $p_k (k = 1,2,\cdots,|y|)$，则 $D$ 的信息熵定义为:

$$Ent(D) = - \sum_{k=1}^{|y|} p_k \log_2{p_k}$$ $Ent(D)$ 的值越小，则 $D$ 的纯度越高.

下面的一些划分算法大多都是基于信息熵的，所以先给出信息熵的定义.

---

信息增益

假定离散属性 $a$ 有 $V$ 个可能的取值 $\{ a^1,a^2,\cdots,a^V \}$，若使用 $a$ 来对样本集 $D$ 进行划分，则会产生 $V$ 个分支结点，其中第 $v$ 个分支结点包含了 $D$ 中所有在属性 $a$ 上取值为 $a^v$ 的样本，记为 $D^v$ .

则我们可以计算出 $D^v$ 的信息熵，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权值 $\frac{|D^v|}{|D|}$，即样本数越多的分支结点的影响越大，于是可计算出用属性 $a$ 对样本集 $D$ 进行划分所获得的“信息增益”（information gain）:

$$Gain(D,a) = Ent(D) - \sum_{v=1}^V \frac{|D^v|}{|D|} Ent(D^v)$$ 一般而言，信息增益越大，则意味着使用属性 $a$ 来划分所获得的“纯度提升”越大.

因此，我们可以使用信息增益来进行决策树的划分属性选择，即上述算法步骤中的第 8 行选择属性 $a_* = arg \ \max_{a \in A}{Gain(D,a)}$ .

著名的 ID3决策树学习算法就是使用的信息增益作为划分准则.

为什么选择最大的信息增益属性作为分裂属性呢？这是因为将信息增益最大的属性首先分裂开，对整体而言，得到的“纯度提升”最大，则越快的得到纯的分支.

---

下面用SNS社区中不真实账号检测的例子来说明ID3算法的构造步骤。为了简单起见，我们假设训练集包含 10 个元素:

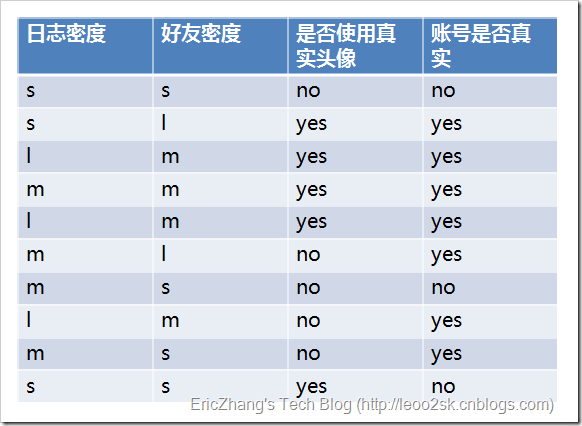
其中，$s,m,l$ 分别表示小、中和大.

设$L,F,H,R$ 分别表示日志密度、好友密度、是否使用真实头像、账号是否真实 这四个属性；下面计算个属性的信息增益:

$$\begin{array} EEnt(D) &=& -0.7 \log_2{0.7} - 0.3 \log_2{0.3} \\&=& 0.7*0.51 + 0.3*1.74 = 0.879 \\ Ent(D^L) &=& 0.3*(-\frac{0}{3} \log_2{\frac{0}{3}} - \frac{3}{3} \log_2{\frac{3}{3}}) \\&+& 0.4*(-\frac{1}{4} \log_2{\frac{1}{4}} - \frac{3}{4} \log_2{\frac{3}{4}}) \\&+& 0.3*(-\frac{1}{3} \log_2{\frac{1}{3}} - \frac{2}{3} \log_2{\frac{2}{3}}) \\&=& 0 + 0.326 + 0.277 = 0.603 \\ Gain(L) &=& 0.879 - 0.603 = 0.276 \end{array}$$

因此日志密度的信息增益是 0.276

用同样的方法得到 $H,F$ 的信息增益分别为 0.033 和 0.553

因为 $F$ 具有最大的信息增益，所以第一次分裂选择 $F$ 为分裂属性，分裂后的结果如下图:

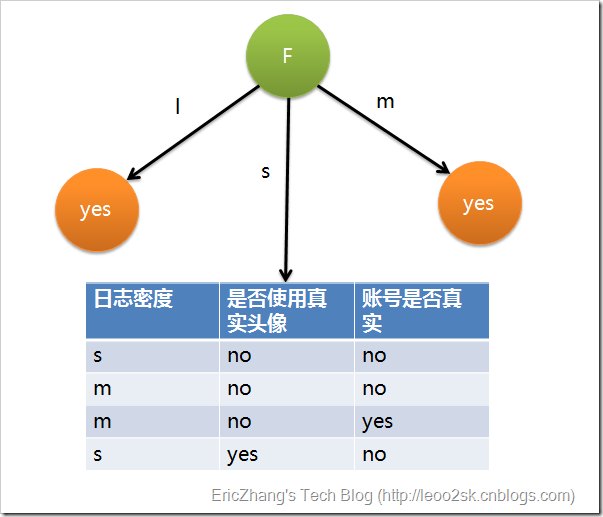
在上图的基础上，再递归使用该方法计算子节点的分裂属性，最终就可以得到整个决策树了.

---

增益率

信息增益有个问题，就是偏向于选择可取值数目较多的属性；可以直观的理解为: 可选值越多，越容易混乱，越混乱的属性越需要先划分开.

为了解决上述问题，人们提出使用“增益率”（gain ratio）来选择最优划分属性；

采用的符号与信息增益时一致，增益率定义为:

$$\begin{array} GGain\_ratio(D,a) &=& \frac{Gain(D,a)}{IV(a)} \\ IV(a) &=& -\sum_{v=1}^V \frac{|D^v|}{|D|} \log_2{\frac{|D^v|}{|D|}} \end{array}$$ 称为属性 $a$ 的“固有值”（intrinsic value）.属性 $a$ 的可能取值数目越多（即 $V$ 越大），则 $IV(a)$ 的值通常会越大.

著名的 C4.5决策树算法就是使用的信息增益作为划分准则.

需要注意的是，增益率准则又对可取值数目较少的属性有所偏好，因此C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用一个启发式: 先从候选划分属性中找出信息增益高于平均水平的属性，再从选择增益率最高的.

---

基尼指数

数据集 $D$ 的纯度可用基尼值来度量:

$$Gini(D) = \sum_{k=1}^{|y|} \sum_{k' \neq k} p_k p_{k'} = 1 - \sum_{k=1}^{|y|} p_k^2$$ 其中 $p_k$表示第 $k$ 类样本所占的比例.

直观来说，$Gini(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率.因此，$Gini(D)$ 越小，则数据集 $D$ 的纯度越高.

---

则属性 $a$ 的基尼指数定义为:

$$Gini\_index(D,a) = \sum_{v=1}^V \frac{|D^v|}{|D|} Gini(D^v)$$ 于是，我们在候选属性集合 $A$ 中，选择那个使得划分后基尼指数最小的属性作为划分属性，即 $a_* = arg \ min_{a \in A} Gini\_index(D,a)$

著名的 CART决策树算法就是使用的基尼指数作为划分准则.

---

剪枝处理

剪枝（pruning）是决策树学习算法对付“过拟合”的主要手段.在决策树学习中，为了尽可能正确分类训练样本，节点划分过程将不断重复，有时会造成决策树分支过多，这时就可能因训练样本学习的“太好”了，以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合.因此，可通过主动去掉一些分支来降低过拟合的风险.

根据剪枝所出现的时间点不同，分为预剪枝和后剪枝。预剪枝是在决策树的生成过程中进行的；后剪枝是在决策树生成之后进行的.

Reduced Error Pruning: 误差降低剪枝

最简单粗暴的一种后剪枝方法，其目的是减少误差样本的数量：

$$\begin{array} ff(T) &=& -\sum_{t \in T} e(t) \\ f(T') &=& -\sum_{t \in T'} e(t) \end{array}$$ 其中，$T$ 表示当前树的节点，$T'$表示去掉某个节点 $N$ 之后的树的节点；$e(t)$ 表示某个节点下的训练样本点误判数量。

剪枝条件 : $f(T) \leq f(T')$，即 $e(t_{K'}) \leq e(t_K)$

---

Pessimistic Error Pruning: 悲观错误剪枝

该方法基于训练数据的误差评估，因此不用单独找剪枝数据集。但训练数据也带来错分误差偏向于训练集，因此需要加入修正 $\frac{1}{2}$。是自上而下的修剪。

具有 $T$ 个节点的树的误差率表示为 :

$$E(T) = \sum_{t \in T} \frac{e(t) + \frac{1}{2}}{N(t)}$$ 去掉节点 $K'$ 之后 $T'$ 个节点的树的误差表示为 : $$E(T') = \sum_{t \in T/K} \frac{e(t) + \frac{1}{2}}{N(t)}$$ 其中，$e(t)$ 表示节点 $t$ 下的训练集的误判个数，$N(t)$ 表示节点 $t$ 下的训练集的总个数.

若设 $n(t) = \frac{e(t) + \frac{1}{2}}{N(t)}$，则可以证明

$$E(T') - E(T) = n(t_K') - n(t_K) = \frac{e(t_{K'}) - e(t_K)}{N(t)}$$ 即带着某个点的分支的判断误差 减去 去掉该点后该分支的误判个数，再除以该分支的总个数.

剪枝条件 :

$$SE(n(t_{K'})) = \sqrt{\frac{n(t_{K'}) * (N(t) - n(t_{K'}))}{N(t)}} \leq E(T') - E(T) = \frac{e(t_{K'}) - e(t_K)}{N(t)}$$

---

Minimum Error Pruning: 最小误差剪枝

待补充......

Cost-Complexity Pruning: 代价复杂剪枝

该方法在Breiman1984年的经典 CART算法 中首次提到并使用。

CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小（模型变简单），从而能够对未知数据有更准确的预测。

CART剪枝算法由两步组成：首先从生成算法产生的决策树 $T_0$ 底端开始不断剪枝，直到 $T_0$ 的根结点，形成一个子树序列 $\{T_0,T_1,\cdots,T_n\}$；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树。

---

先给出决策树的损失函数公式:

$$C_{\alpha} = \sum_{t = 1}^{|T|} N_tH_t(T) + \alpha |T|$$ 其中，$N_tH_t(T)$ 表示事物的不确定性次数，$|T|$表示该树的复杂度，$\alpha$是一个人为设定的已知的参数.

如何来理解这个损失函数，首先什么是事物的不确定度？

最开始时训练集就是一堆数据，只知道标号，以最上面相亲的例子来说明就是：只知道对方是男的，而对其他属性毫无所知，所以这种情况下去相亲代价是最大的，因为不确定性最大，从数学角度来说就是混乱程度最大（或者是信息熵最大）；而后面通过一步步询问其属性，最后才确定是否去相亲，这一步就是逐渐根据属性挖掘出规则，得到更多集合的信息，这样使得训练集的不确定度逐渐降低。

随着不确定性逐渐降低，决策树做出的决策也会更准确，但是模型也会更复杂，因为决策树的规则变复杂了。当数据集中存在噪声时，由于过度追求集合不确定性的减少，而导致模型变得很复杂，以至于发生“过拟合”，过拟合会将训练集上的个例特征当做通用特征，从而使模型在训练集上分类结果很好，而在测试集上分类效果很差.

所以上述 $C_{\alpha}$ 的构造 就是为了在不确定性和模型复杂性之间找到一个平衡点，从而是模型在保证准确率的条件下，模型又不至于过拟合.

---

决策树学习的过程，就是让损失函数逐步减小的过程。从损失函数的表达式上看，要想减小损失函数，有两种办法:

• 降低第一部分的不确定次数，但我们知道这是不可能的了，因为降低不确定次数的办法是再找寻一个特征，或者找寻特征的最优切分点。这在生成决策时就已经决定了，无法改变。
• 进行剪枝操作，这是可以的。剪枝最明显地变化就是叶结点个数变少。假设是一个三叉树，那么一次剪枝它的叶结点数减少 2 个。变化量为 $2\alpha$ ，有了这变化量，我们就可以用来求解最优决策子树了。

同时应该考虑到，剪枝操作虽然使得模型复杂度降低了，但是不确定性却增加了（因为规则变少了），如果模型复杂度降低所带来的提升要小于不确定性增加带来的损失，那就说明这次剪枝操作是失败的。

而模型复杂度降低能带来多少提升量，与参数 $\alpha$ 的大小有直接的关系，所以 $\alpha$ 的设定是个问题。

在上述剪枝过程中，还需要注意一个有趣的问题。对应于每一个参数 $\alpha$，剪枝后的子树是唯一的嘛？个人觉得这是一个最基本的前提假设，在算法中，它提到了一点，给定参数 $\alpha$，找寻损失函数最小的子树 $T_{\alpha}$，也就是说$<\alpha,T_{\alpha}>$是一一对应的! 并不存在一个 $\alpha$ 对应于多个子树。CART剪枝算法中将用到该基本假设。

---

那 $\alpha$ 如何指定呢？

由于 $<\alpha,T_{\alpha}>$ 是一一对应的，所以我们能生成有限个数的子树，记作 $\{ T_0,T_1,\cdots,T_n \}$ ，只要找寻到对应于每一个子树的 $\alpha$ 不就可以了嘛!

将上述损失函数做一下变换 :

$$C_{\alpha}(T) = \sum_{t =1}^{\vert T\vert}N_tH_t(T) + \alpha\vert T\vert = \sum_{t=1}^{\vert T \vert}(N_tH_t(T)+\alpha)$$

所以说，衡量损失函数大小的真正贡献在于每个叶结点，叶结点不确定次数的累加并加个常数 $\alpha$ 就是我们决策树整体的损失函数。

而为了得到树 $T$ 的所有子序列 $\{ T_0,T_1,\cdots,T_n \}$ ，我们需要从底自上，每次只进行一次剪枝操作，那么进行剪枝操作后，该子序列应该是当前参数的最优子树，且应该是根据所剪的那个结点来计算参数 $\alpha$。

我们说了，是通过最优子树来求解参数 $\alpha$，因此，我们先【假设】我们找到了当前的最优子树，且必然发生剪枝。

假设剪枝后需要归并的子结点为 $t$，则以 $t$ 为单节点的损失函数表示为:

$$C_{\alpha}(t) = C(t) + \alpha$$ 其中，$C(t)$ 是归并后的叶结点的不确定性次数.

剪枝前以 $t$ 为根结点的子树 $T_t$ 的损失函数为 :

$$C_{\alpha}(T_t) = C(T_t) + \alpha |T_t|$$ 其中，$C(T_t)$ 是结点 $t$的不确定度，$T_t$为其分支数.

由于是后剪枝，即决策树以及生成了然后再剪枝，所以 $C(T),C(T_t),|T_t|$ 都是已知的，未知的是 $\alpha$

假设 1 : 必然发生剪枝

从中我们便能求得α，为什么？我们来观察下，上述两个式子。

当α=0或者充分小，明显地，不确定次数：

$$C_{\alpha}(T_t) \lt C_{\alpha}(t)$$ 决策树叶结点越多，不确定性越低，不解释。

当增大α时，总有那么一个点，能够使得：

$$C_{\alpha}(T_t) = C_{\alpha}(t)$$ 当继续增大 $\alpha$ 时， $$C_{\alpha}(T_t) \gt C_{\alpha}(t)$$ 不等式反向，所以我们只要取 $\alpha_1 = \frac{C(t)-C(T_t)}{\vert T_t\vert-1}$ 时，当且仅当 $\alpha \ge \alpha_1$ 时，剪枝必然发生。$\alpha$ 必须满足上述条件，否则前提假设将失去意义。所以说，我们通过假设剪枝必然发生就能找到对应的 $\alpha$。可对于任何一个子结点 $t$ 都可以嘛？别忘了第二个假设。

假设 2 : 剪枝发生后，当前决策树是我们的最优子树

每一次剪枝后我们都能计算出一个 $\alpha$，对应于每一个子节点 $t$ 会生成不同的 $\alpha$ ，我们记作 $\alpha(t)$ ，由此得:

$$C_{\alpha}(t) = C(t)+\alpha(t)$$ 剪枝的决策树什么时候最优？对于当前参数 $\alpha(t)$ 而言，能够找到这样的 $t$，使得 $$\min_{t}\{C(t)+\alpha(t)\}$$ 然而在这里为了能够求得 $\alpha$ 的一个序列，貌似直接最小化了 $$\min_{t}(\frac{C(t)-C(T_t)}{\vert T_t\vert-1})$$

找的 $\alpha$ 即找到了子结点 $t$，即完成了剪枝，即找到了最优子树 $T_1$。有了上述的步骤，为了得到决策树 $T_0$ 的所有子序列，直接递归下去，直到根节点即可。在这一过程中，不断地增加 $\alpha$ 的值，产生新的区间。
后面的思路就很简单了，根据生成的子树序列，用测试集去测试这些子树，谁的测试准确率最高，谁就获胜。

还有一些剪枝算法，比如Minimum Error Pruning(最小误差剪枝)，Error-Based Pruning(基于错误的剪枝)等等，读者可以自行搜索学习.

---

连续值和缺失值处理

连续值处理

到目前为止我们仅讨论了基于离散属性来生成决策树.现实学习任务中常会遇到连续属性，比如身高为 1.75m，则有必要讨论如何在决策树学习中使用连续属性.

由于连续属性的可能取值不再有限，因此不能直接根据连续属性的可取值来对结点进行划分.此时，连续属性离散化技术就可应用了。

---

最简单的策略是采用二分法，即:

给定样本集 $D$ 和连续属性 $a$，假定 $a$ 在 $D$ 上出现了 $n$ 个不同的取值（这里需要区分，属性是连续的，比如身高1.75m,1.732m等，属性的取值有无限多种可能，但是给定的样本集是一定的，该属性出现的取值是有限的），将这些值从小到大进行排序，记为 $\{ a^1,a^2,\cdots,a^n \}$，基于划分点 $t$ 可将 $D$ 分为子集 $D_t^-$ 和 $D_t^+$ ，其中 $D_t^-$ 包含那些在属性 $a$ 上取值不大于 $t$ 的样本，而 $D_t^+$ 则包含那些在属性 $a$ 上取值大于 $t$ 的样本.显然，对相邻的属性取值 $a^i$ 与 $a^{i+1}$ 来说，$t$ 在区间 $[a^i,a^{i+1})$ 中取任意值所产生的划分结果相同。因此，对连续属性 $a$，我们可考察包含 $n - 1$ 个元素的候选划分点集合:

$$T_a = \left\{ \frac{a^i + a^{i+1}}{2} | 1 \leq i \leq n - 1 \right\}$$ 即把区间 $[a^i,a^{i+1})$ 的中位点 $\frac{a^i + a^{i+1}}{2}$ 作为候选划分点.然后，我们就可像离散属性值一样来考察这些划分点，选取最优的划分点进行样本集合的划分。

例如，对 $Gain(D,a)$ 稍加改造得:

$$\begin{array} Gain(D,a) &=& \max_{t \in T_a} Gain(D,a,t) \\&=& \max_{t \in T_a} Ent(D) - \sum_{\lambda \in \{ -,+ \}} \frac{|D_t^{\lambda}|}{|D|} Ent(D_t^{\lambda}) \end{array}$$ 其中，$Gain(D,a,t)$ 是样本集 $D$ 基于划分点 $t$ 二分后的信息增益.于是，我们就选择使 $Gain(D,a,t)$ 最大化的划分点.

连续属性也可多分，比如身高，$\leq t_1$ 表示“矮”，$t_1 \leq a \leq t_2$ 表示“一般”，$\geq t_2$ 表示“高”. 而 $t_1,t_2$的选取，可以根据数据分布来选取.

---

缺失值处理

对缺失值的处理要看具体应用场景，这里搜集了下网友提供的一些常见的处理方式.

采用抛弃缺失值

抛弃极少量的缺失值的样本对决策树的创建影响不是太大。但是如果属性缺失值较多或是关键属性值缺失,创建的决策树将是不完全的,同时可能给用户造成知识上的大量错误信息,所以抛弃缺失值一般不采用。只有在数据库具有极少量的缺失值同时缺失值不是关键的属性值时,且为了加快创建决策树的速度,才采用抛弃属性缺失值的方式创建决策树。

补充缺失值

缺失值较少时按照我们上面的补充规则是可行的。但如果数据库的数据较大,缺失值较多(当然,这样获取的数据库在现实中使用的意义已不大,同时在信息获取方面基本不会出现这样的数据库),这样根据填充后的数据库创建的决策树可能和根据正确值创建的决策树有很大变化。

概率化缺失值

对缺失值的样本赋予该属性所有属性值的概率分布,即将缺失值按照其所在属性已知值的相对概率分布来创建决策树。用系数F进行合理的修正计算的信息量,F=数据库中缺失值所在的属性值样本数量去掉缺失值样本数量/数据库中样本数量的总和,即F表示所给属性具有已知值样本的概率。

在选择分裂属性的时候，训练样本存在缺失值，如何处理？

假如你使用 ID3算法，那么选择分类属性时，就要计算所有属性的熵增(信息增益，Gain)。假设10个样本，属性是a,b,c。在计算 a 属性熵时发现，第 10 个样本的 a 属性缺失，那么就把第 10 个样本去掉，前 9 个样本组成新的样本集，在新样本集上按正常方法计算 a 属性的熵增，然后结果乘 0.9（新样本数占原样本数的比例），就是 a 属性最终的熵。

例如，信息增益的计算式推广为 $\begin{array} Gain(D,a) &=& \rho \times Gain(\overline{D},a) \\&=& \rho \times \left( Ent(\overline{D}) - \sum_{v=1}^V \overline{r}_v Ent(\overline{D}^v) \right) \\ Ent(\overline{D}) &=& -\sum_{k=1}^{|y|} \overline{p}_k \log_2{\overline{p}_k} \end{array}$

直观的看，就是让同一个样本以不同的概率（未缺失值样本占总样本的比例）划入到不同的子节点中去.

分类属性选择完成，对训练样本分类，发现属性缺失怎么办？

比如该节点是根据 a 属性划分，但是待分类样本 a 属性缺失，怎么办呢？假设 a 属性离散，有 1,2 两种取值，那么就把该样本分配到两个子节点中去，但是权重由 1 变为相应离散值个数占样本的比例。然后计算错误率的时候，注意，不是每个样本都是权重为 1，存在分数。

直观的看，就是让同一个样本以不同的概率（按属性取值个数平均划分）划入到不同的子节点中去.

训练完成，给测试集样本分类，有缺失值怎么办？

这时候，就不能按比例分配了，因为你必须给该样本一个确定的label，而不是薛定谔的label。这时候根据投票来确定，或者填充缺失值。

根据缺失值左右划分后产生的影响来处理

在xgboost里，在每个结点上都会将对应变量是缺失值的数据往左右分支各导流一次，然后计算两种导流方案对Objective的影响，最后认为对Objective降低更明显的方向（左或者右）就是缺失数据应该流向的方向，在预测时在这个结点上将同样变量有缺失值的数据都导向训练出来的方向。

例如，某个结点上的判断条件是 A>0 ，有些数据是A<=0，有些是A>0，有些数据的A是缺失值。那么算法首先忽略带缺失值的数据，像正常情况下一样将前两种数据分别计算并导流到左子树与右子树，然后

• 将带缺失值的数据导向左子树，计算出这时候模型的 Objective_L；
• 接着将带缺失值的数据导向右子树，计算出这时候模型的 Objective_R；
• 最后比较 Objective_L 和 Objective_R。

假设Objective_L更小，那么在预测时所有变量A是缺失值的数据在这个结点上都会被导向左边，当作 $A<=0$ 处理。

---

决策树框架的理解

回顾上面决策树的构造过程，可以看到核心步骤就是每个结点如何选取最优划分属性，然后生成子结点；根据不同的划分方法，则决策树算法又被命名为不同的名字。

从上面介绍我们知道，划分方法有“信息增益”、“信息增益率”、“基尼指数”等等，其本质上都是分类，使用这些方法来将结点分成两类或多类；决策树学习的过程，就是在每个结点上利用这些方法训练出分类器；

我们知道的分类方法还有很多，比如“SVM”、“神经网络”、“logistic回归”等等，如果将结点选取最优划分属性的过程用 SVM 来做，生成决策树的过程其实就是 SVM二分类扩展到多分类的一种方法；再比如深度学习中经常用到的“Softmax”算法，可看成是用 Logistic回归 来处理结点最优划分属性的选取.

---

我们的思路还可以扩展，本文上面所有讲到的属性划分都是基于单变量的，即每次划分只考虑一个属性，那能不能考虑基于多变量的划分呢，这又该如何理解？

比如有属性集 $\{ x,y \}$，如果每次只考虑一个属性，则得到的最优划分，要么按 $x$ 划分，要么按 $y$ 划分；在图上表示是，要么画一条垂直于 $y$轴的直线，要么画一条垂直于 $x$ 轴的直线，来将数据集划分开；如果数据集的分布情况如下图所示，结果会怎么样呢？

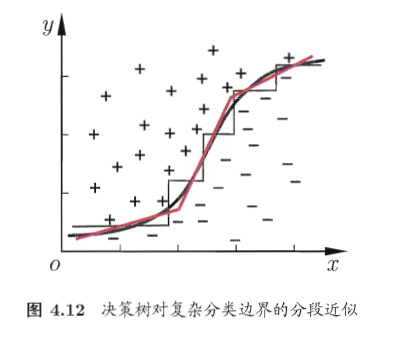
会看到会形成一条复杂的折线，才能将数据集比较好的划分开，也就是生成的决策树会非常复杂。

而如果是每次使用多变量来划分，结果又会如何呢？

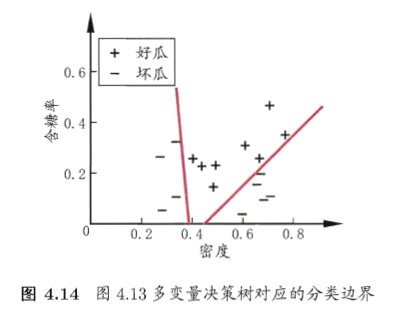
从图中可以看到，多变量划分能产生斜线，能将复杂的数据集快速且简单的划分开.

在考虑多变量的情况下，每个结点训练不同的分类器，那就是考虑诸如“多元线性回归”、“多元非线性回归”等最优划分属性的方法了.

---

再进一步考虑，一个数据集使用不同的最优属性划分方法，可以生成不同的决策树，还有不同的剪枝方法，也可以生成不同的决策树，为了能应用多种算法而产生出更稳健的分类结果，我们可以用不同的决策树算法生成多颗决策树，形成森林，然后基于投票的方法来给数据点进行分类，这就是后面我们要讲的 Random Forest 随机森林.

---

R 程序演示决策树

我们使用 "C50" 包中的 churn数据集来演示决策树的生成与预测；该数据集包含了 3333 个样例，数据维度为 20，19个属性，1个标识，用来判断顾客是否会流失；数据集的介绍可以使用 help("churnTrain")来查看.

数据准备

#如果没有安装 C50 包的先安装包
#install.packages("C50")
> library(C50)
> 
# 加载 churn 数据集
> data(churn)
#查看 数据集的结构
> str(churnTrain)
'data.frame':   3333 obs. of  20 variables:
 $ state                        : Factor w/ 51 levels "AK","AL","AR",..: 17 36 32 36 37 2 20 25 19 50 ...
 ......
 $ voice_mail_plan              : Factor w/ 2 levels "no","yes": 2 2 1 1 1 1 2 1 1 2 ...
 $ number_vmail_messages        : int  25 26 0 0 0 0 24 0 0 37 ...
.......
 $ number_customer_service_calls: int  1 1 0 2 3 0 3 0 1 0 ...
 $ churn                        : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...
> 
# 删除对分类特征不重要的属性
> churnTrain = churnTrain[,!names(churnTrain) %in% c("state","area_code","account_length")]
>

上面删除了三个对分类特征不重要的属性，至于如何判断某个属性对分类是否重要，在后面的文章中讲特征选取时在细讲.

# 使用sample打乱顺序，为保证每次运行结果一致需设置随机种子
> set.seed(2)
> 
# 将 churnTrain的行数分为两部分，第一部分占比 70%，第二部分占比 30%
> ind = sample(2,nrow(churnTrain),replace = TRUE,prob = c(0.7,0.3))
# 第一部分作为训练集
> trainset = churnTrain[ind == 1,]
# 第二部分作为测试集
> testset = churnTrain[ind == 2,]
> dim(trainset)
[1] 2315   17
> dim(testset)
[1] 1018   17
>

生成决策树

这里使用递归分割树来建立分类模型，需要导入 rpart包，如果没有安装此包的读者，先安装包.

#install.packages("rpart")
> library(rpart)
# 在 trainset数据集上用所有的属性生成决策树
> churn.rp = rpart(churn ~.,data = trainset)
> churn.rp
# 检测复杂性参数
> printcp(churn.rp)
# 绘制成本复杂性参数
> plotcp(churn.rp)
# 查看已生成的决策模型
> summary(churn.rp)
# 决策树可视化
> plot(churn.rp,uniform = TRUE,branch = 0.6,margin = 0.1)
> text(churn.rp,all = TRUE,use.n = TRUE)

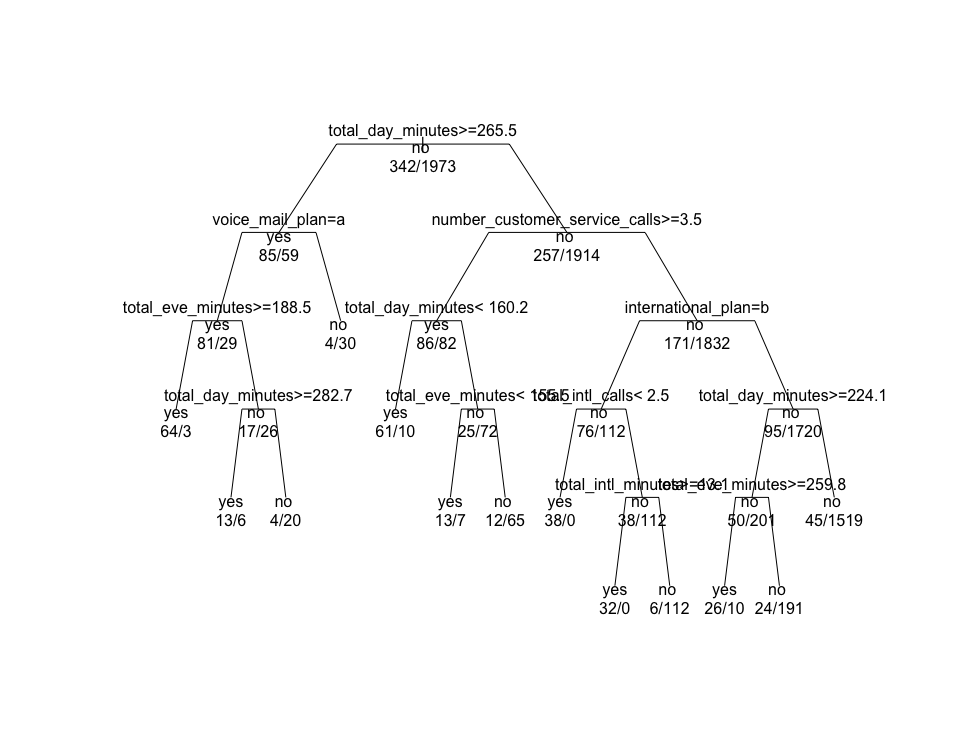
上图就是生成的决策树模型图.

预测

# 对测试集进行预测分类
> predictions = predict(churn.rp,testset,type = "class")
# 与测试集标号对比，建立分类表
> table(testset$churn,predictions)
     predictions
      yes  no
  yes 100  41
  no   18 859
> 
# 为了输出混淆矩阵，需要导入 caret包
> library(caret)
# 输出预测标号与测试标号生成的混淆矩阵
> confusionMatrix(table(predictions,testset$churn))
Confusion Matrix and Statistics
predictions yes  no
        yes 100  18
        no   41 859
               Accuracy : 0.942           
                 95% CI : (0.9259, 0.9556)
    No Information Rate : 0.8615          
    P-Value [Acc > NIR] : < 2.2e-16       
                  Kappa : 0.7393          
 Mcnemar's Test P-Value : 0.004181        
            Sensitivity : 0.70922         
            Specificity : 0.97948         
         Pos Pred Value : 0.84746         
         Neg Pred Value : 0.95444         
             Prevalence : 0.13851         
         Detection Rate : 0.09823         
   Detection Prevalence : 0.11591         
      Balanced Accuracy : 0.84435         
       'Positive' Class : yes             
>

分类表显示，预测有 118例被分为 yes，其中有100例分类正确；900例被分为 no，其中 859例分类正确；

混淆矩阵的输出显示精确度为 0.942，P-Value值很小很小，说明分类效果很好；

决策树剪枝

前面我们已经为 churn 数据集构建了一棵复杂的决策树。但有时候，为了避免过度适应，我们需要去掉一部分分类描述能力比较弱的规则以提高预测正确率。下面介绍使用成本复杂度剪枝方法对分类树剪枝.

# 找到分类树模型的最小交叉检验误差
> min(churn.rp$cptable[,"xerror"])
[1] 0.4707602
# 定位交叉检验误差最小的记录
> which.min(churn.rp$cptable[,"xerror"])
7 
7 
# 获取交叉检验误差最小记录的成本复杂度参数值
> churn.cp = churn.rp$cptable[7,"CP"]
> churn.cp
[1] 0.01754386
> 
# 设置参数 cp 的值与交叉检验误差最小记录的 CP 值相同 来进行剪枝
> prune.tree = prune(churn.rp,cp = churn.cp)
# 绘制分类树
> plot(prune.tree,uniform = TRUE,branch = 0.6,margin = 0.1)
> text(prune.tree,all = TRUE,use.n = TRUE)
>

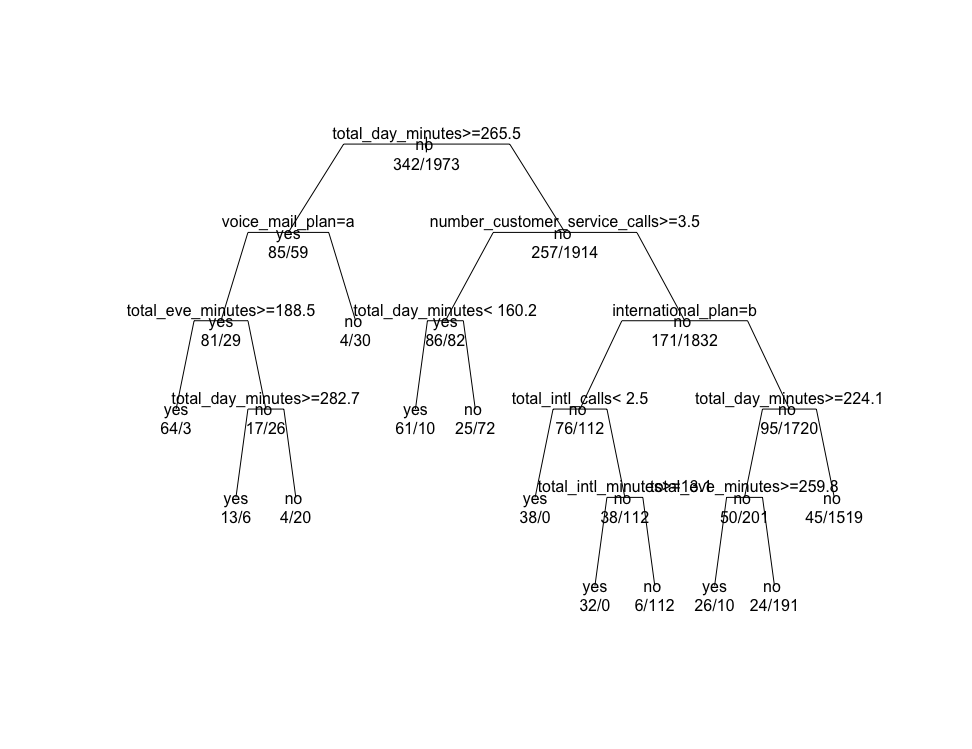
对比剪枝前后的决策树模型图，发现 total_day_minutes < 160.2 的 no 子节点的子树被减掉l.

# 使用剪枝后的决策树进行预测
> predictions = predict(prune.tree,testset,type = "class")
> 
# 考察 此时的混淆矩阵
> confusionMatrix(table(predictions,testset$churn))
Confusion Matrix and Statistics
predictions yes  no
        yes  95  14
        no   46 863
               Accuracy : 0.9411          
                 95% CI : (0.9248, 0.9547)
    No Information Rate : 0.8615          
    P-Value [Acc > NIR] : 2.786e-16       
                  Kappa : 0.727           
 Mcnemar's Test P-Value : 6.279e-05       
            Sensitivity : 0.67376         
            Specificity : 0.98404         
         Pos Pred Value : 0.87156         
         Neg Pred Value : 0.94939         
             Prevalence : 0.13851         
         Detection Rate : 0.09332         
   Detection Prevalence : 0.10707         
      Balanced Accuracy : 0.82890         
       'Positive' Class : yes             
>

对比剪枝前与剪枝后的混淆矩阵中输出的精确度，此例中精确度有点下降；这说明剪枝后不一定能提高准确度，但是剪枝分类树的优势在于它对分类模型的限定更模糊一点，这样可以避免过拟合的问题.

---

也可以调用 party包来构建条件推理树:

library(party)
ctree.model = ctree(churn ~.,data = trainset)
plot(ctree.model)

小结

决策树是一种使用广泛的分类算法，它更多的像是一种算法框架，可以与其他多种算法相结合，比如“SVM”、“Logistic回归”等，所以在构造决策树时，可以先考察数据的分布情况，然后使用何种分类算法.