时间序列篇

残差自回归模型

$ARIMA$模型的提出使人们对非平稳序列的拟合精度大大提高，但和传统的确定性因素分解方法比较，$ARIMA$模型任然有一些缺憾.它使用差分方法提取确定性信息，差分方法的优点是对确定性信息的提取比较充分，缺点是很难对模型进行直观解释.所以当序列具有非常显著的确定性趋势或季节效应时，人们怀恋确定性因素分解方法对各种确定性效应的解释，但又因为它对残差信息的浪费而不敢轻易使用.为了解决这个问题，人们构造了残差自回归(auto-regressive)模型.

模型结构

残差自回归模型的构造思想是首先通过确定性因素分解方法提取序列中主要的确定性信息:

$$x_t = T_t + S_t + \epsilon_t$$
式中，$T_t$为趋势效应拟合；$S_t$ 为季节效应拟合.

考虑到因素分解方法对确定性信息的提取可能不够充分，因而需要进一步检验残差序列 $\{ \epsilon_t \}$ 的自相关性.

如果检验结果显示残差序列的自相关性不显著，说明确定性回归模型对信息的提取比较充分，可以停止分析.如果检验结果显示残差序列的自相关性显著，说明确定性回归模型对信息的提取不充分，这时可以考虑模型对残差序列拟合自回归模型，进一步提取相关信息.

则可构造模型为:

$$\begin{cases} x_t = T_t + S_t + \epsilon_t \\ \epsilon_t = \phi_1 \epsilon_{t-1} + \cdots + \phi_p \epsilon_{t-p} + a_t \\ E(a_t) = 0, Var(a_t) = \sigma^2, Cov(a_t,a_{t-i}) = 0, \forall i \geq 1 \end{cases}$$ 称为（残差）自回归模型(auto-regressive model).

---

实践中，对趋势效应的拟合常用如下两种方式:

1. 自变量为时间 $t$ 的幂函数.

   $$T_t = \beta_0 + \beta_1 \cdot t + \cdots + \beta_k \cdot t^k + \epsilon_t$$

2. 自变量为历史观察值 $\{ x_{t-1}, x_{t-2}, \cdots, x_{t-k} \}$
   

   $$T_t = \beta_0 + \beta_1 \cdot x_{t-1} + \cdots + \beta_k \cdot x_{t-k} + \epsilon_t$$

第二种方式和差分方式的原理相同.

对季节效应的拟合也有两种常用的方式:

1. 给定季节指数.

   $$S_t = S_t'$$ 式中，$S_t'$是某个已知的季节指数.

2. 建立季节自回归模型.

   $$S_t = \alpha_0 + \alpha_1 \cdot x_{t-m} + \cdots + \alpha_l \cdot x_{t-lm}$$ 假定固定周期为 $m$

---

下面以中国农业实际国民收入指数序列来分析:

#读取数据集
> d <- read.table("data/file17.csv",",",header = T)
> x <- ts(d$index,start = 1952)
> t <- c(1:37)
# 拟合关于时间 t 的线性回归模型
> x.fit1 <- lm(x ~ t)
#查看拟合结果
> summary(x.fit1)
Call:
lm(formula = x ~ t)
Residuals:
   Min     1Q Median     3Q    Max 
-28.71 -20.48 -10.81  26.42  46.17 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  66.1491     8.1197   8.147 1.35e-09 ***
t             4.5158     0.3726  12.121 4.40e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 24.2 on 35 degrees of freedom
Multiple R-squared:  0.8076,    Adjusted R-squared:  0.8021 
F-statistic: 146.9 on 1 and 35 DF,  p-value: 4.404e-14
>

#滞后一阶
> xlag <- x[2:37]
> x2 <- x[1:36]
#拟合关于延迟变量的自回归模型
> x.fit2 <- lm(x2 ~ xlag)
> summary(x.fit2)
Call:
lm(formula = x2 ~ xlag)
Residuals:
    Min      1Q  Median      3Q     Max 
-15.764  -5.066  -0.703   5.539  20.424 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  7.39226    4.00444   1.846   0.0736 .  
xlag         0.91932    0.02464  37.309   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.936 on 34 degrees of freedom
Multiple R-squared:  0.9762,    Adjusted R-squared:  0.9755 
F-statistic:  1392 on 1 and 34 DF,  p-value: < 2.2e-16
>

> fit1 <- ts(x.fit1$fitted.values, start = 1952)
> fit2 <- ts(x.fit2$fitted.values, start = 1952)
> plot(x,type = "p", pch = 8)
# 关于 时间 t 的线性拟合
> lines(fit1,col =  2)
# 关于滞后变量的拟合
> lines(fit2,col = 4)
>

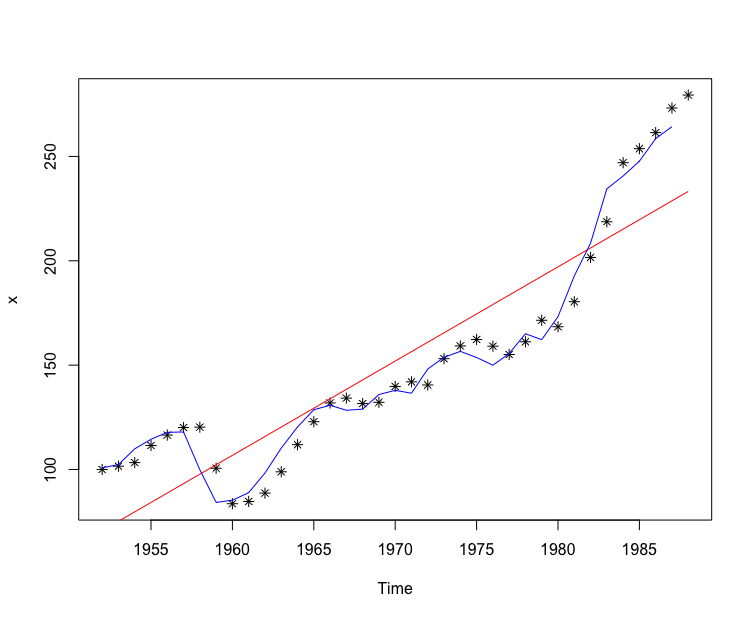
这样，我们就得到了如下两个确定性趋势拟合模型:

$$x_t = 66.1491 + 4.5158 t + \epsilon_t, \epsilon_t \approx N(0,24.2^2) \\ x_t = 7.39226 + 0.9193 x_{t-1} + \epsilon_t , \epsilon_t \approx N(0,7.936^2)$$

---

残差自相关检验

确定性模型拟合好之后，要对该模型的拟合效果进行检验.

如果残差序列显示出纯随机的性质，即

$$E(\epsilon_t \epsilon_{t-j}) = 0, \forall j \geq 1$$ 这说明确定性模型拟合得非常好，已经能够充分提取序列中的相关信息，不需要再对残差序列进行二次信息提取，分析结束.

反之，如果残差序列显示出显著的自相关性，即

$$E(\epsilon_t \epsilon_{t-j}) \neq 0, \exists j \geq 1$$ 这说明确定性模型拟合得不够精确，序列中的相关信息没有得到充分提取，应该对残差序列再次拟合，提取其中残差的相关信息，以提高模型拟合的精度.

自相关性检验我们一般采用 Durbin-Watson 检验，关于 DW检验的解释，我们之前在回归分析的自相关性中讲过了，具体可参看 回归分析篇之自相关性

Durbin $h$ 检验

DW统计量原本适用于回归模型残差自相关性的检验，它要求变量"独立".在自回归场合，即当回归因子包含延迟因变量(计量经济学称之为内生变量)时，有

$$x_t = \beta_0 + \beta_1 \cdot x_{t-1} + \cdots + \beta_k \cdot x_{t-k} + \epsilon_t$$ 残差序列 $\{ \epsilon_t \}$ 的 DW统计量是一个有偏统计量，当 $\rho$ 趋于零时， $DW \neq 2$.在这种场合下使用 DW统计量容易产生残差序列正相关性不显著的误判.

基于这个原因，在 $ARIMA$模型场合，我们都是使用 $Q$统计量和 $LB$统计量检验残差序列的自相关性.

为了克服 $DW$检验的有偏性，Durbin在1970年提出了 DW统计量的两个修正统计量: Durbin t 和 Durbin h 统计量，这两个统计量接近等价.

Durbin h 统计量为:

$$D_h = DW \frac{n}{1 - n \sigma_{\beta}^2} \\ DW = 2 \left( 1 - \frac{\sum_{t-2}^n \epsilon_t \cdot \epsilon_{t-1}}{\sum_{t=1}^n \epsilon_t^2} \right)$$
式中，$n$为观察值序列长度；$\sigma_{\beta}^2$ 为延迟因变量系数的最小二乘估计的方差.

通过对 DW统计量的修正，Durbin t 和 Durbin h 统计量有效地提高了检验的精度，替代DW检验统计量成为延迟因变量场合常用的自相关检验统计量.

---

以上面滞后一阶的残差自回归模型示例做DW检验:

#导入必要的test包
> library(lmtest)
# dw检验
> dwtest(x.fit2, order.by = xlag)
    Durbin-Watson test
data:  x.fit2
DW = 1.8153, p-value = 0.2295
alternative hypothesis: true autocorrelation is greater than 0
>

检验结果显示，残差序列不存在显著相关，我们不需要对第二个趋势拟合模型的残差进行再次拟合.

因为自变量 xlag 和因变量 x具有自相关关系，所以需要使用 Durbin h 检验.

Durbin h检验，就是在调用dwtest()函数时，增加order.by参数去指定延迟因变量

---

残差自相关模型拟合

当残差自相关检验显示残差序列高度自相关时，我们需要对残差序列进行二次拟合，进一步提取残差序列中蕴涵的相关信息.

# 残差序列的自相关图
> acf(x.fit1$residuals)

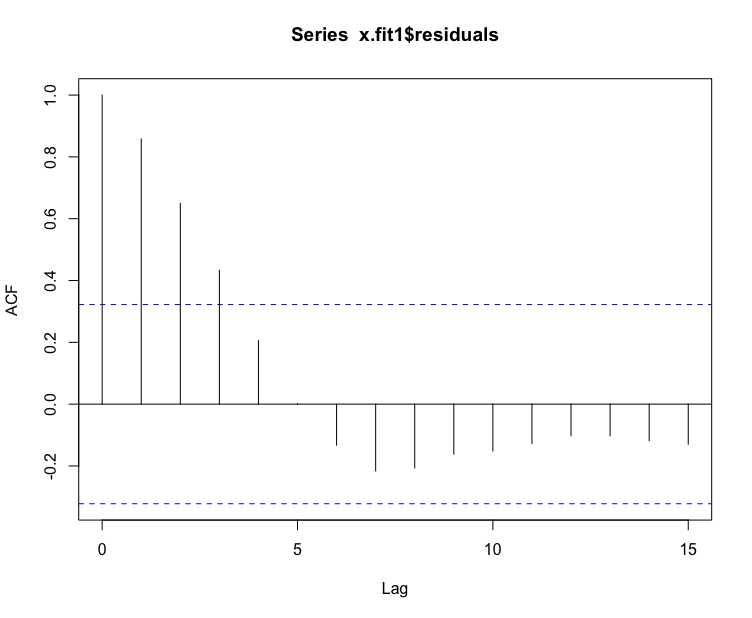
从图中可以看成，滞后2~3阶后的自相关系数在2倍标准差范围内，则可以判断为自相关系数 2阶或者3阶截尾

#残差序列的偏自相关
> pacf(x.fit1$residuals)

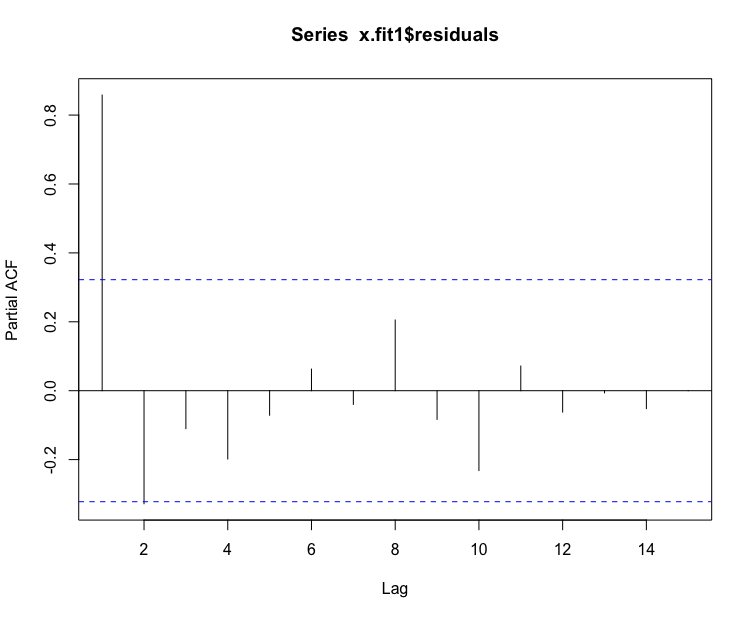
从图中可以看成偏自相关系数 0 阶截尾

#对残差序列进行arima模型拟合
> r.fit <- arima(x.fit1$residuals,order = c(2,0,0), include.mean = F)
> r.fit
Call:
arima(x = x.fit1$residuals, order = c(2, 0, 0), include.mean = F)
Coefficients:
         ar1      ar2
      1.4995  -0.6028
s.e.  0.1274   0.1356
sigma^2 estimated as 50.6:  log likelihood = -126.59,  aic = 259.17
> 
# 残差序列的拟合残差白噪声检验
> for(i in 1:2) print(Box.test(r.fit$residual, lag = 6*i))
    Box-Pierce test
data:  r.fit$residual
X-squared = 3.1979, df = 6, p-value = 0.7836
    Box-Pierce test
data:  r.fit$residual
X-squared = 10.661, df = 12, p-value = 0.5582
>

上面对残差序列拟合 $AR(2)$模型，拟合结果为:

$$\epsilon_t = -1.4995 \epsilon_{t-1} + 0.6028 \epsilon_{t-2} + e_t, e_t \approx N(0,50.6)$$
模型显著性检验显示该拟合模型显著成立.

综合前面的分析，对 1952-1998年中国农业实际国民收入指数序列，我们可以使用如下残差自回归模型进行拟合:

$$\begin{cases} x_t = 66.1491 + 4.5158t + \epsilon_t \\ \epsilon_t = -1.4995 \epsilon_{t-1} + 0.6028 \epsilon_{t-2} + e_t, e_t \approx N(0,50.6) \end{cases}$$