NLP

遗传算法

遗传算法(Genetic Algorithm)遵循『适者生存』、『优胜劣汰』的原则，是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。

遗传算法模拟一个人工种群的进化过程，通过 选择(Selection) 、 交叉(Crossover) 以及 变异(Mutation) 等机制，在每次迭代中都保留一组候选个体，重复此过程，种群经过若干代进化后，理想情况下其适应度达到近似最优的状态。

自从遗传算法被提出以来，其得到了广泛的应用，特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域，遗传算法发挥了很大的作用，提高了一些问题求解的效率。

遗传算法大致过程如下图所示：

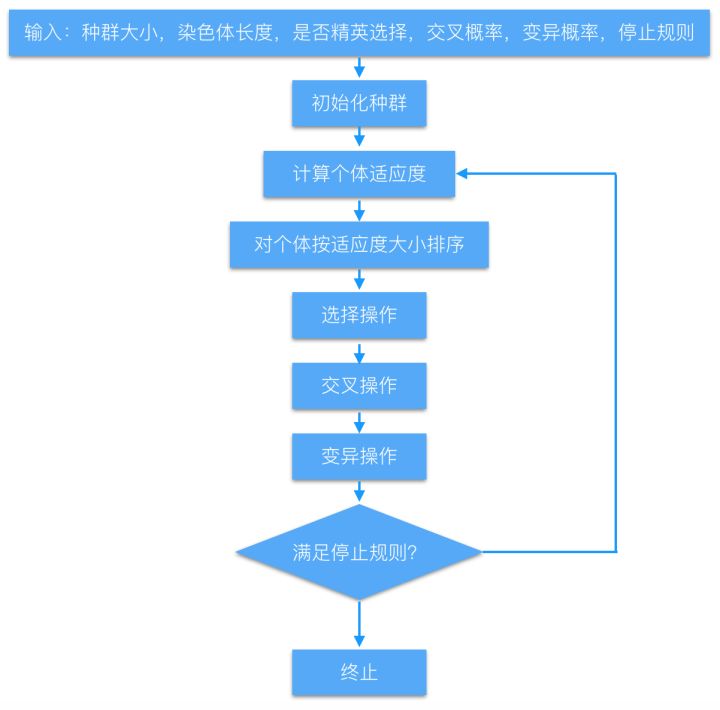
本算法提出的时间比较早，而且得到了广泛的应用，所以资料相比于其他算法会多很多，所以本篇重点在源码分析上。

https://www.zhihu.com/question/23293449 对于算法说明部分，读者可以参考知乎上的前三个回答，都讲的通俗易懂。

参考 中提供的几篇博客讲的都挺好的，读者可以对比的去理解。

---

源码分析

这里分析了两个例子的源码，下载地址为：https://github.com/evilKing/GA

此源码是笔者 fork 其他网友的代码，github出了问题，需要读者自己去创建工程，并按 readme.md 上的目录结构组织文档了

数学函数求极值

首先看 com.ga.math.GA 类，此类解决数学函数求极值的问题，其中用到了遗传算法中的实数编码。

求函数 $f(x,y)$ 的最小值：

$$f(x,y) = 3 - \sin^2(2x) - \sin^2(2y) \\ x \in [0,6] \\ y \in [0,6]$$

将实数进行二进制编码，首先得确定需要多少位二进制能编码出变量的范围。

• 编码
  假如设定求解的精度为小数点后 6 位，可以将 $x,y$ 的解空间划分为 $(6 - 0) \times (1e+6) = 6000000$ 个等分，因为 $2^{22} < 6000000 < 2^{23}$，所以需要 23 位二进制数来表示这些解。换句话说，一个解的编码就是一个 23 位的二进制串，例如 10000100110011001111100 。

• 解码
  对于一条二进制串，如何将它映射到 $[0,9]$ 这个区间上的数值来呢？
  

  $$x = low + decimal(bits) \frac{up - low}{2^{bits\_size} - 1}$$

其中变量定义如下：

• $low$ 表示变量 $x$ 的取值范围下边界
• $up$ 为 $x$ 的上边界
• $bits$ 为二进制串
• $decimal(bits)$ 为取二进制串的十进制数
• $bits\_size$ 为 $bits$ 的长度

通过上述公式就能把二进制串映射到变量的取值范围上。

有一点需要注意，这里是双变量 $x,y$，需要分别将 $x,y$ 编码后直接二进制字符串首尾拼接，计算适应度函数值时再拆分开。

---

先看入口函数：

public static void main(String args[]) {
    GA Tryer = new GA();
    //产生初始种群
    Tryer.ipop = Tryer.initPop();
    //迭代次数
    for (int i = 0; i < 100000; i++) {
        //选择
        Tryer.select();
        //交叉
        Tryer.cross();
        //变异
        Tryer.mutation();
        Tryer.generation = i;
    }
    //计算最优个体的适应度函数值
    double[] x = Tryer.calculatefitnessvalue(Tryer.beststr);
}

上述过程都比较简单，先初始化一个种群，即随机初始化一系列 23 位的二进制串（染色体）；然后迭代的选择、交叉、变异；最后计算最优个体的适应度函数值。

根据具体的目标设置适应度函数，比如这里是要求函数 $f(x,y)$ 的最小值，那该数学函数就成了个体的适应度函数，该函数值小的就应该被淘汰，或者用函数值较大的个体代替。

private String initChr() {
    String res = "";
    for (int i = 0; i < GENE; i++) {
        if (Math.random() > 0.5) {
            res += "0";
        } else {
            res += "1";
        }
    }
    return res;
}

以一定概率随机初始化一条二进制串。其中这里 0 和 1 的设置并不影响最后的结果。

/**
 * 轮盘选择
 * 计算群体上每个个体的适应度值; 
 * 按由个体适应度值所决定的某个规则选择将进入下一代的个体;
 */
private void select() {
    // 所有染色体适应值
    double evals[] = new double[ChrNum];
     // 各染色体选择概率
    double p[] = new double[ChrNum];
    // 累计概率
    double q[] = new double[ChrNum]; 
    double F = 0; // 累计适应值总和
    for (int i = 0; i < ChrNum; i++) {
        // 计算适应度函数值
        evals[i] = calculatefitnessvalue(ipop[i])[2];
        // 记录下种群中的最小值，即最优解
        if (evals[i] < bestfitness){
            bestfitness = evals[i];
            bestgenerations = generation;
            beststr = ipop[i];
        }
        // 所有染色体适应值总和
        F = F + evals[i]; 
    }
    //轮盘赌
    for (int i = 0; i < ChrNum; i++) {
        p[i] = evals[i] / F;
        if (i == 0)
            q[i] = p[i];
        else {
            //计算 p[i] 的累积概率
            q[i] = q[i - 1] + p[i];
        }
    }
    /**
     * 对每个染色体使用轮盘赌选择，所以是两重 for 循环
     */
    for (int i = 0; i < ChrNum; i++) {
        double r = Math.random();
        if (r <= q[0]) {
            ipop[i] = ipop[0];
        } else {
            // 适应度低的以一定概率被适应度高的给取代
            for (int j = 1; j < ChrNum; j++) {
                if (r < q[j]) {
                    ipop[i] = ipop[j];
                }
            }
        }
    }
}

上述过程做了两步：

• 计算每个个体的适应度值
• 利用轮盘赌方法，将适应度较低的个体以一定的概率用适应度高的个体替换
  就是将适应度低的个体淘汰了，同时又保证了种群的个体数量稳定.

其中计算个体适应度的方法如下：

private double[] calculatefitnessvalue(String str) {
    //二进制数前23位为x的二进制字符串，后23位为y的二进制字符串
    int a = Integer.parseInt(str.substring(0, 23), 2);      
    int b = Integer.parseInt(str.substring(23, 46), 2);
    // 将二进制编码转换为实数
    double x =  a * (6.0 - 0) / (Math.pow(2, 23) - 1);    //x的基因
    double y =  b * (6.0 - 0) / (Math.pow(2, 23) - 1);    //y的基因
    //需优化的函数，也即是适应度值
    double fitness = 3 - Math.sin(2 * x) * Math.sin(2 * x) 
                - Math.sin(2 * y) * Math.sin(2 * y);
    double[] returns = { x, y, fitness };
    return returns;
}

计算适应度时，这里需要先将二进制串解码，转成成实数值，然后带入公式计算函数值。

种群的选择操作就完成了，可以看到其中通过计算适应度值，淘汰了适应度较低的个体，剩下的都是相对较高的个体.

其中需要注意，目标是计算函数的最小值，则说明函数值越小，适应度就越高。

/**
 * 交叉操作 交叉率为60%，平均为60%的染色体进行交叉
 */
private void cross() {
    String temp1, temp2;
    //对相邻两染色体进行交叉
    for (int i = 0; i < ChrNum; i++) {
        if (Math.random() < 0.60) {
            //pos位点前后二进制串交叉
            int pos = (int)(Math.random()*GENE)+1;
            //染色体交叉
            temp1 = ipop[i].substring(0, pos) + ipop[(i + 1) % ChrNum].substring(pos); 
            temp2 = ipop[(i + 1) % ChrNum].substring(0, pos) + ipop[i].substring(pos);
            //更新染色体
            ipop[i] = temp1;
            ipop[(i + 1) / ChrNum] = temp2;
        }
    }
}

上述是对相邻的两条染色体，以一定的概率执行交叉，随机生成一个交叉点，然后交换两条染色体的两个部分。

算法没有具体的实现准则，读者可以随机挑选两条染色体进行交叉。

下面再看变异：

/**
 * 基因突变操作 1%基因变异
 */
private void mutation() {
    for (int i = 0; i < 4; i++) {
        //使用随机数可以实现随机选择染色体和染色体的基因位
        int num = (int) (Math.random() * GENE * ChrNum + 1);
        int chromosomeNum = (int) (num / GENE) + 1; // 染色体号
        int mutationNum = num - (chromosomeNum - 1) * GENE; // 基因号
        if (mutationNum == 0) 
            mutationNum = 1;
        chromosomeNum = chromosomeNum - 1;
        if (chromosomeNum >= ChrNum)
            chromosomeNum = 9;
        String temp;
        String a;   //记录变异位点变异后的编码
        if (ipop[chromosomeNum].charAt(mutationNum - 1) == '0') {    //当变异位点为0时
            a = "1";
        } else {   
            a = "0";
        }
        //当变异位点在首、中段和尾时的突变情况
        if (mutationNum == 1) {
            temp = a + ipop[chromosomeNum].substring(mutationNum);
        } else {
            if (mutationNum != GENE) {
                temp = ipop[chromosomeNum].substring(0, mutationNum -1) + a 
                            + ipop[chromosomeNum].substring(mutationNum);
            } else {
                temp = ipop[chromosomeNum].substring(0, mutationNum - 1) + a;
            }
        }
        //记录下变异后的染色体        
        ipop[chromosomeNum] = temp;
    }
}

这步的处理是随机选择四个染色体，每个染色体中随机选择一个基因位进行变异（变异就是将 "0" 变成 "1"，将 "1" 变成 "0"）。

---

经过若干次迭代之后，能得到较优的解；虽然不一定能保证得到的是全局最优解，也有可能得到的依然是局部最优解，这是这类数值解法的问题。

遗传算法能比较快的收敛到最优解，若增大种群中的个体数量，可以更好的找到全局最优解，当然计算效率也降低了。

上面有两个核心的问题，第一是将实数变量编码成 0 1 字符串供遗传算法使用，第二是将目标函数值作为适应度函数.

---

复制图像

下载地址：https://github.com/JgyXyyxy/GA

项目目标是给定一幅图像 A，然后随机创建一幅图像 B，并利用遗传算法将 B 调整成 A，达到复制图像的目的。

程序的主要步骤为：

• 将 3 维的目标图像转换成一维像素数组，每个元素是一个 24 位的 0 1 字符串
• 分别对每个像素应用遗传算法，做选择、交叉、变异等操作
• 其中选择操作的适应度函数为当前像素与目标图像对应位置的像素的汉明距离

像素要应用遗传算法也需要先 编码 ；用 ColorFormat 类中的 boolean[] toBinaryGene(Color color) 方法将 rgb 颜色编码成了 24 位的 0 1 数组，以实现遗传算法所需要的编码要求；同时解码就用 Color binary2Color(boolean[] binary) 方法将 0 1 数组转换为颜色对象。详细过程可以参看源码。

rgb 都是 $[0,255]$ 范围的整数值

---

程序入口为 test.java $\rightarrow$ ChooseImage()，我们直接看菜单 openItem 按钮的点击事件：

// 选择一幅目标图片
String name = chooser.getSelectedFile().getPath();
icon = new ImageIcon(name);
//读取图片属性
picAtri = new PicAtri(name);
......
//启动线程开始复制
startRecover();

下面看 startRecover() 方法：

private void startRecover() throws IOException {
    //最大迭代次数
    count = Integer.parseInt(textfield.getText());
    //目标图像的长宽
    int width = picAtri.getWidth();
    int height = picAtri.getHigh();
    //每个像素设置的种群数量
    int popsize = 16;
    // 整幅图像转换为 0 1 字符串后的长度
    double sum = 0;
    int sumBestFitness = 0;
    //目标图像的颜色数组
    Color[] targetColors = picAtri.getColor();
    sum = 24*targetColors.length;
    //创建一幅空白图像，在这幅图像上生成目标图像
    String image = createBlankImage(width,height);
    PicAtri createdPic = new PicAtri(image);
    //实时显示每步迭代后的效果
    ShowImage createdShow = new ShowImage(createdPic);
    //对每个像素应用遗传算法
    GeneticAlgorithm[] createdPionts = new GeneticAlgorithm[width*height];
    int index = 0;
    //初始化
    for (;index<width*height;index++) {
        //每个像素的适应度函数值是考察与目标像素的差距
        Fitness fitness = new Fitness(targetColors[index]);
        Population population = new Population(popsize,fitness);
        createdPionts[index] = new GeneticAlgorithm(population,createdShow);
    }
    int maxIterNum = count;
    int generation = 1;
    while (generation <= maxIterNum){
        for (int i = picAtri.getMinY();i<height;i++){
            for (int j = picAtri.getMinX();j<width;j++){
                index = j + i*width;
                //每个像素对应的种群进行选择、交叉、变异
                createdPionts[index].evolve(createdPic,j,i);
                sumBestFitness +=createdPionts[index].getBestScore();
            }
        }
        //更新图像，查看迭代效果
        createdPic.writePic();
        createdShow.updatePic();
        //图像复制的精度
        double percent = sumBestFitness/sum;
    }
}

上面的过程都是比较清晰的，主要是对图像的每个像素都应用遗传算法进行选择、交叉、变异。

对单个像素而言，我们看分析下遗传算法的过程，看 GeneticAlgorithm 类的 evolve() 方法：

public void evolve(PicAtri atri, int x, int y) {
    List<Chromosome> childChromosomeList = new ArrayList<Chromosome>();
    //这里设置迭代种群数量次交叉操作
    while (childChromosomeList.size() < population.getPopSize()) {
        // 在交叉前，选择哪两个染色体时，做了选择操作
        //即此时只选择适应度强的染色体进行后续操作，而自然淘汰了适应度差的染色体
        Chromosome p1 = getParentChromosome();
        Chromosome p2 = getParentChromosome();
        //交叉操作比较常规，随机选择一个交叉点进行交换
        List<Chromosome> children = Chromosome.crossover(p1, p2);
        if (children != null) {
            for (Chromosome chro : children) {
                //保证种群数量不变
                if (childChromosomeList.size()<population.getPopSize()) {
                    childChromosomeList.add(chro);
                }else{
                    break;
                }
            }
        }
    }
    population.setPopulation(childChromosomeList);
    //变异操作也比较常规，对每条染色体以一定的概率进行变异，变异位置随机
    mutation();
    //计算迭代一轮后新的适应度函数值
    population.caculteScore();
    //得到适应度最高的染色体更新图像
    Chromosome bestChromosome = population.getBestChromosome();
    bestScore = bestChromosome.getScore();
    Color color = ColorFormat.binary2Color(bestChromosome.getGene());
    atri.setPointAlpha(x,y,color);
}

重点关注种群分数的计算：

public void caculteScore() {
    //计算每条染色体的适应度函数值
    for (Chromosome chromosome:population){
        chromosome.setScore(fitness.calculateFittness(chromosome.getGene()));
    }
    //下面就是统计适应度最高、最低 以及 平均值
    bestFitness = population.get(0).getScore();
    worstFitness = population.get(0).getScore();
    totalFitness= 0;
    for (Chromosome chro : population) {
        if (chro.getScore() >= bestFitness) { //设置最好基因值
            bestFitness = chro.getScore();
            bestChromosome = chro;
        }
        if (chro.getScore() < worstFitness) { //设置最坏基因值
            worstFitness = chro.getScore();
        }
        totalFitness += chro.getScore();
    }
    averageFitness = totalFitness / popSize;
    //因为精度问题导致的平均值大于最好值，将平均值设置成最好值
    averageFitness = averageFitness > bestFitness ? bestFitness : averageFitness;
}

我们其实只需要适应度最高的染色体，用来更新图像。

下面重点看下适应度函数的计算，查看 Fitness.calculateFittness() 方法：

public double calculateFittness(boolean[] srcGene) {
    double fit = 0;
    //获得目标染色体
    boolean[] targetGene = ColorFormat.toBinaryGene(target);
    //对比当前染色体与目标染色体相同的基因有多少，以此作为适应度值
    for (int i = 0;i<24;i++){
        if (srcGene[i] == targetGene[i])
            fit=fit+1;
    }
    return fit;
}

其中适应度值越高，则说明当前像素与目标像素越接近，图像复制越成功，这就是我们最终实现的目标。

---

再回头看上面的过程，其实需要注意的就两处，第一是如何编码来表示像素，使之能应用遗传算法，第二是如何设置适应度函数，这与我们要实现的目标有关。

至于一遗传算法的选择、交叉、变异等操作，实现起来其实大同小异。

---

小结

遗传算法的理论部分网上已经有非常多的资料了，读者可以先阅读笔者推荐的几篇博客；

上面的两个例子是为了说明实数型如何编码；怎么应用遗传算法，适应度函数如何设置；这也是我们应用遗传算法做具体需求时需要考虑的核心问题。

在其他应用领域，大多是用遗传算法来做模型的参数估计，可以对参数进行编码，将模型对测试语料库的评估值作为适应度，淘汰掉使测试结果效果不太好的参数，这样可以快速的得到最优的参数估计值。

---

参考

• http://songshuhui.net/archives/10462
• https://www.zhihu.com/question/23293449
• https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650728869&idx=4&sn=377e2da3d6fe3ec06154d4cc01a9c6e0&scene=0#wechat_redirect
• http://blog.csdn.net/u010451580/article/details/51178225