回归分析篇

自相关性

无论是在介绍一元还是多元线性回归模型时，我们总假定其随机误差项是不相关的，即

$$cov(\epsilon_i,\epsilon_j) = 0, \ \ \ \ i \neq j$$
表示不同时点的误差项之间不相关。

如果一个回归模型不满足上式，即$cov(\epsilon_i,\epsilon_j) \neq 0$，则我们称随机误差项之间存在着自相关现象。

这里的自相关现象不是指两个或两个以上的变量之间的相关关系，而指的是一个变量前后期数值之间存在的相关关系。比如时间序列中，$t$ 时刻的值与 $t-1$ 时刻的值有关

---

自相关性产生的原因

1. 遗漏关键变量时会产生序列的自相关性
   如果忽略了一个或几个重要的变量，而这些遗漏的关键变量在时间顺序上的影响是正相关的，回归模型中的误差项就会具有明显的正相关，这是因为误差包含了遗漏变量的影响

2. 经济变量的滞后性会给序列带来自相关性
   许多经济变量都会产生滞后影响，例如物价指数、基建投资、国民收入、消费、货币发行量等都有一定的滞后性。在这样的时间序列数据中，顺序观测值之间的相关现象是很自然的。经济现象中的自相关一般是正的

3. 采用错误的回归函数形式也可能引起自相关性
   假设某实际问题的正确回归函数应由指数形式

   $$y = \beta_0 exp(\beta_1 x + \epsilon)$$ 来表示，但是，研究者误用线性回归模型 $$y = \beta_0 + \beta_1 x + \epsilon'$$ 表示，这时误差项$\epsilon'$也表现为自相关性

4. 蛛网现象也可能带来序列的自相关性
   蛛网现象比较复杂，我们不会去介绍，读者可以自行百度学习

5. 因对数据加工整理而导致误差项之间产生自相关性
   在回归分析建模中，我们经常要对原始数据进行一些处理，如在具有季节性时序资料的建模中，我们常常要消除季节性，对数据作修匀处理。但是如果采用了不恰当的差分变换，这样也会带来序列的自相关性

---

自相关带来的问题

当一个线性回归模型的随机误差项存在序列相关时，就违背了线性回归方程的基本假设，如果任然直接用普通最小二乘法估计未知参数，将会产生严重后果

1. 参数的估计值不再具有最小方差线性无偏性

2. 均方误差 $MSE$ 可能严重低估误差项的方差

3. 容易导致对 $t$ 值评价过高，常用的 $F$ 检验和 $t$ 检验失效。如果忽视这一点，可能导致得出回归参数统计检验为显著，但实际上并不显著的严重错误结论

4. 当存在序列相关时，$\hat{\beta}$任然是 $\beta$的无偏估计量，但在任一特定的样本中，$\hat{\beta}$ 可能严重歪曲 $\beta$ 的真实情况，即最小二乘估计量对抽样波动变得非常敏感

5. 如果不加处理地运用普通最小二乘法估计模型参数，用此模型进行预测和进行结构分析将会带来较大的方差，甚至错误的解释

---

自相关性的检验

图示检验法

图示法比较直观，它是把给定的回归模型直接用普通最小二乘法估计参数，求出残差项 $e_t$，$e_t$作为随机项 $\epsilon_t$ 的真实值的估计值，再描绘出 $e_t$的散点图，根据 $e_t$的相关性来判断随机项 $\epsilon_t$的序列相关性

残差 $e_t$ 的散点图通常有两种绘制方式:

1. 绘制 $e_t, e_{t-1}$ 的散点图
   用 $(e_t, e_{t-1}),t=2,3,\cdots,n$ 作为散点绘图。如果大部分点落在第 $I,III$象限，表明随机扰动项 $epsilon_t$ 存在着正的序列相关，如下图(a)；如果大部分点落在第 $II,IV$象限，那么随机扰动项 $\epsilon_t$ 存在着负相关，如下图(b)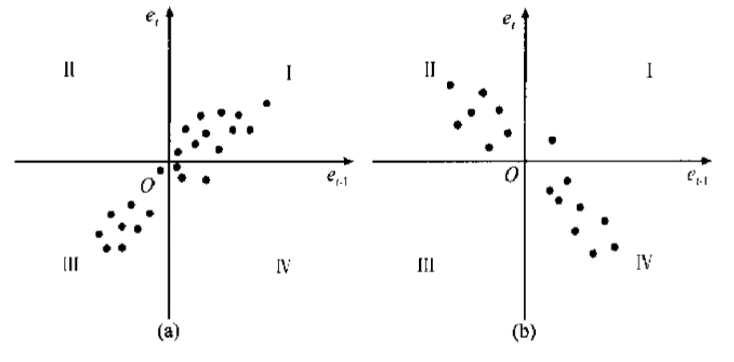

   

2. 按照时间顺序绘制回归残差项 $e_t$ 的图形
   如果 $e_t, t = 1,2,\cdots,n$ 随着 $t$ 的变化逐次有规律地变化，呈现锯齿形或循环形状的变化，就可断言 $e_t$ 存在相关，表明 $\epsilon_t$ 存在着序列相关
   如果 $e_t$ 随着 $t$ 的变化逐次变化并不断地改变符号，如下图(a)，那么随机扰动项 $\epsilon_t$存在负的序列相关，这种现象称为蛛网现象
   如果 $e_t$ 随着 $t$ 的变化逐次变化并不频繁地改变符号，而是几个正的 $e_t$ 后面跟着几个负的，则表明随机扰动项 $\epsilon_t$ 存在正的序列相关，如下图(b)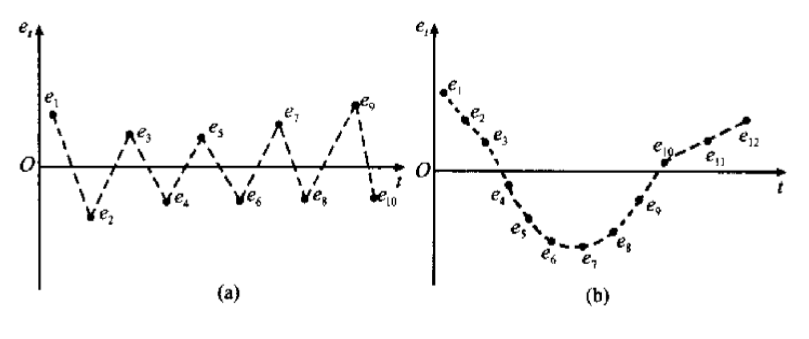

   

---

自相关系数法

误差序列 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 的自相关系数定义为

$$\rho = \frac{\sum_{t = 2}^n{\epsilon_t \epsilon_{t-1}}}{\sqrt{\sum_{t=2}^n{\epsilon_t^2}}\sqrt{\sum_{t=2}^n{\epsilon_{t-1}^2}}}$$
自相关系数 $\rho$ 的取值范围是 $[-1,1]$，当 $\rho$ 接近1时，表明误差序列存在正相关，当 $\rho$ 接近 -1 时，表明误差序列存在负相关

在实际应用中，由于$\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 的真实值是未知的，需要用估计值 $e_t$来代替，于是有

$$\hat{\rho} = \frac{\sum_{t = 2}^n{e_t e_{t-1}}}{\sqrt{\sum_{t=2}^n{e_t^2}}\sqrt{\sum_{t=2}^n{e_{t-1}^2}}}$$
$\hat{\rho}$作为自相关系数 $\rho$ 的估计值与样本量有关，需要做统计显著性检验才能确定自相关性的存在

---

通常采用下面介绍的DW检验代替对 $\hat{\rho}$的检验:

DW检验是一种适用于小样本的检验方法。

DW检验只能用于检验随机扰动项具有一阶自回归形式的序列相关问题。

随机扰动项的一阶自回归形式为

$$\epsilon_t = \rho \epsilon_{t-1} + u_t$$ 为了检验序列的相关性，构造假设 $$H_0 : \rho = 0$$ 为了检验上述假设，构造DW统计量首先要求出回归估计式的残差 $e_t$，定义DW统计量为 $$DW = \frac{\sum_{t=2}^n{(e_t - e_{t-1})^2}}{\sum_{t=2}^n{e_t^2}}$$ 其中，$e_t = y_t - \hat{y_t}, t = 1,2,\cdots,n$

下面推导DW值的取值范围:

$$DW = \frac{\sum_{t=2}^n{e_t^2} + \sum_{t=2}^n{e_{t-1}^2} - 2 \sum_{t=2}^n{e_t e_{t-1}}}{\sum_{t=2}^n{e_t^2}}$$ 如果认为 $\sum_{t=2}^n{e_t^2}$ 与 $\sum_{t=2}^n{e_{t-1}^2}$ 近似相等，则 $$DW \approx 2 \left[ 1 - \frac{\sum_{t=2}^n{e_t e_{t-1}}}{\sum_{t=2}^n{e_t^2}} \right]$$ 同样，在认为 $\sum_{t=2}^n{e_t^2}$ 与 $\sum_{t=2}^n{e_{t-1}^2}$ 近视相等时，则 $$\hat{\rho} \approx \frac{\sum_{t=2}^n{e_t e_{t-1}}}{\sum_{t=2}^n{e_t^2}}$$ 因此， $$DW \approx 2 (1 - \hat{\rho})$$ 因而DW值与 $\hat{\rho}$的对应关系为下表:

$\rho$	$DW$	误差项的自相关性
-1	4	完全负自相关
(-1,0)	(2,4)	负自相关
0	2	无自相关
(0,1)	(0,2)	正自相关
1	0	完全正自相关

所有由上述讨论可知 $DW$ 的取值范围为

$$0 \leq DW \leq 4$$

根据样本容量 $n$ 和解释变量的数目 $k$（这里包括常数项）查 $DW$ 分布表，得临界值 $d_L$ 和 $d_U$，然后依下图考察计算得到的DW值，以决定模型的自相关状态:

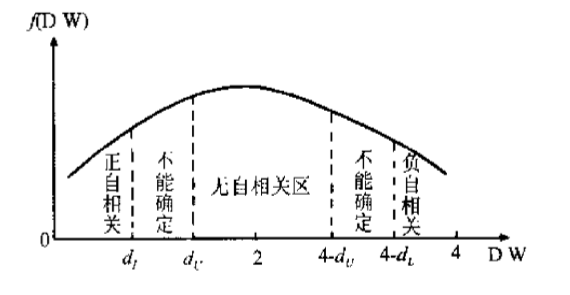
需要注意的是，DW检验尽管有着广泛的应用，但也有明显的缺点和局限性:

1. DW 检验有两个不能确定的区域，一旦 DW 值落在这两个区域，就无法判断。这时，只有增大样本容量或选取其他方法

2. DW 统计量的上、下界表要求 $n > 15$ ，这是因为样本如果再小，利用残差就很难对自相关的存在性作出比较正确的诊断

3. DW 检验不适用随机项具有高阶序列相关的检验

---

处理自相关性

当一个回归模型存在序列相关性时，首先要查明序列相关产生的原因。

如果是回归模型选用不当，则应该用适当的回归模型；如果是缺少重要的自变量，则应增加自变量；如果以上两种方法都不能消除序列相关性，则需采用差分法、自回归法、移动平均法，或者这些方法的综合运用等方法处理。

下面介绍迭代法和差分法，至于自回归法和移动平均法等在时间序列篇中再细讲。

迭代法

以一元线性回归模型为例，设一元线性回归模型的误差项存在一阶自相关

$$y_t = \beta_0 + \beta_1 x_t + \epsilon_t \\ \epsilon_t = \rho \epsilon_{t-1} + u_t$$ $u_t$满足随机扰动项的基本假设，则 $$\begin{cases} E(u_t) = 0 \\ cov(u_t,u_s) = \begin{cases} \sigma^2,t=s \\ 0,t \neq s \end{cases} \end{cases}$$ 其中，$t,s = 1,2,\cdots,n$
根据上述回归模型有 $$y_{t-1} = \beta_0 + \beta_1 x_{t-1} + \epsilon_{t-1}$$ 两边分别乘以 $\rho$，在与原回归模型相减，则有 $$(y_t - \rho y_{t-1}) = (\beta_0 - \rho \beta_0) + \beta_1 (x_t - \rho x_{t-1}) + (\epsilon_t - \rho \epsilon_{t-1})$$ 令: $$y_t' = y_t - \rho y_{t-1} \\ x_t' = x_t - \rho x_{t-1} \\ \beta_0' = \beta_0 (1 - \rho), \beta_1' = \beta_1$$ 于是模型变成了 $$y_t' = \beta_0' + \beta_1' x_t' + u_t$$ 具有独立随机误差项，它已满足线性回归模型的基本假设，用普通最小二乘法估计的参数估计量具有通常的优良性

由于变量替换的自相关系数 $\rho$ 是未知的，需要用 $\hat{\rho} \approx 1 - \frac{1}{2} DW$ 对 $\rho$ 做估计，然后带入到最后的模型中作普通最小二乘回归，即可求解

在实际问题中，往往误差项并不是简单的一阶自相关，而是更负责的自相关形式，则误差项 $u_t$ 有可能任然存在自相关，则需要进一步重复上述步骤，先对误差 $u_t$ 做 $DW$ 检验，然后再用迭代法，直至最后误差项消除自相关性为止

---

差分法

差分法就是用增量数据代替原来的样本数据，将原来的回归模型变为差分形式的模型。一阶差分法通常适用于原模型存在较高程度的一阶自相关的情形

在迭代法中，当 $\rho = 1$ 时，得

$$(y_t - y_{t-1}) = \beta_1 (x_t - x_{t-1}) + (\epsilon_t - \epsilon_{t-1})$$ 以 $\Delta y_t = y_t - y_{t-1}, \Delta x_t = x_t - x_{t-1}$带入上式，则 $$\Delta y_t = \beta_1 \Delta x_t + u_t$$ 不存在序列的自相关，它是以差分数据 $\Delta y_t$ 和 $\Delta x_t$ 为样本的回归方程。

这样不带常数项的回归方程用最小二乘法估计，得

$$\hat{\beta}_1 = \frac{\sum_{t=2}^n{\Delta y_t \Delta x_t}}{\sum_{t=2}^n{\Delta x_t^2}}$$ 一阶差分法的应用条件是自相关系数 $\rho = 1$

在实际应用中，$\rho$ 接近 1 时我们采用差分法而不是迭代法

---

R程序演示