@evilking 2018-04-30T16:40:28.000000Z 字数 17581 阅读 3347

NLP

LDA 主题模型

LDA 是两个常用模型的简称：线性判别分析（Linear Discriminant Analysis）和潜在狄利克雷分布主题模型（Latent Dirichlet Allocation），在之前的篇章中我们已经详细讲解了线性判别分析模型，本篇就详细讲解主题模型。

该模型主要是用来给文档划分主题，可得出每篇文档的主题分布，以及每个主题下的词分布。但要理解该模型需要有一些数学功底，比如 Gamma分布、Beta分布、多项式分布、Dirichlet分布等等。

理论部分网友总结的已经很详细了，特别是 《LDA数学八卦》 、 《LDA漫游指南》 这两篇，强烈推荐读一读，本篇理论部分大多都是摘录至这两篇文档，大致总结一些比较重点的部分供初学者快速学习。

数学基础

LDA主题模型主要是用到了 Dirichelt-Multinomial共轭结构，要理解多项式分布，就先要理解伯努利分布、二项分布，而Dirichelt分布又是Beta分布在多维上的扩展，Beta分布又是二项分布的共轭先验分布。这几个分布都与 Gamma函数有关，所以我们下面一个个介绍这些统计中常用的分布函数。

Gamma函数

所谓的 gamma函数其实就是阶乘的函数形式，比如 $3! = 6$ ，但要问你 $\frac{1}{2}! = ?$ ，如果没有 gamma 函数就无法回答了，欧拉经过不懈的努力，最终给出了更一般的函数形式 gamma 函数：

$\Gamma(x) = \int_0^{+\infty} e^{-t} t^{x-1} d_t \quad (x>0)$
可以直接算出

$\Gamma(1) = 1$ ，也可以算出

$\Gamma(\frac{1}{2}) = \sqrt{\pi}$ .

详细计算过程参考《LDA漫游指南》2.1 gamma函数一节.

Gamma函数有个重要的性质： $\Gamma(x+1) = x \Gamma(x)$

也因为该性质可得： $\Gamma(n) = (n-1)!$

该性质可用分部积分法展开求解，不难证明，详细可参看《LDA漫游指南》2.1 gamma函数一节.

二项分布(Binomial distribution)

概率论中，二项分布即为重复 $n$ 次独立的伯努利试验。比如投掷硬币，正面朝上的概率为 $p$ ，反面朝上的概率即为 $1-p$ ，投掷一次，即为一次伯努利试验，投掷 $n$ 次，即为 $n$ 次伯努利试验，又叫做概率为 $p$ 的二项分布。

现假设你投掷了 $n$ 次硬币，有 $k$ 次正面朝上，但你不确定具体在哪 $k$ 次，所以是先从 $n$ 次中任取 $k$ 次，即 $C_n^k = \left(\begin{matrix} n \\ k \end{matrix} \right)$ ，那么投掷 $k$ 次正面朝上的概率为：

$f(k;n,p) = Pr(X = k) = \left(\begin{matrix} n \\ k \end{matrix} \right) p^k (1-p)^{n-k}$
其中，

$\left(\begin{matrix} n \\ k \end{matrix} \right) = \frac{n!}{k!(n-k)!}$

beta分布(beta distribution)

在概率论中，beta分布是指一组定义在区间 $(0,1)$ 的连续概率分布，有两个参数 $\alpha$ 和 $\beta$ ，且 $\alpha,\beta > 0$ .

Beta分布的概率密度函数是：

$\begin{array} & f(x;\alpha,\beta) &=& \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1 u^{\alpha-1}(1-u)^{\beta-1}} d_u \\ &=& \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} \\ &=& \frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1} \end{array}$

随机变量 $X$ 服从参数为 $\alpha,\beta$ 的beta分布通常写为： $X \approx Beta(\alpha,\beta)$

这个式子中分母的函数称为 B 函数，在LDA算法 Gibbs Sampling 采样公式中也有用到.

$B(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} = \int_0^1 u^{a-1}(1-u)^{b-1} d_u$
该式的证明参考《LDA漫游指南》2.3 beta分布一节，其中证明2 看的更好理解一些。

多项分布(multinomial distribution)

多项分布式二项分布的推广扩展，在 $n$ 词独立试验中每次只输出 $k$ 中结果中的一个，且每种结果都有一个确定的概率 $p_k$ 。多项分布给出了在多种输出状态的情况下，关于成功次数的各种组合的概率。

举个例子，投掷 $n$ 次骰子，骰子共有 6 种结果输出，且 1 点出现概率为 $p_1$ ，2 点出现概率 $p_2$ ， $\cdots$ ，多项分布给出了在 $n$ 次试验中，骰子 1 点出现 $x_1$ 次，2 点出现 $x_2$ 次，3 点出现 $x_3$ 次， $\cdots$ ，6 点出现 $x_6$ 次。这个结果组合的概率为：

$\begin{array} & f(x_1,\cdots,x_k;n,p_1,\cdots,p_k) &=& Pr(X_1 = x_1 \ and \ \cdots \ and \ X_k = x_k) \\&=& \begin{cases} \frac{n!}{x_1! \cdots x_k!} p_1^{x_1} \cdots p_k^{x_k} & when \ \sum_{i=1}^k x_i = n \\ 0 & otherwise \end{cases} \end{array}$

也可以用 gamma 函数表示：

$f(x_1,\cdots,x_k;n,p_1,\cdots,p_k) = \frac{\Gamma(\sum_i (x_i +1))}{\prod_i \Gamma(x_i + 1)} \prod_{i=1}^k p_i^{x_i}$

狄利克雷分布(dirichlet distribution)

dirichlet 分布是beta分布在多项情况下的推广，也是多项分布的共轭先验分布。

dirichlet 分布的概率密度函数如下：

$f(p_1,\cdots,p_{k-1};\alpha_1,\cdots,\alpha_k) = \frac{1}{\Delta(\vec{\alpha})} \prod_{i=1}^k p_i^{\alpha_i - 1}$

其中，

$\Delta(\vec{\alpha}) = \frac{\prod_{i=1}^k \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^k \alpha_i)}$

二项分布和多项分布很相似，Beta分布和Dirichlet分布很相似。

另一个重要的公式是：

$\int \prod_{i=1}^k p_i^{\alpha_i - 1} d_{\vec{p}} = \Delta(\vec{\alpha}) = \frac{\prod_{i=1}^k \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^k \alpha_i)}$

共轭先验分布(conjugacy prior)

在贝叶斯概率理论中，如果后验分布和先验分布的概率分布函数相同，则先验分布和后验分布被叫做共轭分布，先验分布被叫做似然函数的共轭先验分布。

而什么叫似然函数呢？举个例子，Beta分布式二项分布的共轭先验，先验分布与后验分布当二项分布的 $n \rightarrow \infty$ 时才成立，但实际应用中这显然是不可能的，所以我们取 $n$ 为一个有限的常数去近似，所以此时的“二项分布函数”就是“似然函数”。

具体来说，Beta分布是二项分布的共轭先验分布：

$Beta(p|\alpha,\beta) + BinomCount(m_1,m_2) = Beta(p|\alpha+m_1,\beta+m2)$
这就是 Beta-Binomial 共轭.

而Dirichlet分布是多项式分布的共轭先验分布：

$Dir(\vec{p} | \vec{\alpha}) + MultCount(\vec{m}) = Dir(\vec{p} | \vec{\alpha} + \vec{m})$
这就是 Dirichlet-Multinomial 共轭.

关于共轭先验分布的证明和解释，在《LDA数学八卦》中讲的很详细，其中举得掷骰子的例子也很经典，强烈推荐读者去看看

Beta/Dirchlet 分布的一个性质

上面都是直接给出的几个分布函数的概率密度函数，因为本篇主要不是介绍理论，具体的理论细节都在《LDA数学八卦》《LDA漫游指南》中讲了。但在 LDA 模型中，用到的一个非常重要的计算是求 Beta/Dirichlet 分布的期望.

如果 $p \approx Beta(t|\alpha,\beta)$ ，则

$\begin{array} & E(p) &=& \int_0^1 t*Beta(t|\alpha,\beta) d_t \\&=& \int_0^1 t*\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} t^{\alpha-1} (1-t)^{\beta - 1} d_t \\&=& \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \int_0^1 t^{\alpha} (1-t)^{\beta-1} d_t \end{array}$

上式右边的积分对应到概率分布 $Beta(t|\alpha+1,\beta)$ ，对于这个分布，我们有

$\int_0^1 \frac{\Gamma(\alpha+\beta+1)}{\Gamma(\alpha+1)\Gamma(\beta)} t^{\alpha} (1-t)^{\beta-1} d_t = 1$

把上式带入 $E(p)$ 中，得：

$\begin{array} & E(p) &=& \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \frac{\Gamma(\alpha + 1)\Gamma(\beta)}{\Gamma(\alpha+\beta + 1)} \\&=& \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + 1)} \cdot \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)} \\&=& \frac{\alpha}{\alpha + \beta} \end{array}$

因为 $\Gamma(n) = (n-1)!$

这说明，对于 Beta 分布的随机变量，其均值可用 $\frac{\alpha}{\alpha + \beta}$ 来估计。

Dirichlet 分布也有类似的结论，如果 $\vec{p} \approx Dir(\vec{t}|\vec{\alpha})$ ，同样可以证明：

$E(\vec{p}) = \left( \frac{\alpha_1}{\sum_{i=1}^K \alpha_i},\frac{\alpha_2}{\sum_{i=1}^K \alpha_i},\cdots,\frac{\alpha_K}{\sum_{i=1}^K \alpha_i} \right)$

MCMC和Gibbs Sampling

LDA 模型求解主要有两种方法：变分推断EM算法和 Gibbs 采样算法；由于 Gibbs采样算法效率更高，所以一般LDA的实现都是采样的 Gibbs 采样.

关于蒙特卡罗算法和 Gibbs 采样算法，在 http://www.cnblogs.com/pinard/p/6645766.html 这个系列的博文中讲的非常清楚了，读者可以直接看这篇博文进行学习。

不过这篇博文更多的是用通俗的语言去理解 Gibbs采样，应用于 LDA 模型，理论部分可以参考《LDA漫游指南》中 3.3 节讲推导过程。

LDA

到这里关于 LDA 模型涉及到的数学知识就OK了，下面介绍主题模型.

LDA 是从PLSA模型加入贝叶斯框架演变而来，在PLSA模型中假设文档是这样生成的：文档是由多个主题混合而成，而每个主题由对应的词组成。

上帝有两种类型的骰子，一类是 doc-topic 骰子，每个 doc-topic 骰子有 K 个面，每个面是一个 topic 的编号；一类是 topic-word 骰子，每个 topic-word 骰子有 V 个面，每个面对应一个词；
上帝一共有 K 个 topic-word 骰子，每个骰子有一个编号，编号从 1 到 K；
生成每篇文档之前，上帝都先为这篇文章制造一个特定的 doc-topic 骰子，然后重复如下过程生成文档中的词:
- 骰子这个 doc-topic 骰子，得到一个 topic 编号 z
- 选择 K 个 topic-word 骰子中编号为 z 的那个，骰子这个骰子，于是得到一个词.

plsa

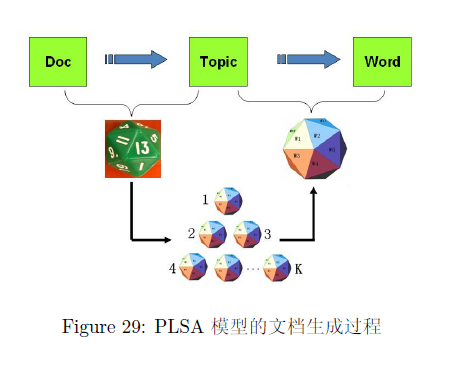
游戏中的 K 个 topic-word 骰子，我们可以记为 $\vec{\varphi}_1,\cdots,\vec{\varphi}_K$ ，对于包含 M 篇文档的语料 $C = (d_1,d_2,\cdots,d_M)$ 中的每篇文档 $d_m$ ，都会有一个特定的 doc-topic 骰子 $\vec{\theta}_m$ ，所有对应的骰子记为 $\vec{\theta}_1,\cdots,\vec{\theta}_M$ 。为了方便，我们假设每个词 $w$ 都是一个编号，对应到 topic-word 骰子的面。

于是在PLSA模型中，第 $m$ 篇文档 $d_m$ 中的每个词的生成概率为

$p(w|d_m) = \sum_{z=1}^K p(w|z)p(z|d_m) = \sum_{z=1}^K \varphi_{zw}\theta_{mz}$

所以整篇文档的生成概率为

$p(\vec{w}|d_m) = \prod_{i=1}^n \sum_{z=1}^K p(w_i | z)p(z|d_m) = \prod_{i=1}^n \sum_{z=1}^K \varphi_{zw_t}\theta_{dz}$

贝叶斯学派却不这么认为，在这个模型中 doc-topic 骰子 $\vec{\theta}_m$ 和 topic-word 骰子 $\vec{\varphi}_k$ 对应的概率分布都是模型中的参数，参数都是随机变量，怎么能没有先验分布呢？于是需要对 PLSA 模型加上贝叶斯框架加以改造。

由于 $\vec{\theta}_m$ 和 $\vec{\varphi}_k$ 都对应到多项式分布，所以先验分布的一个好的选择就是 Dirichlet分布，于是我们就得到了 LDA(Latent Dirichlet Allocation) 模型。

lda

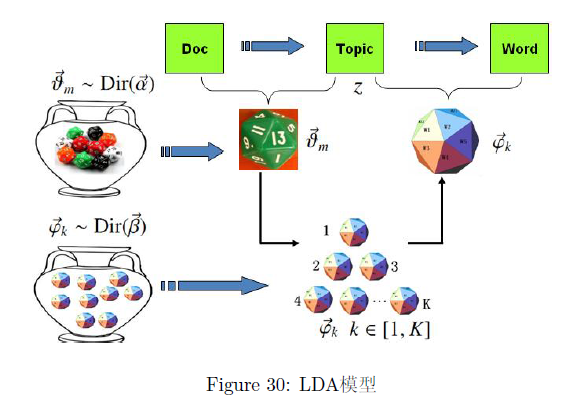
上帝有两大坛子的骰子，第一个坛子装的是 doc-topic 骰子，第二个坛子装的是 topic-word 骰子；
上帝随机的从第二个坛子中独立的抽取了 K 个 topic-word 骰子，编号为 1 到 K；
每次生成一篇新的文档前，上帝先从第一个坛子中随机抽取一个 doc-topic 骰子，然后重复如下过程生成文档中的词：
- 骰子这个 doc-topic 骰子，得到一个 topic 编号 z
- 选择 K 个topic-word 骰子中编号为 z 的那个，投掷这个骰子，于是得到一个词

上式过程涉及到两个物理过程：

$\vec{\alpha} \rightarrow \vec{\theta}_m \rightarrow \vec{z}_m$ 表示生成第 $m$ 篇文档中的所有词对应的 topics。显然 $\vec{\alpha} \rightarrow \vec{\theta}_m$ 对应于 Dirichlet分布， $\vec{\theta}_m \rightarrow \vec{z}_m$ 对应于 Multinomial 分布，所以整体是一个 Dirichlet-Multinomial 共轭结构；
$\vec{\beta} \rightarrow \vec{\varphi}_k \rightarrow w_{m,n}|k = z_{m,n}$ ，在 $k = z_{m,n}$ 的限制下，第 $k$ 个主题-词分布生成第 $m$ 篇文档的第 $n$ 个单词。此时 $\vec{\beta} \rightarrow \vec{\varphi}_k$ 对应于 Dirichlet 分布， $\vec{\varphi}_k \rightarrow w_{m,n}$ 对应与 Multinomial 分布，所以整体也还是一个 Dirichlet-Multinomial 共轭结构；

对于第一个物理过程，我们有

$\begin{array} & p(\vec{z}_m | \vec{\alpha}) &=& \int p(\vec{z}_m | \vec{\theta}) p(\vec{\theta} | \vec{\alpha}) d_{\vec{\theta}} \\&=& \int \prod_{k=1}^K \theta_k^{n_m^{k}} Dir(\vec{\theta} | \vec{\alpha}) d_{\vec{\theta}} \\&=& \int \prod_{k=1}^K \theta_k^{n_m^{k}} \frac{1}{\Delta(\vec{\alpha})} \prod_{k=1}^K \theta_k^{\alpha_k - 1} d_{\vec{\theta}} \\&=& \frac{1}{\Delta(\vec{\alpha})} \int \prod_{k=1}^K \theta_k^{n_m^{k} + \alpha_k - 1} d_{\vec{\theta}} \\&=& \frac{\Delta(\vec{n}_m + \vec{\alpha})}{\Delta(\vec{\alpha})} \end{array}$

其中 $\vec{n}_m = (n_m^{(1)},\cdots,n_m^{(K)})$ ， $n_m^{(k)}$ 表示第 m 篇文档中第 k 个 topic 产生的词的个数。进一步，利用 Dirichlet-Multiomial 共轭结构，我们得到参数 $\vec{\theta}_m$ 的后验分布恰好是

$Dir(\vec{\theta}_m | \vec{n}_m + \vec{\alpha})$

由于语料中 $M$ 篇文档的 topics 生成过程相互独立，所以我们得到 $M$ 个相互独立的 Dirichlet-Multinomial 共轭结构，从而我们可以得到整个语料中 topics 生成概率

$\begin{array} & p(\vec{z} | \vec{\alpha}) &=& \prod_{m=1}^M p(\vec{z}_m | \vec{\alpha}) \\&=& \prod_{m=1}^M \frac{\Delta(\vec{n}_m + \vec{\alpha})}{\Delta(\vec{\alpha})} \end{array}$

类似于第一个物理过程，第二个物理过程我们可以得到：

$p(\vec{w}_{(k)} | \vec{\beta}) = \frac{\Delta(\vec{n}_k + \vec{\beta})}{\Delta(\vec{\beta})}$

其中 $\vec{n}_k = (n_k^{(1)},\cdots,n_k^{(V)})$ ， $n_k^{(t)}$ 表示第 $k$ 个 topic 产生的词中 word t 的个数。进一步，利用 Dirichlet-Multiomial 共轭结构，我们得到参数 $\vec{\varphi}_k$ 的后验分布恰好是

$Dir(\vec{\varphi}_k | \vec{n}_k + \vec{\beta})$

而语料中 $K$ 个 topics 生成words 的过程相互独立，所以我们得到 $K$ 个相互独立的 Dirichlet-Multinomial 共轭结构，从而我们可以得到整个语料中词生成概率：

$\begin{array} & p(\vec{w} | \vec{z},\vec{\beta}) &=& p(\vec{w}' | \vec{z}',\vec{\beta}) \\&=& \prod_{k=1}^K p(\vec{w}_{(k)} | \vec{z}_{(k)},\vec{\beta}) \\&=& \prod_{k=1}^K \frac{\Delta(\vec{n}_k + \vec{\beta})}{\Delta(\vec{\beta})} \end{array}$

于是对于整个语料库的生成概率，我们可以得到：

$\begin{array} & p(\vec{w},\vec{z} | \vec{\alpha},\vec{\beta}) &=& p(\vec{w} | \vec{z},\vec{\beta}) p(\vec{z} | \vec{\alpha}) \\&=& \prod_{k=1}^K \frac{\Delta(\vec{n}_k + \vec{\beta})}{\Delta(\vec{\beta})} \prod_{m=1}^M \frac{\Delta(\vec{n}_m + \vec{\alpha})}{\Delta(\vec{\alpha})} \end{array}$

此处符号表示稍微不够严谨，向量 $\vec{n}_k,\vec{n}_m$ 都是用 $n$ 表示，主要是通过下标进行区分， $k$ 下标为 topic 编号， $m$ 下标为文档编号。

这一小节摘录至《LDA数学八卦》，这里面把LDA的两个过程讲的比较清楚

Gibbs采样应用过程

有了联合分布 $p(\vec{w},\vec{z})$ ，万能的 MCMC 算法就可以发挥作用了！于是我们考虑使用 Gibbs Sampling 算法对这个分布进行采样。由于 $\vec{w}$ 是观测数据，只有 $\vec{z}$ 是隐含变量，所以我们真正需要采样的是分布 $p(\vec{z}|\vec{w})$ 。

语料库 $\vec{z}$ 中的第 $i$ 个词对应的 topic 我们记为 $z_i$ ，其中 $i = (m,n)$ 是一个二维下标，对应于第 $m$ 篇文档的第 $n$ 个词，我们用 $\check{i}$ 表示去除下标为 $i$ 的词。那么按照 Gibbs Sampling 算法的要求，我们要求得到任意一个坐标轴 $i$ 对应的条件分布 $p(z_i = k | \vec{z}_{\check{i}},\vec{w})$ 。

假设已经观测到的词 $w_i = t$ ，则由贝叶斯法则，我们容易得到

$p(z_i = k | \vec{z}_{\check{i}},\vec{w}) \approx p(z_i = k,w_i = t | \vec{z}_{\check{i}},\vec{w}_{\check{i}})$

由于 $z_i = k,w_i = t$ 只涉及到第 $m$ 篇文档和第 $k$ 个 topic，去掉第 $i$ 个词对应的 $(z_i,w_i)$ ，并不改变其他文档的 Dirichlet-Multinomial 共轭结构，只是某些地方的计数会减少。

所以 $\vec{\theta}_m,\vec{\varphi}_k$ 的后验分布都是 Dirichlet：

$p(\vec{\theta}_m | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) = Dir(\vec{\theta}_m | \vec{n}_{m,\check{i}} + \vec{\alpha}) \\ p(\vec{\varphi}_k | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) = Dir(\vec{\varphi}_k | \vec{n}_{k,\check{i}} + \vec{\beta})$

我们整理一下，可得到 Gibbs Sampling 公式的推导：

$\begin{array} & p(z_i = k | \vec{z}_{\check{i}},\vec{w}) &\approx& p(z_i = k,w_i = t | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) \\&=& \int p(z_i = k,w_i = t,\vec{\theta}_m,\vec{\varphi}_k | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) d_{\vec{\theta}_m} d_{\vec{\varphi}_k} \\&=& \int p(z_i = k | \vec{\theta}_m)p(\vec{\theta}_m | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) \cdot p(w_i = t | \vec{\varphi}_k)p(\vec{\varphi}_k | \vec{z}_{\check{i}},\vec{w}_{\check{i}}) d_{\vec{\theta}_m} d_{\vec{\varphi}_k} \\&=& \int p(z_i = k | \vec{\theta}_m) Dir(\vec{\theta}_m | \vec{n}_{m,\check{i}} + \vec{\alpha}) d_{\vec{\theta}_m} \\&\cdot& \int p(w_i = t|\vec{\varphi}_k) Dir(\vec{\varphi}_k | \vec{n}_{k,\check{i}} + \vec{\beta}) d_{\vec{\varphi}_k} \\&=& \int \theta_{mk} Dir(\vec{\theta}_m | \vec{n}_{m,\check{i}} + \vec{\alpha}) d_{\vec{\theta}_m} \cdot \int \varphi_{kt} Dir(\vec{\varphi}_k | \vec{n}_{k,\check{i}} + \vec{\beta}) d_{\vec{\varphi}_k} \\&=& E(\theta_{mk}) \cdot E(\varphi_{kt}) \\&=& \hat{\theta}_{mk} \cdot \hat{\varphi}_{kt} \end{array}$

上式看起来复杂，其实是两个独立的过程，每个过程应用 Dirichlet-Multinomail 共轭。

最终得到的 $\hat{\theta}_{mk} , \hat{\varphi}_{kt}$ 就是对应的两个 Dirichlet 后验分布在贝叶斯框架下的参数估计，我们知道：

$\hat{\theta}_{mk} = \frac{n_{m,\check{i}}^{(k)} + \alpha_k}{\sum_{k=1}^K (n_{m,\check{i}}^{(t)} + \alpha_k)} \\ \hat{\varphi}_{kt} = \frac{n_{k,\check{i}}^{(t)} + \beta_t}{\sum_{t=1}^V (n_{k,\check{i}}^{(t)} + \beta_t)}$

于是，我们最终得到了 LDA 模型的 Gibbs Sampling 公式：

$p(z_i = k | \vec{z}_{\check{i}},\vec{w}) \approx \frac{n_{m,\check{i}}^{(k)} + \alpha_k}{\sum_{k=1}^K (n_{m,\check{i}}^{(t)} + \alpha_k)} \cdot \frac{n_{k,\check{i}}^{(t)} + \beta_t}{\sum_{t=1}^V (n_{k,\check{i}}^{(t)} + \beta_t)}$

LDA 模型的优雅之处在于推导的过程中，用gamma函数换掉了积分，同时分子分母利用阶乘的性质而约去，使得最后的结果非常简洁。

这一小节摘录至《LDA数学八卦》，同时在《LDA漫游指南》3.4节中有非常详细的推导过程

Train and Inference

有了 LDA 模型，我们的目标有两个：

估计模型中的参数 $\vec{\varphi}_1,\cdots,\vec{\varphi}_K$ 和 $\vec{\theta}_1,\cdots,\vec{\theta}_M$ ；
对于新来的一篇文档 $doc_{new}$ ，我们能够计算这篇文档的 topic 分布 $\vec{\theta}_{new}$ .

有了 Gibbs Sampling 公式，基于训练语料，训练的流程如下：

随机初始化：对语料中每篇文档中的每个词 $w$ ，随机的赋一个 topic 编号 $z$ ；
重新扫描语料库，对每个词 $w$ ，按照 Gibbs Sampling 公式重新采样它的 topic，在语料中进行更新；
重复以上语料库的采样过程，直到 Gibbs Sampling 收敛；
统计语料库的 topic-word 共现频率矩阵，该矩阵就是 LDA 的模型；

有了训练好的 LDA 模型，当新来一篇文档时，我们可以如下计算 topic 语义分布：

随机初始化：对当前文档中的每个词 $w$ ，随机的赋一个 topic 编号 $z$ ；
重新扫描当前文档，按照 Gibbs Sampling 公式，对每个词 $w$ ，重新采样它的 topic；
重复以上过程直到 Gibbas Sampling 收敛；
统计文档中的 topic 分布，该分布就是 $\vec{\theta}_{new}$

记住，inference过程基本与training过程一致，但在inference过程中，Gibbs Sampling 公式中的主题-词分布 $\vec{\varphi}_{kt}$ 部分是稳定不变的，是由训练语料得到的模型提供的.

主题数选取

上述篇章基本就把 LDA模型大致过了一遍，但有个问题就是主题数 $K$ 还不好选取， $K$ 值取小了，则训练出来的主题之间会有语义上的重叠，若取大了，首先是训练就比较耗时，主题分布会比较稀疏。所以对于一个语料集来说在训练前 $K$ 设为多少合适呢？

尽管到现在也还没有一个非常好的方法可以有效的选取合适的 $K$ 值，有人就用测试语料的困惑度(perplexity)来不断的试验，从而得到比较好的 $K$ ；同时也有人提出了一些比较复杂的模型自适应调节选取合适的主题数 $K$ ，比如 HDP 模型。也有人类比 k-mean 聚类的 $K$ 值的选取，基于密度的自适应调节来得到合适的主题数，这种模型相对简单些，理解和实现起来都比较容易，所以本篇主要介绍这种。

下面介绍 《一种基于密度的自适应最优LDA模型选择方法》-曹娟 的论文中提到的方法：

定义 1(主题密度)：
对给定的主题 $z$ 和距离 $Radius$ ，以 $z$ 为中心，半径为 $Radius$ 画一个圆，分别计算 $z$ 与其它主题之间的相似度（余弦相似度），相似度的值落在圆内的主题数目称为 $z$ 基于 $Radius$ 的密度，记为 $Density(z,Radius)$ .
定义 2(模型基数)：
给定一个主题模型 $M$ 和正整数 $n$ ，模型中密度小于或等于 $n$ 的主题数目称为该模型的基数，记为 $Cardinality(M,n)$ .
定义 3(参考样本)：
对于主题分布中的一个点 $z$ 、距离半径 $r$ 和阈值 $n$ ，如果满足 $Density(z,r) \leq n$ ，则称 $z$ 代表的词空间向量位主题 $z$ 的一个参考样本.

参考样本不是实际数据集中的一个文档向量，而是词空间分布上的一个虚拟点.

主题 $z_i,z_j$ 之间的相似度为:

$corre(z_i,z_j) = \frac{\sum_{v=0}^V z_{iv} \cdot z_{jv}}{\sqrt{\sum_{v=0}^V (z_{iv})^2 \sum_{v=0}^V (z_{jv})^2}}$

$corre(z_i,z_j)$ 越小，主题之间越独立；

所有主题之间的平均相似度来度量该主题结构的稳定性：

$avg\_corre(structure) = \frac{\sum_{i=1}^{K-1}\sum_{j=i+1}^K corre(z_i,z_j)}{K \times (K-1)/2}$

当主题结构的平均相似度最小时，对应的模型最优.

在以上定义的基础上，基于密度的最优模型选择算法可描述为以下过程：

根据任意给定的初始 $K$ 值，以随机抽样方式对 Dirichlet 分布的完全统计矩阵进行初始化，得到一个初始模型 $LDA(\alpha,\beta)$ ；
将初始模型的主题分布矩阵 $\varphi$ 作为一个初始聚类结果，计算所有主题之间的相似度矩阵和平均相似度 $r = avg\_corre(\varphi)$ ，基于 $r$ 得到所有主题的密度 $Density(z,r)$ ，最后，设 $n = 0$ ，计算该模型 $M$ 的基数 $C = Cardinality(M,0)$ ；
根据上步的参考 $K$ 值重新估计 LDA 模型参数， $K$ 的更新函数为:
$K_{n+1} = K_n + f(r) \times (K_n - C_n)$
其中 $f(r)$ 表示 $r$ 的变化方向，当 $r$ 的变化方向为负时（与前一次相反）， $f_{n+1}(r) = -1 \times f_n(r)$ ；当 $r$ 的变化方向为正时（与前一次相同）， $f_{n+1}(r) = f_n(r)$ ； $f_0(r) = -1$

当 $f(r) = -1$ 时，将主题从小到大按密度排序，将前 $C$ 个主题视为参考样本，对下一次 LDA 模型参考估计的 Dirichlet 完全统计矩阵进行初始化；反之采用从集合中抽样的方式对完全矩阵进行初始化；

反复执行第 2 步、第 3 步，直到平均相似度 $r$ 和参数 $K$ 同时收敛。

由于平均相似度最小时主题结构最优，则每次迭代使得 $r$ 减小的方向为正方向.

该论文中的第 2 步感觉是有问题的，首先为什么是以主题的平均相似度为半径计算所有主题的密度 density(z,r) ，按照定义这个密度应该是 " $\epsilon$ - 领域"内的主题数量。

另外为什么要设置 $n = 0$ 来计算模型 M 的基数 $C = Cardinality(M,0)$ ；

这两点论文中写的不清不楚。但大致这种思路我们可以借鉴，经过实际项目中实践去调整出合适的方法。

java 源码分析

github 源码地址：https://github.com/NLPchina/ansj_fast_lda

导入该 maven 工程，程序入口为默认包名下的 FileLDATest.java 程序，首先看看主方法：

public static void main(String[] args) throws IOException {
    LDA lda = new LDA(10);
    for (File dir : files) {
        for (File file : dir.listFiles()) {
            //往 LDA 模型训练器中添加语料
            lda.addDoc(file, "gb2312");
        }
    }
    // 训练模型并保存
    lda.trainAndSave("result/cluster", "utf-8");
}

其中添加文本语料核心代码如下：

public void addDoc(String name ,Reader reader) {
    // 分词
    words = analysis.getWords(reader);
    // 将分词结果设置到 LDA模型中，做统计
    ldaAModel.addDoc(name,words);
}

下面看看再 ldaModel 中做了哪些统计：

public void addDoc(String name, List<String> words) {
    //生成一个文档数据结构，并设置主题数
    Doc doc = new Doc(name,topicNum);
    Integer id = null;
    int topicId = 0;
    //统计文档总数
    dCount++;
    for (String string : words) {
        //将单词映射到索引上
        id = vectorMap.get(string);
        if (id == null) {
            id = vCount;
            vectorMap.put(string, vCount);
            //统计单词总数
            vCount++;
        }
        // 对每个单词随机初始化一个主题编号
        topicId = (int) (Math.random() * topicNum);
        // 文档增加向量
        doc.addVector(new Vector(id, topicId));
    }
    docs.add(doc);
}

我们看到，当一篇文档添加到主题模型中时，会更新单词总数和文档总数，并将单词映射到整数索引上。

回到最开始的主方法，接着我们看训练部分：

public void trainAndSave(String modelPath, String charset) throws IOException {
    //利用初始化好的每个单词的主题来填充主题-词矩阵
    fullTopicVector();
    // 迭代收敛
    for (int i = 0; i < iteration; i++) {
        for (Doc doc : docs) {
            //对每个单词(单词 id，主题 id)
            for (Vector vector : doc.vectors) {
                //采样每个单词的主题
                sampleTopic(doc, vector);
            }
        }
    }
    //保存训练好的模型
    saveModel("result", modelPath, charset);
}

一步一步来，fullTopicVector()中也做了一些主题有关的统计：

private void fullTopicVector() {
    //为主题-词矩阵分配内存
    topics = new Topic[topicNum];
    for (int i = 0; i < topics.length; i++) {
        topics[i] = new Topic(vCount);
    }
    for (Doc doc : docs) {
        // 对每篇文档的每个单词
        for (Vector vector : doc.vectors) {
            //统计每个主题中的每个单词出现的次数
            topics[vector.topicId].addVector(vector);
        }
    }
}

每个 Topic 数据结构中 vCount 表示该主题中所有的单词统计次数，vectorIdArray[id] 表示该主题中单词 id 为 id 的单词出现的次数.

// Compute p(z_i = k|z_-i, w) 抽样
protected void sampleTopic(Doc doc, Vector vector) {
    // 单词的主题 id
    int oldTopic = vector.topicId;
    // w_-i
    doc.removeVector(vector);
    // z_-i
    topics[oldTopic].removeVector(vector);
    double[] p = new double[topicNum];
    for (int k = 0; k < topicNum; k++) {
        // topics[k].vectorIdArray[vector.id] 表示 第 k 个主题所对应的单词中，单词 id 为 vector.id 的单词出现的次数
        // doc.topicArray[k] 表示文档 doc 中第 k 个主题所包含的单词数
        // 根据 Gibbs Sampling 公式更新p(z_i = k|z_-i, w)
        p[k] = (topics[k].vectorIdArray[vector.id] + beta) / (topics[k].vCount + vCount * beta) * (doc.topicArray[k] + alpha)
                    / (doc.topicArray.length - 1 + topicNum * alpha);
    }
    // 轮盘赌最后累计使得p[k]是前面所有topic可能性的和
    // 在《LDA漫游指南》中 4.1 节详细讲了这步逻辑
    for (int k = 1; k < topicNum; k++) {
        p[k] += p[k - 1];
    }
    double u = Math.random() * p[topicNum - 1];
    int newTopic;
    for (newTopic = 0; newTopic < topicNum; newTopic++) {
        //一个随机数 小于某一累积和
        if (u < p[newTopic]) {
            break;
        }
    }
    //更新单词的主题
    vector.topicId = newTopic;
    //更新统计量
    topics[newTopic].addVector(vector);
    doc.updateVecotr(vector);
}

基本就是按照上述理论中提到的

整个 LDA 模型训练部分就完了，可以看到实现起来很简单。

最后保存模型时，我们保存的是文档-主题分布 $\theta$ 和主题-词分布 $\varphi$ ，所以对上述训练结果需要做一些计算：

private void saveModel(String iters, String modelPath, String charset) throws IOException {
    //初始化
    double[][] phi = new double[topicNum][vCount];
    double[][] theta = new double[dCount][topicNum];
    //更新 phi,theta 两个分布
    updateEstimatedParameters(phi, theta);
    //保存模型到文件中
    saveModel(iters, phi, theta, modelPath, charset);
}

根据 $\varphi$ 和 $\theta$ 的 Dirichlet 后验概率分布来估计：

protected void updateEstimatedParameters(double[][] phi, double[][] theta) {
    Topic topic = null;
    for (int k = 0; k < topicNum; k++) {
        topic = topics[k];
        for (int v = 0; v < vCount; v++) {
            // 主题 / 单词 模型
            phi[k][v] = (topic.vectorIdArray[v] + beta) / (topic.vCount + vCount * beta);
        }
    }
    Doc doc = null;
    for (int d = 0; d < dCount; d++) {
        doc = docs.get(d);
        for (int k = 0; k < topicNum; k++) {
            // 文档 / 主题 模型
            theta[d][k] = (doc.topicArray[k] + alpha) / (doc.vectors.size() + topicNum * alpha);
        }
    }
}

$\theta_{mat}(doc \rightarrow topic)$

$\theta_{m,k} = \frac{n_{m,k} + \alpha_k}{\sum_{i=1}^K (n_{m,i} + \alpha_i)} = \frac{n_{m,k} + \alpha}{\sum_{i=1}^K n_{m,i} + K \alpha}$
$\varphi_{mat}(topic \rightarrow word)$

$\varphi_{k,w} = \frac{n_{k,w} + \beta_w}{\sum_{i=1}^V (n_{k,i} + \beta_i)} = \frac{n_{k,w} + \beta}{\sum_{i=1}^V n_{k,i} + V \beta}$

测试过程与训练过程类似，只是主题-词分布稳定不变，其他过程都一样，这里就不多说了。

小结

LDA 主题模型涉及到的数学知识比较多，也比较难理解，笔者也是看了挺多资料才懂，不过该模型的实现很简单，并且在《LDA漫游指南》中也将了基于分布式平台的模型训练方法，在实际项目中也很有帮助。

虽然理解起来比较困难，但多看几遍还是比较清楚的。其中关于主题数的自适应选取，笔者实现一版后再继续更新本文档。

参考

http://www.360doc.com/content/16/0428/10/478627_554452907.shtml
http://www.cnblogs.com/pinard/p/6805861.html
《LDA 数学八卦》
《LDA漫游指南》
《一种基于密度的自适应最优LDA模型选择方法》