时间序列篇

平稳序列建模

建模步骤

假如某个观察值序列通过序列预处理可以判定为平稳非白噪声序列，就可以利用ARMA模型对该序列建模.建模的基本步骤如下:

1. 求出该观察值序列的样本自相关系数(ACF)和样本偏自相关系数(PACF)
2. 根据样本自相关系数和偏自相关系数的性质，选择适当阶数的 $ARMA(p,q)$ 的值
3. 估计模型中未知参数的值
4. 检验模型的有效性.如果拟合模型未通过检验，回到步骤2，重新选择模型拟合
5. 模型优化.如果拟合模型通过检验，任然回到步骤2，充分考虑各种可能，建立多个拟合模型，从所有通过检验的拟合模型中选择最优模型
6. 利用拟合模型，预测序列将来的走势

---

样本自相关系数与偏自相关系数

我们是通过考察平稳序列样本自相关系数和偏自相关系数的性质选择合适的模型拟合观察值序列的，所以模型拟合的第一步是要根据观察值序列的取值求出该序列的样本自相关系数 $\{\hat{\rho}_k,0 < k < n\}$ 和样本偏自相关系数 $\{\hat{\phi}_{kk}, 0 < k < n \}$ 的值.

样本自相关系数可以通过如下公式求得:

$$\hat{\rho}_k = \frac{\sum_{t=1}^{n-k}{(x_t - \overline{x})(x_{t+k} - \overline{x})}}{\sum_{t=1}^n{(x_t - \overline{x})^2}}, \forall 0 < k < n$$

样本偏自相关系数可以利用样本自相关系数的值，根据以下公式求得:

$$\hat{\phi}_{kk} = \frac{\hat{D}_k}{\hat{D}}, \forall 0 < k < n$$ 式中 $$\hat{D} = \left| \begin{matrix} 1 & \hat{\rho}_1 & \cdots & \hat{\rho}_{k-1} \\ \hat{\rho}_1 & 1 & \cdots & \hat{\rho}_{k-2} \\ \vdots & \vdots & & \vdots \\ \hat{\rho}_{k-1} & \hat{\rho}_{k-2} & \cdots & 1 \end{matrix} \right| \\\\ \hat{D}_k = \left| \begin{matrix} 1 & \hat{\rho}_1 & \cdots & \hat{\rho}_1 \\ \hat{\rho}_1 & 1 & \cdots & \hat{\rho}_2 \\ \vdots & \vdots & & \vdots \\ \hat{\rho}_{k-1} & \hat{\rho}_{k-2} & \cdots & \hat{\rho}_k \end{matrix} \right|$$

---

模型识别

计算出样本自相关系数和偏自相关系数的值后，就要根据他们表现出来的性质，选择适当的 $ARMA(p,q)$ 模型拟合观察值序列

这个过程实际上就是要根据样本自相关系数和偏自相关系数的性质估计自相关阶数 $\hat{\rho}$ 和移动平均阶数 $\hat{\rho}$ ，因此，模型识别过程也称为模型定阶过程

$ARMA$模型定阶的基本原则表:

$\hat{\rho}_k$	$\hat{\phi}_{kk}$	模型定阶
拖尾	$p$ 阶截尾	$AR(p)$ 模型
$q$ 阶截尾	拖尾	$MA(q)$ 模型
拖尾	拖尾	$ARMA(p,q)$ 模型

---

但是在实践中，这个定阶原则在操作上具有一定的困难.由于样本的随机性，样本的相关系数不会呈现出理论截尾的完美情况，本应截尾的样本自相关系数或偏自相关系数任会呈现出小值振荡.同时，由于平稳时间序列通常都具有短期相关性，随着延迟阶数 $k \rightarrow \infty,\hat{\rho}_k$与$\hat{\phi}_{kk}$ 都会衰减至零值附近做小值波动.

这种现象促使我们必须思考，当样本自相关系数或偏自相关系数在延迟若干阶之后衰减为小值波动时，什么情况下该看作相关系数截尾，什么情况下该看作相关系数在延迟若干阶之后正常衰减到零值附近做拖尾波动呢?

这实际上没有绝对的标准，很大程度上依靠分析人员的主观经验.但样本自相关系数和偏自相关系数的近似分布可以帮助缺乏经验的分析人员作出尽量合理的判断

---

Jankins 和 Watts 于 1968年证明:

$$E(\hat{\rho}_k) = \left( 1 - \frac{k}{n} \right) \rho_k$$ 也就是说，该样本自相关系数是总体自相关系数的有偏估计,当 $k$ 足够大时，根据平稳序列自相关系数呈负指数衰减，有 $\rho_k \rightarrow 0$

根据 Bartlett 公式计算样本自相关系数的方差:

$$Var(\hat{\rho}_k) \approx \frac{1}{n} \sum_{m=-j}^j{\hat{\rho}_m^2} = \frac{1}{n} \left( 1 + 2 \sum_{m=1}^j{\hat{\rho}_m^2} \right)$$ 当样本容量 $n$ 充分大时，样本自相关系数近似服从正态分布: $$\hat{\rho}_k \hat{=} N \left( 0, \frac{1}{n} \right)$$
Quenouille 证明，样本偏自相关系数也同样近似服从这个正态分布: $$\hat{\phi}_{kk} \hat{=} N \left( 0, \frac{1}{n} \right)$$ 根据正态分布的性质，有 $$Pr\left( -\frac{2}{\sqrt{n}} \leq \hat{\rho}_k \leq \frac{2}{\sqrt{n}} \right) \geq 0.95 \\ Pr\left( -\frac{2}{\sqrt{n}} \leq \hat{\phi}_{kk} \leq \frac{2}{\sqrt{n}} \right) \geq 0.95$$ 所以可以利用 $2$ 倍标准差范围辅助判断.

如果样本自相关系数或偏自相关系数在最初的 $d$ 阶明显超过 $2$ 倍标准差范围，而后几乎 $95\%$ 的自相关系数都落在 $2$ 倍标准差的范围以内，而且由非零自相关系数衰减为小值波动的过程非常突然，这时，通常视为自相关系数截尾，截尾阶数为 $d$

如果有超过 $5\%$ 的样本自相关系数落入 $2$ 倍标准差范围之外，或者由显著非零的自相关系数衰减为小值波动的过程比较缓慢或者非常连续，这时，通常视为自相关系数不截尾.

R程序演示模型识别

> a <- read.table("data/file8.csv",sep = ",", header = T)
> x <- ts(a$kilometer, start = 1950)
> plot(x)

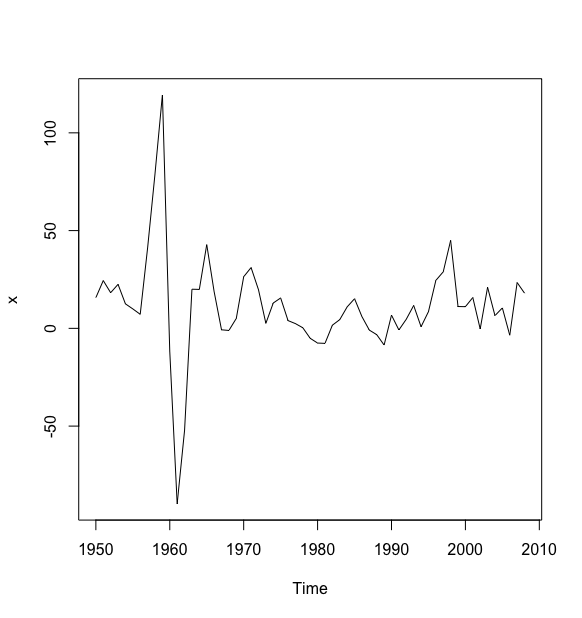
时序图可以看成，序列没有显著非平稳特征.

#白噪声检验
> for(i in 1:2) print(Box.test(x, type = "Ljung-Box", lag = 6*i))
    Box-Ljung test
data:  x
X-squared = 37.754, df = 6, p-value = 1.255e-06
    Box-Ljung test
data:  x
X-squared = 44.62, df = 12, p-value = 1.197e-05
> 

白噪声检验显示序列值彼此之间蕴涵着相关关系，为非白噪声序列.

> acf(x)

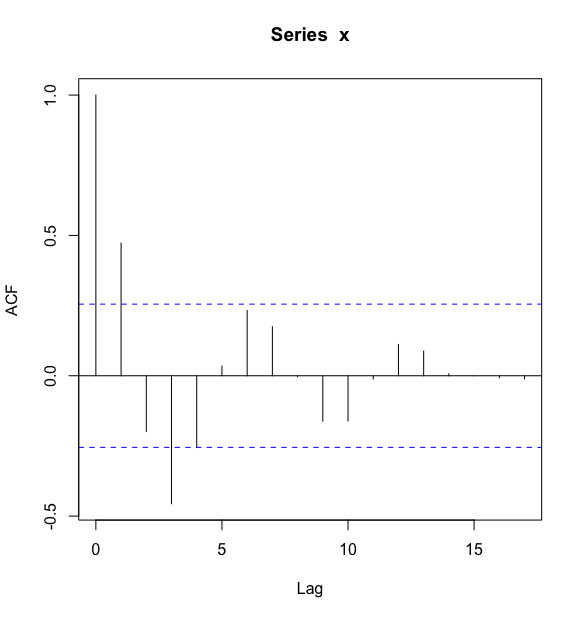
自相关系数图可以看出，除了延迟 1~3 阶的自相关系数在 2 倍标准差范围之外，其他阶数的自相关系数都在 2 倍标准差范围内波动.根据自相关系数的这个特点可以判断该序列具有短期相关性，进一步确定序列平稳.

在进一步考察自相关系数衰减到零的过程，可以看到有明显的正弦波动轨迹，这说明自相关系数衰减到零不是一个突然的过程，而是一个连续渐变的过程，这是自相关系数拖尾的典型特征，我们可以把拖尾特征形象的描述为“坐着滑梯落水”.

> pacf(x)
> 

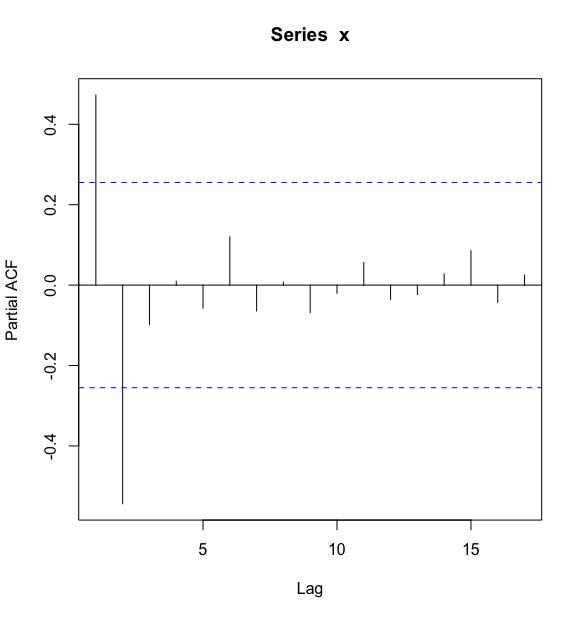
最后考察偏自相关系数衰减到零的过程，除了 1~2 阶偏自相关系数在 2 倍标准差范围之外，其他阶数的偏自相关系数都在 2 倍标准差范围内，这是一个偏自相关系数 2 阶截尾的典型特征，我们可以把这种截尾特征形象地描述为“2 阶之后高台跳水”.

本例中，根据自相关系数拖尾，偏自相关系数 2 阶截尾属性，可以初步确定拟合模型为 $AR(2)$ 模型.

---

参数估计

选择好拟合模型之后，下一步就是要利用序列的观察值确定该模型的参数值.

对于一个非中心化 $ARMA(p,q)$ 模型，有

$$x_t = \mu \frac{\Theta_q(B)}{\Phi_p(B)} \epsilon_t$$ 式中 $$\epsilon_t \approx W N(0,\sigma_{\epsilon}^2) \\ \Theta_q(B) = 1 - \theta_1 B - \cdots - \theta_q B^q \\ \Phi_p(B) = 1 - \phi_1 B - \cdots - \phi_p B^p$$ 该模型共含有 $p+q+2$ 个未知参数: $\phi_1 ,\cdots,\phi_p,\theta_1,\cdots,\theta_q,\mu,\sigma_{\epsilon}^2$

---

参数 $\mu$ 是序列均值，通常采用矩估计法，用样本均值估计总体均值即可:

$$\hat{\mu} = \overline{x} = \frac{\sum_{i=1}^n{x_i}}{n}$$ 对原序列中心化，则有 $$y_t = x_t - \overline{x}$$ 原 $p+q+2$ 个待估参数减少为 $p+q+1$ 个: $\phi_1 ,\cdots,\phi_p,\theta_1,\cdots,\theta_q,\sigma_{\epsilon}^2$，对这 $p+q+1$ 个未知参数的估计方法有三种: 矩估计、极大似然估计和最小二乘估计.

---

矩估计

运用 $p+q$ 个样本自相关系数估计总体自相关系数

$$\begin{cases} \rho_1(\phi_1 ,\cdots,\phi_p,\theta_1,\cdots,\theta_q) = \hat{\rho}_1 \\ \vdots \\ \rho_{p+q}(\phi_1 ,\cdots,\phi_p,\theta_1,\cdots,\theta_q) = \hat{\rho}_{p+q} \end{cases}$$ 从中解出的参数值 $\hat{\phi}_1, \cdots, \hat{\phi}_p,\hat{\theta}_1,\cdots,\hat{\theta}_q$ 就是 $\phi_1,\cdots,\phi_p,\theta_1,\cdots,\theta_q$ 的矩估计.

用序列样本方差估计序列总体方差:

$$\hat{\sigma_x^2} = \frac{\sum_{i=1}^n{(x_i - \overline{x})^2}}{n}$$ 在 $ARMA(p,q)$ 模型两边同时求方差，整理得到 $\sigma_{\epsilon}^2$ 关于 $\sigma_{\epsilon}^2$ 的函数形式 $$\sigma_{\epsilon}^2 = \frac{1+\phi_1^2 + \cdots + \phi_p^2}{1+\theta_1^2 + \cdots + \theta_q^2} \sigma_{x}^2$$ 把 $\hat{\phi}_1, \cdots, \hat{\phi}_p,\hat{\theta}_1,\cdots,\hat{\theta}_q$ 及 $\hat{\sigma}_x^2$ 代入上式，即得到白噪声序列方差的矩估计: $$\sigma_{\epsilon}^2 = \frac{1+\hat{\phi}_1^2 + \cdots + \hat{\phi}_p^2}{1+\hat{\theta}_1^2 + \cdots + \hat{\theta}_q^2} \sigma_{x}^2$$

矩估计方差，尤其是低阶 $ARMA$ 模型场合下的矩估计方法具有计算量小、估计思想简单直观，且不需要假设总体分布的优点.但是在这种估计方法中只用到了 $p+q$ 个样本自相关系数，即样本二阶矩的信息，观察值序列中的其他信息都被忽略了.这导致矩估计方法是一种比较粗糙的估计方法，它的估计精度一般不高，因此它常用作确定极大似然估计和最小二乘估计迭代计算的初始值.

---

极大似然估计

在极大似然准则下，认为样本来自使该样本出现概率最大的总体.因此未知参数的极大似然估计就是使得似然函数(即联合密度函数)达到最大的参数值.

$$L(\hat{\beta}_1,\hat{\beta}_2,\cdots,\hat{\beta}_k;x_1,x_2,\cdots,x_n) = max\{p(x_1,x_2,\cdots,x_n);\beta_1,\beta_2,\cdots,\beta_k\}$$
使用极大似然估计必须已知总体的分布函数，而在实际序列分析中，序列总体的分布通常是未知的.为便于分析和计算，通常假设序列服从多元正态分布.
$$x_t = \phi_1 x_{t-1} + \cdots + \phi_p x_{t-p} + \epsilon_t - \theta_1 \epsilon_{t-1} - \cdots - \theta_q \epsilon_{t-q}$$
记 $$\hat{\boldsymbol{x}} = (x_1,\cdots,x_n) \\ \hat{\boldsymbol{\beta}} = (\phi_1,\cdots,\phi_p,\theta_1,\cdots,\theta_q)' \\ \boldsymbol{\sum}_n = E(\hat{x}' \hat{x}) = \boldsymbol{\Omega} \sigma_{\epsilon}^2$$ 式中 $$\boldsymbol{\Omega} = \left( \begin{matrix} \sum_{i=0}^{\infty}{G_i^2} & \cdots & \sum_{i=0}^{\infty}{G_i G_{i+n-1}} \\ \vdots & \ddots & \vdots \\ \sum_{i=0}^{\infty}{G_i G_{i+n-1}} & \cdots & \sum_{i=0}^{\infty}{G_i^2} \end{matrix} \right)$$
$\hat{\boldsymbol{x}}$ 的似然函数为: $$L(\hat{\boldsymbol{\beta}};\hat{\boldsymbol{x}}) = p(x_1,x_2,\cdots,x_n;\hat{\boldsymbol{\beta}}) \\ = (2 \pi)^{-\frac{n}{2}} \left| \sum_n \right|^{\frac{1}{2}} exp\{- \frac{\hat{\boldsymbol{x}}' \sum_n^{-1} \hat{\boldsymbol{x}} }{2}\} \\ = (2 \pi)^{-\frac{n}{2}} (\sigma_{\epsilon}^2)^{-\frac{n}{2}} |\boldsymbol{\Omega}|^{-\frac{1}{2}} exp\{ - \frac{\hat{\boldsymbol{x}}' \boldsymbol{\Omega}^{-1} \hat{\boldsymbol{x}} }{2 \sigma_{\epsilon}^2} \}$$
对数似然函数为: $$l(\hat{\boldsymbol{\beta}}; \hat{\boldsymbol{x}}) = -\frac{n}{2} ln(2 \pi) - \frac{n}{2} ln(\sigma_{\epsilon}^2) -\frac{1}{2} ln|\boldsymbol{\Omega}| - \frac{1}{2 \sigma_{\epsilon}^2} \left[ \hat{\boldsymbol{x}}' \boldsymbol{\Omega}^{-1} \hat{\boldsymbol{x}} \right]$$
对对数似然函数中的未知参数求偏导数，得到似然方程组:
$$\begin{cases} \frac{\partial}{\partial \sigma_{\epsilon}^2} l(\hat{\boldsymbol{\beta}};\hat{\boldsymbol{x}}) = - \frac{n}{2 \sigma_{\epsilon}^2} + \frac{S(\hat{\boldsymbol{\beta}})}{2 \sigma_{\epsilon}^4} = 0 \\ \frac{\partial}{\partial \hat{\boldsymbol{\beta}}} l(\hat{\boldsymbol{\beta}};\hat{\boldsymbol{x}}) = - \frac{1}{2} \frac{\partial ln|\boldsymbol{\Omega}|}{\partial \hat{\boldsymbol{\beta}}} - \frac{1}{\sigma_{\epsilon}^2} \frac{\partial S(\hat{\boldsymbol{\beta}})}{2 \partial \hat{\boldsymbol{\beta}}} = 0 \end{cases}$$ 式中，$S(\hat{\boldsymbol{\beta}}) = \hat{\boldsymbol{x}}' \boldsymbol{\Omega}^{-1} \hat{\boldsymbol{x}}$

理论上，求解方程组即得到未知参数的极大似然估计值.但是由于 $S(\hat{\boldsymbol{\beta}})$ 和 $ln|\boldsymbol{\Omega}|$ 都不是 $\hat{\boldsymbol{\beta}}$ 的显示表达式的，因此似然方程组实际上是由 $p+q+1$ 个超越方程构成的，通常需要经过复杂的迭代算法才能求出未知参数的极大似然估计值.

---

最小二乘估计

在 $ARMA(p,q)$ 模型场合，记

$$\hat{\boldsymbol{\beta}} = (\phi_1,\cdots,\phi_p, \theta_1,\cdots,\theta_q)' \\ F_t(\hat{\boldsymbol{\beta}}) = \phi_1 x_{t-1} + \cdots + \phi_p x_{t-p} - \theta_1 \epsilon_{t-1} - \cdots - \theta_q \epsilon_{t-q}$$ 残差项为: $$\epsilon_t = x_t - F_t(\hat{\boldsymbol{\beta}})$$ 残差平方和为: $$Q(\hat{\boldsymbol{\beta}}) = \sum_{t=1}^n \epsilon_t^2 \\= \sum_{t=1}^n (x_t - \phi_1 x_{t-1} - \cdots - \phi_p x_{t-p} + \theta_1 \epsilon_{t-1} + \cdots + \theta_q \epsilon_{t-q})^2$$ 使残差平方和达到最小的那组参数值即为 $\hat{\boldsymbol{\beta}}$ 的最小二乘估计值.

---

由于随机扰动 $\epsilon_{t-1}, \epsilon_{t-2},\cdots$ 不可观测，所以 $Q(\hat{\boldsymbol{\beta}})$ 也不是 $\hat{\boldsymbol{\beta}}$ 的显性函数，未知参数的最小二乘估计值通常也得借助迭代法求出.由于充分利用了序列观测值的信息，因此最小二乘法估计的精度很高.

在实际运用中，最常用的是条件最小二乘估计方法.它假定过去未观测到的序列值等于零，即

$$x_t = 0, t \leq 0$$ 根据这个假定可以得到残差序列的有限项表达式: $$\epsilon_t = \frac{\Phi(B)}{\Theta(B)} x_t = x_t - \sum_{i=1}^t {\pi_i x_{t-i}}$$ 于是残差平方和为: $$Q(\hat{\boldsymbol{\beta}}) = \sum_{i=1}^n \epsilon_t^2 = \sum_{i=1}^n {\left[ x_t - \sum_{i=1}^t{\pi_i x_{t-i}} \right]^2}$$ 通过迭代法，使上式达到最小值的估计值即为参数 $\boldsymbol{\beta}$ 的条件最小二乘估计.

---

模型检验

确定模型参数后，我们还要对该拟合模型进行必要的检验.

模型的显著性检验

模型的显著性检验主要是检验模型的有效性.一个模型是否显著有效主要看它提取的信息是否充分.一个好的拟合模型应该能够提取观察值序列中几乎所有的样本相关信息，换言之，拟合残差项中将不再蕴涵任何相关信息，即残差序列应该为白噪声序列.这样的模型称为显著有效模型.

反之，如果残差序列为非白噪声序列，那就意味着残差序列中还残留着相关信息未被提取，这就说明拟合模型不够有效，通常需要选择其他模型，重新拟合.

所以模型的显著性检验即为残差序列的白噪声检验.

---

原假设和备择假设分别为:

$$H_0 : \rho_1 = \rho_2 = \cdots = \rho_m = 0, \forall m \geq 1 \\ H_1 : 至少存在某个 \rho_k \neq 0, \forall m \geq 1, k \leq m$$
检验统计量为 $LB(Ljung-Box)$ 检验统计量: $$LB = n(n+2) \sum_{k=1}^m \left( \frac{\hat{\rho}_k^2}{n - k} \right) \approx \chi^2(m), \forall m > 0$$
如果拒绝原假设，就说明残差序列中还残留着相关信息，拟合模型不显著.如果不能拒绝原假设，就认为拟合模型显著有效.

---

以1950-2008年我国邮路及农村投递路线每年新增里程数序列来拟合模型的显著性 ($\alpha = 0.05$) 为例，演示R代码的使用:

> a <- read.table("data/file8.csv",sep = ",", header = T)
> x <- ts(a$kilometer, start = 1950)
> x.fit <- arima(x,order = c(2,0,0), method = "ML")
> for(i in 1:2) print(Box.test(x.fit$residual,lag = 6*i))
    Box-Pierce test
data:  x.fit$residual
X-squared = 2.0949, df = 6, p-value = 0.9108
    Box-Pierce test
data:  x.fit$residual
X-squared = 2.8341, df = 12, p-value = 0.9966
>

由于各阶延迟下 $LB$ 统计量的 $P$ 值都显著大于 0.05，可以认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效.

---

参数的显著性检验

参数的显著性检验就是要检验每一个未知参数是否显著非零.这个检验的目的是使模型最精简.

如果某个参数不显著，即表示该参数所对应的那个自变量对因变量的影响不明显，该自变量可以从拟合模型中剔除.最终模型将由一系列参数显著非零的自变量表示.

---

检验假设:

$$H_0 : \beta_j = 0 \\ H_1 : \beta_j \neq 0 , \forall 1 \leq j \leq m \\ E(\hat{\boldsymbol{\beta}}) = E\left[ (\boldsymbol{X}'\boldsymbol{X})^{-1} \boldsymbol{X}' \hat{\boldsymbol{y}} \right] = \boldsymbol{X}'\boldsymbol{X})^{-1} \boldsymbol{X}' \hat{\boldsymbol{y}} = \hat{\boldsymbol{\beta}} \\ Var(\hat{\boldsymbol{\beta}}) = Var \left[ (\boldsymbol{X}'\boldsymbol{X})^{-1} \boldsymbol{X}' \hat{\boldsymbol{y}} \right] = (\boldsymbol{X}'\boldsymbol{X})^{-1} \boldsymbol{X}'\boldsymbol{X} (\boldsymbol{X}'\boldsymbol{X})^{-1} \sigma_{\epsilon}^2 \\ = (\boldsymbol{X}'\boldsymbol{X})^{-1} \sigma_{\epsilon}^2$$ 对于线性拟合模型，记 $\hat{\boldsymbol{\beta}}$ 为 $\boldsymbol{\beta}$ 的最小二乘估计，有 $$\boldsymbol{\Omega} = (\boldsymbol{X}'\boldsymbol{X})^{-1} = \left( \begin{matrix} a_{11} & \cdots & a_{1m} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mm} \end{matrix} \right)$$
在正态分布假定下，第 $j$ 个未知参数的最小二乘估计值 $\hat{\beta}_j$ 服从正态分布: $$\hat{\beta}_j \approx N(0, a_{jj} \sigma_{\epsilon}^2) , 1 \leq j \leq m$$ 由于 $\sigma_{\epsilon}^2$ 不可观测，用最小残差平方和估计 $\sigma_{\epsilon}^2$: $$\hat{\sigma}_{\epsilon}^2 = \frac{Q(\hat{\boldsymbol{\beta}})}{n-m}$$ 根据正态分布的性质，有 $$\frac{Q(\hat{\boldsymbol{\beta}})}{\sigma_{\epsilon}^2} \approx \chi^2(n-m)$$ 由上两式可以构造出用于检验未知参数显著性的 $t$ 检验统计量 $$t = \sqrt{n-m} \frac{\hat{\beta}_j}{\sqrt{a_{jj} Q(\hat{\boldsymbol{\beta}})}} \approx t(n-m)$$ 当该检验统计量的绝对值大于自由度为 $n-m$ 的 $t$ 分布的 $1 - \alpha$ 分位点，即 $$|t| \geq t_{1 - \alpha}(n-m)$$ 或者该检验统计量的 $P$值小于 $\alpha$时，拒绝原假设，认为该参数显著；否则，认为该参数不显著.这时，应该剔除不显著参数所对应的自变量重新拟合模型，构造出新的、结构更精炼的拟合模型.

---

R 不提供参数的显著性检验结果，一般默认输出参数均显著非零，如果用户想获得参数检验统计零的 $P$ 值，需要自己计算参数的 $t$ 统计量的值及统计量的 $P$值.

根据 $t$ 统计量的定义，参数估计值除以参数标准差即为该参数的 $t$ 统计量

$$t = \frac{\hat{\phi}_i}{\sigma}$$ 再调用 $t$ 分布 $P$ 值函数 $pt$ 即可获得该统计量的 $P$值.

下面还是以邮路数据为例，演示R程序的参数显著性检验:

> a <- read.table("data/file8.csv",sep = ",", header = T)
> x <- ts(a$kilometer, start = 1950)
> x.fit <- arima(x,order = c(2,0,0), method = "ML")
> x.fit
Call:
arima(x = x, order = c(2, 0, 0), method = "ML")
Coefficients:
         ar1      ar2  intercept
      0.7185  -0.5294    11.0223
s.e.  0.1083   0.1067     3.0906
sigma^2 estimated as 365.2:  log likelihood = -258.23,  aic = 524.46
> t1 <- 0.7185/0.1083
> pt(t1,df=56,lower.tail = F)
[1] 6.94276e-09
> 
> t2 <- -0.5294/0.1067
> pt(t2,df=56,lower.tail = T)
[1] 3.43633e-06
> 
> t0 <- 11.0223/3.0906
> pt(t0,df = 56, lower.tail = F)
[1] 0.0003748601
>

从检验结果看，三个系数均显著非零.

---

模型优化

AIC准则

AIC 准则是由日本统计学家 Akaike 于1973年提出的，它的全称是最小信息准则(Akaike information criterion).

该准则的指导思想是一个拟合模型的优劣可以从两方面去考察:

• 一方面是大家非常熟悉的常用来衡量拟合程度的似然函数值；
• 另一方面是模型中未知参数的个数.

通常似然函数值越大，说明拟合效果越好.模型中未知参数个数越多，说明模型中包含的自变量越多，自变量越多，模型变化越灵活，模型拟合的准确度就会越高.模型拟合程度高是我们所希望的，但是我们又不能单纯的以拟合精度来衡量模型的优劣，因为这样势必会导致未知参数的个数越多越好.

未知参数越多，说明模型中自变量越多，未知的风险越多.而且参数越多，参数估计的难度就越大，估计的精度也就越差.所以一个好的拟合模型应该是拟合精度和未知参数个数的综合最优配置.

---

AIC准则就是在这种考虑下提出的，它是拟合精度和参数个数的加权函数:

$$AIC = -2 ln(模型的极大似然函数值) + 2(模型中未知参数个数)$$ 使 AIC函数 达到最小的模型被认为是最优模型.

在 $ARMA(p,q)$ 模型场合，对数似然函数为:

$$l(\hat{\beta};x_1,\cdots,x_n) = - \left[ \frac{n}{2} ln(\sigma_{\epsilon}^2) + \frac{1}{2} ln |\Omega| + \frac{1}{2 \sigma_{\epsilon}^2 S(\hat{\beta})} \right]$$ 因为 $\frac{1}{2} ln|\Omega|$ 有界， $\frac{1}{2 \sigma_{\epsilon}^2 S(\hat{\beta})} \rightarrow \frac{n}{2}$ ，所以似然函数与 $- \frac{n}{2} ln(\sigma_{\epsilon}^2)$ 成正比.
$$l(\hat{\beta};x_1,\cdots,x_n) \approx - \frac{n}{2} ln(\sigma_{\epsilon}^2)$$ 中心化 $ARMA(p,q)$ 模型的未知参数个数为 $p+q+1$，非中心化 $ARMA(p,q)$ 模型的未知参数个数为 $p+q+2$.

所以，中心化 $ARMA(p,q)$ 模型的 $AIC$ 函数为:

$$AIC = n ln(\hat{\sigma}_{\epsilon}^2) + 2(p+q+1)$$ 非中心化 $ARMA(p,q)$ 模型的 $AIC$函数为: $$AIC = n ln(\hat{\sigma}_{\epsilon}^2) + 2(p+q+2)$$

---

SBC (BIC)准则

AIC 准则为选择最优模型提供了有效的规则，但其也有不足之处.对于一个观察值序列而言，序列越长，相关信息就越分散，要很充分地提取其中的有用信息，或者说要使拟合精度比较高，通常需要包含多个自变量的复杂模型.在 AIC 准则中拟合误差提供的信息要受到样本容量的放大，它等于 $n ln(\hat{\sigma}_{\epsilon}^2)$，但参数个数的惩罚因子却和样本容量没关系，它的权重始终是常数 2. 因此在样本容量趋于无穷大时，由 AIC 准则选择的模型不收敛于真实模型，它通常比真实模型所含的未知参数个数要多.

为了弥补 AIC 准则的不足，Akaike 于 1976年提出了 BIC准则.而 Schwartz 在1978年根据 Bayes理论也得出了同样的判别准则，称为 SBC准则.

SBC准则的定义为:

$$SBC = -2 ln(模型的极大似然函数值) + ln(n)(模型中未知参数个数)$$ SBC对 AIC 的改进就是将未知参数个数的惩罚权重由常数 2 变成了样本容量的对数函数值. 理论上已证明，SBC准则确定的最优模型是真实阶数的相合估计.

---

容易得到，中心化 $ARMA(p,q)$ 模型的 SBC函数为:

$$SBC = n ln(\hat{\sigma}_{\epsilon}^2) + ln(n)(p + q + 1)$$ 非中心化 $ARMA(p,q)$ 模型的 SBC函数为: $$SBC = n ln(\hat{\sigma}_{\epsilon}^2) + ln(n)(p + q + 2)$$

在所有通过检验的模型中使得 AIC 或 SBC函数达到最小的模型为相对最优模型.之所以称为相对最优模型而不是绝对最优模型，是因为我们不可能比较所有模型的 AIC 和 SBC 函数值，我们总是在尽可能全面的范围里考察有限多个模型的 AIC 和 SBC 函数值，在选择其中 AIC 和 SBC 函数值达到最小的那个模型作为最终的拟合模型，因而这样得到的最优模型就是一个相对最优模型.

AIC 准则和 SBC 准则的提出，可以有效弥补根据自相关图和偏自相关图定阶的主观性，在有限的阶数范围内帮助我们寻找相对最优拟合模型.

---

R程序演示