机器学习篇

EM 算法

EM 算法是一种迭代算法，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计.

概率模型有时含有观测变量（observable variable），又含有隐变量或潜在变量（latent variable）.如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或贝叶斯估计法估计模型参数.但是，当模型含有隐变量时，就不能简单地使用这些估计方法. EM 算法就是含有隐变量的概率模型参数的极大似然估计法.

EM 算法的每次迭代由两步组成: E 步，求期望（expectation）；M 步，求极大（maximization）.所以这一算法称为期望极大算法（expectation maximization algorithm），简称 EM 算法.

当然，EM 算法比较复杂，我们会从一个简单的例子入手来逐步深入其原理，及其数学推导，最后用 R 实例的应用来演示如何使用.

---

实例引入

简单实例

假设有两枚硬币 1 和 2，随机抛掷后正面朝上的概率分别为 $P_1,P_2$。为了估计这两个概率，做了如下实验，每次取一枚硬币，连掷 5 下，记录结果如下:

硬币	结果	统计
1	正正反正反	3 正 - 2 反
2	反反正正反	2 正 - 3 反
1	正反反反反	1 正 - 4 反
2	正反反正正	3 正 - 2 反
1	反正正反反	2 正 - 3 反

此时是很容易估计出 $P_1,P_2$ 的，如下:

$$\begin{array} & P_1 &=& \frac{1}{3} \left(\frac{3}{5} + \frac{1}{5} + \frac{2}{5} \right) = 0.4 \\ P_2 &=& \frac{1}{2} \left( \frac{2}{5} + \frac{3}{5} \right) = 0.5 \end{array}$$

此处用到极大似然估计，可参考 https://www.zybuluo.com/evilking/note/963269

---

加入隐变量 $z$

下面加大点难度，还是上面的问题，现在我们抹去每轮投掷时使用的硬币标记，记录结果如下:

硬币	结果	统计
unknown	正正反正反	3 正 - 2 反
unknown	反反正正反	2 正 - 3 反
unknown	正反反反反	1 正 - 4 反
unknown	正反反正正	3 正 - 2 反
unknown	反正正反反	2 正 - 3 反

现在目标没变，还是要估计 $P_1,P_2$，那又该如何做呢？

现在每次投掷的硬币未知，这就无法用上小节这种方法来求，但是若我们能先确定每次投掷的硬币标记，在此前提下就可以用上小节的方法来求解了。

我们假设硬币的标号为隐变量 $z,z \in (1,2)$，我们要估计出 $P_1,P_2$，就得先估计出 $z$，然后用上一小节中的最大似然概率法则来估计出 $P_1,P_2$；但要估计 $z$，我们又得先知道 $P_1,P_2$；这样看似鸡生蛋、蛋生鸡的问题如何破？

我们可以借助迭代提升法的思想来做，比如我们先根据经验初始化一个 $P_1,P_2$，然后按照最大似然概率可以估计出 $z$，然后基于 $z$，再按照最大似然概率反过来估计出 $P_1,P_2$，若此时的 $P_1,P_2$ 比初始值更接近于真实值，那照此方法依次迭代下去，若收敛，最后就能收敛到 $P_1,P_2$ 的真实值.

---

EM 初级版

EM 算法正是按上面的步骤来做的，具体来说，我们不妨先随便给 $P_1,P_2$ 赋一个初值，如:

$$P_1 = 0.2 \\ P_2 = 0.7$$

然后我们先根据 $P_1,P_2$ 按最大似然概率估计第一轮抛掷最可能是哪个硬币:

• 若是硬币 1，得出 3 正 2 反 的概率为 $0.2*0.2*0.2*0.8*0.8 = 0.00512$
• 若是硬币 2，得出 3 正 2 反 的概率为 $0.7*0.7*0.7*0.3*0.3 = 0.03087$

可以看出第一轮抛掷的硬币是 2 的概率大于是硬币 1 的概率，则我们估计第一轮最有可能抛掷的是硬币 2.

按此方法我们依次估计其他轮，结果如下:

轮数	若是硬币 1	若是硬币 2	估计投掷的硬币
1	0.00512	0.03087	2
2	0.02048	0.01323	1
3	0.08192	0.00567	1
4	0.00512	0.03087	2
5	0.02048	0.01323	1

---

我们把上面的值作为 $z$ 的估计值，于是抛掷记录更新为:

估计硬币	结果	统计
2	正正反正反	3 正 - 2 反
1	反反正正反	2 正 - 3 反
1	正反反反反	1 正 - 4 反
2	正反反正正	3 正 - 2 反
1	反正正反反	2 正 - 3 反

然后按照最大似然概率法则反过来估计 $P_1,P_2$ :

$$\begin{array} & P_1 &=& (2+1+2)/15 = 0.33 \\ P_2 &=& (3+3)/10 = 0.6 \end{array}$$

---

此时第一轮迭代结束，假设我们站在上帝视角，已经知道了每轮抛掷时的硬币就如本篇第一小节中标识的那样，那么，$P_1,P_2$ 的最大似然估计就是 $0.4,0.5$（假设就是真实值），那么用真实值与迭代前和迭代后的估计值做比较:

初始化的 $P_1$	估计出的 $P_1$	真实值 $P_1$	初始化的 $P_2$	估计出的 $P_2$	真实值 $P_2$
0.2	0.33	0.4	0.7	0.6	0.5

对比后会发现，迭代后的 $P_1,P_2$ 估计值比初始化的 $P_1,P_2$ 更加接近真实值了.

可以想象，如果按这种迭代思路，我们用最新估计出的 $P_1,P_2$ 再去估计每轮的硬币标号 $z$，然后用 $z$ 再去估计 $P_1,P_2$，如此反复迭代下去，$P_1,P_2$ 最后会保持不变，收敛到真实值，这样我们就找到了 $P_1,P_2$ 的最大似然估计.

在后面的理论部分，我们会证明新估计出的 $P_1,P_2$ 一定会更接近真实的 $P_1,P_2$.

EM 算法是对初值敏感的，所以最后肯定会收敛，但是不一定会收敛到真实值.

---

EM 进阶版

在上面的 EM 初级版本中，我们是用最大似然概率发展估计出的 $z$ 值，然后再用 $z$ 按照最大似然概率法则估计新的 $P_1,P_2$，也就是说，我们仅使用了一个最可能的 $z$ 值，而不是所有可能的 $z$ 值.

如果考虑所有可能的 $z$ 值，对每一个 $z$ 值都估计出一个新的 $P_1,P_2$，将每个 $z$ 值概率大小作为权重，将所有新估计出的 $P_1,P_2$ 分别做加权和，这样得到的 $P_1,P_2$ 应该会更好一些.

考虑所有可能的 $z$ 值，有一定的难度，我们可以用期望来近似:

轮数	若是硬币 1	若是硬币 2
1	0.00512	0.03087
2	0.02048	0.01323
3	0.08192	0.00567
4	0.00512	0.03087
5	0.02048	0.01323

利用上面这个表，我们可以算出每轮投掷中使用硬币 1 或使用硬币 2 的概率，比如第一轮中使用硬币 1 的概率为:

$$p_1 = \frac{0.00512}{0.00512 + 0.03087} = 0.14$$ 使用硬币 2 的概率为: $$p_2 = 1 - 0.14 = 0.86$$

依次计算其他轮，得:

轮数	$z$ 为硬币 1	$z$ 为硬币 2
1	0.14	0.86
2	0.61	0.39
3	0.94	0.06
4	0.14	0.84
5	0.61	0.39

上表中的右两列表示使用硬币 $z$ 的期望值，解释一下，第一轮中的 0.86 表示第一轮使用硬币 2 投掷的概率是 $p(z_2) = 0.86$.

相比于初级版本中我们之间将第一轮估计为使用的硬币 2，此时我们更加的谨慎，我们只是说，有 0.14 的概率使用的是硬币 1，有 0.86 的概率使用的是硬币 2，不再是非此即彼。这样我们在估计 $P_1,P_2$ 时，就可以看成是用上了全部的数据，而不是部分的数据，显然这样会更好一些.

这一步我们实际上是估计出了 $z$ 的概率分布，这步在 EM算法中称作 E 步.

结合下表:

硬币	结果	统计
unknown	正正反正反	3 正 - 2 反
unknown	反反正正反	2 正 - 3 反
unknown	正反反反反	1 正 - 4 反
unknown	正反反正正	3 正 - 2 反
unknown	反正正反反	2 正 - 3 反

我们按照期望最大似然概率的法则来估计新的 $P_1,P_2$ :

以 $P_1$ 的估计为例，第一轮的 3 正 2 反相当于:

$$0.14*3 = 0.42 \quad (正面次数的期望) \\ 0.14*2 = 0.28 \quad (反面次数的期望)$$ 依次算出其他四轮，列表如下:

轮数	正面的期望次数	反面的期望次数
1	0.42	0.28
2	1.22	1.83
3	0.94	3.76
4	0.42	0.28
5	1.22	1.83
总计	4.22	7.98

于是:

$$p_1 = \frac{4.22}{4.22 + 7.98} = 0.35$$

可以看到，改变了 $z$ 值的估计方法后，新估计出的 $P_1$ 要更加接近真实值. 原因就是我们使用了所有抛掷的数据，而不是之前只使用了部分的数据.

这步中，我们根据 E 步中求出的 $z$ 的概率分布，然后依据最大似然概率法则去估计 $P_1,P_2$，被称作 M 步.

Reference: http://pan.baidu.com/s/1i4NfvP7

---

EM 算法

下面我们根据上面的例子，提炼出 EM 算法的符号化表述.

假设给定训练样本 $\{x_1,x_2,\cdots,x_m\}$，我们将隐含类别标签用 $z^{(i)}$ 表示，我们首先认为 $z^{(i)}$ 是满足一定的概率分布的；

这里认为是满足多项式分布:

$$z^{(i)} \approx Multinomial(\phi)$$ 其中 $\phi_j \geq 0,\sum_{j=1}^k \phi_j = 1$，$\phi_j = p(z^{(i)} = j)$ 即第 $i$ 个样本属于第 $j$ 类的概率；$z^{(i)}$ 的可能取值为 $\{1,2,\cdots,k\}$，即共 $k$ 个类别.

假设在 $z^{(i)}$ 确定的条件下，例如 $z^{(i)} = j$，此时 $x^{(i)}$ 也满足一定的概率分布，这里假设是满足多元高斯分布，即:

$$(x^{(i)} | z^{(i)} = j ) \approx \cal{N}(\mu_j,\Sigma_j)$$

我们知道 $x^{(i)}$ 和 $z^{(i)}$ 的联合概率分布为:

$$p(x^{(i)},z^{(i)}) = p(x^{(i)} | z^{(i)}) p(z^{(i)})$$

可以看出模型中有三个参数 $\phi,\mu,\Sigma$，类似高斯判别分析中的处理，我们可以写出似然函数:

$$\begin{array} & l(\phi,\mu,\Sigma) &=& \sum_{i=1}^m \log{p(x^{(i)},z^{(i)};\phi,\mu,\Sigma)} \\&=& \sum_{i=1}^m \log{\sum_{z^{(i)} = 1}^k p(x^{(i)} | z^{(i)};\mu,\Sigma) p(z^{(i)};\phi)} \end{array}$$

然而，这里的 $z^{(i)}$ 为隐含变量，值是不确定的，此时我们就无法通过最大似然概率法则来获得参数值了.

---

在 E 步中，我们是将其他参数 $\phi,\mu,\Sigma$ 看作已知常量，计算当前假设条件下，$x^{(i)}$ 属于每个类别的概率，即:

$$p(z^{(i)} = j | x^{(i)};\phi,\mu,\Sigma) = \frac{p(x^{(i)} | z^{(i)} = j;\mu,\Sigma) p(z^{(i)} = j;\phi)}{\sum_{l=1}^k p(x^{(i)} | z^{(i)} = l;\mu,\Sigma) p(z^{(i)} = l;\phi)}$$

根据初值 $p$，利用贝叶斯公式估计出 $z$（这里估计出的是隐含变量的概率分布的参数）

---

在 M 步中，假如我们知道了类别 $z^{(i)}$ 的值，就可以通过求最大似然概率值获得参数，此时的对数似然目标函数可以简写成:

$$l(\phi,\mu,\Sigma) = \sum_{i=1}^m \log{p(x^{(i)} | z^{(i)};\mu,\Sigma) + \log{p(z^{(i)};\phi)}}$$ 分别将多元高斯分布函数和多项式分布函数展开，令 $l(\phi,\mu,\Sigma)$ 分别对 $\phi,\mu,\Sigma$ 求偏导，并令偏导为零，即可求出参数: $$\begin{array} & \phi_j = \frac{1}{m} \sum_{i=1}^m I(z^{(i)} = j) \\ \mu_j = \frac{\sum_{i=1}^m I(z^{(i)} = j) x^{(i)}}{\sum_{i=1}^m I(z^{(i)} = j)} \\ \Sigma_j = \frac{\sum_{i=1}^m I(z^{(i)} = j) (x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T}{\sum_{i=1}^m I(z^{(i)} = j)} \end{array}$$

利用 E 步估计出的 $z$，反过来用极大似然估计法则估计出 $p$（这里估计出的是概率分布函数的各个参数）

这一步具体求导细节，可参考高斯判别分析一篇.

---

最后总结出基于多项式分布和多元高斯分布的 EM 算法过程如下:

$Repeat \ until \ convergence:\{$
$\qquad (E-step) \quad For \ each \quad i,j \quad in \ set$
$\qquad \qquad w_j^{(i)} = p(z^{(i)} = j | x^{(i)};\phi,\mu,\Sigma)$
$\qquad (M-step) \quad Update \ the \ parameters:$
$\qquad \qquad \phi_j = \frac{1}{m} \sum_{i=1}^m w_j^{(i)}$
$\qquad \qquad \mu_j = \frac{\sum_{i=1}^m w_j^{(i)} x^{(i)}}{\sum_{i=1}^m w_j^{(i)}}$
$\qquad \qquad \Sigma_j = \frac{\sum_{i=1}^m w_j^{(i)} (x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T}{\sum_{i=1}^m w_j^{(i)}}$
$\}$

基本上这个算法过程与第一节中的例子所描述的过程一致；

下面一节会详细的推导出这个算法过程中的每个细节.

---

EM 算法推导

假如我们有训练样本集 $\{x^{(1)},x^{(2)},\cdots,x^{(n)}\}$，我们求模型 $p(x,y)$ 的参数的方法是利用似然值:

$$l(\theta) = \sum_{i=1}^m \log{p(x;\theta)} = \sum_{i=1}^m \log{\sum_{z} p(x,z;\theta)}$$ 但是我们 EM 算法中的目标函数 $l(\phi,\mu,\Sigma)$ 中提到的 $z^{(i)}$ 的值是不确定的随机变量，因此就不能通过上面这中最大似然值的方式求参；但一般确定了 $z$ 后，求解就容易了.

EM 是一种解决存在隐含变量优化问题的有效方法，其思想是: 不断地建立 $l$ 的下界（E 步），然后优化下界（M 步）.

现在看不懂没关系，在下面的推导中会进一步说明.

对于每一个样例 $i$，让 $Q_i$ 表示该样例隐含变量 $z$ 的某种分布（有的书上称作 $Q$ 函数），$Q_i$ 满足 $\sum_{z} Q_i(z) = 1,Q_i(z) \geq 0$（如果 $z$ 是连续性的，那么 $Q_i$ 就是概率密度函数，求和符合就需改成积分符合）.

这样我们可以得到:

$$\begin{array} & l(\theta) &=& \sum_{i} \log{\sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta)} \\&=& \sum_{i} \log{\sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}} \\ &\geq& \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}} \end{array}$$

其中，一式到二式比较直接，就是分子分母同时乘以一个相等的函数；

二式到三式利用了 Jensen不等式；首先 $\log()$ 函数是凹函数，其次根据 lazy Statistician规则，可知 $\sum_{z^{(i)}} Q_i(z^{(i)}) \left[ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \right]$ 其实就是 $\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$ 的数学期望，可以看作 Jensen 不等式中的 $E[f(X)]$，同理，$\sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$ 可以看作 Jensen 不等式中的 $f(E[X])$；根据 Jensen不等式我们可得:

$$f\left( E_{z^{(i)} \approx Q_i} \left[ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \right] \right) \geq E_{z^{(i)}} \left[ f\left( \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \right) \right]$$

Jensen 不等式 和 Lazy Statistician规则 可参考 数学基础篇 中的概率与统计介绍部分.

---

因此，对于任意一种分布 $Q_i$，上面的式子都给 $l(\theta)$ 的值确定了一个下界。但是对于 $Q_i$ 的选择，有多种可能，那种更好呢？

我们知道，在 EM 算法中的 E 步中，$\theta$ 是已知的，即在当前条件下可获得 $\theta$；假设 $\theta$ 已经给定，那么 $l(\theta)$ 的值就决定于 $Q_i(z^{(i)}),p(x^{(i)},z^{(i)})$ 了，于是我们可以调整这两个概率使下界尽可能大（上式 $l(\theta)$ 中的第三式），以逼近 $l(\theta)$ 的真实值，显然当三式等于二式时，$l(\theta)$ 的下限最大，而根据 Jensen不等式我们可知当且仅当 $X$ 是常量时等号成立，这里的 $\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$ 就是 Jensen不等式中的 $X$，我们假设 $\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = c \Rightarrow Q_i(z^{(i)}) = \frac{p(x^{(i)},z^{(i)};\theta)}{c}$，其中 $c$ 是一个不依赖于 $z^{(i)}$ 的常数；

我们知道 $\sum_{z} Q_i(z^{(i)}) = 1$，因此可得:

$$\sum_{z} p(x^{(i)},z^{(i)};\theta) = \sum_{z} c Q_i(z^{(i)}) = c$$ 进而可得: $$\begin{array} & Q_i(z^{(i)}) &=& \frac{p(x^{(i)},z^{(i)};\theta)}{c} = \frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z} p(x^{(i)},z^{(i)};\theta)} \\&=& \frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} \\&=& p(z^{(i)} | x^{(i)};\theta) \end{array}$$
其中最后一步用到了条件概率公式.

现在我们知道 $Q_i(z^{(i)})$ 该如何选择了，这一步就是 E 步，建立 $l(\theta)$ 的下界；

接下来就是 M 步，在给定 $Q_i(z^{(i)})$ 后，调整 $\theta$，去极大化 $l(\theta)$ 的下界（在固定 $Q_i(z^{(i)})$ 后，下界还可以调整的更大）；这一步求解就是根据具体的 $x^{(i)},z^{(i)}$ 的联合概率分布使用拉格朗日乘子法来对 $l(\theta)$ 求极值，如上一节所述.

---

于是一般的 EM 算法的步骤如下:

$Repeat \ until \ convergence \ \{$
$\qquad (E-step) \ For \ each \quad i \quad set$
$\qquad \qquad Q_i(z^{(i)}) := p(z^{(i)} | x^{(i)};\theta)$
$\qquad (M-step) \ Set$
$\qquad \qquad \theta := arg \max_{\theta} \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$
$\}$

若这里的 $Q_i(z^{(i)})$ 为多项式概率分布，$p(x^{(i)},z^{(i)};\theta)$ 为多元高斯分布，则 EM 算法过程就为上一节最后的描述.

---

下面我们来证明 EM 算法的收敛性:

假设 $\theta^{(t)},\theta^{(t+1)}$ 分别为第 $t$ 次和 $t+1$ 次迭代后的结果，如果我们证明 $l(\theta^{(t)}) \leq l(\theta^{(t+1)})$ ，也就是说极大似然估计函数单调增加，那么最终我们会到达最大似然估计的最大值。

下面来证明，选定 $\theta^{(t)}$ 后，我们得到 E 步，为了能取Jensen不等式的等号，选取 $Q_i(z^{(i)})$ 如下:

$$Q_i^{(t)}(z^{(i)}) := p(z^{(i)} | x^{(i)};\theta^{(t)})$$ 进而等号满足: $$l(\theta^{(t)}) = \sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}}$$

然后我们通过最大化上面等式的右边获得了新的参数 $\theta^{(t+1)}$ .此时必然有:

$$\begin{array} & l(\theta^{(t+1)}) &\geq& \sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})}} \\&\geq& \sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}} \\&=& l(\theta^{(t)}) \end{array}$$

上面第一式是基于 $l(\theta)$ 的下界得到，即

$$l(\theta) \geq \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$$

上面第二式是利用的 M 步的定义，因为 M 步就是将 $\theta^{(t)}$ 调整到 $\theta^{(t+1)}$ 使得

$$\theta := arg \max_{\theta} \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$$

这样就证明了 $l(\theta)$ 是单调增加的，因此 EM 算法是收敛的。

---

如果我们定义:

$$J(Q,\theta) = \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log{\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$$ 从前面的推导中我们知道 $l(\theta) \geq J(Q,\theta)$，EM 可以看作是 $J$ 的坐标上升法，E 步固定 $\theta$，优化 $Q$，M 步固定 $Q$ 优化 $\theta$ .

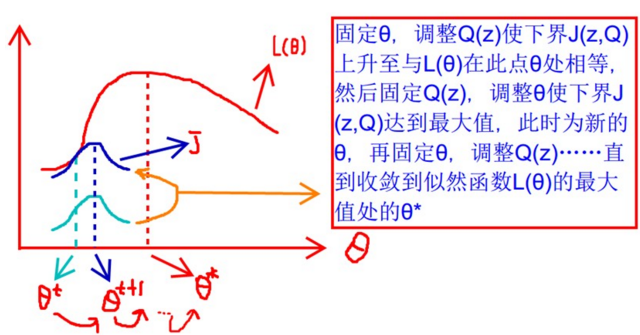
下面这张图很好的说明了 EM算法的优化过程:

---

R 程序演示

一般我们用 EM 算法做聚类比较多，R 中专门提供了一个 mclust包，利用混合高斯模型对数据进行聚类分析，下面我们利用 iris 数据集进行演示:

首先安装 mclust包:

> install.packages("mclust")
# 加载包
> library(mclust)

利用包中的 Mclust()函数进行聚类:

# 混合高斯模型聚类
> mc <- Mclust(iris[,1:4], 3)
fitting ...
  |=================================================================================| 100%
# 查看聚类结果对象的结构
> summary(mc)
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm 
----------------------------------------------------
Mclust VEV (ellipsoidal, equal shape) model with 3 components:
 log.likelihood   n df       BIC       ICL
       -186.074 150 38 -562.5522 -566.4673
Clustering table:
 1  2  3 
50 45 55 
# 可视化聚类结果
> plot(mc,  what=c('classification'),dimens=c(3,4))
# 输出混淆矩阵，查看聚类精度
> table(iris$Species, mc$classification)
              1  2  3
  setosa     50  0  0
  versicolor  0 45  5
  virginica   0  0 50
> 

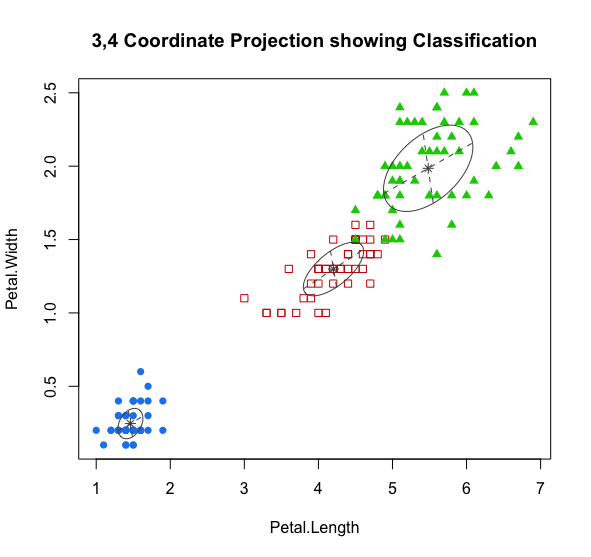
其中，Mclust()方法的原型为 Mclust(data, G = NULL, modelNames = NULL, prior = NULL, control = emControl(), initialization = NULL, warn = mclust.options("warn"), x = NULL, verbose = interactive(), ...)

data 参数为原数据集；
G 为预设类别数，默认值为 1 至 9，即由软件根据 BIC 的值在 1 至 9 中选择最优值.

其他参数可参看 help("Mclust") 进行查看.

summary(mc) 的输出结果显示聚了三类，标出了每类的数量；如果想看更详细的输出参数，可以使用 summary(mc,parameters = TRUE)；

plot() 函数的参数可以参照 help("plot.Mclust") 进行查看.

---

若参数 data 所指的数据集有两个属性，则可以绘出密度图:

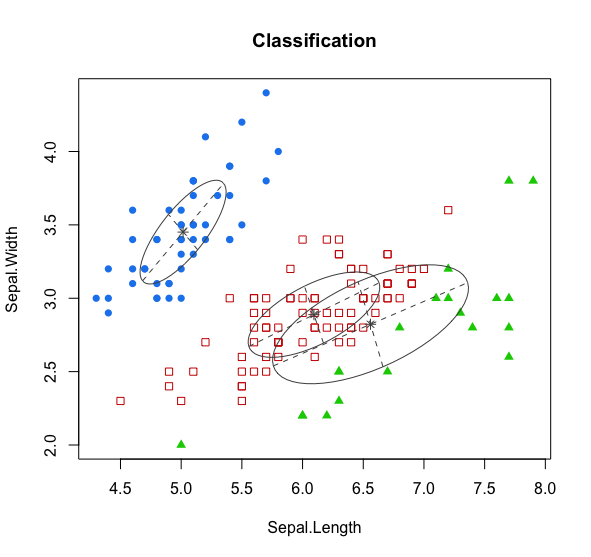
# 数据集只有两个属性时
> mc <- Mclust(iris[,1:2],3)
fitting ...
  |=====================================================================| 100%
# 绘制聚类结果图
> mclust2Dplot(iris[,1:2],parameters = mc$parameters,z = mc$z,what = "classification",main = TRUE)

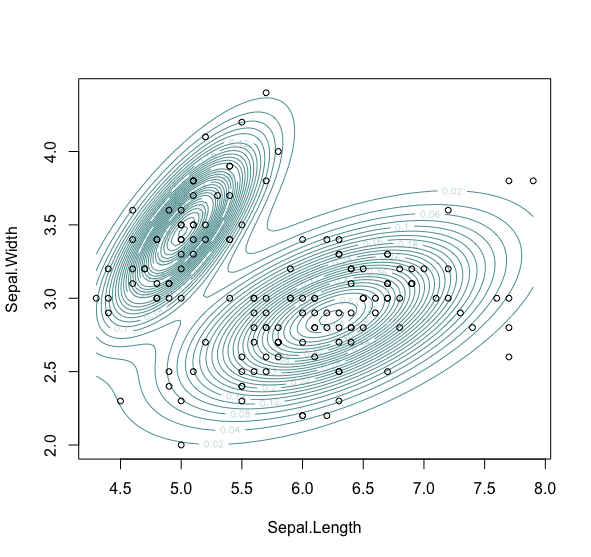
# 生成聚类密度对象
> model_density <- densityMclust(iris[,1:2])
fitting ...
  |=====================================================================| 100%
# 绘制高斯混合模型的二维密度图
> plot(model_density,iris[,1:2],col = "cadetblue",nlevels = 25,what = "density")

# 绘制高斯混合模型的三维密度图
> plot(model_density,what = "density",type = "persp",theta = 235)
>

若想自己实现 EM 算法，可参看 http://www.jianshu.com/p/8acf6ec8193e

---

参考

• http://www.jianshu.com/p/1121509ac1dc
• http://blog.csdn.net/yzheately/article/details/51068855
• http://blog.csdn.net/yzheately/article/details/51150752
• http://blog.csdn.net/yzheately/article/details/51164441
• http://blog.csdn.net/baimafujinji/article/details/50626149