机器学习篇

牛顿法与拟牛顿法

笔者在整理 CRF 算法的时候，对最后一步学习过程没大看懂，于是专门找时间调研了下拟牛顿法。

本篇基本上转载至 : http://blog.csdn.net/itplus/article/details/21896453
因为这是笔者看过的将拟牛顿法讲的最清楚的一篇。

最后笔者再结合 java 代码去分析 LBFSG 算法的实现过程。

---

考虑如下无约束的极小化问题:

$$\min_{x} f(\boldsymbol{x})$$ 其中 $\boldsymbol{x} = (x_1,x_2,\cdots,x_N)^T \in R^N$.

本文不讨论收敛性问题，因此不妨对目标函数 $f: R^N \rightarrow R$ 作一个较苛刻的假设，我们假设 $f$ 为凸函数，且两阶连续可微。令极小问题的解为 $\boldsymbol{x}^*$

梯度下降法

梯度下降法又被称为最速下降法（Steepest descend method），其理论基础是梯度的概念。

梯度与方向导数的关系：梯度的方向与取得最大方向导数值的方向一致，而梯度的模就是函数在该点的方向导数的最大值。

对于一个无约束的优化问题：

$$\min_{x} f(x)$$

梯度下降的更新公式为:

$$x_{k+1} = x_k - \alpha \frac{d y}{d x}|_{x = x_k}$$ 其中，$\alpha$ 为步长因子，可以取固定常数，如 $\alpha = 0.5$；梯度方向为 $\frac{d y}{d x}|_{x = x_k}$

例如: $f(x) = x^2$

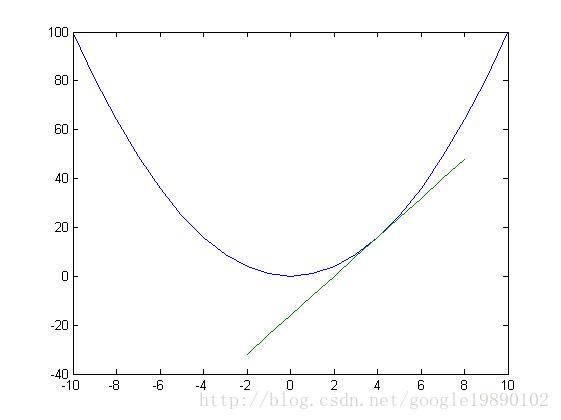
如图，在 $x = 4$ 处的切线。显然在 $x = 0$ 处函数取得最小值。沿着梯度的方向是下降速度最快的方向。

具体的过程为：初始时，任取 $x$ 的值，如取 $x = 4$，则对应的 $y = 16$。利用梯度下降法 $x_1 = x_0 - \alpha \frac{d y}{d x}|_{x = x_k}$，去更新 $x$。不断迭代，算法终止的判断标准是：$|y_1 - y_2| \leq \epsilon$，其中 $\epsilon$ 是一个指定的阈值。

---

梯度下降的算法流程为：

1. 初始化：随机选取取值范围内的任意数

2. 迭代操作：
   计算梯度 $\frac{d y}{d x}|_{x = x_k}$；
   修改新的变量 $x_{k+1} = x_k - \alpha \frac{d y}{d x}|_{x = x_k}$；
   判断是否达到终止: 如果 $|y_1 - y_2| \leq \epsilon$，则跳出循环；否则继续；

3. 输出终止结果

牛顿法

为了由浅入深的讨论，我们考虑 $N = 1$ 的简单情形（此时目标函数 $f(\boldsymbol{x})$ 变为 $f(x)$）.牛顿法的基本思想是：在现有极小点估计值的附近对 $f(x)$ 做二阶泰勒展开，进而找到极小点的下一个估计值。

设 $x_k$ 为当前的极小点估计值，则:

$$\varphi(x) = f(x_k) + f'(x_k)(x - x_k) + \frac{1}{2} f''(x_k)(x-x_k)^2$$
表示 $f(x)$ 在 $x_k$ 附近的二阶泰勒展开式（其中略去了关于 $x - x_k$ 的高阶无穷小项）。

由于求的是最值，由极值必要条件可知，$\varphi(x)$ 应满足：

$$\varphi'(x) = 0$$

即：

$$f'(x_k) + f''(x_k)(x-x_k) = 0$$

解得：

$$x = x_k - \frac{f'(x_k)}{f''(x_k)}$$

于是，若给定初始值 $x_0$，则可以构造如下的迭代格式:

$$x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)},k = 0,1,\cdots$$ 产生序列 $\{x_k\}$ 来逼近 $f(x)$ 的极小点。在一定条件下，$\{x_k\}$ 可以收敛到 $f(x)$ 的极小点。

---

对于 $N > 1$ 的情形，二阶泰勒展开式可以做推广，此时:

$$\varphi(\boldsymbol{x}) = f(\boldsymbol{x}_k) + \nabla f(\boldsymbol{x}_k) (\boldsymbol{x} - \boldsymbol{x}_k) + \frac{1}{2} (\boldsymbol{x} - \boldsymbol{x}_k)^T \nabla^2 f(\boldsymbol{x}) (\boldsymbol{x} - \boldsymbol{x}_k)$$

其中 $\nabla f$ 为 $f$ 的梯度向量，$\nabla^2 f$ 为 $f$ 的海森矩阵（Hessian matrix），其定义分别为:

$$\begin{array} & \nabla f &=& \left[ \begin{matrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_N} \\ \end{matrix} \right] \\ \nabla^2 f &=& \left[ \begin{matrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_N} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_N} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_N \partial x_1} & \frac{\partial^2 f}{\partial x_N \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_N^2} \\ \end{matrix} \right]_{N \times N} \end{array}$$

注意：$\nabla f$ 和 $\nabla^2 f$ 中的元素均为关于 $\boldsymbol{x}$ 的函数，以下分别将其简记为 $g,H$ .

特别的，若 $f$ 的混合偏导数可交换次序，即对 $\forall i,j$，成立 $\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}$，则海森矩阵 $H$ 为对称矩阵.

而 $\nabla f(\boldsymbol{x}_k), \nabla^2 f(\boldsymbol{x}_k)$ 则表示将 $\boldsymbol{x}$ 取为 $\boldsymbol{x}_k$ 后得到的实值向量和矩阵，以下分别将其简记为 $g_k,H_k$（这里字母 g 表示 gradient，H 表示 Hessian）

同样地，由于是求极小点，极值必要条件要求它为 $\varphi(\boldsymbol{x})$ 的驻点，即:

$$\nabla \varphi(\boldsymbol{x}) = 0$$

驻点: http://www.baike.com/wiki/%E9%A9%BB%E7%82%B9

对泰勒展开使用梯度算子得:

$$g_k + H_k (\boldsymbol{x} - \boldsymbol{x}_k) = 0$$

梯度算子: http://www.docin.com/p-79757964.html

泰勒展开式的第二项应用梯度算子得到的是 $(\boldsymbol{x} - \boldsymbol{x}_k)$ 的高阶无穷小，所以省略.

进一步，若矩阵 $H_k$ 非奇异，则可解得:

$$\boldsymbol{x} = \boldsymbol{x}_k - H_k^{-1} g_k$$

于是，若给定初始值 $\boldsymbol{x}_0$，则同样可以构造出迭代格式:

$$\boldsymbol{x}_{k+1} = \boldsymbol{x}_k - H_k^{-1} g_k, k = 0,1,\cdots$$

这就是原始的牛顿迭代法，其迭代格式中的搜索方向 $d_k = -H_k^{-1} g_k$ 称为牛顿方向.

矩阵非奇异: https://www.zhihu.com/question/35318893
https://baike.baidu.com/item/%E9%9D%9E%E5%A5%87%E5%BC%82%E7%9F%A9%E9%98%B5/4114613?fr=aladdin

下面给出完整的牛顿法的算法描述:

1. 给定初值 $\boldsymbol{x}_0$ 和精度阈值 $\epsilon$，并令 $k := 0$

2. 计算 $g_k,H_k$

3. 若 $||g_k|| < \epsilon$，则停止迭代；否则确定搜索方向 $d_k = -H_k^{-1} g_k$.

4. 计算新的迭代点 $\boldsymbol{x}_{k+1} := \boldsymbol{x}_{k} + d_k$

5. 令 $k := k+1$，转至第2步.

当目标函数是二次函数时，由于二次泰勒展开函数与原目标函数不是近似而是完全相同的二次式，海森矩阵退化成一个常数矩阵，从任一初始点出发，利用 $\boldsymbol{x}_{k+1}$ 的迭代式，只需一步迭代即可达到 $\boldsymbol{x}$ 的极小点 $\boldsymbol{x}^*$ ，因此牛顿法是一种具有二次收敛性的算法。对于非二次函数，若函数的二次性态较强，或迭代点已进入极小点的领域，则其收敛速度也是很快的，这是牛顿法的主要优点.

但原始牛顿法由于迭代公式中没有步长因子，而是定步长迭代，对于非二次目标函数来说，有时会使函数值上升，即出现 $f(\boldsymbol{x}_{k+1}) > f(\boldsymbol{x}_k)$ 的情况，这表明原始牛顿法不能保证函数值稳定地下降.在严重的情况下甚至可能造成迭代点列 $\{\boldsymbol{x}_k\}$ 的发散而导致计算失败.

---

为了消除原始牛顿迭代法的弊病，人们提出“阻尼牛顿法”，阻尼牛顿法每次迭代的方向仍采用 $d_k$，但每次迭代需沿此方向作一维搜索（line search），寻求最优的步长因子 $\lambda_k$，即:

$$\lambda_k = arg \min_{\lambda \in R} f(\boldsymbol{x}_k + \lambda d_k)$$

阻尼牛顿法的算法过程，就是将上步原始牛顿法中的迭代公式增加步长，改成 $\boldsymbol{x}_{k+1} := \boldsymbol{x}_{k} + \lambda d_k$

---

拟牛顿条件

牛顿法虽然收敛速度快（因为不仅考虑了梯度，而且考虑了梯度的加速方向），但是计算过程中需要计算目标函数的二阶偏导数，计算复杂度较大.而且有时目标函数的海森矩阵无法保持正定，从而使得牛顿法失效.为了克服这两个问题，人们提出了拟牛顿法.

基本思想是：不用二阶偏导数，而是构造出可以近似海森矩阵（或海森矩阵的逆）的正定对称矩阵，在“拟牛顿”的条件下优化目标函数.

拟牛顿条件，或者叫做拟牛顿方程、割线条件.

因为对海森矩阵的近似需要理论指导，该近似矩阵需要满足一定的条件.

一致定义如下：用 $B$ 表示对海森矩阵 $H$ 本身的近似，而用 $D$ 表示对海森矩阵的逆 $H^{-1}$ 的近似，即 $B \approx H,D \approx H^{-1}$ .

设经过 $k+1$ 次迭代后得到 $\boldsymbol{x}_{k+1}$，此时将目标函数

$$f(\boldsymbol{x}) \approx f(\boldsymbol{x}_{k+1}) + \nabla f(\boldsymbol{x}_{k+1}) (\boldsymbol{x} - \boldsymbol{x}_{k+1}) + \frac{1}{2} (\boldsymbol{x} - \boldsymbol{x}_{k+1})^T \nabla^2 f(\boldsymbol{x}_{k+1}) (\boldsymbol{x} - \boldsymbol{x}_{k+1})$$

在上式两边同时作用一个梯度算子 $\nabla$，可得：

$$\nabla f(\boldsymbol{x}) \approx \nabla f(\boldsymbol{x}_{k+1}) + H_{k+1} (\boldsymbol{x} - \boldsymbol{x}_{k+1})$$

当 $\boldsymbol{x} = \boldsymbol{x}_k$ 时有:

$$g_k \approx g_{k+1} + H_{k+1} (\boldsymbol{x}_k - \boldsymbol{x}_{k+1}) \\ g_{k+1} - g_k \approx H_{k+1} (\boldsymbol{x}_{k+1} - \boldsymbol{x}_k)$$

若引入记号：

$$s_k = \boldsymbol{x}_{k+1} - \boldsymbol{x}_k \\ y_k = g_{k+1} - g_k$$

则可整理得:

$$y_k \approx H_{k+1} s_k$$
或者: $$s_k \approx H_{k+1}^{-1} y_k$$

这就是所谓的拟牛顿条件，它对迭代过程中的海森矩阵 $H_{k+1}$ 作约束，因此，对 $H_{k+1}$ 做近似的 $B_{k+1}$ ，以及对 $H_{k+1}^{-1}$ 做近似的 $D_{k+1}$ 可以将 :

$$y_k = B_{k+1} s_k \\ s_k = D_{k+1} y_k$$
作为指导.

下面一节讨论几种具体的拟牛顿算法，即讨论如何去近似海森矩阵或其逆矩阵.

---

DFP算法

DFP 算法是以 William C.Davidon、Roger Fletcher、Michael J.D.Powell 三个人的名字的首字母命名的，它由 Davidon 于 1959 年首先提出，后经 Fletcher 和 Powell 加以发展和完善，是最早的拟牛顿法.

该算法的核心是：通过迭代的方法，对 $H_{k+1}^{-1}$ 做近似。迭代格式为

$$D_{k+1} = D_k + \Delta D_k,k = 0,1,2,\cdots$$
其中的 $D_0$ 通常取为单位矩阵 $I$. 因此，关键是每一步的矫正矩阵 $\Delta D_k$ 如何构造.

关于 $\Delta D_k$ 的构造，是真的有点 tricky，使用的是“待定法”，即首先将 $\Delta D_k$ 待定成某种形式，然后结合拟牛顿条件来进行推导：

$$\Delta D_k = \alpha \boldsymbol{\mu} \boldsymbol{\mu}^T + \beta \boldsymbol{v} \boldsymbol{v}^T$$

其中，$\alpha,\beta$ 为待定系数，$\boldsymbol{\mu},\boldsymbol{v} \in R^N$ 为待定向量. 从形式上看，这种待定公式至少保证了矩阵 $\Delta D_k$ 的对称性（因为 $\boldsymbol{\mu} \boldsymbol{\mu}^T,\boldsymbol{v} \boldsymbol{v}^T$ 均为对称矩阵）.

$$\begin{array} & \because s_k &=& D_{k+1} y_k \\ D_{k+1} &=& D_k + \Delta D_k \\ \therefore s_k &=& D_k y_k + \alpha \boldsymbol{\mu} \boldsymbol{\mu}^T y_k + \beta \boldsymbol{v} \boldsymbol{v}^T y_k \end{array}$$

下面一步的构造就特别精彩：

$$\begin{array} & s_k &=& D_k y_k + \boldsymbol{\mu} (\alpha \boldsymbol{\mu}^T y_k) + \boldsymbol{v} (\beta \boldsymbol{v}^T y_k) \\ &=& D_k y_k + (\alpha \boldsymbol{\mu}^T y_k) \boldsymbol{\mu} + (\beta \boldsymbol{v}^T y_k) \boldsymbol{v} \end{array}$$

看到了吧，括号中的 $(\alpha \boldsymbol{\mu}^T y_k),(\beta \boldsymbol{v}^T y_k)$ 是两个数，既然是数，我们不妨作如下简单赋值:

$$\alpha \boldsymbol{\mu}^T y_k = 1 \\ \beta \boldsymbol{v}^T y_k = -1$$

即:

$$\alpha = \frac{1}{\boldsymbol{\mu}^T y_k} \\ \beta = -\frac{1}{\boldsymbol{v}^T y_k}$$
其中向量 $\boldsymbol{\mu},\boldsymbol{v}$ 仍有待确定.

其中，$\boldsymbol{\mu},\boldsymbol{v},y_k$ 都是 $n \times 1$ 的向量，所以 $\alpha \boldsymbol{\mu}^T y_k,\beta \boldsymbol{v}^T y_k$ 都是一个数.

那么 $\boldsymbol{\mu},\boldsymbol{v}$ 如何确定呢？将上面的 $\alpha,\beta$ 带入 $s_k$，得:

$$\boldsymbol{\mu} - \boldsymbol{v} = s_k - D_k y_k$$ 要上式成立，不妨直接设: $$\begin{array} & \boldsymbol{\mu} &=& s_k \\ \boldsymbol{v} &=& D_k y_k \end{array}$$ 于是，$\alpha,\beta$ 最终的表达式为: $$\begin{array} & \alpha &=& \frac{1}{s_k^T y_k} \\ \beta &=& -\frac{1}{(D_k y_k)^T y_k} = -\frac{1}{y_k^T D_k y_k} \end{array}$$
其中第二个等式用到了 $D_k$ 的对称性.

至此，我们就将矫正矩阵 $\Delta D_k$ 构造出来了:

$$\Delta D_k = \frac{s_k s_k^T}{s_k^T y_k} - \frac{D_k y_k y_k^T D_k}{y_k^T D_k y_k}$$

---

综上，我们给出 DFP 算法的完整描述:

1. 给定初值 $\boldsymbol{x}_0$ 和精度阈值 $\epsilon$，并令 $D_0 = I, k:= 0$

2. 确定搜索方向 $d_k = -D_k g_k$

3. 利用阻尼牛顿法中的 $\lambda_k$ 表达式，得到步长 $\lambda_k$，令 $s_k = \lambda_k d_k,\boldsymbol{x}_{k+1} := \boldsymbol{x}_k + s_k$

4. 若 $||g_{k+1}|| < \epsilon$，则算法结束.

5. 计算 $y_k = g_{k+1} -g_k$

6. 计算 $D_{k+1} = D_k + \frac{s_k s_k^T}{s_k^T y_k} - \frac{D_k y_k y_k^T D_k}{y_k^T D_k y_k}$

7. 令 $k := k+1$，转至第 2 步.

---

BFGS

BFGS 算法是以其发明者 Broyden,Fletcher,Goldfarb 和 Shanno 四人的名字首字母命名的。

与 DFP 算法相比，BFGS 算法性能更佳，目前它已成为求解无约束非线性优化问题最常用的方法之一.

BFGS 算法中核心公式的推导过程和 DFP 完全类似，只是 BFGS 是去逼近海森矩阵，而不是像 DFP 去逼近海森矩阵的逆.

即 $B_k \approx H_k$，设迭代格式为:

$$B_{k+1} = B_k + \Delta B_k,k = 0,1,2,\cdots$$ 其中的 $B_0$ 也常取为单位矩阵 $I$.

这里的问题同样是如何构造矫正矩阵 $\Delta B_k$，同样将其待定为:

$$\Delta B_k = \alpha \boldsymbol{\mu} \boldsymbol{\mu}^T + \beta \boldsymbol{v} \boldsymbol{v}^T$$ 利用拟牛顿条件得: $$y_k = B_k s_k + (\alpha \boldsymbol{\mu}^T s_k)\boldsymbol{\mu} + (\beta \boldsymbol{v}^T s_k) \boldsymbol{v}$$

通过令 $\alpha \boldsymbol{\mu}^T s_k = 1,\beta \boldsymbol{v}^T s_k = -1$，以及

$$\boldsymbol{\mu} = y_k, \boldsymbol{v} = B_k s_k$$

可算得：

$$\alpha = \frac{1}{y_k^T s_k}, \beta = -\frac{1}{s_k^T B_k s_k}$$
综上，便可得到矫正矩阵 $\Delta B_k$ 的公式: $$\Delta B_k = \frac{y_k y_k^T}{y_k^T s_k} - \frac{B_k s_k s_k^T B_k}{s_k^T B_k s_k}$$

---

最后同样给出完整的 BFGS 算法的描述:

1. 给定初值 $\boldsymbol{x}_0$ 和精度阈值 $\epsilon$，并令 $B_0 = I, k:= 0$

2. 确定搜索方向 $d_k = -B_k^{-1} g_k$

3. 利用阻尼牛顿法中的 $\lambda_k$ 表达式，得到步长 $\lambda_k$，令 $s_k = \lambda_k d_k,\boldsymbol{x}_{k+1} := \boldsymbol{x}_k + s_k$

4. 若 $||g_{k+1}|| < \epsilon$，则算法结束.

5. 计算 $y_k = g_{k+1} -g_k$

6. 计算 $B_{k+1} = B_k + \frac{y_k y_k^T}{y_k^T s_k} - \frac{B_k s_k s_k^T B_k}{s_k^T B_k s_k}$

7. 令 $k := k+1$，转至第 2 步.

其中算法的第 2 步，通常是通过求解线性代数方程组 $B_k d_k = -g_k$ 来进行的。然而，更一般的做法是：通过对步 6 中的递推关系应用 Sherman-Morrison公式，直接给出 $B_{k+1}^{-1}$ 与 $B_k^{-1}$ 之间的关系式:

$$B_{k+1}^{-1} = \left( I - \frac{s_k y_k^T}{y_k^T s_k} \right) B_k^{-1} \left( I - \frac{y_k s_k^T}{y_k^T s_k} \right) + \frac{s_k s_k^T}{y_k^T s_k}$$

这里笔者还没看懂怎么得出来的.

关于 Sherman-Morrison 公式:

设 $A \in R^n$ 为非奇异方阵，$\boldsymbol{\mu},\boldsymbol{v} \in R^n$，若 $1 + \boldsymbol{v}^T A^{-1} \boldsymbol{\mu} \neq 0$

$$(A + \boldsymbol{\mu} \boldsymbol{v}^T)^{-1} = A^{-1} - \frac{A^{-1} \boldsymbol{\mu} \boldsymbol{v}^T A^{-1}}{1 + \boldsymbol{v}^T A^{-1} \boldsymbol{\mu}}$$

于是，上述 BFGS 算法的描述可以改写如下. 注意，为了避免出现矩阵求逆符号，统一将 $B_i^{-1}$ 换用成 $D_i$ （这样仅仅是为了看上去舒服）.

1. 给定初值 $\boldsymbol{x}_0$ 和精度阈值 $\epsilon$，并令 $D_0 = I, k:= 0$

2. 确定搜索方向 $d_k = -D_k g_k$

3. 利用阻尼牛顿法中的 $\lambda_k$ 表达式，得到步长 $\lambda_k$，令 $s_k = \lambda_k d_k,\boldsymbol{x}_{k+1} := \boldsymbol{x}_k + s_k$

4. 若 $||g_{k+1}|| < \epsilon$，则算法结束.

5. 计算 $y_k = g_{k+1} -g_k$

6. 计算 $D_{k+1} = \left( I - \frac{s_k y_k^T}{y_k^T s_k} \right) D_k^{-1} \left( I - \frac{y_k s_k^T}{y_k^T s_k} \right) + \frac{s_k s_k^T}{y_k^T s_k}$

7. 令 $k := k+1$，转至第 2 步.

对比下 BFGS 和 DFP 算法，唯一不同的仅在于 $D_{k+1}$ 的迭代公式不同罢了.

---

LBFGS

在 BFGS 算法中，需要用到一个 $N \times N$ 的矩阵 $D_k$，当 $N$ 很大时，存储这个矩阵将变得很耗计算机资源.例如考虑 $N$ 为 10 万 的情形，且用 double 型（8 字节）来存储 $D_k$，需要多大的内存呢？我们来计算一下:

$$\frac{N 阶矩阵的字节数}{1 GB 的字节数} = \frac{10^5 \times 10^5 \times 8}{2^{10} \times 2^{10} \times 2^{10}} = 74.5(GB)$$
74.5 GB，很惊人是吧，这对于一般的服务器是很难承受的。当然，考虑到矩阵 $D_k$ 的对称性，内存还可以降一半，但是，在机器学习问题中，像 10 万这样的规模还只能算是中小规模。那么，是否可以通过对 BFGS 算法进行改造，从而减少其迭代过程中所需的内存开销呢？

答案是肯定的，L-BFGS(Limited-memory BFGS 或 Limited-storage BFGS) 算法就是这样一种算法.它对 BFGS 算法进行了近似，其基本思想是：不再存储完整的矩阵 $D_k$，而是存储计算过程中的向量序列 $\{s_i\},\{y_i\}$，需要矩阵 $D_k$ 时，利用向量序列 $\{s_i\},\{y_i\}$ 的计算来代替.而且，向量序列 $\{s_i\},\{y_i\}$ 也不是所有的都存，而是固定存最新的 $m$ 个（参数 $m$ 可由用户根据自己机器的内存自行指定）.每次计算 $D_k$ 时，只利用最新的 $m$ 个 $\{s_i\},\{y_i\}$. 显然，这样做就将存储由原来的 $O(N^2)$ 降到了 $O(mN)$.

接下来，讨论 L-BFGS 算法的具体实现过程.我们的出发点是修改如下迭代式:

$$D_{k+1} = \left( I - \frac{s_k y_k^T}{y_k^T s_k} \right) D_k \left( I - \frac{y_k s_k^T}{y_k^T s_k} \right) + \frac{s_k s_k^T}{y_k^T s_k}$$ 若记 $\rho_k = \frac{1}{y_k^T s_k},V_k = I - \rho_k y_k s_k^T$，则上式可写成: $$D_{k+1} = V_k^T D_k V_k + \rho_k s_k s_k^T$$
如果给定初始矩阵 $D_0$ （通常为正定的对角矩阵，如 $D_0 = I$），则依次可得: $$\begin{array} & D_1 &=& V_0^T D_0 V_0 + \rho_0 s_0 s_0^T \\ D_2 &=& V_1^T D_1 V_1 + \rho_1 s_1 s_1^T \\ &=& V_1^T (V_0^T D_0 V_0 + \rho_0 s_0 s_0^T) V_1 + \rho_1 s_1 s_1^T \\ &=& V_1^T V_0^T D_0 V_0 V_1 + V_1^T \rho_0 s_0 s_0^T V_1 + \rho_1 s_1 s_1^T \\ D_3 &=& V_2^T D_2 V_2 + \rho_2 s_2 s_2^T \\ &=& V_2^T (V_1^T V_0^T D_0 V_0 V_1 + V_1^T \rho_0 s_0 s_0^T V_1 + \rho_1 s_1 s_1^T) V_2 + \rho_2 s_2 s_2^T \\ &=& V_2^T V_1^T V_0^T D_0 V_0 V_1 V_2 + V_2^T V_1^T \rho_0 s_0 s_0^T V_1 V_2 + V_2^T \rho_1 s_1 s_1^T V_2 + \rho_2 s_2 s_2^T \\ \cdots \end{array}$$

一般地，我们有:

$$\begin{array} & D_{k+1} &=& (V_k^T V_{k-1}^T \cdots V_1^T V_0^T) D_0 (V_0 V_1 \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_2^T V_1^T)(\rho_0 s_0 s_0^T)(V_1 V_2 \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_3^T V_2^T)(\rho_1 s_1 s_1^T)(V_2 V_3 \cdots V_{k-1} V_k) \\&+& \cdots \\ &+& (V_k^T V_{k-1}^T)(\rho_{k-2} s_{k-2} s_{k-2}^T) (V_{k-1} V_{k}) \\&+& V_k^T (\rho_{k-1} s_{k-1} s_{k-1}^T) V_k \\ &+& \rho_k s_k s_k^T \end{array}$$

由上式可见，计算 $D_{k+1}$ 需用到 $\{s_i,y_i\}_{i=0}^k$，因此，若从 $s_0,y_0$ 开始连续地存储 $m$ 组的话，只能存储到 $s_{m-1},y_{m-1}$ ，亦即，只能依次计算 $D_1,D_2,\cdots$ 直到 $D_m$. 那么，$D_{m+1},D_{m+2}$ 该如何计算呢？

自然地，如果一定要丢掉一些向量，那么肯定优先考虑那些最早生成的向量. 具体来说，计算 $D_{m+1}$ 时，我们保存 $\{s_i,y_i\}_{i=1}^m$，丢掉了 $\{s_0,y_0\}$；计算 $D_{m+2}$ 时，我们保存 $\{s_i,y_i\}_{i=2}^{m+1}$，丢掉了 $\{s_i,y_i\}_{i=2}^1;\cdots$

但是舍弃掉一些向量后，就只能 近似计算 了，当 $k+1 > m$ 时，可以构造近似计算公式:

$$\begin{array} & D_{k+1} &=& (V_k^T V_{k-1}^T \cdots V_{k-m+2}^T V_{k-m+1}^T) D_0 (V_{k-m+1} V_{k-m+2} \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_{k-m+3}^T V_{k-m+2}^T)(\rho_0 s_0 s_0^T)(V_{k-m+2} V_{k-m+3} \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_{k-m+4}^T V_{k-m+3}^T)(\rho_1 s_1 s_1^T)(V_{k-m+3} V_{k-m+4} \cdots V_{k-1} V_k) \\&+& \cdots \\ &+& (V_k^T V_{k-1}^T)(\rho_{k-2} s_{k-2} s_{k-2}^T) (V_{k-1} V_{k}) \\&+& V_k^T (\rho_{k-1} s_{k-1} s_{k-1}^T) V_k \\ &+& \rho_k s_k s_k^T \end{array}$$

这被称为 special BFGS matrices. 若引入 $\hat{m} = \min\{k,m-1\}$，则还可以推出：

$$\begin{array} & D_{k+1} &=& (V_k^T V_{k-1}^T \cdots V_{k-m+1}^T V_{k-m}^T) D_0 (V_{k-m} V_{k-m+1} \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_{k-m+2}^T V_{k-m+1}^T)(\rho_0 s_0 s_0^T)(V_{k-m+1} V_{k-m+2} \cdots V_{k-1} V_k) \\&+& (V_k^T V_{k-1}^T \cdots V_{k-m+3}^T V_{k-m+2}^T)(\rho_1 s_1 s_1^T)(V_{k-m+2} V_{k-m+3} \cdots V_{k-1} V_k) \\&+& \cdots \\ &+& (V_k^T V_{k-1}^T)(\rho_{k-2} s_{k-2} s_{k-2}^T) (V_{k-1} V_{k}) \\&+& V_k^T (\rho_{k-1} s_{k-1} s_{k-1}^T) V_k \\ &+& \rho_k s_k s_k^T \end{array}$$

看到这里，读者千万不要被上面冗长复杂的形式所吓到。事实上，由 BFGS 算法流程易知，$D_k$ 的作用仅用来计算 $D_k g_k$ 获取搜索方向，因此，若能利用上述表达式设计出一种计算 $D_k g_k$ 的快速算法，则大功告成：

算法：（$D_k g_k$ 的快速算法）

Step 1 初始化:

$$\begin{array} & \delta = \begin{cases} 0, & 若 k \leq m \\ k-m, & 若 k > m \end{cases} \\ L = \begin{cases} k, & 若 k \leq m \\ m, & 若 k > m \end{cases} \\ \boldsymbol{q}_L = g_k \end{array}$$

Step 2 后向循环:
$\qquad FOR \quad i = L-1,L-2,\cdots,1,0 \quad DO$
$\qquad \{$
$\qquad \qquad j = i + \delta;$
$\qquad \qquad \alpha_i = \rho_j \boldsymbol{s}_j^T \boldsymbol{q}_{i+1} ;$
$\qquad \qquad \boldsymbol{q}_i = \boldsymbol{q}_{i+1} - \alpha_i \boldsymbol{y}_j$
$\qquad \}$

Step 3 前向循环:
$\qquad \boldsymbol{r}_0 = D_0 \boldsymbol{q}_0 ;$
$\qquad FOR \quad i = 0,1,\cdots,L-2,L-1 \quad DO$
$\qquad \{$
$\qquad \qquad j = i + \delta ;$
$\qquad \qquad \beta_j = \rho_j \boldsymbol{y}_j^T \boldsymbol{r}_i ;$
$\qquad \qquad \boldsymbol{r}_{i+1} = \boldsymbol{r}_i + (\alpha_i - \beta_i)\boldsymbol{s}_j$
$\qquad \}$

最后算出的 $\boldsymbol{r}_L$ 即为 $H_k g_k$ 的值.

---

java 版本 L-BFGS 实现源码分析

L-BFGS 源码下载地址：https://github.com/vinhkhuc/lbfgs4j

我们从 test 目录下的com.github.lbfgs4j.LbfgsTest 测试类的 rosenbrock() 方法开始分析。

//创建函数    
Function f = new Function() {
  public int getDimension() {
  }
  public double valueAt(double[] x) {
  }
  public double[] gradientAt(double[] x) { 
  }
};
boolean verbose = true;
// 创建 Lbfgs 优化器
LbfgsMinimizer minimizer = new LbfgsMinimizer(verbose);
//得到最小值点的坐标
double[] x = minimizer.minimize(f);
//最小值点的函数值
double min = f.valueAt(x);

源码这里使用的是 rosenbrock函数:

$$\begin{array} & f(x,y) &=& (1 - x)^2 + 100*(y-x^2)^2 \\ \frac{\partial f(x,y)}{\partial x} &=& -2*(1 - x) - 400*(y - x^2)*x \\ \frac{\partial f(x,y)}{\partial y} &=& 200*(y - x^2) \end{array}$$

类 LbfgsMinimizer 的构造方法主要是设置了 L-BFGS 优化算法的基本参数，暂时先不看。

下面主要分析 LbfgsMinimizer 类的 minimizer.minimize(f) 方法.

  public double[] minimize(Function f, double[] x0) {
  //函数的维度，这里考虑的 (x,y) 两维
    int dim = f.getDimension();
    double[] x = x0 != null? x0 : new double[dim];
    MutableDouble fx  = new MutableDouble();
    // 评估器是为了获取参数函数的函数值和梯度
    Evaluate eval     = new Evaluate(f);
    Progress progress = verbose? new Progress() : null;
    // Start the L-BFGS optimization; this will invoke 
    // the callback functions evaluate() and progress() when necessary.
    Lbfgs.lbfgs(dim, x, fx, eval, progress, null, param);
    return x;
  }

接下来重点看 L-BFGS 优化过程了。

public static ReturnValue lbfgs(
        int n,
        double[] x,
        MutableDouble ptr_fx,
        LBFGS_Evaluate proc_evaluate,
        LBFGS_Progress proc_progress,
        Object instance,
        LBFGS_Param _param){
    ...
    //构建 LBFGS 优化参数
    LBFGS_Param param = _param != null? _param : _defparam;
    int m = param.m;
    ......
    //线性搜寻器
    LineSearchProc linesearch = new LineSearchMorethuente();
    ......
    /* Store the current position and gradient vectors. */
    veccpy(xp, x, n);
    veccpy(gp, g, n);
    /* 寻找最优步. */
    if (param.orthantwise_c == 0.) {
       //通过线性搜寻计算梯度 g
       ls = linesearch.eval(n, x, fx, g, d, step, xp, gp, w, cd, param);
    }......
    ......
    for(;;){
        //最后一次迭代保存数据的对象
        it = lm[end];
        /**
        *  Update vectors s and y:
        *      s_{k+1} = x_{k+1} - x_{k} = \step * d_{k}.
        *      y_{k+1} = g_{k+1} - g_{k}.
        */
        vecdiff(it.s, x, xp, n);
        vecdiff(it.y, g, gp, n);
        /**
        *  Compute scalars ys and yy:
        *      ys = y^t \cdot s = 1 / \rho.
        *      yy = y^t \cdot y.
        *  Notice that yy is used for scaling the hessian matrix H_0 (Cholesky factor).
        */
        ys = vecdot(it.y, it.s, n);
        yy = vecdot(it.y, it.y, n);
        it.ys = ys;
        /**
        *  Recursive formula to compute dir = -(H \cdot g).
        *  正如上面理论部分讲到的过程，这里是初始化步
        */
        bound = (m <= k) ? m : k;
        ++k;
        end = (end + 1) % m;    //这里的 delta 应该与上面理论部分的过程有点出入
        /* Compute the steepest direction. */
        if (param.orthantwise_c == 0.) {
            /* 计算负梯度. */
            vecncpy(d, g, n);
        } ......
        //这是后向循环处代码
        j = end;
        for (i = 0;i < bound;++i) {
            j = (j + m - 1) % m;    /* if (--j == -1) j = m-1; */
            it = lm[j];
            /* \alpha_{j} = \rho_{j} s^{t}_{j} \cdot q_{k+1}. */
            it.alpha = vecdot(it.s, d, n);
            it.alpha /= it.ys;
            /* q_{i} = q_{i+1} - \alpha_{i} y_{i}. */
            vecadd(d, it.y, -it.alpha, n);
        }   //这里跟上面理论中的公式一样
        //这里到 前向循环的初始化步得到 r_0，不过笔者没看明白这里为什么要缩放 ys/yy
        vecscale(d, ys / yy, n);
        //前向循环
        for (i = 0;i < bound;++i) {
            it = lm[j];
            /* \beta_{j} = \rho_{j} y^t_{j} \cdot r_{i}. */
            beta = vecdot(it.y, d, n);
            beta /= it.ys;
            /* r_{i+1} = r_{i} + (\alpha_{j} - \beta_{j}) s_{j}. */
            vecadd(d, it.s, it.alpha - beta, n);
            j = (j + 1) % m;        /* if (++j == m) j = 0; */
        }
        ......
    }
}

上面列出了核心步以及其注释，代码中省略了很多变量的初始化，以及变量取值范围的检查。

核心 L-BFGS 迭代过程就是如上面 for(;;){} 循环中的代码所示，不过核心的步骤跟上面理论算法过程一致.

参考

• http://blog.csdn.net/itplus/article/details/21896453

• https://www.cnblogs.com/pinard/p/5970503.html

• http://blog.csdn.net/google19890102/article/details/17842831