机器学习篇

GBDT（梯度提升决策树）

GBDT（Gradient Boosting Decision Tree）又叫 MART（Multiple Additive Regression Tree），是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终结果.

要理解 GBDT，就要先理解 GB ，然后才是 DT，而且这里的 DT 是回归树，而不是分类树.

DT（决策回归树）

这里先补充一下什么是回归树，因为之前所讲的决策树都是属于分类树.

先回顾下分类树:

我们知道 分类树在每次分枝时，是穷举每一个 feature 的每一个阈值，找到使得按照 `feature <= 阈值`和`feature > 阈值`分成两枝的熵最大的 feature 和阈值，按照该标准分枝得到的两个新节点，按同样的方法递归分裂下去，直到所有样本都被分入唯一的叶子节点，或达到预设的终止条件（如果叶子节点的样本不唯一，则以多数类作为叶子节点的分类结果）.

回归树大致流程类似:

不过在每个节点（不一定是叶子节点）都会得到一个预测值，以人的年龄为例，该预测值等于属于这个节点的所有人的年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）平方的总和除以 N（总人数），或者说是每个人的预测误差平方和 除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。直到每个叶子节点上人的年龄都唯一，或者达到预设终止条件，若最终叶子节点上的人的年龄不唯一，就以该节点上所有人的平均年龄作为该叶子节点的预测值.

就是分类树是按多数投票，以多数类的类别标号作为叶子节点的分类类别；回归树是按叶子节点的样本平均值作为该节点的预测值.

---

GBDT 实例

GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。

比如以年龄预测的例子来说明，A 的真实年龄是 18 岁，但第一棵树的预测年龄是 12 岁，差了 6 岁，即残差为 6 岁。那么在第二棵树里我们把 A 的年龄设为 6 岁去学习，如果第二棵树真的能把 A 分到 6 岁的叶子节点，那累加两棵树的结论就是 A 的真实年龄；如果第二棵树的结论是 5 岁，则 A 仍然存在 1 岁的残差，第三棵树里 A 的年龄就变成 1 岁，继续学。

我们来详细的说一下这个例子，为简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图1所示结果：

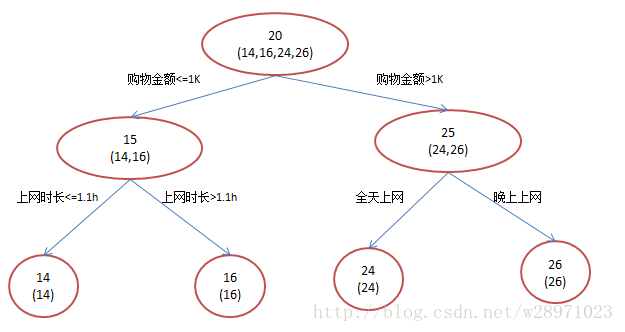
现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。我们会得到如下图2所示结果：

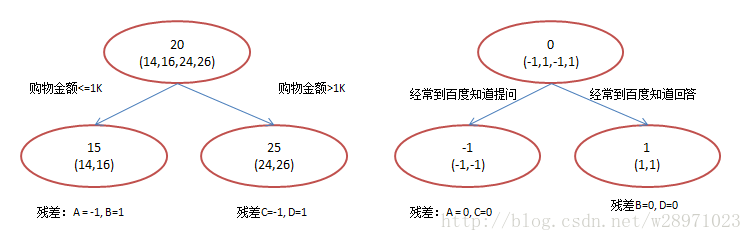
在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。

此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是 16-15=1（注意，A 的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是 15，如果还有树则需要都累加起来作为 A 的预测值）。进而得到 A,B,C,D 的残差分别为 (-1,1,-1,1)。

然后我们拿残差替代 A,B,C,D 的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值 1 和 -1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

换句话说，现在 A,B,C,D 的预测值都和真实年龄一致了。Perfect!：

A: 14 岁高一学生，购物较少，经常问学长问题；预测年龄 $A = 15 + (– 1) = 14$

B: 16 岁高三学生，购物较少，经常被学弟问问题；预测年龄 $B = 15 + 1 = 16$

C: 24 岁应届毕业生，购物较多，经常问师兄问题；预测年龄 $C = 25 + (–1) = 24$

D: 26 岁工作两年员工，购物较多，经常被师弟问问题；预测年龄 $D = 25 + 1 = 26$

那么哪里体现了Gradient呢？其实回到第一棵树结束时想一想，无论此时的cost function是什么，是均方差还是均差，只要它以误差作为衡量标准，残差向量 (-1, 1, -1, 1) 都是它的全局最优方向，这就是Gradient。

其实 GBDT 大致的过程就是这例子中所讲的，下面我们再做一些深入的理解

---

GBDT 深入理解

前面说了，GBDT 是先有 GB（梯度提升），再有 DT（决策树），所以我们先从 GB 讲起.

Boosting

boosting 在前面讲 AdaBoost提升算法的时候讲了，就是通过训练多个弱分类器来组合成一个强分类器，形式如下:

$$F_m(x) = f_0 + \alpha_1 f_1(x) + \alpha_2 f_2(x) + \cdots + \alpha_m f_m(x)$$ 其中，$f_i(x),i = 1,2,\cdots,m$ 是弱分类器，比如在 AdaBoost提升中是 C4.5决策树；$F_m(x)$ 是最终得到的强分类器.

---

Gradient Boosting Modeling

给定一个问题，我们如何构造这些弱分类器呢？

Gradient Boosting Modeling （梯度提升模型） 就是构造这些弱分类器的一种方法。它指的不是某个具体的算法，而是一种思想.

我们先从普通的梯度优化问题入手来理解:

$$find \ \hat{x} = arg \min_{x} f(x)$$ 针对这种问题，有个经典的算法叫 Steepest Gradient Descent，也就是最深梯度下降法。算法的大致过程是:

1. 给定一个起始点 $x_0$

2. 对 $i = 1,2,\cdots,K$ 分别做如下迭代:
   $\qquad x_i = x_{i-1} + \gamma_{i-1} \times g_{i-1}$，
   其中 $g_{i-1} = -\frac{\partial f}{\partial x} |_{x = x_{i-1}}$ 表示 $f$ 在 $x_{i-1}$ 点的梯度

3. 直到 $|g_{i-1}|$ 足够小，或者是 $|x_i - x_{i-1}|$ 足够小

以上迭代过程可以理解为: 整个寻优的过程就是小步快跑的过程，每跑一小步，都往函数当前下降最快的那个方向走一点，直到达到可接受的点.

我们将这个迭代过程展开得到寻优的结果:

$$x_k = x_0 + \gamma_1 g_1 + \gamma_2 g_2 + \cdots + \gamma_k g_k$$ 这个形式是不是与最开始我们要求的 $F_m(x)$ 类似；构造 $F_m(x)$ 本身也是一个寻优的过程，只不过我们寻找的不是一个最优点，而是一个最优的函数。

---

寻找最优函数这个目标，也是定义一个损失函数来做:

$$find \ F_m = arg \ \min_{F} L(F) = arg \ \min_{F} \sum_{i=0}^N Loss(F(x_i),y_i)$$ 其中，$Loss(F(x_i),y_i)$ 表示损失函数 $Loss()$ 在第 $i$ 个样本上的损失值，$x_i,y_i$ 分别表示第 $i$ 个样本的特征和目标值.

类似最深梯度下降法，我们可以通过梯度下降法来构造弱分类器 $f_1,f_2,\cdots,f_m$，只不过每次迭代时，令:

$$g_i = -\frac{\partial L}{\partial F}|_{F=F_{i-1}}$$ 即损失函数 $L()$ 对 $F$ 求取梯度.

但是函数对函数求导不好理解，而且通常都无法通过上述公式直接求解。于是就采取一个近似的方法，把函数 $F_{i-1}$ 理解成在所有样本上的离散的函数值，即:

$$\left[ F_{i-1}(x_1),F_{i-1}(x_2),\cdots,F_{i-1}(x_N) \right]$$ 这是一个 $N$ 维向量，然后计算: $$\hat{g}_i(x_k) = -\frac{\partial L}{\partial F(x_k)}|_{F = F_{i-1}},k = 1,2,\cdots,N$$ 这是一个函数对向量的求导，得到的也是一个梯度向量。注意，这里求导时的变量还是函数F，不是样本 $x_k$，只不过对 $F(x_k)$ 求导时，其他的 $x_i$ 都可以看成常数。

严格来说 $\hat{g}_i(x_k),k = 1,2,\cdots,N$ 只是描述了 $g_i$ 在某些个别点（所有的样本点）上值（连续函数上的离散点），并不足以表达 $g_i$，但我们可以通过函数拟合的方式从 $\hat{g}_i(x_k)$ 构造 $g_i$，这样我们就通过近似的方法得到函数对函数的导数了.

因此，GBM 的过程可以总结为:

1. 选择一个起始常量函数 $f_0$

2. 对 $i=1,2,\cdots,K$ 分别做如下迭代:

   (a) 计算离散梯度值 $\hat{g}_{i-1}(x_j) = -\frac{\partial L}{\partial F(x_j)}|_{F = F_{i-1}},j = 1,2,\cdots,N$

   (b) 对 $\hat{g}_{i-1}(x_j)$ 做函数拟合得到 $g_{i-1}$

   (c) 通过 line search 得到 $\gamma_{i-1} = arg \ \min L(F_{i-1} + \gamma_{i-1} g_{i-1})$

   (d) 令 $F_i = F_{i-1} + \gamma_{i-1} g_{i-1}$

3. 直到 $|\hat{g}_{i-1}|$ 足够小，或者迭代次数完毕

这里常量函数 $f_0$ 通常取样本目标值的均值，即

$$f_0 = \frac{1}{N} \sum_{i=0}^N y_i$$

---

Gradient Boosting Decision Tree

在上述算法过程中，如何通过 $\hat{g}_{i-1}(x_j),j = 1,2,\cdots,N$ 构造拟合函数 $g_{i-1}$ 呢，这里我们用的就是 Decision Tree（决策树）了.

所以理解 GBDT，重点是先理解 Gradient Boosting，其次才是 Decision Tree；也就是说 GBDT 是 Gradient Boosting 的一种具体实现，这个拟合函数也可以改用其他的方法，只不过决策树好用一点。

---

损失函数

谈到 GBDT 常听到的一种描述是 先构造一个(决策)树，然后不断在已有模型和实际样本输出的残差上再构造一棵树，依次迭代；其实这个说法不全面，尽管在本篇开头的那个 GBDT 的例子中是这样描述的，但拟合残差只是 GDBT 的一种特殊情况，下面对损失函数进行解释就清楚了.

从对 GBM 的描述里可以看到 Gradient Boosting 过程和具体用什么样的弱分类器是完全独立的，可以任意组合，因此这里不再刻意强调用决策树来构造弱分类器，转而我们来仔细看看弱分类器拟合的目标值，即梯度 $\hat{g}_{i-1}(x_j)$，之前我们已经提到过

$$\hat{g}_i(x_k) = -\frac{\partial L}{\partial F(x_k)}|_{F = F_{i-1}},k = 1,2,\cdots,N$$ 因此 $\frac{\partial L}{\partial F(x_k)}$ 很重要，以平方差损失函数为例，得: $$\frac{\partial L}{\partial F(x_k)}|_{F = F_{i-1}} = 2(F_{i-1}(x_k) - y_k)$$ 忽略 2 倍，后面括号中正是当前已经构造好的函数 $F_{i-1}$ 在样本上和目标值 $y_k$ 之间的差值.

如果我们换一个损失函数，比如绝对差:

$$Loss(F(x_i),y_i) = |F(x_i) - y_i|$$ 这个损失函数的梯度是个符号函数: $$\frac{\partial L}{\partial F(x_k)}|_{F = F_{i-1}} = sign(F_{i-1}(x_k) - y_k)$$ 由此可以看到，只有当损失函数为平方差函数时，才能说 GBDT 是通过拟合残差来构造弱分类器的，比如上面说的对残差不断的用决策回归树来拟合.

符号函数: http://blog.sina.com.cn/s/blog_455c7a600101nff3.html

---

GBDT 的推导

这里先给出原始 GBDT 的完整算法框架，然后详细演示 xgboost 中的实现推导过程，在下一小节中结合 xgboost 的 java 实现代码对照其推导过程进行分析.

GBDT 原始版本的算法框架:

输入: $\{ (x_i,y_i) \}_1^N, K,L,\cdots$
1. 初始化 $f_0$
2. $for \quad k = 1 \ to \ K \quad do$
3. $\qquad \hat{y}_i = -\frac{\partial L(y_i,F_{k-1}(x_i))}{\partial F_{k-1}},i = 1,2,\cdots,N$
4. $\qquad \{R_j,b_j\}_1^{J^*} = arg \min_{\{R_j,b_j\}_1^J} \sum_{i=1}^N \left[ \hat{y}_i - f_k(x_i;\{R_j,b_j\}_1^J) \right]^2$
5. $\qquad \begin{array} & \rho^{*} &= arg \min_{\rho} L\left( \{ y_i,F_{k-1}(x_i) + \rho f_k(x_i) \}_1^N \\ = arg \min_{\rho} \sum_{i=1}^N L\left( y_i,F_{k-1}(x_i) + \rho f_k(x_i) \right) + \Omega(f_k) \right) \end{array}$
6. $\qquad 令 \ f_k = \rho^* f_k,F_k = F_{k-1} + f_k$
7. $end$

其中：

• $\{(x_i,y_i)\}_1^N$ 表示 $N$ 个样本；

• $f_k$ 表示第 $k$ 棵决策树，这棵决策树的预测值为 $f_k = \sum_{j=1}^J b_j$；

• $K$ 表示总共要生成的决策树数量；

• $J$ 表示叶子节点的数量；

• $F_{k-1}(x_i)$ 表示前 $k-1$ 棵决策树综合得到的结果，即 $F_{k-1} = \sum_{i=1}^{k-1} f_i$；

• $L(y_i,F_{k-1}(x_i))$ 表示损失函数；

• $\{R_j,b_j\}_1^J$ 表示一个划分，$R_j$ 表示叶子节点 $j$ 上的样本集合，$b_j$ 表示该叶子节点上的样本输出值.

该过程就是在函数空间的梯度下降，不断减去 $\frac{\partial L}{\partial F}$，就能得到 $\min_F L(F)$

下面解释一下上面的关键步骤:

第三步: $\hat{y}_i$ 被称作响应（response），它是一个和残差（$y_i - F_{k-1}(x_i)$）正相关的变量.

第四步: 使用平方误差训练一棵决策树 $f_k$，拟合数据 $\{x_i,\hat{y}_i\}_1^N$，注意这里是 $\hat{y}_i$，拟合的是残差.

第五步: 进行线性搜索（line search），有的称作 Shrinkage ；上一步的 $f$ 是在平方误差下学到的，这一步进行一次 line search，让 $f$ 乘以步长 $\rho$ 后最小化 $L$.

GBDT 就是一个不断拟合响应（比如残差）并叠加到 $F$ 上的过程，在这个过程中，残差不断减小，$Loss$ 不断接近最小值.

---

下面给出 xgboost 中的推导过程:

在 xgboost 中使用的正则化函数为:

$$\Omega(f_k) = \frac{\gamma}{2}J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2$$

在每次迭代中，我们是要求 $f_k$，使目标函数 $\cal{L}$ 最小:

$$\begin{array} & \cal{L}_k &=& \sum_{i=1}^N L\left( y_i,F_{k-1}(x_i) + \rho f_k(x_i) \right) + \Omega(f_k) \\ &=& \sum_{i=1}^N L\left( y_i,F_{k-1} + \rho f_k \right) + \Omega(f_k) \end{array}$$ 下面对损失函数在 $F_{k-1}$ 处 应用二级泰勒展开: $$\begin{array} & \because f(x) \approx f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0) \\ \therefore L\left( y_i,F_{k-1} + \rho f_k \right) \approx L(y_i,F_{k-1}) + \frac{\partial L(y_i,F_{k-1})}{\partial F_{k-1}} f_k + \frac{1}{2} \frac{\partial^2 L(y_i,F_{k-1})}{\partial F_{k-1}^2} f_k^2 \end{array}$$

如何理解泰勒展开:
https://www.zhihu.com/question/25627482

https://baike.baidu.com/item/%E6%B3%B0%E5%8B%92%E5%85%AC%E5%BC%8F/7681487?fr=aladdin

我们令:

$$\begin{array} & g_i &=& \frac{\partial L(y_i,F_{k-1})}{\partial F_{k-1}} \\ h_i &=& \frac{\partial^2 L(y_i,F_{k-1})}{\partial F_{k-1}^2} \end{array}$$

于是目标函数变成了:

$$\begin{array} & \cal{L}_k &\approx& \sum_{i=1}^N \left( L(y_i,F_{k-1}) + g_i f_k + \frac{1}{2} h_i f_k^2 \right) + \Omega(f_k) \\ &=& \sum_{i=1}^N \left( L(y_i,F_{k-1}) + g_i \sum_{j=1}^J b_j + \frac{1}{2} h_i \sum_{j=1}^J b_j^2 \right) + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \end{array}$$

对第 $k$ 次迭代来说，前面的 $k-1$ 次迭代得到的决策树都是已知的，即 $F_{k-1},g_i,h_i$ 都是已知的，则我们整理出与未知量有关的项:

$$\begin{array} & \cal{L}_k(\{b_j\}_1^J,\{R_j\}_1^J) &=& \sum_{i=1}^N \left( g_i \sum_{j=1}^J b_j + \frac{1}{2} h_i \sum_{j=1}^J b_j^2 \right) + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \\ &=& \sum_{x_i \in R_j} \left( g_i \sum_{j=1}^J b_j + \frac{1}{2} h_i \sum_{j=1}^J b_j^2 \right) + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \\ &=& \sum_{j=1}^J \left( \sum_{x_i \in R_j} g_i b_j + \sum_{x_i \in R_j} \frac{1}{2} h_i b_j^2 \right) + \frac{\gamma}{2} J + \frac{\lambda}{2} \sum_{j=1}^J b_j^2 \end{array}$$

对第 $k$ 棵决策树的叶子节点 $j$ 来说，它的划分与其他叶子节点无关，只与同属于本叶子节点的其他样本有关，所以这里才能将 $\sum_{i=1}^N$ 替换成 $\sum_{x_i \in R_j}$

我们令:

$$\begin{array} & G_j &=& \sum_{x_i \in R_j} g_i \\ H_j &=& \sum_{x_i \in R_j} h_i \end{array}$$

于是目标函数又改为了:

$$\cal{L}_k(\{b_j\}_1^J,\{R_j\}_1^J) = \sum_{j=1}^J \left( G_j b_j + \frac{1}{2}(H_j + \lambda) b_j^2 \right) + \frac{\gamma}{2} J$$

---

为了方便阐述问题，我们把问题分为两个子问题:

• 问题一: 如果已经得到了 $\{R_j\}_1^J$，最小化 $\cal{L}_k$ 的 $\{b_j\}_1^J$ 是多少？
  这个问题是为了在已经得到叶子节点的情况下，得到的最优目标函数值是多少.

• 问题二: 如果将当前节点 $R_i$ 分裂，应该在哪一个分裂点使得 $\cal{L}_k$ 最小？
  这个问题是为了解如何进行节点分裂.

---

下面分别针对这两个问题做解:

• 问题一
  这个比较好求，直接目标函数 $\cal{L}_k(\{b_j\}_1^J,\{R_j\}_1^J)$ 对 $b_j$ 求导，令结果为零:

  $$\frac{\partial \cal{L}_k(\{b_j\}_1^J,\{R_j\}_1^J)}{\partial b_j} = G_j + (H_j + \lambda)b_j = 0$$ 所以得: $$b_j^* = - \frac{G_j}{H_j + \lambda}, j = 1,2,\cdots,J$$ 此时最小的 $\cal{L}_k$ 是: $$\cal{L}_k^* = -\frac{1}{2}\sum_{j=1}^J \frac{G_j^2}{H_j + \lambda} + \frac{\gamma}{2} J$$

• 问题二
  求 $\{R_j\}_1^J$ 的方法是对输入 $x$ 所属空间的一种划分方法，不连续，无法求导. 取而代之的是使用贪心算法，即分裂某节点时，只考虑对当前节点分裂后，哪个分裂方案能得到最小的 $\cal{L}_k$ .

  假设欲将当前节点 $R_j$ 分裂成 $R_L,R_R$ 这两个子节点，且要使得分裂后整棵树的 $\cal{L}_k$ 最小；而整棵树的最小 $\cal{L}_k$ 等于每个叶子节点上最小的损失的和；又由于对节点 $R_j$ 的分裂过程只涉及到三个节点———— $R_j,R_L,R_R$，所以这个目标可以换一种描述.

  这个问题的目标可以描述为:

  $$\max_{R_L,R_R} \cal{L}^* - \left( \cal{L}_L^* + \cal{L}_R^* \right)$$ 其中，$\cal{L}^*$ 为分裂前节点 $R_j$ 对应的最小损失，$\cal{L}_L^* , \cal{L}_R^*$ 分别为分裂后左右子节点对应的最小损失.

  这个目标函数可直观的解释为: 分裂后的损失和 要小于分裂前的损失，这样节点分裂才能使整棵树的损失降低，节点分裂才有意义，而且这个降低的幅度越大越好.

  利用问题一的结论，则目标函数写为:

  $$\begin{array} & \cal{T} &=& \max_{R_L,R_R} \cal{L}^* - \left( \cal{L}_L^* + \cal{L}_R^* \right) \\ &=& \max_{R_L,R_R} \left( -\frac{1}{2} \frac{(G_L + G_R)^2}{H_L + H_G + \lambda} + \frac{\gamma}{2} \right) + \left( -\frac{1}{2} \frac{G_L^2}{H_L + \lambda} + \frac{\gamma}{2} \right) + \left( -\frac{1}{2} \frac{G_R^2}{H_R + \lambda} + \frac{\gamma}{2} \right) \\ &=& \max_{R_L,R_R} \frac{1}{2} \left( \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_G + \lambda} + \gamma \right) \\ &=& \max_{R_L,R_R} \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_G + \lambda} \end{array}$$

---

于是以平方误差损失函数为例进一步细化推导:

$$L = \frac{(y - F(x))^2}{2}$$ 于是对 $F$ 求一阶导得到响应（此时响应 = 残差）: $$\hat{y}_i = -g_i = -\frac{\partial L(y_i,F(x_i))}{\partial F} = y_i - F(x_i)$$ 求二阶导是: $$h_i = 1$$

---

于是树的分裂算法过程为:

输入: $R_j$，落在 $R_j$ 的训练样本 $\{(x_i^{(j)},y_i^{(j)})\}_1^N,\cdots$，其中 $x_i^{(j)} \in \cal{R}^m$
$\qquad decr = 0,G = \sum_{i=1}^N g_i,H = \sum_{i=1}^N h_i$

$for \quad k = 1 \ to \ m \quad do$
$\qquad G_L = 0,H_L = 0$
$\qquad for \ l \ in \ uniq(sorted(\{x_{ik}^{(j)}\})) \quad do$
$\qquad \qquad G_L = G_L + g_l,H_L = H_L + h_l$
$\qquad \qquad G_R = G - G_L,H_R = H + H_L$
$\qquad \qquad decr = \max \left( decr, \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_G + \lambda} \right)$
$\qquad end$
$end$

$if \quad decr < 0 \ or \ 满足终止条件 \quad then$
$\qquad 输出: 保持 \ $R_j$\ 不分裂$
$end$

输出: 按照最大 decr 的方案将 $R_j$ 分裂成 $R_L$ 和 $R_R$.

该算法做的事情就是求使 $\cal{T}$ 最大的分裂 $R_L,R_R$:

• $k = 1,2,\cdots,m$ 表示 $m$ 个属性，循环遍历每个属性，这就决策树寻找最优划分属性一样的过程.

• $uniq(sorted(\{x_{ik}^{(j)}\}))$ 表示对叶子节点 $R_j$ 上的样本按属性 $k$ 进行排序去重.

• 二重循环里面的三句就是为了求上式目标函数 $\cal{T}$.

---

基于上面的树分裂算法，完整的 GBDT 算法描述为:

输入: $\{(x_i,y_i)\}_1^N,K,\cdots$
1. 初始化 $f_0$
2. $for \quad k = 1 \ to \ K \quad do$
3. $\qquad$ 根据具体的损失函数计算出 $\hat{y}_i,i = 1,2,\cdots,N$
4. $\qquad$ 由上述树生成算法得到 $\{R_j\}_1^J,\{b_j\}_1^J$，从而得到 $f_k$，其中 $g_j,h_j$ 根据具体的损失函数 $L$ 计算.
5. $\qquad$ 令 $F_k = F_{k-1} + f_k$
6. $end$

这个就没什么好说的了，就是不断的计算上一步的损失，然后用上面的树生成算法对上一步迭代的损失进行拟合，然后把这一步生成的决策树累加到 $F$ 上.

还有损失函数为 Logistic Loss 的，即 logistic regression 中使用的交叉熵 Loss，这个只能用于分类，读者有兴趣可以自行查询学习.

---

R 版本的 xgboost 应用

install.packages("xgboost")
# https://www.cnblogs.com/payton/p/5340538.html
dataset <- read.table("http://archive.ics.uci.edu/ml/machine-learning-databases/credit-screening/crx.data", sep = ",", na.strings = "NA")
head(dataset)
sapply(dataset,function(x) sum(is.na(x)))
sapply(dataset,class)
set.seed(123)
dataset  = na.omit(dataset)
n = dim(dataset)[1]
index = sample(n,round(0.7*n))
train = dataset[index,]
test = dataset[-index,]
dim(train)
dim(test)
dataset2 = dataset
library(plyr)
into_factor = function(x){
  if(class(x) == "factor"){
    n = length(x)
    data.fac = data.frame(x = x,y = 1:n)
    output = model.matrix(y ~ x,data.fac)[,-1]
  }else{
    output = x
  }
  output
}
head(dataset$V4)
into_factor(dataset$V4)[1:5,]
dataset2 = colwise(into_factor)(dataset2)
dataset2 = do.call(cbind,dataset2)
dataset2 = as.data.frame(dataset2)
head(dataset2)
dim(dataset2)
library(xgboost)
set.seed(123)
index = sample(n,round(0.7*n))
train.xg = dataset2[index,]
test.xg = dataset2[-index,]
label <- as.matrix(train.xg[,38,drop = F])
head(label)
data <- as.matrix(train.xg[,-38,drop = F])
data2 <- as.matrix(test.xg[,-38,drop = F])
label2 <- as.matrix(test.xg[,38,drop = F])
xgmat <- xgb.DMatrix(data, label = label, missing = -10000)
param <- list("objective" = "binary:logistic","bst:eta" = 1,"bst:max_depth" = 2,"eval_metric" = "logloss","silent" = 1,"nthread" = 16 ,"min_child_weight" =1.45)
nround =275
bst = xgb.train(param, xgmat, nround )
res1 = predict(bst,data2)
pre1 = ifelse(res1>0.5,1,0)
table(pre1,label2)
accurancy4 = mean(pre1 == label2)
accurancy4

参考至: https://www.cnblogs.com/payton/p/5340538.html

http://blog.csdn.net/q383700092/article/details/51546380

---

xgboost源码分析

https://github.com/komiya-atsushi/xgboost-predictor-java

---

小结

参考博文:

• https://www.cnblogs.com/bentuwuying/p/6667267.html

• https://www.cnblogs.com/peizhe123/p/5086128.html

• http://www.flickering.cn/machine_learning/2016/08/gbdt%E8%AF%A6%E8%A7%A3%E4%B8%8A-%E7%90%86%E8%AE%BA/