@Dmaxiya 2018-08-18T13:06:27.000000Z 字数 7522 阅读 1288

Codeforces Round #504 (Div. 1 + Div. 2)

Codeforces

Contests 链接：Codeforces Round #504 (Div. 1 + Div. 2)
过题数：3
排名：1013/7459

A. Single Wildcard Pattern Matching

题意

给定两个字符串 $s$ 和 $t$ ，长度分别为 $n$ 和 $m$ ， $s$ 串中最多含有一个 * 通配符，通配符可以用任意字符串（也可能为空）替换，问能否将其中的通配符用某个字符串替换后，使 $s$ 与 $t$ 串相等。

输入

第一行为两个整数 $n,m~(1\leq n,m\leq2\times10^5)$ ，第二行为一个长度为 $n$ 的字符串 $s$ ，第三行为一个长度为 $m$ 的字符串 $t$ ， $s$ 串中只含有小写字母与最多一个 * 字符， $t$ 串只包含小写字母。

输出

如果 $s$ 串可以转化为 $t$ 串，则输出 $YES$ ，否则输出 $NO$ 。

样例

输入
6 10 code*s codeforces
输出
YES
提示
将 `*` 改为 `force` 就可以令两个字符串相等。

输入
6 5 vk*cup vkcup
输出
YES
提示
用空串代替 `*` 就可以令两个字符串相等。

输入
1 1 v k
输出
NO
提示
两个字符串不相等，故答案为 $NO$ 。

输入
9 6 gfgf*gfgf gfgfgf
输出
NO
提示
不论用什么字符串替换 `*` 都无法使两个字符串相等。

题解

如果 $s$ 串不包含通配符，直接用 $strcmp$ 比较，否则从前往后、从后往前与 $t$ 串进行比较，记录 $t$ 串的分隔位，如果 $s$ 串的 * 之前与 $t$ 的公共前缀与 * 之后与 $t$ 的公共后缀不相交，就输出 $YES$ ，否则输出 $NO$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <cmath>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 200000 + 100;
int n, m;
char s[maxn], t[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("10.out", "w", stdout);
    #endif // Dmaxiya
    while(scanf("%d%d", &n, &m) != EOF) {
        int l, r;
        int tl, tr;
        bool flag = false;
        scanf("%s%s", s, t);
        for(int i = 0; i < n; ++i) {
            if(s[i] == '*') {
                flag = true;
                l = i - 1;
                r = i + 1;
            }
        }
        if(!flag) {
            if(strcmp(s, t) == 0) {
                printf("YES\n");
            } else {
                printf("NO\n");
            }
            continue;
        }
        tl = -1;
        tr = m;
        for(int i = 0; i <= l; ++i) {
            if(s[i] != t[i]) {
                flag = false;
                break;
            }
            tl = i;
        }
        for(int i = 1; n - i >= r; ++i) {
            if(s[n - i] != t[m - i]) {
                flag = false;
                break;
            }
            tr = m - i;
        }
        if(flag) {
            if(tl < tr) {
                printf("YES\n");
            } else {
                printf("NO\n");
            }
        } else {
            printf("NO\n");
        }
    }
    return 0;
}

B. Pair of Toys

题意

有 $n$ 个玩具，第 $i$ 个玩具的价格为 $i$ ，问有多少对玩具 $(a,b)~(a\neq b)$ ，它们的价值和等于 $k$ ，其中 $(a,b)$ 和 $(b,a)$ 被认为是相同的玩具对。

输入

输入只包含两个整数 $n,k~(1\leq n,k\leq10^{14})$ 。

输出

输出满足条件的玩具对数。

样例

输入
8 5
输出
2
提示
$(1,4)$ 和 $(2,3)$ 都是合法的选择。

输入
8 15
输出
1
提示
只有 $(7,8)$ 是合法的选择。

输入
7 20
输出
0
提示
$1$ 到 $7$ 中所有数字相加都不能达到 $20$ ，因此答案为 $0$ 。

输入
1000000000000 1000000000001
输出
500000000000
提示
我们可以选择 $(1,1000000000000),(2,999999999999),(3,999999999998),\cdots,(500000000000,500000000001)$ ，总共有 $500000000000$ 对整数。

题解

先确定所有可选数字的右边界 $R=\min(k-1,n)$ ，再确定其左边界 $L=\max(1,k-R)$ ，其中满足条件的整数对数为 $\lfloor\frac{R-L+1}{2}\rfloor$

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <cmath>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <algorithm>
using namespace std;
#define LL long long
LL n, k;
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("10.out", "w", stdout);
    #endif // Dmaxiya
    while(scanf("%I64d%I64d", &n, &k) != EOF) {
        LL R = min(k - 1, n);
        LL L = max(1LL, k - R);
        if(L >= R) {
            printf("0\n");
            continue;
        }
        printf("%I64d\n", (R - L + 1) / 2);
    }
    return 0;
}

C. Bracket Subsequence

题意

给定一个长度为 $n$ 的合法括号序列，其中的左右括号能完全匹配，要求从中找到一个长度为 $k$ 的合法括号子序列。

输入

第一行为两个整数 $n,k~(2\leq k\leq n\leq2\times10^5)$ ，其中 $n$ 和 $k$ 都是偶数，第二行为一个长度为 $n$ 的字符串，字符串保证是一个合法的括号序列。

输出

输出长度为 $k$ 的合法括号子序列。

样例

输入
6 4 `()(())`
输出
`()()`

输入
8 8 `(()(()))`
输出
`(()(()))`

题解

用栈模拟括号匹配的过程，其中弹出栈的必然是合法的括号序列，将弹出栈的括号下标标记，当弹出栈的括号个数达到 $k$ 时，将所有标记的括号输出。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <cmath>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 200000 + 100;
int n, k, top;
char str[maxn];
bool vis[maxn];
int sta[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("10.out", "w", stdout);
    #endif // Dmaxiya
    while(scanf("%d%d", &n, &k) != EOF) {
        top = 0;
        memset(vis, 0, sizeof(vis));
        scanf("%s", str);
        for(int i = 0; i < n; ++i) {
            if(str[i] == '(') {
                sta[top++] = i;
            } else {
                --top;
                vis[sta[top]] = true;
                vis[i] = true;
                k -= 2;
                if(k == 0) {
                    break;
                }
            }
        }
        for(int i = 0; i < n; ++i) {
            if(vis[i]) {
                printf("%c", str[i]);
            }
        }
        printf("\n");
    }
    return 0;
}

D. Array Restoration

题意

有一个长度为 $n$ 的序列，可以对这 $n$ 个序列进行 $q$ 次操作，第 $i$ 次操作选择一个区间 $[l_i,r_i]$ ，将这个区间内的所有数字用 $i$ 替换，每个位置上的数字至少被一个区间覆盖，最后将这个序列中的某几个数字改为 $0$ 。现在题目给出最终的序列，问是否存在合法的 $q$ 次操作，能够得到给出的序列，求 $q$ 次操作后（将序列某些数字变为 $0$ 之前）的序列。

输入

第一行为两个整数 $n,q~(1\leq n,q\leq2\times10^5)$ ，第二行为 $n$ 个整数 $a_1,a_2,\cdots,a_n~(0\leq a_i\leq q)$ 。

输出

如果给出的序列无法从上面的操作中得到，输出 $NO$ ，否则在第一行输出 $YES$ ，第二行输出 $q$ 次操作之后的 $n$ 个整数。

样例

输入
4 3 1 0 2 3
输出
YES 1 2 2 3
提示
将 $0$ 用 $1$ 替换也是合法的，但是用 $3$ 替换是不合法的。

输入
3 10 10 10 10
输出
YES 10 10 10
提示
不论前 $q-1$ 次操作是怎么样，第 $q$ 次操作是选择区间 $[1,3]$ 即可。

输入
5 6 6 5 6 2 2
输出
NO
提示
由于第 $5$ 次操作必须在第 $6$ 次操作之前，所以不可能先将区间 $[1,3]$ 更新为 $6$ 之后再将区间 $[2,2]$ 更新为 $5$ 。

输入
3 5 0 0 0
输出
YES 5 4 2
提示
有许多种操作对于 $0~0~0$ 而言都是合法的。

题解

由于数字大的一定比数字小的后更新，所以每个数字出现的左端点与右端点之间的数字不能小于它自身，可以用线段树维护最小值，从 $q$ 到 $1$ 询问第 $i$ 个数字出现的左端点 $L_i$ 与右端点 $R_i$ ，如果在查询区间最小值时遇到 $0$ 的情况，就向下将 $0$ 更新为当前数字再进行查询。记得首先查询序列内是否有数字 $q$ ，如果没有数字 $q$ 就将其中任意一个 $0$ 修改为 $q$ ，如果无法修改则直接输出 $NO$ 。所有询问与更新结束后，如果序列中仍含有 $0$ ，就将所有 $0$ 赋值为 $1$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <cmath>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 200000 + 100;
int n, q;
int num[maxn], L[maxn], R[maxn];
int Min[maxn << 2];
void push_up(int rt) {
    Min[rt] = min(Min[rt << 1], Min[rt << 1 | 1]);
}
void build(int l, int r, int rt) {
    if(l == r) {
        Min[rt] = num[l];
        return ;
    }
    int m = (l + r) >> 1;
    build(l, m, rt << 1);
    build(m + 1, r, rt << 1 | 1);
    push_up(rt);
}
void update(int x, int l, int r, int rt) {
    if(l == r) {
        Min[rt] = x;
        num[l] = x;
        return ;
    }
    int m = (l + r) >> 1;
    if(Min[rt << 1] == 0) {
        update(x, l, m, rt << 1);
    }
    if(Min[rt << 1 | 1] == 0) {
        update(x, m + 1, r, rt << 1 | 1);
    }
    push_up(rt);
}
int query(int L, int R, int x, int l, int r, int rt) {
    if(L <= l && r <= R) {
        if(Min[rt] == 0) {
            update(x, l, r, rt);
        }
        return Min[rt];
    }
    int m = (l + r) >> 1;
    int ret = INT_MAX;
    if(L <= m) {
        ret = min(ret, query(L, R, x, l, m, rt << 1));
    }
    if(m < R) {
        ret = min(ret, query(L, R, x, m + 1, r, rt << 1 | 1));
    }
    push_up(rt);
    return ret;
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("10.out", "w", stdout);
    #endif // Dmaxiya
    while(scanf("%d%d", &n, &q) != EOF) {
        for(int i = 0; i <= q; ++i) {
            L[i] = n + 1;
            R[i] = 0;
        }
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
            L[num[i]] = min(L[num[i]], i);
            R[num[i]] = max(R[num[i]], i);
        }
        if(L[q] > R[q]) {
            if(L[0] != n + 1) {
                num[L[0]] = q;
                L[q] = R[q] = L[0];
            } else {
                printf("NO\n");
                continue;
            }
        }
        build(1, n, 1);
        bool flag = true;
        for(int i = q; i >= 1; --i) {
            if(L[i] > R[i]) {
                continue;
            }
            if(query(L[i], R[i], i, 1, n, 1) < i) {
                flag = false;
                break;
            }
        }
        if(!flag) {
            printf("NO\n");
            continue;
        }
        printf("YES\n");
        for(int i = 1; i <= n; ++i) {
            if(i != 1) {
                printf(" ");
            }
            if(num[i] == 0) {
                printf("1");
            } else {
                printf("%d", num[i]);
            }
        }
        printf("\n");
    }
    return 0;
}

E. Down or Right

题意

这是一道交互题，有一个 $n\times n$ 的网格，其中有一些网格是可以行走的，而有一些是无法行走的，在可以行走的网格中，下一步只能往右或下两个方向移动到下一格可以行走的网格中，但是我们并不知道这个网格哪些格子是可以行走的那些无法行走。 $Bob$ 要从 $(1,1)$ 点走到 $(n,n)$ 点，每次可以询问他从 $(x_1,y_1)$ 点是否能到达 $(x_2,y_2)$ 点， $Bob$ 将会回答 $YES$ 或者 $NO$ ，且每次询问 $(x_1,y_1)$ 与 $(x_2,y_2)$ 的哈密顿距离不能小于 $n-1$ ，最终输出从 $(1,1)$ 到 $(n,n)$ 的合法行走方案。询问的次数不能超过 $4n$ 。

输入

第一次输入为一个整数 $n~(2\leq n\leq500)$ ，后面的输入为 $YES$ 或者 $NO$ ，取决于输出的询问。

输出

如果为询问，则按照 $?~x_1~y_1~x_2~y_2$ 的格式询问，如果已经可以求得路径，则第一个字符为 !，空一格之后，输出 $2n-2$ 个字符，第 $i$ 个字符为 D 表示第 $i$ 步需要往下走，为 R 表示需要往右走。

样例

输入
4 YES NO YES YES
输出
? 1 1 4 4 ? 1 2 4 3 ? 4 1 4 4 ? 1 4 4 4 ! RDRRDD
提示
网格中的可行走方格与不可行走方格如下图：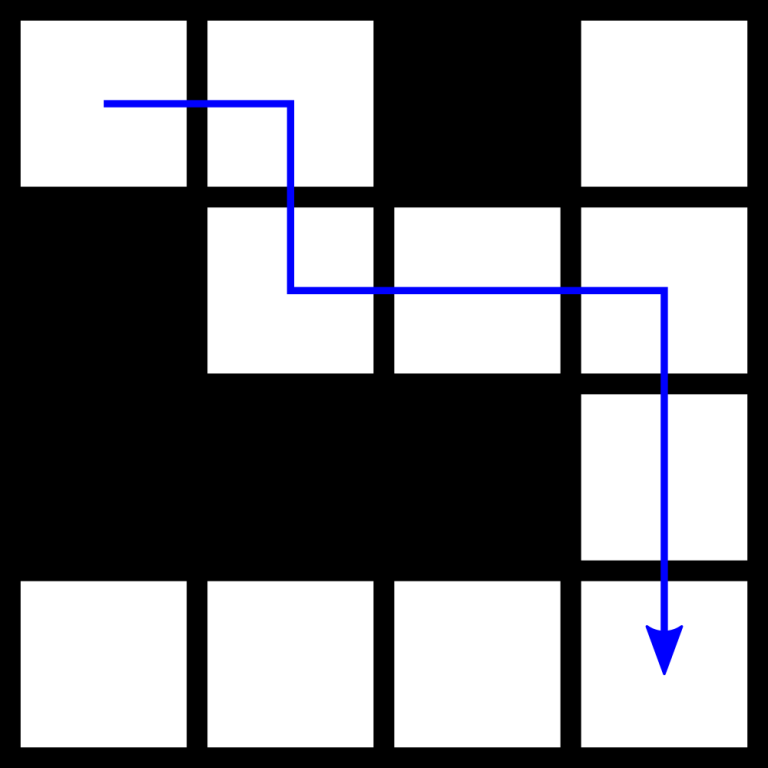

题解

如果“左上的点”表示与点 $(1,1)$ 的哈密顿距离不大于 $n-1$ 的所有点，“右下的点”表示与点 $(n,n)$ 的哈密顿距离不大于 $n-1$ 的点，则先从 $(1,1)$ 开始询问左上的点是否能到达 $(n,n)$ ，能往右就尽量往右走，再从 $(n,n)$ 开始询问 $(1,1)$ 能否到达右下的点，能往上就尽量往上，最后这两条路径一定会重合于某一点 $(x,y)$ ，其中 $x-1+y-1=n-x+n-y=n-1$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <cmath>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 20000 + 100;
int n, cntl, cntr;
char ret[10];
char ansl[maxn], ansr[maxn];
int dis(int x1, int y1, int x2, int y2) {
    return abs(x1 - x2) + abs(y1 - y2);
}
int main() {
    #ifdef Dmaxiya
//    freopen("test.txt", "r", stdin);
//    freopen("10.out", "w", stdout);
    #endif // Dmaxiya
    scanf("%d", &n);
    int x = 1, y = 1;
    while(dis(1, 1, x, y + 1) <= n - 1) {
        int xx = x;
        int yy = y + 1;
        printf("? %d %d %d %d\n", xx, yy, n, n);
        fflush(stdout);
        scanf("%s", ret);
        if(ret[0] == 'Y') {
            ansl[cntl++] = 'R';
            ++y;
        } else {
            ansl[cntl++] = 'D';
            ++x;
        }
    }
    x = y = n;
    while(dis(x - 1, y, n, n) <= n - 1) {
        int xx = x - 1;
        int yy = y;
        printf("? %d %d %d %d\n", 1, 1, xx, yy);
        fflush(stdout);
        scanf("%s", ret);
        if(ret[0] == 'Y') {
            ansr[cntr++] = 'D';
            --x;
        } else {
            ansr[cntr++] = 'R';
            --y;
        }
    }
    ansl[cntl] = '\0';
    printf("! %s", ansl);
    for(int i = cntr - 1; i >= 0; --i) {
        printf("%c", ansr[i]);
    }
    printf("\n");
    fflush(stdout);
    return 0;
}

Codeforces Round #504 (Div. 1 + Div. 2)

A. Single Wildcard Pattern Matching

题意

输入

输出

样例

题解

过题代码

B. Pair of Toys

题意

输入

输出

样例

题解

过题代码

C. Bracket Subsequence

题意

输入

输出

样例

题解

过题代码

D. Array Restoration

题意

输入

输出

样例

题解

过题代码

E. Down or Right

题意

输入

输出

样例

题解

过题代码

内容目录