@Dmaxiya 2018-08-17T10:16:59.000000Z 字数 8115 阅读 1030

Codeforces Round #469 (Div. 2)

Codeforces

Contests 链接：Codeforces Round #469 (Div. 2)
过题数：5
排名：72/9541

A. Left-handers, Right-handers and Ambidexters

题意

有 $l$ 个擅长使用左手的人， $r$ 个擅长使用右手的人，有 $a$ 个左右手都擅长的人，要求组建一支人数为人偶数的队伍，队伍中使用左手的人数和右手的人数一样多（每个人都只能使用其中一只自己擅长的手），求队伍的最大人数。

输入

输入只包含 $3$ 个整数 $l,r,a~(0\leq l,r,a\leq100)$ 。

输出

输出能组建的队伍的最大人数。

样例

输入	输出	提示
1 4 2	6	$6$ 个人中有 $1$ 个人只擅长使用左手， $2$ 个两只手都擅长的人只使用左手， $3$ 个擅长使用右手的人。
5 5 5	14	$14$ 个人中 $5$ 个人只擅长使用左手， $5$ 个人只擅长使用右手， $4$ 个两只手都擅长的人 $2$ 个人只使用右手， $2$ 个人只使用左手。
0 2 0	0

题解

先将 $a$ 个人分配给人数少的那一边，使得擅长左手的人数和擅长右手的人数尽量相等，如果还有多余人数，就自行两两组队。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <sstream>
using namespace std;
#define LL long long
int l, r, a;
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d%d", &l, &r, &a) != EOF) {
        if(l > r) {
            swap(l, r);
        }
        int ans = r - l;
        if(ans > a) {
            ans = 2 * (a + l);
        } else {
            ans = 2 * (ans + l) + (a - ans) / 2 * 2;
        }
        printf("%d\n", ans);
    }
    return 0;
}

B. Intercepted Message

题意

给定两个长度分别为 $n,m$ 的序列 $x_1,x_2,\cdots,x_n$ 和 $y_1,y_2,\cdots,y_m$ ，要将序列 $X$ 和序列 $Y$ 分别划分成若干段，使得序列 $X$ 的第 $i$ 段数字的和等于序列 $Y$ 的第 $i$ 段数字的和，问最多能够分成多少段。

输入

第一行为两个整数 $n,m~(1\leq n,m\leq10^5)$ ，第二行为 $n$ 个整数 $x_1,x_2,\cdots,x_n~(1\leq x_i\leq10^6)$ ，第三行为 $m$ 个整数 $y_1,y_2,\cdots,y_m~(1\leq y_i\leq10^6)$ ，数据保证 $\sum_{i=1}^nx_i=\sum_{i=1}^my_i$ 且 $\sum_{i=1}^nx_i\leq10^6$

输出

输出能够分割的最大段数。

样例

输入	输出	提示
7 6 2 5 3 1 11 4 4 7 8 2 4 1 8	3	$3$ 段数字分别为： $2+5= 7,15=3+1+11=8+2+4+1,4+4=8$ 。
3 3 1 10 100 1 100 10	2	可以将第 $1$ 个数字分为一段，后面 $2$ 个数字分为一段，由于不能修改数字的顺序，所以我们不能将 $1~10~100$ 分为 $3$ 段。
1 4 4 1 1 1 1	1	$A$ 序列只有一个数字，所以只能分成 $1$ 段。

题解

类似于归并排序，给两个序列各加一个指针，分别移动，哪一个序列加的数字小于另一个序列的数，就将那个序列的指针往后移动，每次移动到相等，就将答案 $+1$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
int n, m, cnt;
LL suma, sumb;
LL a[maxn], b[maxn];
int main() {
    #ifdef LOCAL
        freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &m) != EOF) {
        for(int i = 0; i < n; ++i) {
            scanf("%I64d", &a[i]);
        }
        for(int i = 0; i < m; ++i) {
            scanf("%I64d", &b[i]);
        }
        cnt = 0;
        int Index = 0;
        suma = sumb = 0;
        for(int i = 0; i < n; ++i) {
            suma += a[i];
            while(sumb < suma) {
                sumb += b[Index];
                ++Index;
            }
            if(sumb == suma) {
                ++cnt;
                suma = sumb = 0;
            }
        }
        printf("%d\n", cnt);
    }
    return 0;
}

C. Zebras

题意

给定一个 $01$ 字符串，要求找出其中满足下列条件的子序列：

子序列中 $01$ 相间；

子序列以 $0$ 开头，以 $0$ 结尾；

任意两个子序列之间没有交集；

所有子序列的并为整个序列。

输出找出的子序列方案，子序列的个数不必最少，只要合法即可。

输入

输入只有一行，为一个只包含 $0$ 和 $1$ 的字符串 $s~(1\leq|s|\leq2\times10^5)$ 。

输出

第一行输出一个整数 $k~(1\leq k\leq|s|)$ ，表示子序列的个数，接下去 $k$ 行，每行表示一个子序列，每行第一个整数为 $l_i~(1\leq l_i\leq|s|)$ ，表示第 $i$ 个子序列中的字符个数，接下去 $l_i$ 个整数每个整数表示序列中的第 $j$ 个元素在原字符串中的下标，下标从 $1$ 开始。如果无法构造出满足条件的序列，输出 $-1$ 。

样例

输入	输出
0010100	3 3 1 3 4 3 2 5 6 1 7
111	-1

题解

将所有 $0$ 字符所在的下标放到一个 $set$ 中，所有 $1$ 字符所在的下标放到一个 $set$ 中，每次交替从这两个 $set$ 中选出大于当前 $0$ 或者 $1$ 的下标的最小值，将这个下标记录到答案中，并从查找的集合中删去，如果某一次查找中，查找到的最后一个数字不是 $0$ ，则说明 $0$ 的数量不够，需要输出 $-1$ ，如果所有的 $01$ 间隔序列都查找完毕，而存 $1$ 的下标的集合仍为非空，则输出 $-1$ ，其他情况均可以构造出满足条件的 $01$ 间隔序列，最后注意把所有多出来的 $0$ 都单独放到一个序列作为答案。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <sstream>
using namespace std;
#define LL long long
const int maxn = 200000 + 100;
int len, cnt, Index, num;
bool flag;
vector<int> G[maxn];
set<int> st[2];
set<int>::iterator it;
char str[maxn];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%s", str + 1) != EOF) {
        cnt = 0;
        flag = true;
        len = strlen(str + 1);
        st[0].clear();
        st[1].clear();
        for(int i = 1; i <= len; ++i) {
            st[str[i] - '0'].insert(i);
        }
        while(!st[0].empty() && !st[1].empty()) {
            Index = 0;
            G[++cnt].clear();
            it = st[0].begin();
            while(it != st[0].end() && it != st[1].end()) {
                num = *it;
                G[cnt].push_back(num);
                st[Index].erase(it);
                Index = 1 - Index;
                it = st[Index].upper_bound(num);
            }
            if(str[G[cnt].back()] == '1') {
                flag = false;
                break;
            }
        }
        if(!st[1].empty() || !flag) {
            printf("-1\n");
            continue;
        }
        while(!st[0].empty()) {
            G[++cnt].clear();
            G[cnt].push_back(*st[0].begin());
            st[0].erase(st[0].begin());
        }
        printf("%d\n", cnt);
        for(int i = 1; i <= cnt; ++i) {
            len = G[i].size();
            printf("%d", len);
            for(int j = 0; j < len; ++j) {
                printf(" %d", G[i][j]);
            }
            printf("\n");
        }
    }
    return 0;
}

D. A Leapfrog in the Array

题意

最初有一个长度为 $2n-1$ 的数组，数组的每个偶数位都是空的，数组的 $2x-1$ 位上的数字为 $x$ ，然后将这个数组的最后一个数字放到数组的最后一个空着的位上，不断执行这个操作，直到数组中不再有空位为止，最终数组的长度为 $n$ ，对于一个长度为 $2n-1=7$ 的的初始数组，操作如下：

对于一个长度为 $n$ 的最终数组， $q$ 次询问它的第 $x$ 位上的数字的值。

输入

第一行为两个整数 $n,q~(1\leq n\leq10^{18},1\leq q\leq2\times10^5)$ ，接下去 $q$ 行每行一个整数 $x$ 。

输出

对于每次询问，输出最终数组 $x$ 位上的数字。

样例

输入	输出	提示
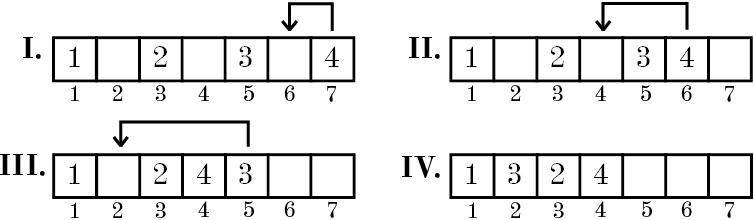
4 3 2 3 4	3 2 4	最终数组如上图所示。
13 4 10 5 4 8	13 3 8 9	最终数组为： $[1,12，2,8,3,11,4,9,5,13,6,10,7]$ 。

题解

对于每次询问，若 $x$ 为奇数，则答案为 $\frac{x+1}{2}$ ，否则将 $x$ 位上的数字还原到原来的位置上，第 $x$ 位上的数字，假设它左边所有的奇数位的数字都已经归位，偶数位上的数字都已经到它的后面，现在到这个位置上的数字还原，那么它左边的数字有 $\frac{x}{2}$ 个，右边的数字有 $n-\frac{x}{2}$ ，因此这个数字一次还原的位置为 $x+n-\frac{x}{2}$ ，不断还原下去，直到 $x$ 为奇数为止。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
LL n, q;
LL x, Index;
int main() {
    #ifdef LOCAL
        freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%I64d%I64d", &n, &q) != EOF) {
        while(q--) {
            scanf("%I64d", &x);
            while(x % 2 == 0) {
                x += n - x / 2;
            }
            printf("%I64d\n", (x + 1) / 2);
        }
    }
    return 0;
}

E. Data Center Maintenance

题意

有 $n$ 个银行， $m$ 个客户，每个客户都把自己的资料放在 $2$ 个银行，一天总共有 $h$ 小时，每个银行每天都要维护一小时，这一小时内银行无法工作，但是这一小时客户仍然可以在另一个银行提取资料，于是客户就可以一天 $h$ 小时随时提取资料。现在要选择 $k$ 个银行进行实验，每个进行实验的银行，它每天的维护时间都推迟一小时，如果原来的维护时间是 $h-1$ 时，进行实验后银行的维护时间就为 $0$ 时。问最少选择几个银行（至少一个）进行实验，才能仍然保证每一个客户随时都能提取到资料。

输入

第一行为 $3$ 个整数 $n,m,h~(2\leq n\leq10^5,1\leq m\leq10^5,2\leq h\leq10^5)$ ，第二行为 $n$ 个整数 $u_1,u_2,\cdots,u_n~(0\leq u_i<h)$ 表示第 $i$ 个银行一天内需要维护的时间点。接下去 $m$ 行每行两个整数 $c_{i,1},c_{i,2}~(1\leq c_{i,1},c_{i,2}\leq n)$ ，表示第 $i$ 个客户把资料存放在第 $c_{i,1}$ 和第 $c_{i,2}$ 个银行。数据保证最初每一个客户都可以在一天的任意时刻取得资料。

输出

第一行为一个整数 $k~(1\leq k\leq n)$ ，表示最少可以进行实验的银行数量，第二行为 $k$ 个整数 $x_1,x_2,\cdots,x_k~(1\leq x_i\leq n)$ ，表示 $k$ 个进行实验的银行编号，如果有多解，输出任意一个。

样例

输入	输出
3 3 5 4 4 0 1 3 3 2 3 1	1 3
4 5 4 2 1 0 3 4 3 3 2 1 2 1 4 1 3	4 1 2 3 4

题解

如果某个客户将他的资料放在两个维护时间相邻的银行，第一个银行的维护时间 $u_i$ 和第二个银行的维护时间 $u_j$ 的关系为 $(u_i+1)\%h=u_j$ ，那么第一个银行一旦进行实验，第二个银行也需要进行实验，否则两个银行的维护时间就会相同，于是我们将所有客户存放资料的两个银行，如果满足上面的条件，就从第一个银行连一条有向边到第二个银行，表示如果前一个银行开始了维护，那么后面的银行同时也需要进行维护。如果这张有向图是一个 $DAG$ ，那么只需要维护被指向的最后一个银行即可，如果有向图上存在环，就对有向图进行 $Tarjan$ 缩点成一个 $DAG$ ，然后找到出度为 $0$ 的点中点数最少的环。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
int n, m, h, v, u, ans_cnt;
int ans[maxn];
int num[maxn];
int top, bcnt, dcnt;
int sta[maxn], dfn[maxn], low[maxn], belong[maxn], deg[maxn];
bool ins[maxn];
int cnt[maxn];
vector<int> G[maxn];
vector<int> GG[maxn];
void dfs(int x) {
    dfn[x] = low[x] = ++dcnt;
    ins[x] = true;
    sta[top++] = x;
    int len = G[x].size();
    for(int i = 0; i < len; ++i) {
        int pos = G[x][i];
        if(dfn[pos] == 0) {
            dfs(pos);
            low[x] = min(low[x], low[pos]);
        } else if(ins[pos]) {
            low[x] = min(low[x], dfn[pos]);
        }
    }
    if(dfn[x] == low[x]) {
        ++bcnt;
        int pos;
        do {
            pos = sta[--top];
            ins[pos] = false;
            belong[pos] = bcnt;
            ++cnt[bcnt];
        } while(pos != x);
    }
}
void Tarjan() {
    bcnt = top = dcnt = 0;
    memset(cnt, 0, sizeof(cnt));
    memset(deg, 0, sizeof(deg));
    memset(dfn, 0, sizeof(dfn));
    memset(ins, 0, sizeof(ins));
    for(int i = 1; i <= n; ++i) {
        if(dfn[i] == 0) {
            dfs(i);
        }
    }
    for(int i = 1; i <= bcnt; ++i) {
        GG[i].clear();
    }
    for(int i = 1; i <= n; ++i) {
        int len = G[i].size();
        for(int j = 0; j < len; ++j) {
            int pos = G[i][j];
            int u = belong[i];
            int v = belong[pos];
            if(u != v) {
                GG[u].push_back(v);
                ++deg[u];
            }
        }
    }
}
int main() {
    #ifdef LOCAL
        freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d%d", &n, &m, &h) != EOF) {
        ans_cnt = 0;
        for(int i = 1; i <= n; ++i) {
            G[i].clear();
        }
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
        }
        for(int i = 0; i < m; ++i) {
            scanf("%d%d", &u, &v);
            if((num[u] + 1) % h == num[v]) {
                G[u].push_back(v);
            }
            if((num[v] + 1) % h == num[u]) {
                G[v].push_back(u);
            }
        }
        Tarjan();
        int Min = INT_MAX;
        int Index;
        for(int i = 1; i <= bcnt; ++i) {
            if(deg[i] == 0 && cnt[i] < Min) {
                Min = cnt[i];
                Index = i;
            }
        }
        for(int i = 1; i <= n; ++i) {
            if(belong[i] == Index) {
                ans[ans_cnt++] = i;
            }
        }
        printf("%d\n", ans_cnt);
        for(int i = 0; i < ans_cnt; ++i) {
            if(i != 0) {
                printf(" ");
            }
            printf("%d", ans[i]);
        }
        printf("\n");
    }
    return 0;
}

Codeforces Round #469 (Div. 2)

A. Left-handers, Right-handers and Ambidexters

题意

输入

输出

样例

题解

过题代码

B. Intercepted Message

题意

输入

输出

样例

题解

过题代码

C. Zebras

题意

输入

输出

样例

题解

过题代码

D. A Leapfrog in the Array

题意

输入

输出

样例

题解

过题代码

E. Data Center Maintenance

题意

输入

输出

样例

题解

过题代码

内容目录