@Dmaxiya 2020-12-12T07:24:04.000000Z 字数 6131 阅读 1332

Codeforces Round #495 (Div. 2)

Codeforces

Contests 链接：Codeforces Round #495 (Div. 2)
过题数：3
排名：844/5878

A. Sonya and Hotels

题意

如果在数轴上的某一个点与数轴上所有 $n$ 个点 $x_1,x_2,\cdots,x_n$ 的最小距离为 $d$ ，则这个点是合法的，问总共有多少个合法的点。

输入

输入第一行为两个整数 $n,d~(1\leq n\leq100,1\leq d\leq10^9)$ ，第二行为 $n$ 个整数 $x_1,x_2,\cdots,x_n~(-10^9\leq x_i\leq10^9)$ 。

输出

输出合法的点的数量。

样例

输入	输出	提示
4 3 -3 2 9 16	6	$6$ 个合法的点分别为 $−6,5,6,12,13,19$ 。
5 2 4 8 11 18 19	5	$5$ 个合法的点为 $2,6,13,16,21$ 。

题解

枚举 $2n$ 个点 $x_i\pm d$ ，对每个点判断是否合法，将点放到 $set$ 中去重，最终 $set$ 的大小就是答案。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100 + 100;
LL n, d;
LL x[maxn];
set<LL> st;
LL judge(LL Index) {
    LL ret = (1LL << 50);
    for(int i = 1; i <= n; ++i) {
        ret = min(ret, abs(x[i] - Index));
    }
    return ret;
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif //Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%I64d%I64d", &n, &d) != EOF) {
        st.clear();
        for(int i = 1; i <= n; ++i) {
            scanf("%I64d", &x[i]);
        }
        for(int i = 1; i <= n; ++i) {
            if(judge(x[i] - d) == d) {
                st.insert(x[i] - d);
            }
            if(judge(x[i] + d) == d) {
                st.insert(x[i] + d);
            }
        }
        printf("%d\n", (int)st.size());
    }
    return 0;
}

B. Sonya and Exhibition

题意

构造一个长度为 $n$ 的 $01$ 串，使得对于 $m$ 个闭区间 $[l_i,r_i]$ ， $\sum_{i=1}^mval_i$ 最大，其中 $val_i$ 表示区间 $[l_i,r_i]$ 内 $0$ 的数量乘上 $1$ 的数量的值。

输入

输入第一行为两个整数 $n,m~(1\leq n,m\leq10^3)$ ，接下去 $m$ 行每行两个整数 $l_i,r_i~(1\leq l_i\leq r_i\leq n)$ 。

输出

输出一个满足条件的 $01$ 串。

样例

输入	输出	提示
5 3 1 3 2 4 2 5	01100	$val_1=1\times2=2$ $val_2=2\times1=2$ $val_3=2\times2=4$ $\sum_{i=1}^3val_i=2+2+4=8$ 。
6 3 5 6 1 4 4 6	110010	$val_1=1\times1=1$ $val_2=2\times2=4$ $val_3=1\times2=2$ $\sum_{i=1}^3val_i=1+4+2=7$ 。

题解

由固定周长面积最大的四边形是正方形可知，在区间长度为 $len$ 的区间内， $0$ 的数量和 $1$ 的数量越接近，它们的乘积就越大，只要输出 $01$ 相间的 $01$ 串就能满足条件，如果有多解输出任意一个。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 1000 + 100;
struct Node {
    int l, r;
};
bool operator<(const Node &a, const Node &b) {
    return (a.r == b.r? a.l > b.l: a.r < b.r);
}
int n, m;
int cnt[2];
Node node[maxn];
char ans[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif //Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &m) != EOF) {
        for(int i = 1; i <= m; ++i) {
            scanf("%d%d", &node[i].l, &node[i].r);
        }
        for(int i = 0; i < n; ++i) {
            if(i % 2 == 0) {
                putchar('1');
            } else {
                putchar('0');
            }
        }
        printf("\n");
    }
    return 0;
}

C. Sonya and Robots

题意

有两个机器人在一排 $n$ 个数字 $a_1,a_2,\cdots,a_n$ 的两端，只要分别给两个机器人一个数字指令，在左边的机器人就会往右边走，直到走到数字指令 $p$ 所在的位置停止，在右边的机器人将往左边走，直到走到数字指令 $q$ 所在的位置停止，在保证两个机器人不相撞的情况下，有多少种合法的数字指令 $p_i,q_i$ 是满足条件的，两个数字指令是不同的，当且仅当 $p_i\neq p_j$ 或者 $q_i\neq q_j$ 。

输入

输入第一行为一个整数 $n~(1\leq n\leq10^5)$ ，第二行为 $n$ 个整数 $a_1,a_2,\cdots,a_n~(1\leq a_i\leq10^5)$ 。

输出

输出所有合法的数字指令数。

样例

输入	输出	提示
5 1 5 4 1 3	9	这些数字指令都是合法的： $(1,1),(1,3),(1,4),(1,5),(4,1),(4,3),(5,1),(5,3),$ $(5,4)$ 。
7 1 2 1 1 1 3 2	7	这些数字指令是合法的： $(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,2)$ 。

题解

统计每一个数字出现的最左边的下标和最右边的下标，对于每一个出现的数字（不能重复统计），计算有多少个数字出现的最右边的下标在这个数字出现的最左边的下标的右边，对每个数字 $O(\log n)$ 地二分查找，就可以 $O(n\log n)$ 地解决问题了。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
struct Node {
    int Index, num;
    Node() {}
    Node(int I, int n) {
        Index = I;
        num = n;
    }
};
bool operator<(const Node &a, const Node &b) {
    return a.Index < b.Index;
}
LL ans;
int n, cnt;
int num[maxn], Left[maxn], Right[maxn];
Node node[maxn];
Node *it;
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif //Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        ans = 0;
        cnt = 0;
        memset(Right, 0, sizeof(Right));
        memset(Left, 0x3f, sizeof(Left));
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
            Left[num[i]] = min(Left[num[i]], i);
            Right[num[i]] = max(Right[num[i]], i);
        }
        for(int i = 1; i < maxn; ++i) {
            if(Right[i] != 0) {
                node[cnt++] = Node(Right[i], i);
            }
        }
        sort(node, node + cnt);
        for(int i = 1; i < maxn; ++i) {
            if(Right[i] != 0) {
                it = upper_bound(node, node + cnt, Node(Left[i], i));
                ans += cnt - (it - node);
            }
        }
        printf("%I64d\n", ans);
    }
    return 0;
}

D. Sonya and Matrix

题意

在一个 $n\times m$ 的网格内，从上到下、从左到右将每个点的坐标设为 $(x_i,y_i)$ ，在网格中选择一个点 $(x,y)$ ，然后将网格上所有位置都填上数字 $|x-x_i|+|y-y_i|$ ，这样将所有相同的数字连起来，就是一个个嵌套起来的菱形。现在给出 $t$ 个整数 $a_1,a_2,\cdots,a_t$ ，判断这些数字能否填入上述网格内。

输入

第一行为一个整数 $t~(1\leq t\leq10^6)$ ，第二行为 $t$ 个整数 $a_1,a_2,\cdots,a_t~(0\leq a_i<t)$ 。

输出

如果无法满足题意，则输出 $-1$ ，否则第一行输出两个整数 $n,m$ ，表示构造出来的网格大小，第二行为两个整数 $x,y$ ，表示在网格中数字 $0$ 的坐标，如果有多解输出任意一个。

样例

输入	输出	提示
20 1 0 2 3 5 3 2 1 3 2 3 1 4 2 1 4 2 3 2 4	4 5 2 2	数字可以按照下图填入 $4\tim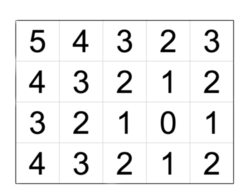es 5$ 的网格中也可以将网格旋转 $k\times90°$ ，将 $0$ 放到 $(2,2)~(2,3)~(4,2)$ 等位置。
18 2 2 3 2 4 3 3 3 0 2 4 2 1 3 2 1 1 1	3 6 2 3
6 2 1 0 2 1 2	-1

题解

首先如果整个网格是无穷大的，那么除了 $0$ 以外，每个数字 $x$ 出现的次数应该为 $4X$ ，因此可以通过这个来判断最先被截断的数字是什么，若最先被截断的数字等于 $x$ ，则数字 $0$ 一定被放在第 $x$ 行，其次可以发现，无论如何从无穷大的网格中截出一个 $n\times m$ 的网格，网格的四个角落中一定有一个是 $n\times m$ 个数字中的最大值，可以将这个值放在网格的右下角，这样就可以直接算出 $0$ 的坐标，确定了 $0$ 的坐标，就可以 $O(nm)$ 地确定是否每个数都能放在网格中，而 $n,m$ 可以通过枚举 $t$ 的因子确定。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 1000000 + 100;
int t, x, Max;
int cnt[maxn], cnttmp[maxn];
bool judge(int n, int m, int x, int y) {
    memcpy(cnttmp, cnt, sizeof(cnt));
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= m; ++j) {
            int dis = abs(i - x) + abs(j - y);
            --cnttmp[dis];
            if(cnttmp[dis] < 0) {
                return false;
            }
        }
    }
    return true;
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif //Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d", &t) != EOF) {
        bool flag = false;
        Max = 0;
        memset(cnt, 0, sizeof(cnt));
        for(int i = 0; i < t; ++i) {
            scanf("%d", &x);
            ++cnt[x];
            Max = max(Max, x);
        }
        if(t == 1) {
            if(Max == 0) {
                printf("1 1\n1 1\n");
            } else {
                printf("-1\n");
            }
            continue;
        }
        int x, y, n, m;
        for(int i = 1; i < maxn; ++i) {
            if(cnt[i] != i * 4) {
                x = i;
                break;
            }
        }
        for(int i = 1; i <= t / i; ++i) {
            if(t % i == 0) {
                n = i;
                m = t / i;
                y = n - x + m - Max;
                if(judge(n, m, x, y)) {
                    flag = true;
                    break;
                }
                n = t / i;
                m = i;
                if(judge(n, m, x, y)) {
                    flag = true;
                    break;
                }
            }
        }
        if(flag) {
            printf("%d %d\n%d %d\n", n, m, x, y);
        } else {
            printf("-1\n");
        }
    }
    return 0;
}

Codeforces Round #495 (Div. 2)

A. Sonya and Hotels

题意

输入

输出

样例

题解

过题代码

B. Sonya and Exhibition

题意

输入

输出

样例

题解

过题代码

C. Sonya and Robots

题意

输入

输出

样例

题解

过题代码

D. Sonya and Matrix

题意

输入

输出

样例

题解

过题代码

内容目录