Codeforces Round #453 (Div. 2)

Codeforces

Contests 链接：Codeforces Round #453 (Div. 2)
过题数：3
排名：408/8956

A. Visiting a Friend

题意

$Pig$ 的家在 $x=0$ 处，他的朋友家在 $x=m$ 处，他将要拜访这位朋友，在路上有 $n$ 个传送点，每个传送点的位置是 $x=a_i$，每个传送点都有一个最远能够传送到的最右边的位置 $b_i$，它可以将 $Pig$ 从 $a_i$ 传送到 $[a_i,b_i]$ 之间的任意一点，问 $Pig$ 是否可以只通过传送点就到达他的朋友家。

输入

第一行为两个整数 $n,m~(1\leq n,m\leq100)$，接下去 $n$ 行每行两个整数 $a_i,b_i~(0\leq a_i\leq b_i\leq m)$，对于每一个 $2\leq i\leq n$，都满足 $a_i\geq a_{i-1}$。

输出

如果 $Pig$ 可以只通过传送点就到达他的朋友家，输出 $YES$，否则输出 $NO$，大小写任意。

样例

输入	输出	提示
3 5 0 2 2 4 3 5	YES	如图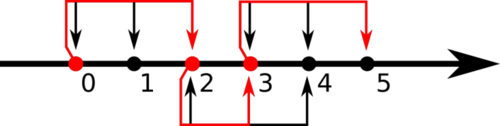： $Pig$ 可以从 $0$ 到达 $2$，然后通过第二个传送点到达 $3$，再通过第三个传送点到达 $5$。
3 7 0 4 2 5 6 7	NO	如图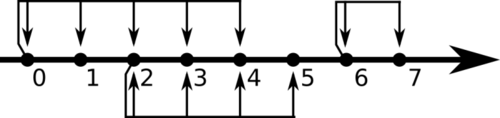： $Pig$ 无法从 $0$ 通过传送点到达他的朋友家。

题解

按照题意模拟，从 $0$ 开始，尽量往远处跑，最后能够跑到的点只要大于等于 $m$，就输出 $YES$。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
#define LL long long
int n, m, a, b, ans;
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &m) != EOF) {
        ans = 0;
        for(int i = 0; i < n; ++i) {
            scanf("%d%d", &a, &b);
            if(ans >= a) {
                ans = max(ans, b);
            }
        }
        if(ans >= m) {
            printf("YES\n");
        } else {
            printf("NO\n");
        }
    }
    return 0;
}

B. Coloring a Tree

题意

对于一棵 $n$ 个节点的有根树，给这棵树上的每个节点都涂上一种颜色，每次涂色可以选择一个节点，并将这个节点的子树（包括这个节点自身）全都涂上这种颜色，每个节点初始的颜色都是 $0$，要按照给定的涂色方式将这棵树涂上颜色，问最少需要涂多少次颜色。

输入

第一行为一个整数 $n~(2\leq n\leq10^4)$，第二行为 $n-1$ 个整数 $p_2,p_3,\cdots,p_n~(1\leq p_i<i)$，第 $i$ 个整数 $p_i$ 代表第 $i$ 个节点的父节点，第三行为 $n$ 个整数 $c_1,c_2,\cdots,c_n~(1\leq c_i\leq n)$，表示每个节点要涂上的颜色。

输出

输出最少需要涂色的次数。

样例

输入	输出	提示
6 1 2 2 1 5 2 1 1 1 1 1	3	给定的树如图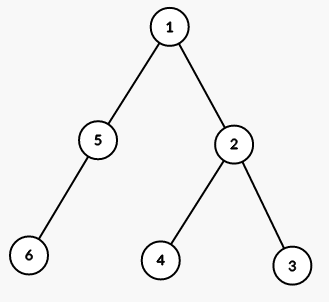： 首先选择树根并将整棵树涂成颜色 $2$，如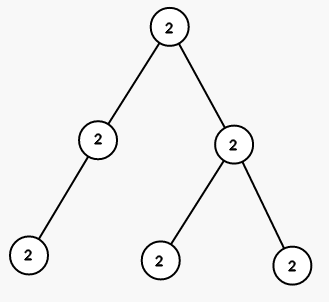图： 接着可以选择节点 $5$ 并将 $5$ 的子树都涂成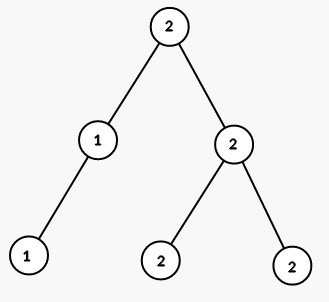颜色 $1$： 最后选择节点 $2$ 并将对应的子树都涂成颜色 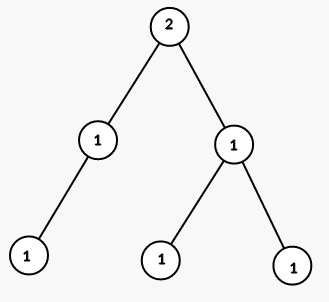$1$：
7 1 1 2 3 1 4 3 3 1 1 1 2 3	5

题解

贪心地从根节点开始涂色，按照 $dfs$ 的顺序先涂根节点，再涂它的子树，只有出现子节点颜色和父节点颜色不同的时候才需要涂色，因此只要统计子节点颜色和父节点颜色不同的个数就是答案。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 10000 + 100;
int n, ans;
int color[maxn], fa[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        ans = 0;
        for(int i = 2; i <= n; ++i) {
            scanf("%d", &fa[i]);
        }
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &color[i]);
            if(color[i] != color[fa[i]]) {
                ++ans;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

C. Hashing Trees

题意

给定一个长度为 $h+1$ 的序列 $a_0,a_1\cdots,a_h$，第 $i$ 个数字 $a_i$ 表示一棵树上第 $i$ 层的节点数为 $a_i$，判断是否存在不同构的满足条件的两棵树。

输入

第一行为一个整数 $h~(2\leq h\leq10^5)$，第二行为 $h+1$ 个整数 $a_0,a-1,\cdots,a_h~(1\leq a_i\leq2\times10^5)$，数据保证至少有一种满足条件的树的结构，且 $\sum_{i=0}^ha_i\leq2\times10^5$。

输出

如果只有唯一一种满足条件的树的结构，则输出 $perfect$，否则在第一行输出 $ambiguous$，接下来两行每行 $\sum_{i=0}^ha_i$ 个数字，第 $i$ 个数字表示第 $i$ 个节点的父节点，如果这个节点为根节点，则它的父节点为 $0$。

样例

输入	输出	提示
2 1 1 1	perfect	给定的序列只有唯一一种满足条件的树的结构：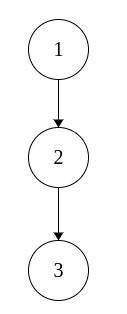
2 1 2 2	ambiguous 0 1 1 3 3 0 1 1 3 2	给定的序列有两种满足条件的结构：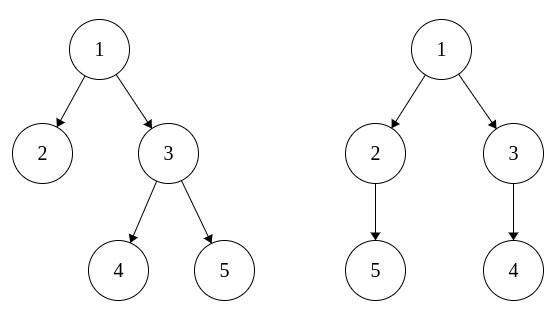

题解

序列中只要存在两个连续的大于等于 $2$ 的数字，就存在两种不同构的树满足条件，第一棵数每一层都以上一层的第一个节点为父节点，第二棵树只要在连续的两个 $2$ 中第二个 $2$ 对应的那一层，拿出一个节点作为上一层第二个节点的子节点，两棵树就不是同构的了。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn = 200000 + 100;
int h, cnt;
int num[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d", &h) != EOF) {
        int Index = -1;
        cnt = 1;
        for(int i = 0; i <= h; ++i) {
            scanf("%d", &num[i]);
        }
        for(int i = 0; i < h; ++i) {
            if(num[i] >= 2 && num[i + 1] >= 2) {
                Index = i + 1;
                break;
            }
        }
        if(Index == -1) {
            printf("perfect\n");
            continue;
        }
        printf("ambiguous\n");
        int root = 0;
        int first = 0;
        for(int i = 0; i <= h; ++i) {
            root = first;
            first = cnt;
            for(int j = 0; j < num[i]; ++j) {
                if(i != 0) {
                    printf(" ");
                }
                printf("%d", root);
                ++cnt;
            }
        }
        printf("\n");
        cnt = 1;
        first = 0;
        for(int i = 0; i <= h; ++i) {
            root = first;
            first = cnt;
            for(int j = 0; j < num[i]; ++j) {
                if(i != 0) {
                    printf(" ");
                }
                if(Index == i && j == 1) {
                    printf("%d", root + 1);
                } else {
                    printf("%d", root);
                }
                ++cnt;
            }
        }
        printf("\n");
    }
    return 0;
}