@Dmaxiya
2018-08-17T02:14:45.000000Z
字数 3174
阅读 1320
Codeforces Round #475 (Div. 1)
Codeforces
Contests 链接:Codeforces Round #475 (Div. 1)
过题数:2
排名:306/1883
A. Alternating Sum
题意
给定 的值,以及 项系数 ,所有系数不是 就是 ,这 项系数是以 为循环节的,且 ,给定前 项系数,求公式 的值。
输入
第一行为 个整数 ,第二行包含一个长度为 的字符串,字符串只包含
+和-这两种字符,表示系数的正负。
输出
输出计算结果。
样例
| 输入 |
|---|
2 2 3 3+-+ |
| 输出 |
| 7 |
| 提示 |
| 。 |
| 输入 |
|---|
4 1 5 1- |
| 输出 |
| 999999228 |
| 提示 |
| 。 |
题解
只观察每 个数字,会发现这这些项是以 为公比的等差数列,套上等比数列求和公式就可以得到答案,注意公比为 的情况。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <climits>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <functional>#include <algorithm>using namespace std;#define LL long longconst LL MOD = 1000000009;const int maxn = 100000 + 100;LL n, a, b, k;char str[maxn];LL fast_pow(LL res, LL n) {LL ans;for(ans = 1; n != 0; n >>= 1) {if(n % 2 == 1) {ans = (ans * res) % MOD;}res = (res * res) % MOD;}return ans;}void exgcd(LL a, LL b, LL &x, LL &y) {if(b == 0) {x = 1;y = 0;return ;}exgcd(b, a % b, y, x);y -= x * (a / b);}LL inv(LL x) {LL xx, yy;exgcd(x, MOD, xx, yy);xx = ((xx % MOD) + MOD) % MOD;return xx;}int main() {#ifdef LOCALfreopen("test.txt", "r", stdin);#endif // LOCALwhile(scanf("%I64d%I64d%I64d%I64d", &n, &a, &b, &k) != EOF) {if(k >= n + 1) {k = n + 1;}scanf("%s", str);LL tmp = 0;LL inva = inv(a);LL invb = inv(b);LL aa = fast_pow(a, n + 1);LL bb = invb;for(LL i = 0; i < k; ++i) {aa = (aa * inva) % MOD;bb = (bb * b) % MOD;if(str[i] == '+') {tmp += (aa * bb) % MOD;} else {tmp -= (aa * bb) % MOD;}tmp = ((tmp % MOD) + MOD) % MOD;}LL q = fast_pow((inva * b) % MOD, k);LL nn = (n + 1) / k;if(q == 1) {tmp = (nn * tmp) % MOD;} else {LL fenzi = (((1 - fast_pow(q, nn)) % MOD) + MOD) % MOD;LL fenmu = ((1 - q) % MOD + MOD) % MOD;fenzi = (fenzi * inv(fenmu)) % MOD;tmp = (tmp * fenzi) % MOD;}printf("%I64d\n", tmp);}return 0;}
B. Destruction of a Tree
题意
给定一个 个节点的树,每次可以从树上选择一个度为偶数的节点进行删除,每删除一个节点,与这个节点相连的所有边都被删除,问能否删除整棵树。
输入
第一行为一个整数 ,第二行为 个整数 ,如果 ,表示节点 和 之间有一条连边,数据保证给定的结构是一棵树。
输出
如果无法删除整棵树,输出 ,否则在第一行输出 ,接下去 行输出 个整数,表示删除节点的顺序。
样例
| 输入 |
|---|
| 5 0 1 2 1 2 |
| 输出 |
| YES 1 2 3 5 4 |
| 提示 |
删点过程如下: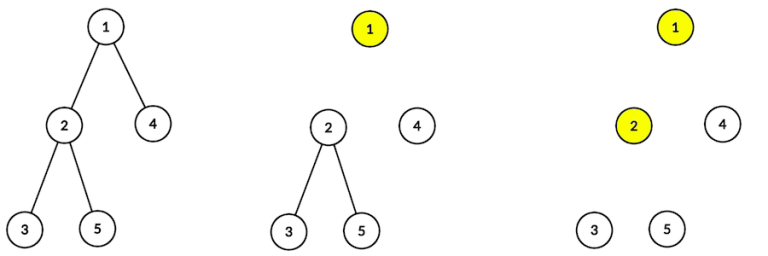 |
| 输入 |
|---|
| 4 0 1 2 3 |
| 输出 |
| NO |
题解
从叶子节点往树根 ,只要发现某个节点的度为偶数,就立即删除这个节点并往下 ,最后注意剪枝。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <climits>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <functional>#include <algorithm>using namespace std;#define LL long longconst int maxn = 200000 + 100;int n, p, cnt;int ans[maxn], deg[maxn];bool vis[maxn];vector<int> G[maxn];queue<int> que;void dfs(int f, int x, bool flag) {int len = G[x].size();if(!flag) {for(int i = 0; i < len; ++i) {int pos = G[x][i];if(!vis[pos] && pos != f) {dfs(x, pos, false);}}}if(deg[x] % 2 == 0) {deg[x] = 0;ans[cnt++] = x;vis[x] = true;for(int i = 0; i < len; ++i) {int pos = G[x][i];if(!vis[pos]) {--deg[pos];if(pos != f) {dfs(x, pos, true);}}}}}int main() {#ifdef LOCALfreopen("test.txt", "r", stdin);#endif // LOCALwhile(scanf("%d", &n) != EOF) {cnt = 0;for(int i = 1; i <= n; ++i) {G[i].clear();deg[i] = 0;vis[i] = false;}for(int i = 1; i <= n; ++i) {scanf("%d", &p);if(p != 0) {G[i].push_back(p);G[p].push_back(i);++deg[i];++deg[p];}}dfs(1, 1, false);if(cnt != n) {printf("NO\n");continue;}printf("YES\n");for(int i = 0; i < cnt; ++i) {printf("%d\n", ans[i]);}}return 0;}
