数学与算法竞赛

数学与生活

—— 2014210967 官展鹏

---

　　算法竞赛要求选手在规定时间内对给定的题目设计解决问题的算法并编程实现。这些问题涉及的方面非常广泛，有动态规划、搜索、贪心、字符串、母函数、模拟、图论……而数学知识也是题目可能涉及的知识点，在数学方面的知识要求有离散数学、组合数学、数论等，本篇论文将从数学在优化算法时间复杂度与取模运算中的应用两个方面讨论数学在算法竞赛中的应用，最后以一个组合计数问题具体体现数学在其中发挥的作用。

算法竞赛的限制

　　算法竞赛对于比赛选手给出的算法，既要求算法运行对于一定规模的数据能够快速地得到答案，也要求执行算法占用的空间不能太大，因此算法竞赛的题目有严格的时间和空间上的限制。

时间限制

　　大多数问题要求程序在 $1s$ 的时间内得到答案，如果得到答案的时间超出了题目给定的时间限制，则选手的代码将会被判定为超时，该题无法通过。
　　具体而言，计算机每秒能够执行的计算次数约为 $10^8$，因此我们可以用算法解决问题所需要执行的次数进行大致的估算，与 $10^8$ 进行比较，从而判断自己的算法能否通过该题。

空间限制

　　大多数情况下，每个问题对空间的限制为 $256M$，大约允许计算机开辟 $6.4\times10^7$ 个单元大小的空间（以 $4$ 字节为一个单元大小进行估算），如果程序申请的空间大小超过这个值，则选手的代码将会被判定为内存超限，该题无法通过。

数据范围限制

　　这一限制属于选手选择编程语言自身的限制，计算机用 $2$ 进制数来储存十进制数，一个 $8$ 位的有符号 $2$ 进制数能够储存 $-128$ 到 $127$ 之间总共 $256$ 个整数，在 C/C++ 以及 Java 语言的基本数据类型中，精度最高的能够表示的十进制数是由 $64$ 位有符号 $2$ 进制数表示的，该类型能够表示的数据范围大致为 $[-9\times10^{18},9\times10^{18}]$，而如果问题的求解答案超出了这个范围计算时就会出现溢出错误，这时候就需要用到特殊的数据类型（Java 可以用 BigInteger 类，而 python 没有该限制，本篇论文只讨论整数数据类型的计算，不讨论实数的计算）。

复杂度分析

　　由于问题存在时间限制与空间限制（数据范围限制将在“数学在取模运算中的应用”部分讨论），因此减少算法的求解时间与内存占用就成了在提出算法后最主要的问题，在提出算法优化之前，先对算法的时间复杂度与空间复杂度进行一些了解。

时间复杂度

　　上面提到，计算机的计算速度大约为 $10^8$ 次$/s$，因此可以用程序需要执行的次数来估计执行时间，算法的执行次数一定与问题的规模成比例。
　　例如要对 $1$ 到 $n$ 之间（包括 $1$ 与 $n$）所有的自然数进行求和，如果让程序计算公式 $1+2+3+\cdots+n$，那么计算机就需要执行 $n$ 次加法，因此这种算法的执行次数随着 $n$ 的变化而线性变化，我们可以估计这种算法的时间复杂度为 $O(n)$，而如果应用求和公式 $\frac{(1+n)\times n}{2}$，那么就只需要计算一次加法、一次乘法和一次除法，计算机总共需要执行 $3$ 次运算，而这种算法的执行次数并不随着 $n$ 的变化而变化，我们将 $3$ 视为常数，忽略计算次数中的常数，可以认为这个算法的时间复杂度就是 $O(1)$ 的。分别用两种算法解决同一个问题，第一个算法在问题规模达到 $n=10^8$ 时就已经到达上限，而第二种算法可以在 $n\in[1,10^9]$ 内立即得到正确结果（当 $n$ 取更大值时可能会出现计算过程溢出错误）。
　　如果我们让计算机执行 $1+1+2+2+3+3+\cdots+n+n$，每个数字都加了两次，那么总共的执行加法次数是 $2n$，算法的执行次数也是随着 $n$ 的变化而线性变化，我们将前面的常数 $2$ 忽略（因为 $2$ 并不随着 $n$ 的变化而变化），因此这一算法的时间复杂度也为 $O(n)$。
　　再比如对于一个单调连续函数 $f(x)$，如果函数满足条件 $f(a)f(b)<0$，由零点存在性定理与函数单调性可知，在区间 $(a,b)$ 内一定存在一个零点，那么我们可以用二分的方法无限逼近这个零点，而二分的次数与 $a$ 和 $b$ 的值以及目标精度有关，假设目标精度为一个非常小的小数 $eps$，那么二分需要执行的次数为 $\log_2\frac{b-a}{eps}$，如果令 $eps=1$ 且 $b-a=n$，那么二分的次数就为 $\log_2n$，我们可以估计这个算法的时间复杂度为 $O(\log_2n)$（尽管这种对 $eps$ 的赋值方式看起来会导致非常大的精度误差，但是在零点一定为整数点的情况下，可以认为如此二分就可以得到正确答案，而在实际只涉及到整数解的题目中，这一点也一定是成立的）。

空间复杂度

　　与时间复杂度相同，空间复杂度也用一个关于问题规模 $n$ 的表达式进行估计。
　　例如在数学中，我们习惯用邻接矩阵来表示一张图，矩阵的第 $i$ 行第 $j$ 列的数字表示节点 $i$ 到节点 $j$ 之间的路径长度，如果一张图有 $n$ 个节点，那么邻接矩阵的大小就需要 $n^2$，我们可以说邻接矩阵对图储存信息的方式所需要的空间复杂度为 $O(n^2)$，由于算法竞赛的一般内存限制，用邻接矩阵来储存图的节点与边的信息最多只能存下 $3000$ 个节点的图。
　　对于边比较多的稠密图而言邻接矩阵在边的信息的存取方面都有很高的效率，而往往很多情况下的图不一定任意两个节点之间都有连边，节点越多的图节点之间的边可能就越稀疏，因此如果用邻接矩阵将会有许多位置都储存了数字 $0$ 或者 $\infty$，造成了大量的空间浪费。在数据结构中有一种高效的存图结构：邻接链表，这种存图数据结构的空间复杂度为 $O(m)$，其中 $m$ 为图上边的数量，因此图上有多少条边，就只需要多少的空间，极大地利用了空间，并且由于这种数据结构不会储存不存在的边的信息，访问一个节点相邻边的速度在稀疏图中远远高于邻接矩阵，因此它在各种算法中得到广泛应用。

由于时间 / 空间复杂度描述的是在问题规模扩大的情况下，解决问题所需要的时间、空间随着问题规模增长的情况，因此我们不必精确计算每种算法具体需要多少字节、多少次计算，只需要估算出一个大概的值即可，因此我们经常忽略常数的估算，而只用与题目给出的数据有关的表达式进行描述，常用的表达式有：$O(n!),O(k^n),O(n^k),O(n),O(\sqrt n),O(\log n),O(1)$ 以及它们的乘积如 $O(n\log n)$ 等，这些将在后面的计算中具体提到。
注意：

1. 其中 $k$ 通常是值为 $2$ 或者 $3$ 的常数，由于 $k^n$ 与 $n^k$ 中 $k$ 的大小对计算得到的数值有数量级上的影响，因此不能忽略。
2. 由于在算法中经常有二分或者与 $2$ 的次幂有关的运算，时间复杂度涉及到 $O(\log_an)$ 的经常是以 $2$ 为底数，因此在后面的书写中 $\log n$ 在忽略底数的情况下默认等于 $\log_2n$。

数学在时间复杂度优化方面的应用

　　显然在数学中一个公式的化简能大大提高算法执行的效率，这种优化将是数量级上的优化，且一些定理的证明也能大大改善算法的时间复杂度。在讨论时间复杂度时的等差数列求和公式就是一个很好的例子。这里从“俄罗斯农民乘法”到“快速幂”以及对常见的斐波那契数列的应用，来从另一方面说明数学在算法时间复杂度优化方面的作用。

俄罗斯农民乘法

　　在计算 $a\times b$ 时，假设计算机只能做加法运算而无法做乘法运算，我们应如何快速得到这个结果呢？
　　最慢的方式就是做 $\min(a,b)$ 次加法一个一个数字地加，这种算法的时间复杂度为 $O(n)$，其中 $n=\min(a,b)$。
　　从计算机的二进制表示数可以得到启发：两个 $a$ 相加的结果是 $2a$，而如果继续将这个数字对自身做加法就能得到 $4a$，这样的计算增长的速度是 $2^n$ 指数级的，因此可以很快得到 $a,2a,4a,\cdots,2^na$ 的结果，将这些系数凑出系数 $b$ 并将相应系数对应的结果相加，就能得到 $a\times b$ 的值，凑系数的过程相当于将一个 $10$ 进制数 $b$ 表示成一个 $2$ 进制数的过程，这个转化过程在谭浩强的《C语言程序设计》或者《数字逻辑》、《电子技术基础》等必修课书目中已经做过具体分析，这里不再展开。
　　值得注意的是，这种算法的时间复杂度，由于 $a$ 的系数的增长是 $2^n$ 级的，而计算到 $2^n$ 需要的计算次数为 $n$，为凑出整数 $b$，也应该满足 $2^n\leq b<2^{n+1}$，因此总的时间复杂度为 $O(\log b)$，如果要计算的是 $a\times n$ 的结果，时间复杂度就是 $O(\log n)$（实际上只是一个变量名的区别）。

快速幂

　　$a\times b$ 是 $b$ 个 $a$ 相加的结果，其中乘法是多个相同数字加法的快速运算，类似地，幂运算是多个相同数字乘法的快速运算，在求 $a^n$ 时，我们也可以用同样的方法，在 $O(\log n)$ 的时间复杂度内求解问题。
　　显然这样的问题背景比俄罗斯农民乘法的问题背景更容易给出，或者说快速幂在算法竞赛中对解决问题更有实际意义，因此快速幂运算在算法竞赛中更经常碰到，而俄罗斯农民乘法仅在部分特殊情况下才会被用到，实际上它们两种算法的原理是一样的，俄罗斯农民乘法的实际背景将在“数学在取模运算中的应用”部分做简要说明。

矩阵快速幂

　　应用快速幂 / 俄罗斯农民乘法，其中隐含的一个重要的性质，就是乘法和加法都满足结合律（交换律在其中并没有被应用到），因此我们可以将这种算法的对象进一步推广：只要某种运算满足结合律，该运算的多次重复计算就可以应用该算法进行优化。由于矩阵乘法也满足结合律，因此该算法也适用于矩阵的幂运算（虽然矩阵加法同样满足结合律，但是矩阵的乘法运算比加法运算有更普遍的意义及应用，因此这里不对矩阵加法进行讨论，它们具有相同的原理）。

斐波那契数列

　　斐波那契数列是我们所熟知的数列，其中有许多非常神奇的性质，如黄金分割比、相邻项互质等，这里我们关心的是如何快速求解斐波那契数列的第 $n$ 项。
　　斐波那契数列的通项公式为：

$$fib_n=\begin{cases} 1&n=1,2\\ fib_{n-1}+fib_{n-2}&n>2 \end{cases}$$
　　从这个递推式我们可以很容易写出一个与递推式相关的矩阵：
$$\begin{pmatrix} fib_n\\fib_{n-1} \end{pmatrix} =\begin{pmatrix} 1&1\\1&0 \end{pmatrix} \begin{pmatrix} fib_{n-1}\\fib_{n-2} \end{pmatrix}$$
将 $\begin{pmatrix}fib_{n-1}\\fib_{n-2}\end{pmatrix}$ 展开直到数列的第 $1$ 项可以得到：
$$\begin{pmatrix} fib_n\\fib_{n-1} \end{pmatrix} =\begin{pmatrix} 1&1\\1&0 \end{pmatrix}^{n-2} \begin{pmatrix} fib_2\\fib_1 \end{pmatrix}$$
其中 $\begin{pmatrix}1&1\\1&0\end{pmatrix}^{n-2}$ 就可以用矩阵快速幂来 $O(\log n)$ 地求解得到，因此原本只能通过递推式 $O(n)$ 地计算到第 $10^8$ 项，现在可以利用矩阵快速幂计算到第 $2^{10^8}$ 项（理论上如此）。

这里仅对快速乘与快速幂及其应用做具体讨论，实际上数学方法在算法优化上的作用不仅限于此，如二项式公式的应用，在组合计数问题中对最终得到的公式的化简，母函数的应用、欧拉函数的应用等，这里不一一详述。

数学在取模运算中的应用

　　由于计算机的基本数据类型所能表示的范围有限，对更高位数值的计算需要借助其他类，高精度计算一方面会消耗大量的内存，另一方面随着位数的增加，数值的计算速度会越来越慢，且一般情况下我们只关心算法能否在限定时间内得到正确结果，更高精度的计算除了徒增运行时间，在算法方面的考察并没有太大的作用，如果我们有一种方法能够将一个高精度数在计算机基本数据类型能够表达的数据范围内找到一个映射值，那么我们就可以通过比较映射的结果是否相等来判定算法执行的结果是否正确。
　　如果这个映射出现冲突的概率太大，使多个高精度数映射为同一个数字，对计算结果的检验将十分不利，因此算法问题中经常采取对一个大质数 $p$ 取余（取模）的运算来将一个高精度数映射为 $0$ 到 $p-1$ 之间的数字，$p$ 的数量级一般在 $10^7$ 或者 $10^9$。
　　为了保证原高精度数计算后对 $p$ 取模的结果与高精度数对 $p$ 取模后的数字之间做计算能够得到相同的结果，我们需要一些辅助的取模公式，最基本的有：

加减法：
加法：$\quad\quad(a+b)\%p=(a\%p+b\%p)\%p$
若 $b<0$：$\quad b=>（b\%p+p）\%p$
减法：$\quad\quad((a-b)\%p+p)\%p=((a\%p–b)\%p+p)\%p$

乘除法：
乘法：$\quad(a\times b)\%p=((a\%p)\times(b\%p))\%p$
逆元：$\quad$ 若 $(a\times b)\%p=1$，则 $b$ 是 $a$ 相对于 $p$ 的逆元，记为 $a^{-1}=b\quad(\mod p)$
除法：$\quad (a\div b)\%p=((a\%p)\times b^{-1})\%p$

　　现在我们可以提出俄罗斯农民乘法的应用背景了：如果我们需要计算 $(a\times b)\%p$ 的结果，而 $p^2>9\times10^{18},2p<9\times10^{18}$ 时，$(a\%p)\times(b\%p)$ 的计算将会出现溢出错误，无法得到正确的结果，而加法计算不会出现溢出错误，因此计算机只能进行加法计算，此时就可以应用俄罗斯农民乘法对问题进行求解。
　　其中的最后一点，在取模运算中进行除法，没有具体说明如何求解 $b$ 的逆元，这一部分涉及到一些数论知识，本文中没有提及，如果对此有兴趣，具体的证明推导过程可以前往欧拉函数相关数论及文中相关链接查看。

例题详解

　　前面提到的许多应用，都是属于“知识型”内容，可能无法切实体会到数学在算法竞赛中的应用，这里以一道组合计数问题 Sky Full of Stars 为例，通过体会算法题的推导求解过程，来感受数学在其中担任的重要角色。

题意

在一个 $n\times n$ 的网格中，可以给每一格方格填充红、绿、蓝中的一种颜色，则总共有 $3^{n \times n}$ 种涂色方案，问在这些方案中，至少有一行或者一列颜色相同的涂色方案数。

输入

输入只包含一个整数 $n~(1\leq n\leq10^6)$。

输出

输出所有合法的涂色方案数对 $998244353$ 取模的结果。

样例

输入	输出	提示
1	3	由于只有一行一列，因此所有涂色方案都是合法的，总共有 $3^1=3$ 种涂色方案。
2	63	当 $n=2$ 时，以下两种涂色方案是合法的： 而以下两种涂色方案是不合法的：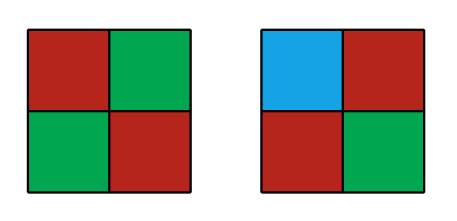
3	9933

题解

首先计算某几行以及某几列颜色相同的情况，如：

$$\begin{matrix} BRG&GBB\\ GGG&GBB\\ GRB&RBB\\ \end{matrix}$$
在这些情况中，颜色相同的所有行和列都为同一种颜色的情况会被重复计算如：
$$\begin{matrix} GGG&RRR\\ RBG&RBG\\ RGG&RRR \end{matrix}$$
这些情况在计算行时会计算一次，计算列时又计算了一次，因此要减去这些情况。
首先来计算某几行颜色相同的情况，由容斥原理可以知道，某几行颜色相同的情况等于至少一行颜色相同的情况，减去至少两行颜色相同的情况，加上至少三行颜色相同的情况……而至少 $t$ 行颜色相同的方案数为 $C_n^t\times3^t\times3^{n\times(n-t)}$，因此某几行颜色相同的方案数为：
$$\sum_{t=1}^n(-1)^{t+1}\times C_n^t\times3^t\times3^{n\times(n-t)}$$
某几列的计算方式与某几行的计算方式完全相同，所以直接将上式乘 $2$，即可得到某几行颜色相同与某几列颜色相同的方案数的和，而接下来要减去某几行与某几列颜色完全相同的情况。
同样地，这也是一个容斥，对于每一个 $i$ 行去枚举 $j$ 列，就是有 $i$ 行至少一列颜色相同的情况，减去有 $i$ 行至少两列颜色相同的情况，加上 $i$ 行至少 $3$ 列颜色相同的情况……在枚举 $i$ 行的时候也是同样的容斥。如果至少有 $i$ 行 $j$ 列的颜色完全相同，那么所有的方案数为 $3\times C_n^i\times C_n^j\times3^{(n-i)\times(n-j)}$，因此某几行某几列颜色完全相同的方案数为：
$$\sum_{i=1}^n\sum_{j=1}^n3\times C_n^i\times C_n^j\times(-1)^{i+j}\times3^{(n-i)\times(n-j)}$$
这个公式计算的复杂度为 $O(n^2)$，对题给数据范围 $1\leq n\leq10^6$ 显然是不满足在 $10^8$ 次计算内求得最终解的，因此需要化简，可以发现其中隐含了二项式 $(a+b)^n=\sum_{i=0}^nC_n^i\times a^i\times b^{n-i}$，对于每个固定的 $i$，将关于 $j$ 的项化简可以得到：
$$\sum_{i=1}^n3\times C_n^i\times(-1)^i\times\left[(3^{n-i}-1)^n-3^{(n-i)\times n}\right]$$
最终的结果就是：
$$2\times\sum_{t=1}^n(-1)^{t+1}\times C_n^t\times3^t\times3^{n\times(n-t)}-\sum_{i=1}^n3\times C_n^i\times(-1)^i\times\left[(3^{n-i}-1)^n-3^{(n-i)\times n}\right]$$
这个公式本身的计算次数是 $O(n)$ 的，但是由于存在幂运算，所以应该用快速幂将幂运算的时间复杂度降低到 $O(\log n)$，因此总的时间复杂度为 $O(n\log n)$。