@Dmaxiya 2020-12-12T07:26:27.000000Z 字数 6253 阅读 1250

Codeforces Round #439 (Div. 2)

Codeforces

Contests 链接：Codeforces Round #439 (Div. 2)
过题数：3
排名：623/10987

A. The Artful Expedient

题意

$Karen$ 和 $Koyomi$ 两个人分别列出 $n$ 个数字 $x_1,x_2,\cdots,x_n$ 和 $y_1,y_2,\cdots,y_n$ ，其中对于任意 $i,j(i\neq j)$ 有 $x_i\neq x_j,y_i\neq y_j$ ，问对于这个数组中有多少个 $(i,j)$ 对，使得 $x_i\bigoplus y_j$ 的值等于这两个序列当中的某一个数字，如果答案为偶数，则 $Karen$ 获胜，否则 $Koyomi$ 获胜。

输入

第一行为一个整数 $n~(1\leq n\leq2000)$ ，第二行为 $n$ 个互不相等的整数 $x_1,x_2,\cdots,x_n$ ，表示 $Karen$ 给出的 $n$ 个数字，第三行为 $n$ 个互不相等的整数 $y_1,y_2,\dots,y_n$ 表示 $Koyomi$ 给出的 $n$ 个数字，其中 $(1\leq x_i,y_i\leq2\times10^6)$

输出

输出获胜者的名字。

样例

输入	输出	提示
3 1 2 3 4 5 6	Karen	有 $6$ 对整数满足条件： $(1,1),(1,2),(2,1),(2,3),(3,2),(3,3)$ ，而 $6$ 是一个偶数，所以 $Karen$ 获胜。
5 2 4 6 8 10 9 7 5 3 1	Karen	总共有 $16$ 对整数满足条件，所以获胜者仍然是 $Karen$ 。

题解

把所有数字放到 $set$ 中，然后 $O(n^2)$ 枚举所有的数对 $(i,j)$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 2000 + 100;
int n;
int a[maxn], b[maxn];
set<int> st;
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        st.insert(a[i]);
    }
    for(int i = 1; i <= n; ++i) {
        scanf("%d", &b[i]);
        st.insert(b[i]);
    }
    int ans = 0;
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= n; ++j) {
            int Xor = a[i] ^ b[j];
            if(st.find(Xor) != st.end()) {
                ++ans;
            }
        }
    }
    if(ans % 2 == 0) {
        printf("Karen\n");
    } else {
        printf("Koyomi\n");
    }
    return 0;
}

B. The Eternal Immortality

题意

计算 $\frac{b!}{a!}$ 的个位数，其中 $x!=1\times2\times3\cdots\times x$ ，且 $0!=1$ 。

输入

输入只包含两个整数 $a$ 和 $b~(0\leq a\leq b\leq10^{18})$ 。

输出

输出 $\frac{b!}{a!}$ 的个位数。

样例

输入	输出	提示
2 4	2	$\frac{4!}{2!}=12$ ，个位数字是 $2$ 。
0 10	0	$\frac{10!}{0!}=3628800$ ，个位数是 $0$ 。
107 109	2	$\frac{109!}{107!}=11772$ ，个位数字是 $2$ 。

题解

阶乘的个位经常是 $0$ ，可以发现，只要 $a$ 和 $b$ 之间的距离超过 $5$ ， $\frac{b!}{a!}$ 的个位就是 $0$ （因为含有因子 $2$ 和 $5$ ）。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
LL a, b;
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    scanf("%I64d%I64d", &a, &b);
    if(b - a > 5) {
        printf("0\n");
    } else {
        LL ans = 1;
        for(LL i = a + 1; i <= b; ++i) {
            ans *= i;
            ans %= 10;
        }
        printf("%I64d\n", ans);
    }
    return 0;
}

C. The Intriguing Obsession

题意

有红、蓝、紫三种颜色的岛屿，岛屿数量分别为 $a,b,c$ ，要在岛屿之间建桥，每座桥的长度都为 $1$ ，问要使所有岛屿满足以下条件，总共有多少种桥的建法：

同一种颜色的任意两座岛屿之间的距离至少为 $3$ ；

每个岛屿的度最大为 $2$ 。

输入

输入包含三个整数 $a,b,c$ ，分别表示三种颜色的岛屿的数量。

输出

输出合法的建桥的方案数对 $998244353$ 取模后的结果。

样例

输入	输出	提示
1 1 1	8	能在三个岛屿之间建立的桥有三个，且即使三座桥同时建立也是合法的，所以总共的合法的方案数为 $2^3=8$ 。
1 2 2	63	对于 $a=1,b=c=2$ 的情况，下图中上面的两幅图是合法的建桥方案，下面的两幅图不是合法的建桥方案：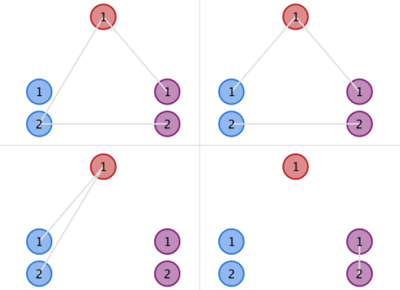
1 3 5	3264
6 2 9	813023575

题解

通过画样例可以发现，每座岛屿连出的两条边（桥）只能通向另外两种颜色的岛屿，对于任意两种颜色的岛屿 $a,b$ ，它们之间能连的边的数量为 $\min(a,b)$ ，可以从 $a$ 中选出 $\min(a,b)$ 个点与另一种颜色的 $b$ 个点中的 $\min(a,b)$ 连边，左右两边的点一一对应，总共有 $\min(a,b)!$ 种对应方式，所以方案数为 $C_a^{\min(a,b)}C_b^{\min(a,b)}\min(a,b)!$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 5000 + 100;
const LL MOD = 998244353LL;
int a, b, c;
LL ans;
LL C[maxn][maxn];
LL fac[maxn];
void Init() {
    C[0][0] = 1;
    for(int i = 1; i <= 5000; ++i) {
        for(int j = 0; j <= i; ++j) {
            if(j == 0 || j == i) {
                C[i][j] = 1;
            } else {
                C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
            }
        }
    }
    fac[0] = 1;
    for(int i = 1; i <= 5000; ++i) {
        fac[i] = (fac[i - 1] * i) % MOD;
    }
}
LL solve(int a, int b) {
    int Min = min(a, b);
    LL ret = 0;
    for(int i = 0; i <= Min; ++i) {
        ret = (ret + (((C[a][i] * C[b][i]) % MOD) * fac[i]) % MOD) % MOD;
    }
    return ret;
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    Init();
    scanf("%d%d%d", &a, &b, &c);
    ans = solve(a, b);
    ans = (ans * solve(b, c)) % MOD;
    ans = (ans * solve(a, c)) % MOD;
    printf("%I64d\n", ans);
    return 0;
}

E. The Untended Antiquity

题意

在一个 $n\times m$ 的网格上，进行 $q$ 次操作：

$1~r1~c1~r2~c2$ ：以在位置 $(r1,c1)$ 和 $(r2,c2)$ 上的两个方格为矩形的两个对角，画出矩形的边框，在矩形的边框上设置一圈障碍物；

$2~r1~c1~r2~c2$ ：以在位置 $(r1,c1)$ 和 $(r2,c2)$ 上的两个方格为矩形的两个对角，消去在这个矩形边框上的障碍物；

$3~r1~c1~r2~c2$ ：询问能否从位置 $(r1,c1)$ 不穿过障碍地到达位置 $(r2,c2)$ 。

输入

第一行为三个整数 $n,m,q~(1\leq n,m\leq2500,1\leq q\leq10^5)$ ，接下去 $q$ 行每行 $5$ 个整数 $t_i,r_{i1},c_{i1},r_{i2},c_{i2}$ ，表示每次操作的方式与对应的坐标，其中 $t_i\in[1,3],1\leq r_{i1},r_{i2}\leq n,1\leq c_{i1},c_{i2}\leq m$ ，且

当 $t_i=1$ 时， $2\leq r_{i1}\leq r_{i2}\leq n-1,2\leq c_{i1}\leq c_{i2}\leq m-1$ ，数据保证每个矩形的边框不会出现相交、重叠的情况；

当 $t_i=2$ 时， $2\leq r_{i1}\leq r_{i2}\leq n-1,2\leq c_{i1}\leq c_{i2}\leq m-1$ ，数据保证每一个 $t_i=2$ 中的坐标一定在之前的 $t_j=1$ 中出现过；

当 $t_i=3$ 时，没有额外的限制。

输出

对于每次 $t_i=3$ 的询问，如果可以不穿过障地从 $(r_{i1},c_{i1})$ 到达 $(r_{i1},c_{i2})$ ，就输出 $Yes$ ，否则输出 $No$ 。

样例

输入	输出	提示
5 6 5 1 2 2 4 5 1 3 3 3 3 3 4 4 1 1 2 2 2 4 5 3 1 1 4 4	No Yes	两次询问时的示意图如下：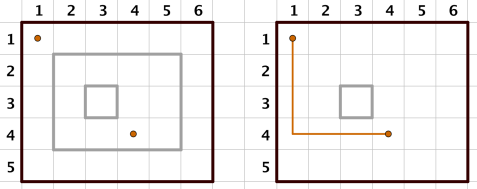
2500 2500 8 1 549 1279 1263 2189 1 303 795 1888 2432 1 2227 622 2418 1161 3 771 2492 1335 1433 1 2017 2100 2408 2160 3 48 60 798 729 1 347 708 1868 792 3 1940 2080 377 1546	No Yes No

题解

先考虑一个更简单些的问题，如果每次操作 $1$ 是将矩形区域上的所有数字都 $+1$ ，每次操作 $2$ 是 $-1$ ，而操作 $3$ 是询问两点上的值是否相等，就是一个二维树状数组的问题。现在再来思考这个问题，这两个问题其实是相似的，在题给问题中，对每个矩形编号，添加某个矩形的边框时将矩形区域内的数字都加上这个矩形的编号，删除某个矩形的边框时将矩形区域内的数字都减去这个矩形的编号。我们无法设计出一个编号方式使得对所有的矩形编号都不出现 $\sum_{i=1}^{k_1}ID_{x_i}=\sum_{i=1}^{k_2}ID_{y_i},x_i,y_i\in[1,rec\_cnt]$ ，只要出现这种情况，就会发生冲突，造成判断的结果出错，但是我们可以用随机编号的方式将这些编号求和出现冲突的概率降低，对每个新的矩形，将其编号为 $rand_1*rand_2$ ，就可以将冲突的概率降低到 $(rand_{max})^{-2}$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <sstream>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
#include <ctime>
using namespace std;
#define LL long long
const int maxn = 2500 + 100;
int n, m, q, t, r1, r2, c1, c2;
int sum[maxn][maxn], num[maxn][maxn];
int lowbit(int x) {
    return x & (-x);
}
void update(int i, int j, int x) {
    while(i <= n) {
        int jj = j;
        while(jj <= m) {
            sum[i][jj] += x;
            jj += lowbit(jj);
        }
        i += lowbit(i);
    }
}
int query(int i, int j) {
    int ret = 0;
    while(i > 0) {
        int jj = j;
        while(jj > 0) {
            ret += sum[i][jj];
            jj -= lowbit(jj);
        }
        i -= lowbit(i);
    }
    return ret;
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    srand((unsigned)time(NULL));
    while(scanf("%d%d%d", &n, &m, &q) != EOF) {
        memset(sum, 0, sizeof(sum));
        for(int i = 0; i < q; ++i) {
            scanf("%d%d%d%d%d", &t, &r1, &c1, &r2, &c2);
            int x;
            if(t == 1) {
                x = rand() * rand();
                num[r1][c1] = x;
            } else if(t == 2) {
                x = -num[r1][c1];
            }
            if(t != 3) {
                update(r1, c1, x);
                update(r1, c2 + 1, -x);
                update(r2 + 1, c1, -x);
                update(r2 + 1, c2 + 1, x);
            } else {
                int tmp1 = query(r1, c1);
                int tmp2 = query(r2, c2);
                if(tmp1 == tmp2) {
                    printf("Yes\n");
                } else {
                    printf("No\n");
                }
            }
        }
    }
    return 0;
}

Codeforces Round #439 (Div. 2)

A. The Artful Expedient

题意

输入

输出

样例

题解

过题代码

B. The Eternal Immortality

题意

输入

输出

样例

题解

过题代码

C. The Intriguing Obsession

题意

输入

输出

样例

题解

过题代码

E. The Untended Antiquity

题意

输入

输出

样例

题解

过题代码

内容目录