@Dmaxiya 2018-08-17T02:23:31.000000Z 字数 8014 阅读 1370

Codeforces Round #493 (Div. 2)

Codeforces

Contests 链接：Codeforces Round #493 (Div. 2)
过题数：4
排名：47/5210

A. Balloons

题意

总共有 $n$ 个袋子，第 $i$ 个袋子里放 $a_i$ 个气球，现在要把所有的袋子分成非空的两部分，要求第一部分的气球总数不等于第二部分的气球总数，输出合法的分配方案。

输入

第一行为一个整数 $n~(1\leq n\leq10)$ ，第二行为 $n$ 个整数 $a_1,a_2,\cdots,a_n~(1\leq a_i\leq1000)$ 。

输出

如果无法将所有袋子分成合法的两部分，输出 $-1$ ，否则在第一行输出一个整数 $k$ ，表示分给第一部分的袋子数，接下去一行为 $k$ 个整数，表示将编号为 $Index_i~(1\leq Index_i\leq n)$ 的袋子分到第一部分，如果有多解输出任意一组。

样例

输入	输出	提示
3 1 2 1	2 1 2	第一部分有 $3$ 个气球而第二部分有 $1$ 个气球。
2 5 5	-1	只有一种分法：第一个袋子分给第一部分，第二个袋子分给第二部分，而这种分法将使得第一部分的气球数量等于第二部分的气球。
1 10	-1	两部分中的任意一部分将会为空。

题解

如果 $n=1$ ，一定输出 $-1$ ，否则找出最小的数字 $a_j$ ，如果 $\sum_{i=1}^na_i-a_j\neq a_j$ ，则将这个数字分配到第一部分，否则输出 $-1$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100 + 100;
int n, sum, Min;
int num[maxn];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        sum = 0;
        Min = 1;
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
            if(num[i] < num[Min]) {
                Min = i;
            }
            sum += num[i];
        }
        if(n == 1) {
            printf("-1\n");
            continue;
        }
        if(sum - num[Min] == num[Min]) {
            printf("-1\n");
        } else {
            printf("1\n%d\n", Min);
        }
    }
    return 0;
}

B. Cutting

题意

给定一个长度为 $n$ 的数列，这个数列的奇数项的个数和偶数项的个数相等，将这个数列分割成多个数列，要让每个数列的奇数项个数都等于偶数项个数，如果在数列中的两个数字 $x$ 和 $y$ 之间分割，将花费 $|x-y|$ 个比特币，问在满足花费不超过 $B$ 个比特币的情况下，最多可以分割多少次。

输入

第一行包含两个整数 $n~(2\leq n\leq100)$ 和 $B~(1\leq B\leq100)$ ，第二行包含 $n$ 个整数 $a_1,a_2,\cdots,a_n~(1\leq a_i\leq100)$ ，其中奇数项的个数一定等于偶数项的个数。

输出

输出满足条件的最大分割次数。

样例

输入	输出	提示
6 4 1 2 5 10 15 20	1	最优的分割方式是在 $2$ 和 $5$ 之间，分割的花费为 $3\leq4$ 。
4 10 1 3 2 4	0	没有任何位置可以进行分割。
6 100 1 2 3 4 5 6	2	可以在 $2~3$ 和 $4~5$ 之间进行分割，花费为 $1+1=2\leq100$ 。

题解

首先预处理出每个可以分割的位置以及花费，将所有花费按从小到大排序，贪心地每次取花费最小的点进行分割，就能得到最多的分割次数。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100 + 100;
int n, B, tmp, cnt;
int num[maxn], sum[maxn];
int *it;
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &B) != EOF) {
        for(int i = 0; i < n; ++i) {
            scanf("%d", &num[i]);
        }
        tmp = 0;
        cnt = 0;
        for(int i = 0; i < n - 1; ++i) {
            if(num[i] % 2 == 0) {
                ++tmp;
            } else {
                --tmp;
            }
            if(tmp == 0) {
                sum[cnt++] = abs(num[i] - num[i + 1]);
            }
        }
        sort(sum, sum + cnt);
        for(int i = 1; i < cnt; ++i) {
            sum[i] += sum[i - 1];
        }
        it = upper_bound(sum, sum + cnt, B);
        printf("%d\n", it - sum);
    }
    return 0;
}

C. Convert to Ones

题意

对一个长度为 $n$ 的 $01$ 字符串，可以进行以下两种操作：

选择其中一个子串（也可以选择整个字符串），将这个子串翻转，这将花费 $x$ 元，例如： $01\underline{011}01\rightarrow01\underline{110}01$ ‘

选择其中一个子串，将这个子串中所有的 $0$ 变为 $1$ ，所有 $1$ 变为 $0$ ，这将花费 $y$ 元，例如： $01\underline{011}01\rightarrow01\underline{100}01$ 。

以上操作可以以任意顺序执行，问要将一个给定的 $01$ 字符串通过以上两种操作转化为全为 $1$ 的字符串，最小的花费是多少？

输入

第一行包含三个整数 $n,x,y~(1\leq n\leq3\times10^5,0\leq x,y\leq10^9)$ ，第二行为一个长度为 $n$ 的 $01$ 串。

输出

输出最少花费。

样例

输入	输出	提示
5 1 10 01000	11	首先你需要对子串 $[1,2]$ 进行操作 $1$ ，然后对子串 $[2,5]$ 进行操作 $2$ ，字符串变化过程为： $01000\rightarrow10000\rightarrow11111$ 总的花费为 $1+10=11$ 。
5 10 1 01000	2	首先你需要对子串 $[1,1]$ 进行操作 $2$ ，然后对子串 $[3,5]$ 进行操作 $2$ ，字符串的变化过程为： $01000\rightarrow11000\rightarrow11111$ 总的花费为 $1+1=2$
7 2 3 1111111	0	字符串本身就是一个全为 $1$ 的串，所以不需要进行任何操作。

题解

通过画样例可以发现，操作 $1$ 和操作 $2$ 的总操作次数等于字符串中 $0$ 的段数 $cnt$ ，且至少执行一次操作 $2$ ，所以可以从 $1$ 到 $cnt$ 枚举操作 $2$ 的次数，取花费的最小值就是答案。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 300000 + 100;
bool flag;
LL n, x, y, len, cnt, ans;
char str[maxn];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    while(scanf("%I64d%I64d%I64d", &n, &x, &y) != EOF) {
        ans = 1e18;
        cnt = 0;
        flag = false;
        scanf("%s", str);
        len = strlen(str);
        for(int i = 0; i <= len; ++i) {
            if(str[i] != '0') {
                if(flag) {
                    ++cnt;
                    flag = false;
                }
            } else {
                flag = true;
            }
        }
        if(cnt == 0) {
            printf("0\n");
            continue;
        }
        for(LL i = 1; i <= cnt; ++i) {
            ans = min(ans, i * y + (cnt - i) * x);
        }
        printf("%I64d\n", ans);
    }
    return 0;
}

D. Roman Digits

题意

在罗马数字和阿拉伯数字之间存在映射： $I\rightarrow1,V\rightarrow5,X\rightarrow10,L\rightarrow50$ ，对于任意一个由罗马数字组成的数字，它表示的数值等于每一位对应映射的和，如： $XXXV=35, IXI=12$ ，注意这里的表达方式和一般的罗马数字的表达方式不同， $IX$ 的值为 $11$ 而不是 $9$ ，如果现在有一个 $n$ 位的罗马数字，问这个罗马数字表示的值有几种可能的情况？

输入

输入只包含一个整数 $n~(1\leq n\leq10^9)$ 。

输出

输出为一个整数，表示用 $n$ 位罗马数字能够表示的不同的数字的个数。

样例

输入	输出	提示
1	4	可以表示的数字为： $I,V,X,L\rightarrow1,5,10,50$ 。
2	10	可以表示的数字为： $2(II),6(VI),10(VV),11(XI),15(XV),20(XX),51(IL),55(VL),60(XL),100(LL)$ 。
10	244

题解

通过暴力打表找规律到第 $100$ 项可以发现，除了前 $11$ 项是没有规律的，第 $12$ 项开始就是一个公差为 $49$ 的等差数列。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
LL n;
LL num[15] = {0, 4, 6, 10, 15, 21, 27, 33, 39, 43, 46, 48};
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    for(int i = 1; i <= 11; ++i) {
        num[i] += num[i - 1];
    }
    while(scanf("%I64d", &n) != EOF) {
        if(n <= 11) {
            printf("%I64d\n", num[n]);
            continue;
        }
        printf("%I64d\n", 292LL + 49LL * (n - 11));
    }
    return 0;
}

E. Sky Full of Stars

题意

在一个 $n\times n$ 的网格中，可以给每一格方格填充红、绿、蓝中的一种颜色，则总共有 $3^{n \times n}$ 种涂色方案，问在这些方案中，至少有一行或者一列颜色相同的涂色方案数。

输入

输入只包含一个整数 $n~(1\leq n\leq10^6)$ 。

输出

输出所有合法的涂色方案数对 $998244353$ 取模的结果。

样例

输入	输出	提示
1	3	由于只有一行一列，因此所有涂色方案都是合法的，总共有 $3^1=3$ 种涂色方案。
2	63	当 $n=2$ 时，以下两种涂色方案是合法的：而以下两种涂色方案是不合法的：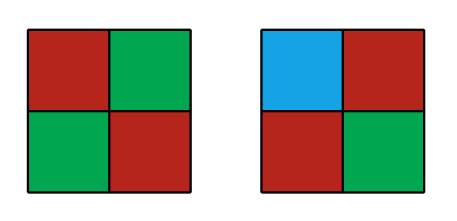
3	9933

题解

首先计算某几行以及某几列颜色相同的情况，如：

$\begin{matrix} BRG&GBB\\ GGG&GBB\\ GRB&RBB\\ \end{matrix}$
在这些情况中，颜色相同的所有行和列都为同一种颜色的情况会被重复计算如：

$\begin{matrix} GGG&RRR\\ RBG&RBG\\ RGG&RRR \end{matrix}$
这些情况在计算行时会计算一次，计算列时又计算了一次，因此要减去这些情况。
首先来计算某几行颜色相同的情况，由容斥原理可以知道，某几行颜色相同的情况等于至少一行颜色相同的情况，减去至少两行颜色相同的情况，加上至少三行颜色相同的情况……而至少 $t$ 行颜色相同的方案数为 $C_n^t\times3^t\times3^{n\times(n-t)}$ ，因此某几行颜色相同的方案数为：

$\sum_{t=1}^n(-1)^{t+1}\times C_n^t\times3^t\times3^{n\times(n-t)}$
某几列的计算方式与某几行的计算方式完全相同，所以直接将上式乘 $2$ ，即可得到某几行颜色相同与某几列颜色相同的方案数的和，而接下来要减去某几行与某几列颜色完全相同的情况。
同样地，这也是一个容斥，对于每一个 $i$ 行去枚举 $j$ 列，就是有 $i$ 行至少一列颜色相同的情况，减去有 $i$ 行至少两列颜色相同的情况，加上 $i$ 行至少 $3$ 列颜色相同的情况……在枚举 $i$ 行的时候也是同样的容斥。如果至少有 $i$ 行 $j$ 列的颜色完全相同，那么所有的方案数为 $3\times C_n^i\times C_n^j\times3^{(n-i)\times(n-j)}$ ，因此某几行某几列颜色完全相同的方案数为：

$\sum_{i=1}^n\sum_{j=1}^n3\times C_n^i\times C_n^j\times(-1)^{i+j}\times3^{(n-i)\times(n-j)}$
这个公式计算的复杂度为 $O(n^2)$ ，因此需要化简，可以发现其中隐含了二项式 $(a+b)^n=\sum_{i=0}^nC_n^i\times a^i\times b^{n-i}$ ，对于每个固定的 $i$ ，将关于 $j$ 的项化简可以得到：

$\sum_{i=1}^n3\times C_n^i\times(-1)^i\times\left[(3^{n-i}-1)^n-3^{(n-i)\times n}\right]$
最终的结果就是：

$2\times\sum_{t=1}^n(-1)^{t+1}\times C_n^t\times3^t\times3^{n\times(n-t)}-\sum_{i=1}^n3\times C_n^i\times(-1)^i\times\left[(3^{n-i}-1)^n-3^{(n-i)\times n}\right]$
这个公式本身的计算次数是 $O(n)$ 的，但是由于存在幂次，所以应该用快速幂将幂运算的时间复杂度降低到 $O(\log n)$ ，因此总的时间复杂度为 $O(n\log n)$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cfloat>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <ctime>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const LL MOD = 998244353;
const int maxn = 1000000 + 100;
LL n, ans;
LL inv[maxn], pro[maxn], invpro[maxn];
void Prepare_C() {
    inv[1] = 1;
    for(int i = 2; i < maxn; ++i) {
        inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
    }
    pro[0] = invpro[0] = 1;
    for(int i = 1; i < maxn; ++i) {
        pro[i] = pro[i - 1] * i % MOD;
        invpro[i] = invpro[i - 1] * inv[i] % MOD;
    }
}
LL get_C(LL n, LL m) {
    if(n < m) {
        return 0;
    }
    return pro[n] * invpro[m] % MOD * invpro[n - m] % MOD;
}
LL fast_pow(LL x, LL n) {
    LL ans;
    for(ans = 1; n != 0; n >>= 1) {
        if((n & 1) == 1) {
            ans = (ans * x) % MOD;
        }
        x = (x * x) % MOD;
    }
    return ans;
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif
    ios::sync_with_stdio(false);
    Prepare_C();
    while(scanf("%I64d", &n) != EOF) {
        ans = 0;
        for(LL i = 1; i <= n; ++i) {
            LL first = 1;
            LL second = 1;
            if(i % 2 == 0) {
                first = (-1 * first % MOD + MOD) % MOD;
                second = first;
            }
            first = 2 * first % MOD * get_C(n, i) % MOD * fast_pow(3, (n - i) * n + i) % MOD;
            LL tmp = ((fast_pow(3, n - i) - 1) % MOD + MOD) % MOD;
            tmp = ((fast_pow(tmp, n) - fast_pow(3, (n - i) * n)) % MOD + MOD) % MOD;
            second = 3 * second % MOD * get_C(n, i) % MOD * tmp % MOD;
            ans = (ans + first + second) % MOD;
        }
        printf("%I64d\n", ans);
    }
    return 0;
}

Codeforces Round #493 (Div. 2)

A. Balloons

题意

输入

输出

样例

题解

过题代码

B. Cutting

题意

输入

输出

样例

题解

过题代码

C. Convert to Ones

题意

输入

输出

样例

题解

过题代码

D. Roman Digits

题意

输入

输出

样例

题解

过题代码

E. Sky Full of Stars

题意

输入

输出

样例

题解

过题代码

内容目录