深度优先搜索

Hello_World

---

dfs

深度优先搜索 $(deep~first~search)$ 简称 $dfs$ /深搜，简单来说就是优先往“下一状态”进行搜索，在当前状态下，如果有下一步，就先搜索它的下一个状态，而不是并列状态，优先搜索并列状态的是 $bfs$（宽度优先搜索），这个后面再说。

1. 树上 dfs

先从最简单的树上 $dfs$ 开始，基本算法是从根节点出发，往第一个子节点$_1$搜索，如果子节点$_1$仍有子节点$_2$，则继续搜索子节点$_2$，直到叶子节点$_1$，再返回上一层$_1$，继续搜索上一层$_1$的第二个子节点$_3$，不断回溯直到搜索到最后一个叶子节点$_2$。
如下图，其 $dfs$ 顺序为

$$A\rightarrow B\rightarrow D\rightarrow(B)\rightarrow E\rightarrow(B)\rightarrow(A)\rightarrow C\rightarrow(A)$$

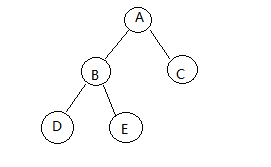
其中括号中的节点没有被重复搜索，只是深搜时回溯的顺序。将以上序列去掉括号中的节点，再按顺序将 $A~B~E~F~C~D$ 分别记为 $1~2~3~4~5~6$，就是这张图的 $dfs$ 序，$dfs$ 序可以通过一次深搜得到，由于 $dfs$ 序所具有的一些性质，其在 $LCA$、线段树构图等算法中有重要作用，这还需在学习 $ST$ 表、线段树等知识后再讲解，这里不进行展开。
有向树（只存在从父节点指向子节点的边）上搜索代码如下：

void dfs(int x) {
    /*当前节点 x 初始化操作*/
    int len = G[x].size();
    for(int i = 0; i < len; ++i) {
        int pos = G[x][i];
        /*更新 pos 节点前的操作*/
        dfs(pos);
        /*更新 pos 节点后的操作*/
    }
    /*遍历所有子节点后对 x 节点有关的操作*/
}

无向树（每条边都有两个方向）上搜索代码如下：

void dfs(int f, int x) {
    // f 为当前节点 x 的父节点
    /*对 x 节点初始化操作*/
    int len = G[x].size();
    for(int i = 0; i < len; ++i) {
        int pos = G[x][i];
        if(pos != f) {
            /*更新 pos 节点前的操作*/
            dfs(x, pos);
            /*更新 pos 节点后的操作*/
        }
    }
    /*遍历所有子节点后对 x 节点有关的操作*/
}

现在看起来文字描述比较多，只是因为还没有讲到图在计算机上的储存方式，做到有关图上算法的练习后，会更新上面的代码。
其实对于有向树上的 $dfs$ 操作也可以用无向树上 $dfs$ 操作的代码，两种写法区别不大，理解一种自然理解了另一种。

2. 图上 dfs

树有一个很重要的性质是没有环，没有环的图就是一棵树。
图上的 $dfs$ 算法步骤和树上 $dfs$ 一模一样，只是由于图上存在环，所以需要加一个 $vis$ 数组，表示当前节点已经被搜索过，不再进行搜索，如果不用 $vis$ 数组进行标记，深搜算法将一直在环上搜索。
下面这张图从 $F$ 节点开始 $dfs$ 的顺序（为体现 $vis$ 数组的作用，下面的序列采用了一种比较奇怪的顺序进行深搜）如下（括号中的节点为已经 $vis$ 过，不再进行搜索的节点，序列不包含回溯节点）：

$$F\rightarrow H\rightarrow I\rightarrow C\rightarrow A\rightarrow D\rightarrow(F)\rightarrow B\rightarrow (C)\rightarrow E\rightarrow G$$

void dfs(int x) {
    /*当前节点 x 初始化操作*/
    vis[x] = true;
    int len = G[x].size();
    for(int i = 0; i < len; ++i) {
        int pos = G[x][i];
        if(!vis[pos]) {
            /*更新 pos 节点前的操作*/
            dfs(pos);
            /*更新 pos 节点后的操作*/
        }
    }
    /*遍历所有子节点后对 x 节点有关的操作*/
}

无论是有向图还是无向图，深搜代码都相同，因为有向图上仍然存在类似 $A\rightarrow B\rightarrow C\rightarrow A$ 的环，树是一种特殊的图，所以树上搜索也可以用这一段代码，但是建议图上 $dfs$ 与树上 $dfs$ 代码分开理解，因为树上有许多性质是图上所没有的。

4. 解空间的 dfs

深度优先搜索不但可以应用在图上，也可以在解空间上进行搜索，可以将每一个状态看成一个节点，一般解空间的搜索是在一棵树上进行的，每一个解的状态可以衍生出后继的几个状态，但通常不会搜索到之前的状态。
解空间的深搜代码如下：

void dfs(/*当前状态*/) {
    if(/*搜索到最终状态*/) {
        /*判断解是否合法，并做相应操作*/
        return ;
    }
    for(/*搜索所有后继状态*/) {
        if(/*该后继状态合法*/) {
            /*改变为后继状态*/
            dfs(/*该后继状态*/)
            /*修改为当前状态*/
        }
    }
}

这是解空间 $dfs$ 的基本模板，一般题目的深搜直接套用就行，但是在写的时候一定要注意每一步是否考虑到了，即使上面的某一步在代码中不必写到，但是写的时候一定要思考是否可以省略这一步，不能去想是否要加上这一步，从第二个方向考虑，容易因为漏考虑某些情况而省略代码。

2 月 8 日 dfs 练习题解

A. N皇后问题

题解

$n$ 皇后问题，只要用一个大小为 $n$ 的一维数组，$num_i$ 表示第 $i$ 行的皇后放在第 $num_i$ 列的位置就可以表示所有的状态，而且判断皇后位置是否合法也比二维数组更加容易。
深搜思路为：从第 $0$ 行开始搜索，对于第 $i$ 行的第 $num_i$ 列，判断是否存在 $j<i$ 且 $num_j\neq num_i~\&\&~abs(i-j)\neq abs(num_i-num_j)$，第一个不等号是用来判断前面几行中是否存在放置在 $num_i$ 列的皇后，第二个不等号是用来判断是否存在与第 $i$ 个皇后互为对角线的皇后，知道搜索到第 $n$ 行，说明这种情况是合法的，答案$++$。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100;
int n;
int num[maxn];
int put[maxn];
bool judge(int x, int y) {
    for(int i = 0; i < x; ++i) {
        if(put[i] == y || abs(x - i) == abs(y - put[i])) {
            return false;
        }
    }
    return true;
}
void dfs(int depth, int n) {
    if(depth == n) {
        ++num[n];
        return ;
    }
    for(int i = 0; i < n; ++i) {
        if(judge(depth, i)) {
            put[depth] = i;
            dfs(depth + 1, n);
        }
    }
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    for(int i = 1; i <= 10; ++i) {
        dfs(0, i);
    }
    while(scanf("%d", &n), n != 0) {
        printf("%d\n", num[n]);
    }
    return 0;
}

B. Sudoku Killer

题解

从第一个数字开始搜索，对于每一个问号，对其尝试填入 $1$ 到 $9$，如果存在一个合法的可以填入的数字（当前行、列、九宫格不存在与其相等的数字），就将该数字填入，并继续往下一格搜索。直到搜索到最后一格。
程序中运用了一些行列下标运算的技巧，将二维 $(x,y)$ 与一个数字 $depth$ 进行一一映射，这样就可以直接从 $depth=0$ 到 $depth=80$ 进行搜索，而不需要每行末尾的判断。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 20;
char str[maxn][maxn];
int num[maxn][maxn];
int cas = 0;
bool flag;
bool judge(int x, int y, int n) {
    for(int i = 0; i < 9; ++i) {
        if(num[i][y] == n || num[x][i] == n) {
            return false;
        }
    }
    int xx = x / 3 * 3;
    int yy = y / 3 * 3;
    for(int i = 0; i < 3; ++i) {
        for(int j = 0; j < 3; ++j) {
            if(num[xx + i][yy + j] == n) {
                return false;
            }
        }
    }
    return true;
}
void dfs(int depth) {
    if(depth == 81) {
        flag = true;
        return ;
    }
    int x = depth / 9;
    int y = depth % 9;
    if(num[x][y] == 0) {
        for(int i = 1; i <= 9; ++i) {
            if(judge(x, y, i)) {
                num[x][y] = i;
                dfs(depth + 1);
                if(flag) {
                    return ;
                }
                num[x][y] = 0;
            }
        }
    } else {
        dfs(depth + 1);
    }
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%s", str[0]) != EOF) {
        if(cas != 0) {
            printf("\n");
        }
        ++cas;
        flag = false;
        for(int i = 1; i < 9; ++i) {
            scanf("%s", str[0] + i);
        }
        for(int i = 1; i < 9; ++i) {
            for(int j = 0; j < 9; ++j) {
                scanf("%s", str[i] + j);
            }
        }
        for(int i = 0; i < 9; ++i) {
            for(int j = 0; j < 9; ++j) {
                if(str[i][j] == '?') {
                    num[i][j] = 0;
                } else {
                    num[i][j] = str[i][j] - '0';
                }
            }
        }
        dfs(0);
        for(int i = 0; i < 9; ++i) {
            for(int j = 0; j < 9; ++j) {
                if(j != 0) {
                    printf(" ");
                }
                printf("%d", num[i][j]);
            }
            printf("\n");
        }
    }
    return 0;
}

C. 连连看

题解

这题相对于一般的路径搜索多了一个：最多转弯两次的限制，实际上这题和一般搜索的代码完全相同，只是在判断时多加一个转弯次数的判断罢了，如果转弯次数超过两次，直接返回“不可行”，否则继续搜索下一层，对于每一个“下一层”的搜索，只要存在一个“可行”的路径，当前状态就是可行的，只有所有后继状态都不可行时，当前状态才是不可行的。
对于初始位置，应将方向初始化为与四个方向都不相同的方向，并将方向改变的次数初始化为 $-1$。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 1000 + 100;
int n, m, q;
int xx1, yy1, xx2, yy2;
int num[maxn][maxn];
const int dir[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int judge(int x, int y) {
    if(x < 1 || x > n || y < 1 || y > m) {
        return 0;
    }
    if(x == xx2 && y == yy2) {
        return 1;
    }
    if(num[x][y] != 0) {
        return 0;
    } else {
        return -1;
    }
}
bool dfs(int x, int y, int d, int cnt) {
    if(cnt == 3) {
        return false;
    }
    if(x == xx2 && y == yy2) {
        return true;
    }
    bool flag = false;
    for(int i = 0; i < 4; ++i) {
        int xx = x + dir[i][0];
        int yy = y + dir[i][1];
        int tmp = judge(xx, yy);
        if(tmp != 0) {
            if(tmp == -1) {
                num[xx][yy] = -1;
            }
            if(i != d) {
                if(dfs(xx, yy, i, cnt + 1)) {
                    flag = true;
                }
            } else {
                if(dfs(xx, yy, i, cnt)) {
                    flag = true;
                }
            }
            if(tmp == -1) {
                num[xx][yy] = 0;
            }
            if(flag) {
                break;
            }
        }
    }
    return flag;
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &m), n != 0 || m != 0) {
        for(int i = 1; i <= n; ++i) {
            for(int j = 1; j <= m; ++j) {
                scanf("%d", &num[i][j]);
            }
        }
        scanf("%d", &q);
        for(int i = 0; i < q; ++i) {
            scanf("%d%d%d%d", &xx1, &yy1, &xx2, &yy2);
            if(num[xx1][yy1] != num[xx2][yy2] || num[xx1][yy1] == 0 || num[xx2][yy2] == 0) {
                printf("NO\n");
                continue;
            }
            if(dfs(xx1, yy1, -1, -1)) {
                printf("YES\n");
            } else {
                printf("NO\n");
            }
        }
    }
    return 0;
}

2 月 9 - 10 日 dfs 练习

A. Red and Black

题意

一个 $n\times m$ 的网格中，一个人在 $'@'$ 字符所在的位置，他可以向上下左右四个方向走动，且他只能走在 $.$ 的格子上，不能穿过 $'\#'$ 的格子，问他可以到达的方格数量，输入到 $0~0$ 结束。

数据范围

$0\leq n,m\leq20$

题解

从 $'@'$ 点所在位置开始 $dfs$，将经过的点标记,对于每个位置搜索上下左右四个方向能够到达且没有呗标记的点，最后输出标记的点数。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 50;
int n, m, x, y, ans;
char str[maxn][maxn];
const int dir[4][2] =  {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
bool in(int x, int y) {
    return (x >= 0 && x < n && y >= 0 && y < m);
}
void dfs(int x, int y) {
    for(int i = 0; i < 4; ++i) {
        int xx = x + dir[i][0];
        int yy = y + dir[i][1];
        if(in(xx, yy) && str[xx][yy] == '.') {
            ++ans;
            str[xx][yy] = '#';
            dfs(xx, yy);
        }
    }
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &m, &n), n != 0 || m != 0) {
        ans = 1;
        for(int i = 0; i < n; ++i) {
            scanf("%s", str[i]);
            for(int j = 0 ; j < m; ++j) {
                if(str[i][j] == '@') {
                    x = i;
                    y = j;
                }
            }
        }
        dfs(x, y);
        printf("%d\n", ans);
    }
    return 0;
}

B. A 计划

题解

$dfs$ 思路和上一题相同，只是多了一个时间 $t$ 的限制（要在 $t$ 时刻内解救公主），超过 $t$ 步还没有拯救到公主，则不能沿这条路径拯救公主，以及到达 $'\#'$ 字格时，需要立即到另一层。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100;
int T, n, m, t;
bool flag;
char str[2][maxn][maxn];
bool vis[2][maxn][maxn];
const int dir[4][2] =  {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
bool in(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < m;
}
void dfs(int f, int x, int y, int t) {
    if(t == -1) {
        return ;
    }
    if(str[f][x][y] == 'P') {
        flag = true;
        return ;
    }
    int ff;
    for(int i = 0; i < 4; ++i) {
        int xx = x + dir[i][0];
        int yy = y + dir[i][1];
        if(in(xx, yy)) {
            if(str[f][xx][yy] == '#') {
                ff = 1 - f;
            } else {
                ff = f;
            }
            if(!vis[ff][xx][yy]) {
                vis[ff][xx][yy] = true;
                if(str[ff][xx][yy] == '.' || str[ff][xx][yy] == 'P') {
                    dfs(ff, xx, yy, t - 1);
                    if(flag) {
                        return ;
                    }
                }
                vis[ff][xx][yy] = false;
            }
        }
    }
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    scanf("%d", &T);
    while(T--) {
        flag = false;
        memset(vis, 0, sizeof(vis));
        scanf("%d%d%d", &n, &m, &t);
        for(int i = 0; i < 2; ++i) {
            for(int j = 0; j < n; ++j) {
                scanf("%s", str[i][j]);
            }
        }
        vis[0][0][0] = true;
        dfs(0, 0, 0, t);
        if(flag) {
            printf("YES\n");
        } else {
            printf("NO\n");
        }
    }
    return 0;
}

C. 逃离迷宫

题解

$dfs$ 过程中存一个转弯次数，搜索的时候，如果方向和原来的方向不一致，则转弯次数 $+1$，如果转弯次数大于 $k$，则不能从这条路径到达目标。注意这题需要剪枝，一个是一次 $dfs$ 过程中走过的路不能再走，一个是如果到达某个点时的转弯次数超过之前搜索到达这个点时的转弯次数，则不再进行搜索。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 200;
int T, n, m;
int xx1, yy1, xx2, yy2;
int cnt, k;
bool flag;
char str[maxn][maxn];
bool vis[maxn][maxn];
int ccnt[maxn][maxn];
const int dir[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
bool in(int x, int y) {
    return x > 0 && x <= n && y > 0 && y <= m;
}
void dfs(int x, int y, int d, int cnt) {
    if(cnt > ccnt[x][y]) {
        return ;
    } else {
        ccnt[x][y] = cnt;
    }
    if(cnt == k + 1) {
        return ;
    }
    if(x == xx2 && y == yy2) {
        flag = true;
        return ;
    }
    for(int i = 0; i < 4; ++i) {
        int xx = x + dir[i][0];
        int yy = y + dir[i][1];
        if(in(xx, yy) && str[xx][yy] == '.' && !vis[xx][yy]) {
            vis[xx][yy] = true;
            if(i == d) {
                dfs(xx, yy, i, cnt);
            } else {
                dfs(xx, yy, i, cnt + 1);
            }
            vis[xx][yy] = false;
            if(flag) {
                return ;
            }
        }
    }
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    scanf("%d", &T);
    while(T--) {
        flag = false;
        memset(vis, 0, sizeof(vis));
        memset(ccnt, 0x3f, sizeof(ccnt));
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; ++i) {
            scanf("%s", str[i] + 1);
        }
        scanf("%d%d%d%d%d", &k, &yy1, &xx1, &yy2, &xx2);
        dfs(xx1, yy1, -1, -1);
        if(flag) {
            printf("yes\n");
        } else {
            printf("no\n");
        }
    }
    return 0;
}