三种常用构图方式

博文

这篇博客讲的不是按像素计算的图片或者摄影摄像的构图，而是节点与节点之间有边、边上有权值的图，如何把这样的一张图存入计算机中。这里将介绍三种较为常用的构图方式：邻接矩阵、vector 数组和链式前向星构图。
首先要弄清楚的一点是，计算机存图，存的是什么？包含两部分：节点和边，每个节点都有自己相应的信息，例如在一个战争时期军人的调度问题，每个城池拥有的军人数量，或者染色问题上节点的颜色等等，这些就是节点上的信息。每条边上的信息就比如说是路程、路费，从这个节点出发的目标节点等等。一般来说节点和边是要分两个结构体 Node 和 Edge 来存的，但是很多题目基本上只有边的信息，节点基本没有信息，所以有时候可以不用写节点的结构体，如果边没有权值等其他信息，只需要知道一条边连接的是哪两个节点，连边的结构体也不用写了。这里只讨论有向图的一般情况。

邻接矩阵构图

无权图

邻接矩阵用第 $u$ 行第 $v$ 列为 $1$ 表示从 $u$ 到 $v$ 有一条边，用 $0$ 表示从 $u$ 到 $v$ 没有直接相连的边。

有权图

先设定一个无穷大数 $\infty$，则用第 $u$ 行第 $v$ 列为一非无穷大数值 $weight$ 表示从 $u$ 到 $v$ 之间，边的权值为 $weight$，为一无穷大数 $\infty$ 则表示从 $u$ 到 $v$ 没有直接相连的边或者不可达。
在图没有经过任何处理的情况下，$\infty$ 表示“无直接相连的边”，如果已经处理出全图的最短路径，则 $\infty$ 表示“不可达”，故可以根据处理出全图最短路径后的图是否存在 $\infty$ 的边来判断全图是否连通，当然判断连通图有更快的并查集的做法，不推荐上面这种方法来判断图的连通性。

图上加边代码

struct Edge {
    int weight;     // 权值
};
Edge G[maxn][maxn];
void add(int u, int v, int w) {
    G[u][v].weight = w;
}

遍历 $u$ 点的目标节点代码

void traversal(int u) {
    for(int i = 0; i < n; ++i) {    // n 为图上实际节点数
        visit(G[u][i]);
    }
}

邻接矩阵性质

• 初始状态下，第 $u$ 行所有非 $0/\infty$ 的列所对应的节点，即从 $u$ 出发能够到达的所有节点，其数量即 $u$ 的出度，第 $v$ 列所有非 $0/\infty$ 的行对应的节点，即能够到达 $v$ 的所有节点，其数量即 $v$ 的入度。
• 如果整张图有 $n$ 个节点，则邻接矩阵构图的空间复杂度为 $O(n^2)$，在图上宽搜和深搜的时间复杂度都为 $O(n^2)$。这种构图方式适用的算法：floyd 多源最短路径算法，该算法的时间复杂度为 $O(n^3)$，编程难度较低，适用于图上节点数 200 以下的图。
• 除了需要用 floyd 查找多源最短路径，其他情况均不推荐这种构图方式。

vector 数组构图

数据结构课本上提到过邻接链表构图，大意如下：
先定义一个链表数组，该数组下标对应图上所有节点，如果节点 $u$ 添加一条到 $v$ 的边，则在数组第 $u$ 个链表后面添加一条指向 $v$ 节点的边。
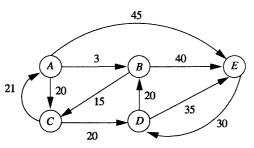
对于图

如果加边顺序如下 [u v w]：
[A E 45] [A B 3] [B E 40] [C A 21] [A C 20] [B C 15] [D B 20] [D E 35] [E D 30] [C D 20]
其邻接矩阵表示为：
G[A] → [E 45] → [B 3] → [C 20] → NULL
G[B] → [E 40] → [C 15] → NULL
G[C] → [A 21] → [D 20] → NULL
G[D] → [B 20] → [E 35] → NULL
G[E] → [D 30] → NULL
可以看到，图上有多少条边，就只需要多少内存，不会像邻接矩阵那样有大量的空间浪费。
C++ 的 STL 为我们提供了强大的容器类，使得我们不必手打链表、可变长数组等，所以我们可以直接用已经写好的类。但是为什么用 vector 而不用 list 呢？因为在算法题中时间是很重要的，动态开辟内存会带来很大的时间开销，因此我们更经常用 vector 数组来代替链表数组，以节约时间上的开销。

图上加边代码

struct Edge {
    int weight;         // 权值
    int to;             // 终点节点下标
    Edge(int w, int t) {
        weight = w;
        to = t;
    }
    Edge() {}
};
vector<Edge> G[maxn];
void add(int u, int v, int w) {
    G[u].push_back(Edge(w, v));
}

遍历 $u$ 点的目标节点代码

void traversal(int u) {
    int len = G[u].size();
    for(int i = 0; i < len; ++i) {
        visit(G[u][i]);
    }
}

vector 数组性质

• G[u].size() 即节点 $u$ 的出度，想要求节点 $v$ 的入度时间复杂度为 $O(e)$，$e$ 为图上所有边的数量，如果需要建议在建图的时候就用一个 degin 辅助数组来存放所有节点的入度。
• 边的存储顺序与加边顺序有关。
• 如果图上有 $e$ 条边，vector 数组的空间复杂度为 $O(e)$，宽搜和深搜的时间复杂度都为 $O(e)$，其他算法的时间复杂度由算法的优化程度决定，vector 数组构图不会增加算法的时间复杂度。
• vector 数组构图代码较短效率较高，推荐使用该方式。

链式前向星构图

在链式前向星之前还有一种叫前向星的构图方式，该方法在加完所有边后还需要进行一次排序，时间复杂度为 $O(e\log e)$，其中 $e$ 为图上所有边的数量，链式前向星是该方式的改进，这里不对前向星展开讨论。
链式前向星将所有边存在一个 Edge 数组中，并在边上加了一个 next 数据成员，表示与该边同起点的下一条边、在该数组中的下标。是的，链式前向星存的边并不是连续的，并不是将同起点的所有边存在一起，而是像链表一样，在一条边中存着下一条边的地址（数组下标）。
那么在所有的边中，怎么找到最开始的那条边呢？这里需要一个 head 数组，来存放所有相同起点的第一条边所在下标，实际上 head 数组存放的是：当前起点最后添加进去的边的下标，而边的 next 数据成员，指向的是：在加这条边之前，最后加进去的一条边的下标（也就是 head 数组对应的值），而这个下标必然是小于当前边的下标的，所以 next 数据成员实际上存放的是比当前边的下标更小的值。
而最先加入的那一条边指向的下标是 -1（或 0），所以 head 数组应初始化为 -1（或 0）。

图上加边代码

memset(head, -1, sizeof(head));    // main 函数中的预处理
struct Edge {
    int weight;         // 权值
    int to;             // 终点节点下标
    int Next;           // 下一条边的下标
    Edge(int w, int t, int n) {
        weight = w;
        to = t;
        Next = n;
    }
    Edge() {}
};
// vector 写法
vector<Edge> E;
int head[maxn];
void add(int u, int v, int w) {
    E.push_back(Edge(w, v, head[u]));
    head[u] = E.size() - 1;
}
// 定长数组写法
Edge E[maxm];           // maxm 为题目给定的最多的边数
int head[maxn];
int cnt;
void add(int u, int v, int w) {
    E[cnt].weight = w;
    E[cnt].to = v;
    E[cnt].Next = head[u];
    head[u] = cnt++;
}

遍历$u$ 点的目标节点代码

void traversal(int u) {
    for(int i = head[u]; i != -1; i = E[i].Next) {
        visit(E[i]);
    }
}

链式前向星性质

• 图上所有点的入度与出度需要用另外的数组来维护，如果在解题过程中需要对节点进行排序，请将 head、deg 数组作为 Node 结构体的数据成员。
• 其他性质与 vector 数组第 2、3 点相同。