@Dmaxiya 2018-08-17T02:25:38.000000Z 字数 7661 阅读 1226

Codeforces Round #490 (Div. 3)

Codeforces

Contests 链接：Codeforces Round #490 (Div. 3)
过题数：5
排名：125/7615

A. Mishka and Contest

题意

给出 $n$ 个问题的难度等级序列， $Mishka$ 只能解决难度等级不大于 $k$ 的问题，她每次解决问题都是从序列的前面或者后面选一个问题，如果她可以解决这个问题，那么这个问题就会从序列中删掉，她将会重复这个操作，直到她无法解决任何问题为止，问题她最多能解决多少问题。

输入

第一行为两个整数 $n$ 和 $k~(1\leq n,k\leq 100)$ ，第二行有 $n$ 个整数 $a_1,a_2,\cdots,a_n~(1\leq a_i\leq100)$ ，表示问题的难度。

输出

输出 $Mishka$ 能解决的最多的问题数。

样例

输入	输出	提示
8 4 4 2 3 1 5 1 6 4	5	$Mishka$ 可以按照 [4,2,3,1,5,1,6,4] $\rightarrow$ [2,3,1,5,1,6,4] $\rightarrow$ [2,3,1,5,1,6] $\rightarrow$ [3,1,5,1,6] $\rightarrow$ [1,5,1,6] $\rightarrow$ [5,1,6] 的顺序最多解决 $5$ 个问题。
5 2 3 1 2 1 3	0	由于序列两端的问题难度都大于 $2$ ，所以 $Mishka$ 无法解决任何问题。
5 100 12 34 55 43 21	5	$Mishka$ 可以解决所有问题。

题解

先判断序列中是否有大于 $k$ 的项，如果没有则直接输出 $n$ ，否则从两端找到最多的不大于 $k$ 的数字个数相加。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
typedef long long LL;
const int maxn = 200;
int n, k;
int num[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &k) != EOF) {
        bool flag = true;
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
            if(num[i] > k) {
                flag = false;
            }
        }
        if(flag) {
            printf("%d\n", n);
            continue;
        }
        int cnt = 0;
        for(int i = 1; i <= n; ++i) {
            if(num[i] > k) {
                break;
            }
            ++cnt;
        }
        for(int i = n; i >= 1; --i) {
            if(num[i] > k) {
                break;
            }
            ++cnt;
        }
        printf("%d\n", cnt);
    }
    return 0;
}

B. Reversing Encryption

题意

对一个长度为 $n$ 的字符串，从 $n$ 到 $1$ 枚举 $n$ 的所有因数 $d$ ，将字符串在区间 $[1,d]$ 上的所有字符反转，将得到一个新的字符串，如："codeforces" $\frac{d=10}{}$ "secrofedoc" $\frac{d=5}{}$ "orcesfedoc" $\frac{d=2}{}$ "rocesfedoc" $\frac{d=1}{}$ "rocesfedoc"。
现在给出进行以上操作之后的字符串，输出原字符串。

输入

第一行为一个整数 $n~(1\leq n\leq100)$ ，第二行为一个长度为 $n$ 的字符串 $t$ ， $t$ 仅包含小写字符。

输出

输出原字符串。

样例

输入	输出
10 rocesfedoc	codeforces
16 plmaetwoxesisiht	thisisexampletwo
1 z	z

题解

从 $1$ 到 $n$ 枚举所有 $n$ 的因数 $d$ ，将区间 $[1,d]$ 内的所有字符反转，就能得到原字符串。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
typedef long long LL;
const int maxn = 100 + 100;
int n;
char str[maxn];
void Reverse(int Index) {
    for(int i = 1; i <= Index / 2; ++i) {
        swap(str[i], str[Index - i + 1]);
    }
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        scanf("%s", str + 1);
        for(int i = 1; i <= n; ++i) {
            if(n % i == 0) {
                Reverse(i);
            }
        }
        printf("%s\n", str + 1);
    }
    return 0;
}

C. Alphabetic Removals

题意

给出一个长度为 $n$ 的只包含小写字符的字符串 $s$ ，输出对 $s$ 进行 $k$ 次以下操作后的字符串：

如果字符串内含有字符 'a'，则删掉最左边的那个 'a'，否则进入下一步；

如果字符串内含有字符 'b'，则删掉最左边的那个 'b'，否则进入下一步；
$\cdots\cdots$

如果字符串内有 'z'，则删掉最左边的 'z'。

输入

第一行为两个整数 $n$ 和 $k~(1\leq k\leq n\leq4\times10^5)$ ，第二行为一个字符串 $s$ 。

输出

输出经过 $k$ 次删除字符的操作的字符串。

样例

输入	输出
15 3 cccaabababaccbc	cccbbabaccbc
15 9 cccaabababaccbc	cccccc
1 1 u

题解

先统计每个字符出现的次数，然后根据 $k$ 计算出每个字符要删除多少次，然后 $O(n)$ 跑一遍整个字符串，每跑到一个字符就判断这个字符是否需要删除，如果需要删除就将该字符需要删除的次数减一，否则输出这个字符。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
typedef long long LL;
const int maxn = 400000 + 100;
int n, k;
char str[maxn];
int cnt[30], Del[30];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &k) != EOF) {
        memset(cnt, 0, sizeof(cnt));
        memset(Del, 0, sizeof(Del));
        scanf("%s", str);
        for(int i = 0; i < n; ++i) {
            ++cnt[str[i] - 'a'];
        }
        int Index = 0;
        while(k > 0) {
            if(k > cnt[Index]) {
                Del[Index] = cnt[Index];
                k -= cnt[Index];
                ++Index;
            } else {
                Del[Index] = k;
                break;
            }
        }
        for(int i = 0; i < n; ++i) {
            if(Del[str[i] - 'a'] <= 0) {
                putchar(str[i]);
            }
            --Del[str[i] - 'a'];
        }
        printf("\n");
    }
    return 0;
}

D. Equalize the Remainders

题意

给定两个整数 $n$ 和 $m$ ，保证 $\frac{n}{m}$ 为整数，以及 $n$ 个整数的序列 $a_i$ ， $c_i$ 表示序列中对 $m$ 取模等于 $i$ 的数字个数。
现在你可以对这个序列进行修改，每次修改可以将序列中的某个数字 $+1$ ，问最少需要多少次修改，能够使得 $c_0=c_1=c_2=\dots=c_{m-1}=\frac{n}{m}$ ，并输出修改后的序列。

输入

第一行为两个整数 $n$ 和 $m~(1\leq m\leq n\leq 2\times10^5)$ ，数据保证 $n\%m=0$ ，第二行为 $n$ 个整数 $a_1,a_2,\cdots,a_n~(0\leq a_i\leq10^9)$ 。

输出

第一行输出要使 $c_0=c_1=c_2\cdots=c_{m-1}=\frac{n}{m}$ 的最少修改次数，第二行为 $n$ 个整数，表示修改后的序列，如果有多解，输出任意一组，输出要保证每个数字都不应超过 $10^{18}$ 。

样例

输入	输出
6 3 3 2 0 6 10 12	3 3 2 0 7 10 14
4 2 0 1 2 3	0 0 1 2 3

题解

这题整体的思路就是贪心，如果 $c_i$ 大于 $\frac{n}{m}$ 个，将其中多出来的数字转化成离他“最近”的 $c_j$ 小于 $\frac{n}{m}$ 的数字。
思路很好想，就是代码的实现上如果没想清楚的话可能会写得很复杂，我的写法是这样的：用一个 $vector$ 数组来存，第 $i$ 个 $vector$ 存的是所有的对 $m$ 取模等于 $i$ 的数字的下标，然后一直调整 $vector$ 中的数字个数，直到所有 $vector$ 的大小都等于 $\frac{n}{m}$ 为止，调整的方法是：用一个 $Index$ 来跑 $vector$ 数组的那个 $i$ ，同时用一个队列，如果第 $Index$ 个 $vector$ 的 $size$ 大于 $\frac{n}{m}$ ，就把第 $Index$ 个 $vector$ 后面的元素放入队列，如果第 $Index$ 个 $vector$ 的 $size$ 小于 $\frac{n}{m}$ ，就把队首元素弹出，放到这个 $vector$ 后面，并将这个元素弹出队列， $Index$ 的跑法是 $Index=(Index+1)\% m$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
typedef long long LL;
const int maxn = 200000 + 100;
int n, m;
int num[maxn];
vector<int> G[maxn];
queue<int> que;
bool vis[maxn];
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n, &m) != EOF) {
        for(int i = 0; i < m; ++i) {
            G[i].clear();
            vis[i] = false;
        }
        int k = n / m;
        for(int i = 1; i <= n; ++i) {
            scanf("%d", &num[i]);
            G[num[i] % m].push_back(i);
        }
        int cnt = 0;
        int Index = 0;
        while(cnt < m) {
            while((int)G[Index].size() > k) {
                que.push(G[Index].back());
                G[Index].pop_back();
            }
            while((int)G[Index].size() < k && !que.empty()) {
                int tmp = que.front();
                que.pop();
                G[Index].push_back(tmp);
            }
            if((int)G[Index].size() == k && !vis[Index]) {
                vis[Index] = true;
                ++cnt;
            }
            Index = (Index + 1) % m;
        }
        LL ans = 0;
        for(int i = 0; i < m; ++i) {
            int len = G[i].size();
            for(int j = 0; j < len; ++j) {
                int Index = G[i][j];
                int d = ((i - (num[Index] % m)) % m + m) % m;
                ans += d;
                num[Index] += d;
            }
        }
        printf("%I64d\n", ans);
        for(int i = 1; i <= n; ++i) {
            if(i != 1) {
                printf(" ");
            }
            printf("%d", num[i]);
        }
        printf("\n");
    }
    return 0;
}

E. Reachability from the Capital

题意

在一个 $n$ 个节点、 $m$ 条边的有向图上，问最少要添加多少条有向边，使节点 $s$ 能到达所有节点。

输入

第一行包含三个整数 $n,m,s~(1\leq n\leq 5000,0\leq m\leq5000,1\leq s\leq n)$ ，接下来 $m$ 行每行两个数字 $u_i,v_i~(1\leq u_i,v_i\leq n,u_i\neq v_i)$ ，表示在有向图上有一条从节点 $u_i$ 指向 $v_i$ 的边。

输出

输出要让节点 $s$ 能够到达其他点需要添加的最少的有向边的数量。

样例

输入	输出	提示
9 9 1 1 2 1 3 2 3 1 5 5 6 6 1 1 8 9 8 7 1	3	有向图如图所示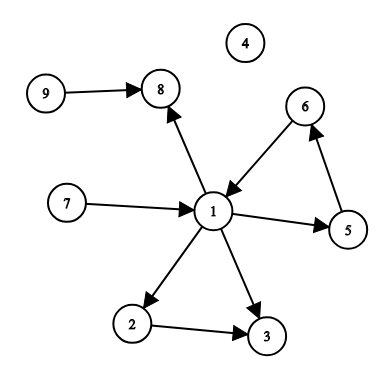：可以添加这三条有向边： $<6,4>,<7,9>,<1,7>$ ，让节点 $1$ 能到达其他所有节点，且 $3$ 是最少需要添加的有向边的数量。
5 4 5 1 2 2 3 3 4 4 1	1	有向图如图所示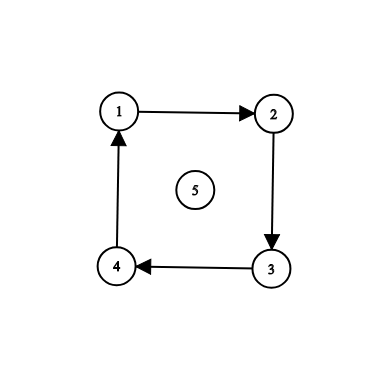：你可以添加 $<5,1>,<5,2>,<5,3>,<5,4>$ 中的任意一条有向边，使 $5$ 能到达其他所有节点。

题解

先对整张图做 $Tarjan$ 缩点，统计新图上入度为 $0$ 且 $belong[s]\neq i$ 的节点数量。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
typedef long long LL;
const int maxn = 5000 + 100;
int n, m, u, v, s, ans;
int top, bcnt, dcnt;
int sta[maxn], dfn[maxn], low[maxn], belong[maxn], deg[maxn];
bool ins[maxn];
vector<int> G[maxn];
void dfs(int x) {
    dfn[x] = low[x] = ++dcnt;
    ins[x] = true;
    sta[top++] = x;
    int len = G[x].size();
    for(int i = 0; i < len; ++i) {
        int pos = G[x][i];
        if(dfn[pos] == 0) {
            dfs(pos);
            low[x] = min(low[x], low[pos]);
        } else if(ins[pos]) {
            low[x] = min(low[x], dfn[pos]);
        }
    }
    if(dfn[x] == low[x]) {
        ++bcnt;
        int pos;
        do {
            pos = sta[--top];
            ins[pos] = false;
            belong[pos] = bcnt;
        } while(pos != x);
    }
}
void Tarjan() {
    bcnt = top = dcnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(ins, 0, sizeof(ins));
    for(int i = 1; i <= n; ++i) {
        if(dfn[i] == 0) {
            dfs(i);
        }
    }
    for(int i = 1; i <= bcnt; ++i) {
        deg[i] = 0;
    }
    for(int i = 1; i <= n; ++i) {
        int len = G[i].size();
        for(int j = 0; j < len; ++j) {
            int pos = G[i][j];
            int u = belong[i];
            int v = belong[pos];
            if(u != v) {
                ++deg[v];
            }
        }
    }
}
int main() {
    #ifdef Dmaxiya
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // Dmaxiya
    ios::sync_with_stdio(false);
    while(scanf("%d%d%d", &n, &m, &s) != EOF) {
        for(int i = 1; i <= n; ++i) {
            G[i].clear();
        }
        for(int i = 0; i < m; ++i) {
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
        }
        Tarjan();
        ans = 0;
        for(int i = 1; i <= bcnt; ++i) {
            if(belong[s] != i && deg[i] == 0) {
                ++ans;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

Codeforces Round #490 (Div. 3)

A. Mishka and Contest

题意

输入

输出

样例

题解

过题代码

B. Reversing Encryption

题意

输入

输出

样例

题解

过题代码

C. Alphabetic Removals

题意

输入

输出

样例

题解

过题代码

D. Equalize the Remainders

题意

输入

输出

样例

题解

过题代码

E. Reachability from the Capital

题意

输入

输出

样例

题解

过题代码

内容目录