@Dmaxiya
2020-12-12T07:23:42.000000Z
字数 4374
阅读 1380
Codeforces Round #444 (Div. 2)
Codeforces
Contests 链接:Codeforces Round #444 (Div. 2)
过题数:3
排名:394/9651
A. Div. 64
题意
对于一个二进制表示的数字,问能否通过删去其中的某些位上的数字,使得最终剩下的数字是一个正的能够整除 的整数。
输入
输入为一个 串 ,表示一个二进制数。
输出
如果可以满足题意,则输出 ,否则输出 。
样例
| 输入 | 输出 | 提示 |
|---|---|---|
| 100010001 | yes | 将后两个 删除之后就是 ,它的十进制数就是 ,因此这个数字可以整除 。 |
| 100 | no |
题解
判断最高位的 后面是否有 个 即可。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <climits>#include <cfloat>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <bitset>#include <algorithm>#include <ctime>#include <functional>#include <iomanip>using namespace std;#define LL long longconst int maxn = 200;char str[maxn];int main() {#ifdef LOCALfreopen("test.txt", "r", stdin);// freopen("out.txt", "w", stdout);#endifios::sync_with_stdio(false);scanf("%s", str);bool flag = false;int cnt = 0;for(int i = 0; str[i]; ++i) {if(str[i] == '1' && !flag) {flag = true;}if(flag && str[i] == '0') {++cnt;}}if(cnt >= 6) {printf("yes\n");} else {printf("no\n");}return 0;}
B. Cubes for Masha
题意
有 个魔方,每个魔方的 个面都写着一个 到 的数字,将魔方摆成一排,按顺序读出这些魔方最上面的数字组成的 位数,问 个魔方最多能够组成 到多大的数字内所有的数。
输入
第一行为一个整数 ,表示魔方的个数,接下去 行每行 个 到 范围内的整数,表示魔方 个面上的数字。
输出
输出一个魔方能够表示的数字的最大连续范围 的上界。
样例
| 输入 | 输出 | 提示 |
|---|---|---|
| 3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 |
87 | 这 个魔方可以组成 到 内的任意一个整数,但是无法组成数字 。 |
| 3 0 1 3 5 6 8 1 2 4 5 7 8 2 3 4 6 7 9 |
98 |
题解
暴力枚举所有组合方式,然后跑一遍找到第一个不能表示的数字。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <climits>#include <cfloat>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <bitset>#include <algorithm>#include <ctime>#include <functional>#include <iomanip>using namespace std;#define LL long longconst int maxn = 1000 + 100;int n;int num[10][maxn], Index[10];bool vis[maxn];void dfs(int depth, int x, int n) {if(depth == n) {vis[x] = true;return ;}for(int i = 0; i < 6; ++i) {dfs(depth + 1, x * 10 + num[Index[depth]][i], n);}}int main() {#ifdef Dmaxiyafreopen("test.txt", "r", stdin);// freopen("out.txt", "w", stdout);#endif //Dmaxiyaios::sync_with_stdio(false);while(scanf("%d", &n) != EOF) {memset(vis, 0, sizeof(vis));for(int i = 0; i < n; ++i) {Index[i] = i;for(int j = 0; j < 6; ++j) {scanf("%d", &num[i][j]);}}do {for(int i = 1; i <= n; ++i) {dfs(0, 0, i);}} while(next_permutation(Index, Index + n));int ans = 1;for(int i = 1; i < maxn; ++i) {if(!vis[i]) {ans = i - 1;break;}}printf("%d\n", ans);}return 0;}
C. Solution for Cube
题意
给定一个 的魔方,问能否通过一次旋转,使得魔方复原。
输入
输入只包含一行 个整数 ,表示魔方 个面每个面的 个数字, 个数字分别表示 种不同的颜色。
输出
如果可以,则输出 ,否则输出 。
样例
| 输入 | 输出 | 提示 |
|---|---|---|
| 2 5 4 6 1 3 6 2 5 5 1 2 3 5 3 1 1 2 4 6 6 4 3 4 | NO | 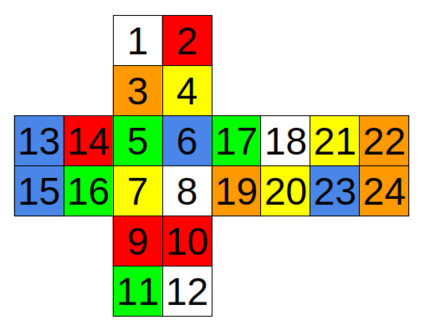 |
| 5 3 5 3 2 5 2 5 6 2 6 2 4 4 4 4 1 1 1 1 6 3 6 3 | YES | 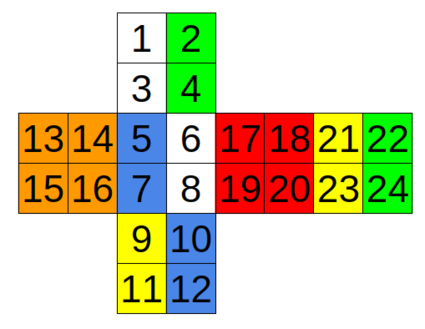 |
题解
这题就是个码农题,把每种旋转方式都写出来就行了。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <climits>#include <cfloat>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <bitset>#include <algorithm>#include <ctime>#include <functional>#include <iomanip>using namespace std;#define LL long longconst int maxn = 100;int a[maxn];int main() {#ifdef LOCALfreopen("test.txt", "r", stdin);// freopen("out.txt", "w", stdout);#endifios::sync_with_stdio(false);bool f = false;for(int i = 1; i <= 24; ++i) {scanf("%d", &a[i]);}if(a[1] == a[6] && a[3] == a[8] && a[5] == a[10] && a[7] == a[12] && a[9] == a[23] && a[11] == a[21] && a[24] == a[2] && a[22] == a[4]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[17 + i] != a[17] || a[13 + i] != a[13]) {flag = false;break;}}if(flag) {f = true;}}if(a[1] == a[23] && a[3] == a[21] && a[5] == a[2] && a[7] == a[4] && a[9] == a[6] && a[11] == a[8] && a[24] == a[10] && a[22] == a[12]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[17 + i] != a[17] || a[13 + i] != a[13]) {flag = false;break;}}if(flag) {f = true;}}if(a[3] == a[15] && a[4] == a[13] && a[17] == a[1] && a[19] == a[2] && a[10] == a[18] && a[9] == a[20] && a[16] == a[12] && a[14] == a[11]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[21 + i] != a[21] || a[5 + i] != a[5]) {flag = false;break;}}if(flag) {f = true;}}if(a[10] == a[15] && a[9] == a[13] && a[16] == a[1] && a[14] == a[2] && a[3] == a[18] && a[4] == a[20] && a[17] == a[12] && a[19] == a[11]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[21 + i] != a[21] || a[5 + i] != a[5]) {flag = false;break;}}if(flag) {f = true;}}if(a[6] == a[20] && a[5] == a[19] && a[14] == a[8] && a[13] == a[7] && a[22] == a[16] && a[21] == a[15] && a[18] == a[24] && a[17] == a[23]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[9 + i] != a[9] || a[1 + i] != a[1]) {flag = false;break;}}if(flag) {f = true;}}if(a[6] == a[16] && a[5] == a[15] && a[14] == a[24] && a[13] == a[23] && a[22] == a[20] && a[21] == a[19] && a[18] == a[8] && a[17] == a[7]) {bool flag = true;for(int i = 0; i < 4; ++i) {if(a[9 + i] != a[9] || a[1 + i] != a[1]) {flag = false;break;}}if(flag) {f = true;}}if(f) {printf("YES\n");} else {printf("NO\n");}return 0;}
